官宣：圆相关概念的考法

朱呈霞

圆是公认的最完美的图形，也是我们初中阶段研究的首个曲线图形。大家对圆了解多少？在小学的时候，我们对圆就有了初步的认识，到了初中，在掌握了三角形、四边形等相关知识的基础上，我们又来学习圆。这里，需要同学们运用所学的知识，化曲为直，解决与圆有关的计算、证明问题。下面，我们就一起来看看中考是如何考查圆的。

例1 （2018·贵州安顺）已知⊙O的直径CD=10cm，AB是⊙O的弦，AB⊥CD，垂足为M，且AB=8cm，则AC的长为（ ）。

A.25cm

B.45cm

C.25cm或45cm

D.25cm或43cm

【解析】先根据题意画出图形。由于点C的位置不能确定，故应分两种情况进行讨论。

解：当C点位置如图1所示时，连接AC、AO。

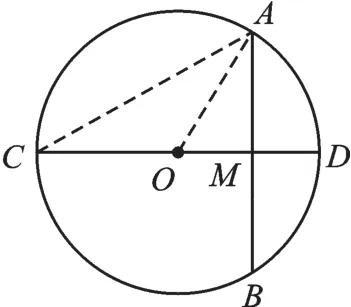
图1

∵⊙O的直径 CD=10cm，AB⊥CD，AB=

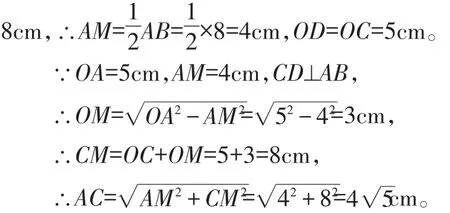
当C点位置如图2所示时，同理可得OM=3cm。

图2

∵OC=5cm，

∴MC=5-3=2cm，

故选：C。

【点评】分类讨论在本章中是解题的重要思想。本题中，对点C在AB的优弧还是劣弧上进行讨论是关键，再构造直角三角形，利用勾股定理来计算。

例2 （2018·甘肃白银）如图3，⊙A过点O（0，0），C（ 3，0），D（0，1），点B是x轴下方⊙A上的一点，连接BO、BD，则∠OBD的度数是（ ）。

A.15° B.30° C.45°D.60°

【解析】连接DC，利用三角函数得出∠DCO=30°，进而利用圆周角定理得出∠DBO=30°即可。

解：如图4，连接DC。

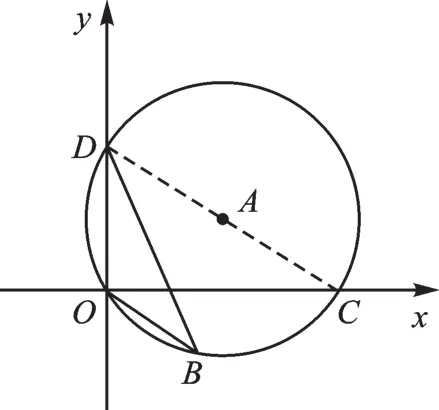
图4

∵∠COD=90°，

∴CD是☉A的直径，

∴OD=1，OC=3，

∴∠DCO=30°，

∴∠OBD=30°。

故选：B。

【点评】本题主要考查圆周角定理，以及利用直角三角形的三边数量关系，求特殊角的度数。

例3 （2018·浙江温州）如图5，D是△ABC的BC边上一点，连接AD，作△ABD的外接圆，将△︵ADC沿直线AD折叠，点C的对应点E落在上。

（1）求证：AE=AB。

图5

【解析】（1）由折叠得出∠AED=∠ACD，AE=AC，结合∠ABD=∠AED，知∠ABD=∠ACD，从而得出AB=AC，据此得证。

（2）作AH⊥BE，由AB=AE且BE=2，知BH=EH=1，根据∠ABE=∠AEB=∠ADB，知cos∠ABE=cos∠ADB，据此得AC=AB=3，利用勾股定理可得答案。

证明：（1）由折叠的性质可知△ADE≌△ADC，

∴∠AED=∠ACD，AE=AC，

∵∠ABD=∠AED，∴∠ABD=∠ACD，

∴AB=AC，∴AE=AB。

解：（2）如图6，过点A作AH⊥BE于点H，

图6

【点评】这道题目考查的知识点比较多，既有全等三角形的性质与判定，又有等腰三角形的判定、勾股定理、锐角三角函数的定义，要求大家要有对所学知识进行转化的能力。总体