探究“圆的切线”中考考点

余旭红

圆的切线的性质定理与判定定理是圆的重要内容，也是各地中考的必考知识。下面结合2018年相关中考试题，归纳与圆的切线有关的考点，以期和同学们共同探讨交流。

考点一 切线的判定定理

切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线。

例1 （2018·湖南邵阳）如图1所示，AB是⊙O的直径，点C为⊙O上一点，过点B作BD⊥CD，垂足为点D，连接BC。BC平分∠ABD。求证：CD为⊙O的切线。

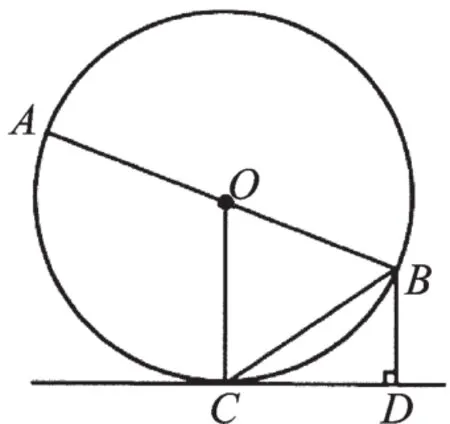
图1

【分析】先利用BC平分∠ABD，得到∠OBC=∠DBC，再证明OC∥BD，从而得到OC⊥CD，然后根据切线的判定定理得到结论。

证明：∵BC平分∠ABD，

∴∠OBC=∠DBC，

∵OB=OC，∴∠OBC=∠OCB，

∴∠OCB=∠DBC，∴OC∥BD，

∵BD⊥CD，

∴OC⊥CD，

∴CD为⊙O的切线。

【点评】从已知条件中可知直线过圆上一个已知点，如果原图中没有连接OC，则需作辅助线：连接已知点和圆心，得到半径，然后证明半径与直线垂直，利用切线判定定理就能说明直线是圆的切线。这种方法简称“连半径，证垂直”。

例2 （2018·贵州安顺）如图2，在△ABC中，AB=AC，O为BC的中点，AC与半圆O相切于点D。

求证：AB是半圆O所在圆的切线。

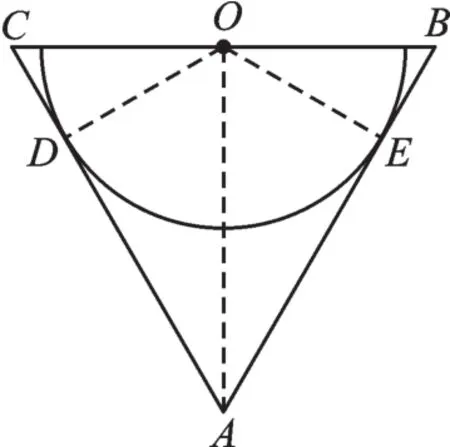
图2

【解析】先判断出∠CAO=∠BAO，进而判断出OD=OE，即可得出结论。

证明：如图2，作OE⊥AB于E，连接OD、OA，

∵AB=AC，点O是BC的中点，

∴∠CAO=∠BAO，

∵AC与半圆O相切于D，

∴OD⊥AC，

∵OE⊥AB，

∴OD=OE，

∵AB经过半圆O的半径的外端点，

∴AB是半圆O所在圆的切线。

【点评】从已知条件中不能判断直线与圆有公共点，辅助线作法是：过圆心作直线的垂线，然后证明垂线段与半径相等，就能说明直线是圆的切线。这种方法简称“作垂直，证半径”。

考点二 切线的性质定理

切线的性质定理：圆的切线垂直于过其切点的半径；经过半径的非圆心一端，并且垂直于这条半径的直线，就是这个圆的一条切线。

例3 （2018·贵州铜仁）如图3，在三角形ABC中，AB=6，AC=BC=5，以BC为直径作⊙O交AB于点D，交AC于点G，直线DF是⊙O的切线，D为切点，交CB的延长线于点E。求证：DF⊥AC。

图3

【解析】如图3，连接OD、CD，根据圆周角定理得∠BDC=90°，由等腰三角形“三线合一”的性质，得D为AB的中点，所以OD是中位线，由三角形中位线性质，得OD∥AC，再根据切线的性质可得结论。

证明：如图3，连接OD、CD，

∵BC是⊙O的直径，∴∠BDC=90°，

∴CD⊥AB，∵AC=BC，∴AD=BD，

∵OB=OC，

∴OD是△ABC的中位线，∴OD∥AC，

∵DF为⊙O的切线，

∴OD⊥DF，∴DF⊥AC。

【点评】此题考查了切线的性质、平行线的判定、三角形中位线性质以及等腰三角形的“三线合一”性质，熟练运用这些性质及定理是解本题的关键。

考点三 切线的判定与性质综合应用

例4 （2018·云南曲靖）如图4，AB为⊙O的直径，点C为⊙O上一点，将弧BC沿直线BC翻折，使弧BC的中点D恰好与圆心O重合，连接OC、CD、BD，过点C的切线与线段BA的延长线交于点P，连接AD，在PB的另一侧作∠MPB=∠ADC。

判断PM与⊙O的位置关系，并说明理由。

图4

【解析】如图4，连接DO并延长，交PM于E，利用折叠的性质得OC=DC，BO=BD，则可判断四边形OBDC为菱形，所以OD⊥BC，△OCD和△OBD都是等边三角形。从而计算出∠COP=∠EOP=60°，接着证明PM∥BC，得到OE⊥PM，再证明OE的长等于⊙O的半径，从而可判定PM是⊙O的切线。解题步骤略。

【点评】此类问题需要同学们熟练掌握切线的判定和性质，并加以灵活应用。

（作者单位：浙江省绍兴市柯桥区钱清镇中学）