基于GOA-SVR的在线英语学习人数预测
崔鹤, 薛媛
(1. 陕西工业职业技术学院 基础部, 咸阳 712000; 2. 西安工程大学 艺术设计学院, 西安 710000)
0 引言
改革开放以来,高等教育得到长足的发展,英语在线网络教学和学习系统在各大高校得到了广泛应用,在管理、学习、评价和监控系统的应用过程中,形成了大量有价值的信息数据,包括学生个人信息、在线学习人数、课程考试成绩、学习时长、学习兴趣点、作业完成情况、学习过程评价等[1]。然而目前这些有价值的数据并未发挥其真实的作用,若能够利用相关学习分析技术和数据挖掘方法发掘出潜在的有价值的规律,有助于英语网络学习流程和管理流程的优化设计,同时可以为英语网络教学提供科学决策的依据。随着在线英语学习人数的大量增加,如何实现英语在线学习人数的准确预测,对网络教学资源的合理配置和利用具有十分重要的意义。
蝗虫优化算法[2](Grasshopper Optimization Algorithm,GOA)是受蝗虫繁衍、聚集、觅食和迁移等行为启发而提出的仿生优化算法,该算法具有收敛速度快、精度高和计算简单等优点,目前被应用于参数优化[3]、特征选择[4]以及振动故障识别[5]等。为提高在线英语学习人数的预测精度,在保证预测值和实际值之间的误差最小化的条件下,针对SVR(Support Vector Regression)模型的预测精度受参数组合C、ε和g的值的选择影响,运用GOA算法优化选取SVR模型的最优参数组合,提出一种基于GOA-SVR的在线英语学习人数预测方法。研究结果表明,GOA-SVR可以有效提高在线英语学习人数预测精度,为在线英语学习人数预测提供了新的方法和途径,从而为在线英语学习资源管理和调度提供了重要的参考依据。
1 蝗虫优化算法
受种群交互力、重力和风力的综合影响,蝗虫个体位置的更新策略如式(1)所示[6]。
Xi=Si+Gi+Ai
(1)
其中,Si为第i个蝗虫受到的与其他蝗虫的交互力的影响;Gi为第i个蝗虫受到的重力影响;Ai为第i个蝗虫受到的风力影响,Xi为蝗虫群体中第i个蝗虫的位置。将环境因素的随机影响考虑进来,式(1)可以修正为式(2)。
Xi=r1Si+r2Gi+r3Ai
(2)
其中,r1、r2、r3三者均为随机数,处于[0 1]之间。交互力影响Si可表示为式(3)。
(3)

(4)

(5)
为实现优化问题的求解,Saremi等提出数学模型为式(6)。

(6)

(7)
式中,cmax=1、cmin=0.000 01;t、T分别为当前迭代次数和最大迭代次数。
2 SVR模型
SVR的核心思想是基于结构风险最小化原则,对于训练样本集{(xi,yi)},i=1,2,…,n,其中,xi表示SVR的输入数据,而yi表示SVR的输出数据,通过定义一个非线性映射函数φ(·)将输入数据集映射到高维特征空间,SVR函数模型定义如式(8)[7]。
f(x)=wTφ(x)+b
(8)
其中,f决定预测值;φ(·)表示非线性映射函数;x表示输入数据向量;w表示权值向量;b表示偏置量。
w和b可求得式(9)。
(9)

SVR致力于求解高维特征空间的最优超平面,使得SVR模型的输入输出数据集之间的整体误差最小。通过二次优化问题求解,权值向量w可表示为式(10)。
(10)

(11)
其中,K(·)表示计算高维特征空间中的两个输入向量内积的核函数。本文核函数选择Gauss函数,其表示为式(12)[9]。
(12)
其中,g表示Gauss核函数宽度。
由于SVR模型的预测精度受参数组合C、ε和g的值的选择影响,在保证预测值和实际值之间的误差最小化的条件下,本文运用GOA算法优化选取SVR模型的最优参数组合。
3 基于GOA-SVR的在线英语学习人数预测
3.1 适应度函数
在保证预测值和实际值之间的误差最小化的条件下,针对SVR模型的预测精度受参数组合C、ε和g的值的选择影响,本文运用GOA算法优化选取SVR模型的最优参数组合,适应度函数选择为:
s.t.C∈[Cmin,Cmax]
ε∈[εmin,εmax]
g∈[gmin,gmax]
(13)
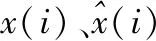
3.2 算法流程
基于GOA-SVR算法的在线英语学习人数预测流程如下:
Step1:GOA算法参数初始化:蝗群的种群规模N、最大迭代次数T、变量维数dim=3以及优化变量的取值范围[LB, UB],本文LB=[0.001;0.001;0.001], UB=[100;10;100];
Step2:随机初始化生成蝗群位置;
Step3:根据目标函数(13)计算蝗群个体的适应度,同时找出当前全局最优解的位置将其作为目标位置;
Step4:根据公式(1)更新搜索个体位置;
Step5:算法终止条件判断。若达到最大迭代次数T,则输出SVR最优参数进行在线英语学习人数预测;反之,返回Step3。
基于GOA-SVR算法的在线英语学习人数预测算法流程如图1所示。

图1 基于GOA-SVR的在线英语学习人数预测算法流程图
4 实证分析
4.1 数据来源
为了验证本文算法的有效性和可行性,选择我国2002年~2017年在线英语学习人数为研究对象,数据如表1所示。

表1 在线英语学习人数
趋势图如图2所示。
将2002年~2012年数据作为训练集,用于建立预测模型,2013年~2017年数据作为测试集,建立模型之后对2018年~2020年在线英语学习人数进行预测。

图2 2002年~2017年在线英语学习人数
4.2 评价指标
为评价在线英语学习人数预测结果,评价指标选择均方根误差(Root Mean Square Error,RMSE)和相关系数R,评价指标公式为式(14)、式(15)[11-12]。
(14)
(15)

4.3 结果分析
GOA算法参数设置:种群规模N=10,最大迭代次数T=100,cmax=1、cmin=0.000 01,GOA-SVR预测结果如图3所示。

图3 GOA-SVR预测结果
为验证GOA-SVR模型的准确性和有效性,将GOA-SVR与GA-SVR、PSO-SVR和SVR进行对比,粒子群算法[13](Particle Swarm Optimization Algorithm,PSO)参数:最大迭代次数T=100,种群规模N=10,学习因子c1=c2=2。遗传算法[14](Genetic Algorithm,GA)算法参数:种群规模N=10,最大迭代次数T=100,交叉概率pc=0.7,变异概率pm=0.1;不同算法在线英语学习人数预测结果对比如图4和表2所示。

图4 在线英语学习人数预测对比图

方法训练样本测试样本RMSERRMSERGOA-SVR0.008 90.995 60.037 30.989 3GA-SVR0.016 20.978 60.039 20.971 1PSO-SVR0.016 80.976 30.045 90.964 2SVR0.017 60.965 20.047 20.945 6
由图4和表2可知:(1) 从整体在线英语学习人数预测结果来看,GOA-SVR的预测结果优于GA-SVR、PSO-SVR和SVR,在训练样本和测试样本上,GOA-SVR的RMSE最小,并且相关系数R达到最大,说明GOA-SVR模型的在线英语学习人数预测值和在线英语学习人数实际值关联程度最高,预测效果最好;(2) GOA-SVR、GA-SVR和PSO-SVR预测精度优于SVR,主要原因在于群智能算法GOA、GA和PSO对SVR模型的参数进行了最优化选择,提高了SVR模型的预测精度。为了给在线学习资源管理和调度提供科学决策的依据,运用GOA-SVR模型对在线英语学习人数2018年~2020年的学习人数进行预测,其预测结果如图5所示。

图5 2018年~2020年在线英语学习人数预测结果
2018年~2020年在线英语学习人数预测结果分别为4 216.33万人、4 321.64万和4 512.86万。
综合分析可知,GOA-SVR可以有效提高在线英语学习人数预测精度,为在线英语学习人数预测提供了新的方法和途径,从而为在线英语学习资源管理和调度提供了重要的参考依据。
5 总结
为提高在线英语学习人数的预测精度,在保证预测值和实际值之间的误差最小化的条件下,针对SVR模型的预测精度受参数组合C、ε和g的值的选择影响,运用GOA算法优化选取SVR模型的最优参数组合,提出一种基于GOA-SVR的在线英语学习人数预测方法。研究结果表明,GOA-SVR可以有效提高在线英语学习人数预测精度,为在线英语学习人数预测提供了新的方法和途径,从而为在线英语学习资源管理和调度提供了重要的参考依据。但是,需要引起注意的是,影响预测结果的调节系数很多,如学习目标、留学政策、学习兴趣、地区差异等。因此,后期需要在本文的研究基础之上,进一步考虑相关影响因素,找到影响在线英语学习人数的核心因素并对其进行量化处理,进一步完善在线学习人数预测模型。

