腕式运动计步器的加速度信号获取与处理
张飞云
(西安交通大学 城市学院, 西安 710018)
0 引言
人有必要通过进行适量运动,来提高身体素质、保持身体健康。但是,其中“适量”一词非常主观。有的人订好了周密的运动计划,但是没有达到计划的运动量就半途而废;有的人热爱运动但忽视了身体的极限。运动过量会对人体产生负担,对人体免疫系统等造成很大损伤[1]。
几十年来,人们越来越关注适量运动对健康的有益影响,计步器等能够将运动量量化显示给用户的设备在海外非常流行。随着健康教育的普及,此类设备在国内逐渐推广。为能时刻了解自身运动状况,一款便捷、高精度的检测设备就非常重要。
早期计步器通过加重的机械开关检测步伐,即以内置的一个平衡锤通过上下往复运动实现一个触电的通/断操作,由计数器记录并展示给用户。这被称作机械式计步器。机械式计步器价格便宜,结构简单,但必须垂直悬挂计步,否则计数偏差较大,现已基本不再使用。
当前较为知名的跨国品牌计步器主要有:日本的卡西欧(Casio)、欧姆龙(Omron)、西铁城(Citizen),美国的安康盟(Acumen)、欧西亚(Oregon)等。国内品牌有绿森林、康都等。除了这些实体检测设备外,随着手机智能化的发展,厂家纷纷开发出各种健身软件,下载即用,非常方便。
很多文献研究过提高计步装置计数准确度的方法,现总结的方法主要分为两大类:一类是基于动态阈值的计步方法,根据采集信号动态调整信号阈值,采集到的数据落在当前信号阈值下方则视为有效步伐并计数[4,5],这是通过正弦波形的减区间判断用户运动进行计步的方法;另一类是基于峰值的计步方法,根据采集信号的斜率查找信号的峰值,再根据采集到的运动加速度波形,分析特征以判断计步[6-8],这是通过正弦波形的拐点处判断步伐进行计步的方法。
另有文献先对采集到信号进行弗里曼编码,然后根据编码内容设计新的计步算法。采用该编码方法的前提是佩戴部位(腰部)受到的干扰不完全随机[9]。但是佩戴在手腕上时,干扰情况却较为复杂。有文献设计了基于陀螺仪的计步器,使用陀螺仪可以增加产品的检测精确度[10],但将基于陀螺仪的计步产品佩戴在手腕上,由于手腕运动角度的多变性,陀螺仪恐怕会对步数检测产生不利影响。
有文献测试出计步器采集的信号波形明显有向下摆动相、向上摆动相、站立相这3个相位的变化,根据这3个相位进行建模,设计算法求解,规定3个相位均被检测到后记录一个有效步伐。本文研究的腕式运动计步器中,实际测试的波形站立相不明显,但有明显的正弦周期,因此本文不按传统的依据以上所述的相位计步编写程序,而是依据实际情况测试中的正弦波变化拟定计步方法。
1 人体运动模型
进行人体运动测量时,相对于其他设备而言,在检测装置中使用三轴加速度传感器,对运动的检测和评估更为准确[12]。可以将用户的运动依据前向、竖向和侧向三个方向进行分解,如图1所示。

图1 人体运动的三个分量
理想情况下,3个方向正好对应设备感应装置的3个轴。但实际应用时感应装置三轴角度未知,因此三轴的测量值是运动加速度在轴上的投影,并非以上声明的分量的真实值。
竖向和前向加速度在一个步行周期(单位步行周期)各阶段的变化。用户行走的每一步,运动的前向和竖向加速度都呈现如下图所示的周期变化,如图2所示。

图2 单位步行周期竖向和前向加速度的变化
用户行走过程中,手臂前后摆动以及迈步动作可以近似成单摆运动,过程中有明显的加速度周期变化的特征。用户行走一步,腿部有蹬地、摆动、触地3个明显的节点,而手臂也有摆动经过最高、最低点、最高点的操作。传感器采集到的速度和加速度都随时间变化。检测的手部(或腿部)摆动运动一般用切向和法向加速度描述,两种加速度对应感应装置的X、Y轴。行走中手臂的摆动过程,如图3所示。
从一个最高点A点运动至另一个最高点E点(或由E至A)的过程。在一个摆动过程中,采集的切向加速度有一个先减后增的过程,相反地,采集到的法向加速度先增后减。接下来分析摆动运动时合加速度的变化。
图3中,θ0是手臂摆动到最高点时与竖直方向的夹角,θ是手臂摆动到B点时与竖直方向的夹角。当手臂从最高点A运动到B点时,切向加速度为式(1)。
at=gsinθ
(1)
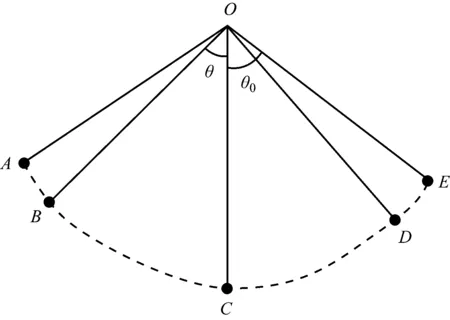
图3 手臂摆动模型
ac=2g(cosθ-cosθ0)
(2)
手臂摆动中某一时刻质点的合加速度即质点法向和切向加速度的矢量和,如式(3)。
(3)
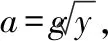
dy=(-6cosθ+8cosθ0)sinθdθ
(4)
当手臂从最高处A点摆到B的时候,有dθ<0、sinθ>0,因此只要判断(-6cosθ+8cosθ0)的正负,即可判断dy,即y的导数的变化情况,也就得出了合加速度a随偏角θ的变化情况。
取θ0=60°,带入上式可得,θ<48°12′时,合加速度增大;θ>48°12′时,合加速度减小。
推广结果到一个完整的摆动过程的各个阶段,如表1所示。
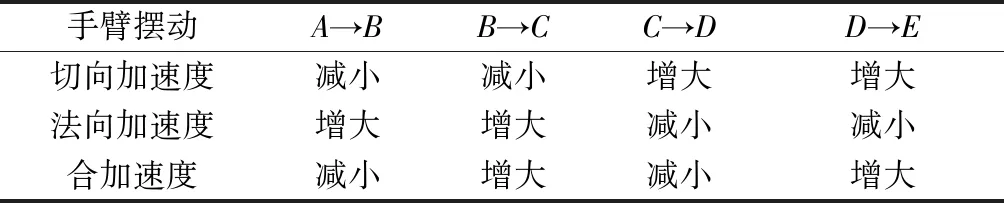
表1 手臂摆动一个周期采集到的加速度变化
从表1中可知,每迈出一步,手臂从一个最高点到另一个最高点(从A到E或从E到A),采集到的合加速度会形成一个完整的正弦波,因此能将计步问题转换成采集到信号的正弦波个数的问题,接下来本文要解决如何应对各种不同的信号,准确的检测采集到的正弦波个数。
3 运动数据采集
加速度数据采集的首要前提是确定合适的采样频率,采样频率过高将会占用过多的内存空间,影响数据处理。而若采样频率较低,采集数据将难以体现人体运动的实际情况,数据误差过大。经过多次试验,决定将采样频率确定为50 Hz,这样能得到较为精确且合理的数据,也便于进行数据处理与分析。选择合适的采样频率解决了手臂摆动一个周期内采样到的加速度变化存在误差的问题。
人体运动数据采集的方法为,在实验者手腕上佩戴采集器,即手腕式计步器,实验者进行行走、上下楼等日常行为活动,在运动过程中,3个轴向的运动数据将由计步器获得,如图4所示。

图4 数据采集
3 三轴数据处理
3.1 单轴数据分析
采样数据图形如图5所示。
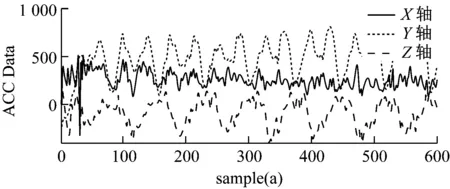
图5 运动16步波形数据
横坐标为在50 Hz的采样频率下, 计步器每经过20 ms所获得的采样点数,纵坐标为计步器所测量的运动加速度的大小。当纵坐标值为512时,表示此时的加速度大小为1g。
实验者行走时,计步器所产生的数据波形图如图6所示。
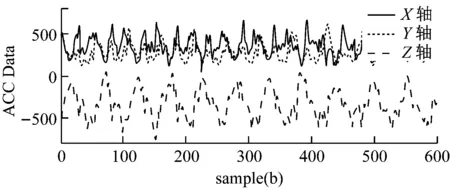
图6 运动21步波形数据
在仅考虑单轴Y轴的情况下,可以得到运动步数。但是在运动时,基于不同时刻的运动状态,在加速度大小产生变化时,有效轴会发生改变,Z轴可能成为有效轴,从而对计步器计数带来较大的影响,造成较大误差。
同样对于图6,在计步过程中,Z轴为运动的有效轴,然而却无法有效地对于运动的步数进行记录。图7也面临同样的问题。
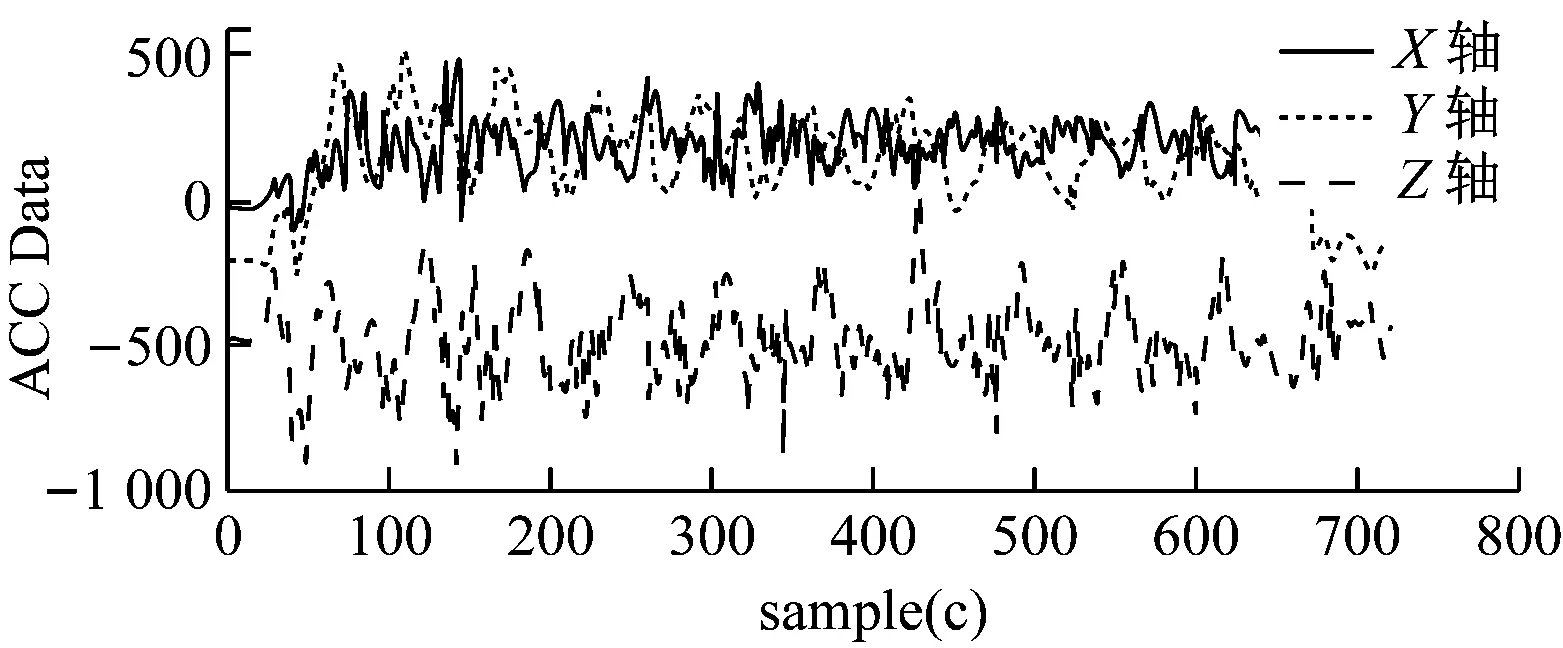
图7 运动20步波形数据
因此,根据以上图形的分析,在三周数据中,仅采用单一轴对于人体运动进行数据处理,具有非常大的误差与局限性,难以获得足够精确与有效的数据处理结果。此外,如果使用单轴对运动进行分析,只能分析单轴方向的加速度,而计步器实际测得的加速度为三轴加速度的综合,因此仅依靠单轴对于运动状态的分析也是不合理的。
3.2 三轴数据处理
对3个轴向的数据综合处理,考虑求解三轴数据的1-范数或2-范数。两种处理方法各有优劣。取1-范数过程较为简单,取绝对值进行求和即可,但数据处理的精度较低。取2-范数,即对三轴数据求取平方和的模,使用MSP430单片机实现这一过程,较为复杂与困难,计算的复杂度较高。因此在数据实际处理的基础上进行下一步分析,如式(5)。
(5)
如图8所示。
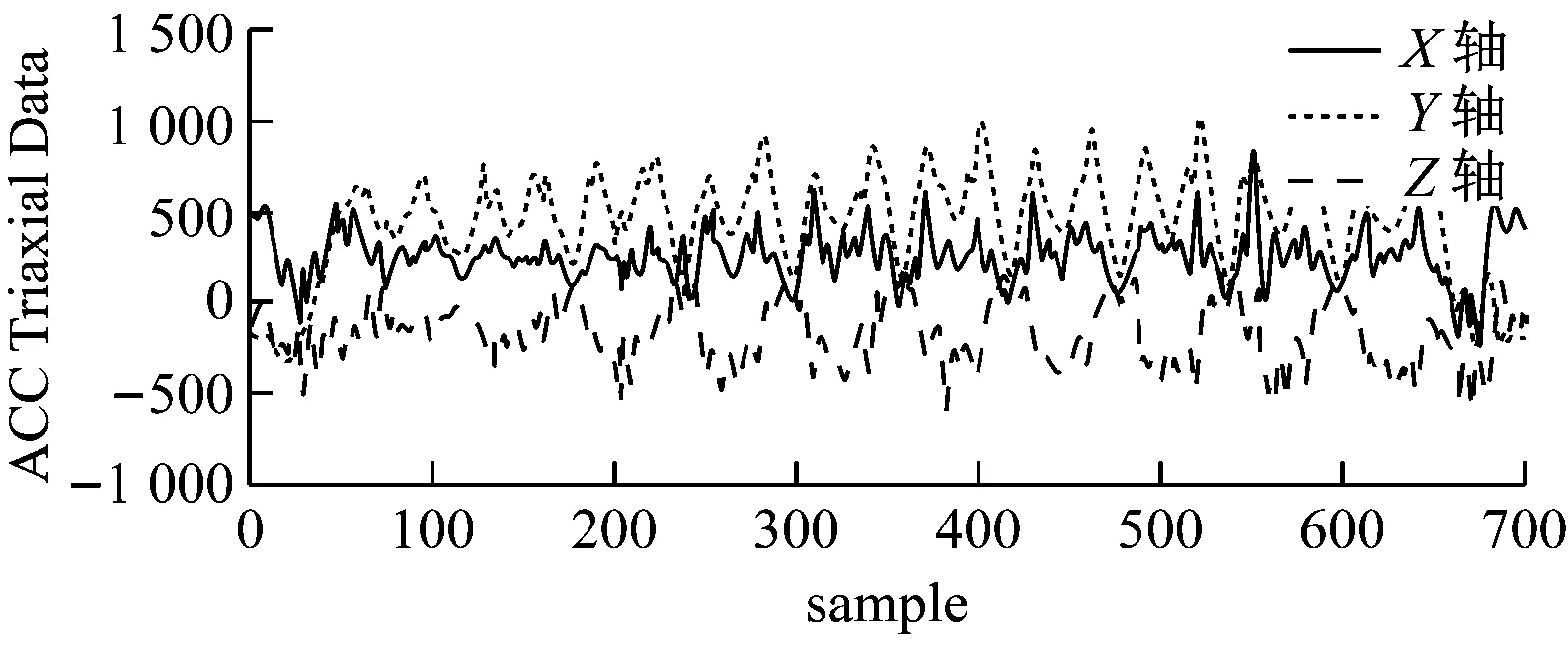
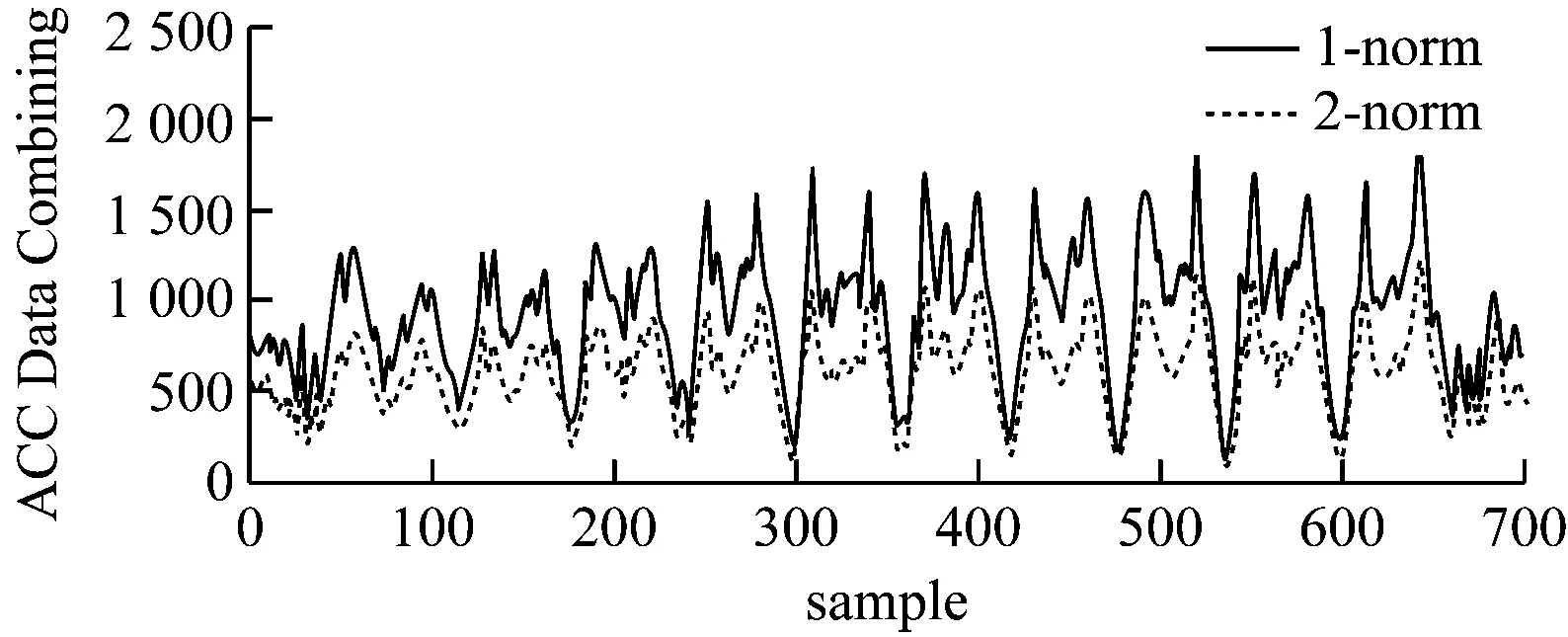
图8 三轴数据及其1-范数和2-范数
由图8可知,1-范数与2-范数的波形变化基本相同,一个正弦波的变化对应测试人员的一个步数。采用2-范数处理数据,其增益较为稳定。但在算法设计中使用自适应阈值时,结果对增益并不敏感,所以无需选用计算复杂度高的2-范数,而1-范数就足以满足算法设计要求。综合考虑,对三轴计步数据采取1-范数的数据处理方法。
4 精确度测试
通过步数采集,反应人体运动量与运动活跃度,无疑计步的精确度是一项重要基础。计步的精确度越高,实验结论就越可靠,也越符合实际运动情况。因此对于计步精确度进行统计分析是至关重要的。实验预期的精确度值为95%,精确度高于95%则认为计步实验是可靠的,否则需要对实验步骤与数据处理进行修正。精确度越高,运动者实际运动的统计越准确越有效;精度越低,运动者实际运动情况统计偏离真实值较远,不具有统计意义和实用价值。精确度的定义如式(6)。

(6)
表2为5名测试人员佩戴手腕计数器进行行走实验的实验数据,从表中的精确度数据可知,4名实验员的计步精确度都是达到了95%的精度要求,精确度的平均值也同样符合要求。同时也存在个别组计步精确度为92.6%,这是由于在计步过程中,不可避免地存在抖动等偶然误差。综合分析,行走计步的实验精确度符合要求。
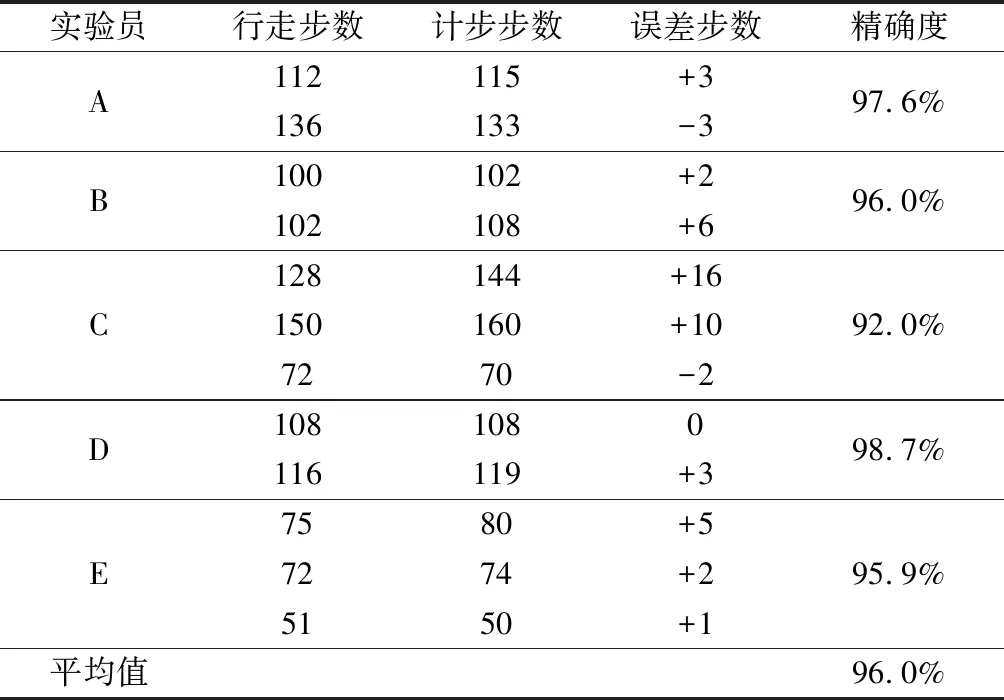
表2 行走测试精确度
表3为4名测试人员跑步实验的实验数据,在跑步测试中,平均实验精确度达到了97.9%,可知跑步实验的精确度略高。这是由于在跑步过程中,步幅与加速度都较大,更利于计步器计步。

表3 跑步测试精确度
表4为上楼实验的实验数据,上楼实验的扰动相对步行与跑步都较大,但平均计步精确度仍能够满足精度要求,为95.8%。
5 总结
文章建立人体运动模型,分析运动时手腕上加速度信号的特点和复杂性。对现有的步数检测方法进行分析和实验测试,根据运动时手腕和身体躯干的周期性加速度变化,以及检测到的加速度波形特征,设计了一套适用于手腕上的步数检测方法,并应用于手腕式计步器设计。最后实验评估结果表明,所设计手腕式计步器的平均计步精确度高于95%,体现出所设计手腕计步器的优势。本文下一步研究旨在给出手腕上步数检测更好的解决方案,进一步实现各种运动形态的精确计步。
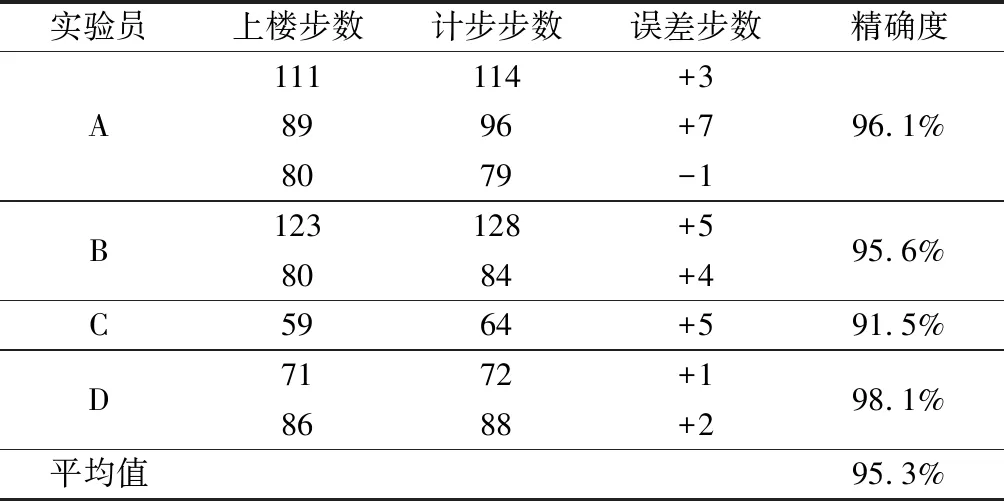
表4 上楼测试精确度

