重叠函数和分组函数的加法与乘法生成子对的相互转化
张廷海, 覃 锋
(江西师范大学 数学与信息科学学院,江西 南昌 330022)
在图像处理[1],决策和偏好建模[2]等应用领域都涉及到分类问题,即根据每个对象的隶属度将其分配到适当的类中。三角模和三角余模作为重要的聚合算子[3]被广泛地应用于其中,然而,在许多情况下,三角模和三角余模所要求的结合性并不满足,于是,Bustince et al.[4]分别在2009年和2012年引入了重叠函数和分组函数这两个特殊的聚合算子,并应用于该领域。
重叠函数可用于图像处理中测度表示对象和背景的两个函数的重叠程度,它是定义在[0,1]×[0,1]上的交换、递增、连续且满足适当的边界条件的二元函数,而分组函数是重叠函数的对偶概念。近几年来,它们在理论和应用上都得到快速的发展,取得了不少成果。2013年Bedregal et al.[5]研究了重叠函数和分组函数的迁移性、齐次性、幂等性和自同构性等重要性质。Jurio et al.[6]讨论了重叠函数和分组函数的一些性质及其在图像阈值分割中的应用。2014年Dimuro et al.[7,8]研究了阿基米德重叠函数的相关性质。2016年乔军胜和胡宝清[9]又给出了利用乘法生成子对来表示重叠函数和分组函数的方法及其相应的性质。大家知道,在三角模和三角余模的表示问题上,通过加法和乘法生成子来表示是两种极其重要的方法,并且两种生成子之间有着紧密的联系,基于这一思想,在本文中我们发现重叠函数和分组函数的加法生成子对与乘法生成子对之间的相互转化关系,并由此获得了这两类函数与其对应生成子对之间的相互关系的新结论,从而为这两类函数的两种生成子对及其相应性质的转换提供了一种有效途径。
1 预备知识
本节将介绍重叠,分组函数的概念及它们之间的联系,并给出一些具体例子。
定义1[4]若二元函数O:[0,1]2→[0,1]满足以下条件:
(O1)O是交换的;
(O2)O(x,y)=0⟺xy=0;
(O3)O(x,y)=1⟺xy=1;
(O4)O是递增的;
(O5)O是连续的;
则称O为重叠函数。
例1重叠函数作为一类合取聚合算子,它与三角模既有交叉又有不同,但重叠函数类比三角模类广泛得多,下面给出一些常见的重叠函数。
(1)任意的无零因子连续三角模;
(2)OmM(x,y)=min {x,y}max {x2,y2};
(4)Op(x,y)=xpyp,p>0;
定义2[5]若二元函数G:[0,1]2→[0,1]满足以下条件:
(G1)G是交换的;
(G2)G(x,y)=0⟺x=y=0;
(G3)G(x,y)=1⟺x=1或y=1;
(G4)G是递增的;
(G5)G是连续的;
则称G为分组函数。
正如三角模与三角余模关于严格(或强)否定具有对偶性,分组函数与重叠函数也关于严格(或强)否定是对偶的。下面给出相关概念和性质。
定义3[5]若连续、严格递减函数N:[0,1]→[0,1]满足N(0)=1,N(1)=0,则称N是严格否定,若进一步对任意x∈[0,1]有N(N(x))=x,则称N是强否定。
命题1[5]设O是重叠函数,G是分组函数,N是严格否定,则
(1)ON(x,y)=N(G(N(x),N(y)))是重叠函数;
(2)GN(x,y)=N(O(N(x),N(y)))是分组函数。
称命题1中的重叠函数ON为G的N对偶重叠函数,分组函数GN为O的N对偶分组函数。特别地,当N是标准模糊否定N(x)=1-x时,称重叠函数ON与分组函数GN分别是G和O的对偶函数。
由命题1可知,给定严格(或强)否定N,由重叠函数可得到对应的对偶分组函数,反之亦然。因此,我们可由N(x)=1-x得到与例1中各重叠函数对偶的分组函数。
例2(1)任意的无1因子连续三角余模;
(2)GmM(x,y)=1-min{1-x,1-y}max{(1-x)2,(1-y)2};
(4)Gp(x,y)=1-(1-x)p(1-y)p,p>0;
2 重叠,分组函数的加法生成子对的概念与有关性质
在重叠函数的表示问题上,DimuroandBedegral[8]在2013年首先引入了重叠函数的加法生成子对的概念,这使得作为二元函数的重叠函数可由两个一元函数和加法运算来表示。
命题2[8]设θ:[0,1]→[0,]和ϑ:[0,]→[0,1]是连续、递减函数,且满足:




则函数Oθ,ϑ:[0,1]2→[0,1],Oθ,ϑ(x,y)=ϑ(θ(x)+θ(y))是重叠函数。
定义4设θ:[0,1]→[0,]和ϑ:[0,]→[0,1]是连续、递减函数,若二元函数Oθ,ϑ:[0,1]2→[0,1],Oθ,ϑ(x,y)=ϑ(θ(x)+θ(y))是重叠函数,则称函数对(θ,ϑ)为重叠函数Oθ,ϑ的加法生成子对,也称Oθ,ϑ是由(θ,ϑ)加法生成的。
我们将看到命题2的结论仅是充分而不必要的,但当(θ,ϑ)是重叠函数Oθ,ϑ的加法生成子对时,函数θ和ϑ的上述条件可相互确定。
定理1设θ:[0,1]→[0,]和ϑ:[0,]→[0,1]是连续、递减函数,且




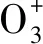

Oθ,ϑ(x,x)=ϑ(θ(x)+θ(x))=ϑ()=0,由重叠函数定义的O2知x=0。

命题3[10]设σ:[0,1]→[0,]和ζ:[0,]→[0,1]是连续、递增函数,且满足:




则函数Gσ,ζ:[0,1]2→[0,1],Gσ,ζ(x,y)=ζ(σ(x)+σ(y))是分组函数。
定义5设σ:[0,1]→[0,]和ζ:[0,]→[0,1]是连续、递增函数,若二元函数Gσ,ζ:[0,1]2→[0,1],Gσ,ζ(x,y)=ζ(σ(x)+σ(y))是分组函数,则称函数对(σ,ζ)为分组函数Gσ,ζ的加法生成子对,也称Gσ,ζ是由(σ,ζ)加法生成的。
类似于重叠函数与分组函数的对偶性,它们的加法生成子对(θ,ϑ)与(σ,ζ)也关于标准否定N(x)=1-x是对偶的。
引理1[10]设θ:[0,1]→[0,]和ϑ:[0,]→[0,1]是满足命题2中条件的连续、递减函数,考虑函数σθ:[0,1]→[0,]和ζϑ:[0,]→[0,1],其中σθ(x)=θ(1-x),
ζϑ(x)=1-ϑ(x),则σθ和ζϑ满足命题3的条件。
由此引理,可以得到类似于定理1的以下结论。
定理2设σ:[0,1]→[0,]和ζ:[0,]→[0,1]是连续、递增函数,且

证明:令θσ(x)=σ(1-x),ϑζ(x)=1-ζ(x),则θσ,ϑζ是连续、递减函数,且由命题1可知二元函数
Oθσ,ϑζ(x,y)=ϑζ(θσ(x)+θσ(y))=1-ζ(σ(1-x)+σ(1-y))=1-Gσ,ζ(1-x,1-y)
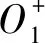
此外,在文[9]中,乔军胜和胡宝清还刻画了重叠函数(分组函数)与其加法生成子对的其它性质。
命题4[9]设θ:[0,1]→[0,]和ϑ:[0,]→[0,1]是连续、递减函数,且


例3考虑两函数θ:[0,1]→[0,],ϑ:[0,]→[0,1],


这些例子说明,命题2只是充分而不必要的,但当ϑ是严格的函数时,命题2就成为下列充分必要的结论。
命题5[9]设θ:[0,1]→[0,]是连续、递减函数,ϑ:[0,]→[0,1]是连续、严格递减函数,则(θ,ϑ)是重叠函数Oθ,ϑ的加法生成子对的充要条件是θ满足ϑ满足
命题6[9]设σ:[0,1]→[0,]和ζ:[0,]→[0,1]是连续、递增函数,且

命题7[9]设σ:[0,1]→[0,]是连续、递增函数,ζ:[0,]→[0,1]是连续、严格递增函数,则(σ,ζ)是分组函数Gσ,ζ的加法生成子对的充要条件是σ满足满足
事实上,对于任意可以利用加法生成子对表示的重叠函数和分组函数,也可以通过两个一元函数和乘法运算来表示,下面给出重叠函数和分组函数的乘法生成子对的概念及与其加法生成子对的联系。
3 重叠函数的乘法生成子对的概念及与其加法生成子对的转化
命题8[9]设g,h:[0,1]→[0,1]是两个连续、递增的函数,且满足:




则函数Og,h:[0,1]2→[0,1],Og,h(x,y)=g(h(x)h(y))是重叠函数。
定义6设g,h:[0,1]→[0,1]是两个连续、递增的函数,若二元函数
Og,h:[0,1]2→[0,1],Og,h(x,y)=g(h(x)h(y))是重叠函数,则称函数对(g,h)为重叠函数Og,h的乘法生成子对,也称Og,h是由(g,h)乘法生成的。
定理3设θ:[0,1]→[0,]和ϑ:[0,]→[0,1]是满足命题2的连续、递减函数,则存在满足命题8的连续、递增函数hθ,gϑ,使得

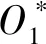

Ogϑ,hθ(x,y)=gϑ(hθ(x)hθ(y))=ϑ(-lnhθ(x)hθ(y))=ϑ(-lne-[θ(x)+θ(y)])=ϑ(θ(x)+θ(y))=Oθ,ϑ(x,y)是重叠函数。
称定理3中的函数对(gϑ,hθ)为由重叠函数的加法生成子对(θ,ϑ)所得的乘法生成子对。
由此定理可知,由重叠函数的加法生成子对(θ,ϑ)经h(x)=e-θ(x)和g(x)=ϑ(-lnx)可得其对应乘法生成子对(g,h)。反之,由重叠函数的乘法生成子对(g,h)经θ(x)=-lnh(x)和ϑ(x)=g(e-x)也可得其对应加法生成子对(θ,ϑ)。
根据定理3,可以得到以下重叠函数的乘法生成子对(g,h)的对应于加法生成子对的下列性质。
命题9设g,h:[0,1]→[0,1]是连续、递增的函数,且Og,h(x,y)=g(h(x)h(y))是重叠函数,则以下结论等价。
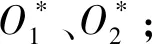

证明:由定理1和定理3立即可得。
命题10设O:[0,1]2→[0,1]是由(g,h)乘法生成的重叠函数,则
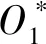
证明:由命题4和定理3立即可得。



定理4设h:[0,1]→[0,1]是连续、递增函数,g:[0,1]→[0,1]是连续、严格递增函数,则以下条件等价
(1)(g,h)是重叠函数Og,h的乘法生成子对;
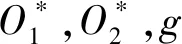
证明:(1)(2)若(g,h)是重叠函数Og,h(x,y)=g(h(x)h(y))的乘法生成子对,则由定理3可知函数θ(x)=-lnh(x)是连续、递减函数,ϑ(x)=g(e-x)是连续、严格递减函数,且(θ,ϑ)加法生成重叠函数Oθ,ϑ(x,y)=Og,h(x,y),再由命题5可知θ满足ϑ满足又由定理3可知,这等价于h满足满足
4 分组函数的乘法生成子对的概念及与其加法生成子对的转化
命题11[9]设s,t:[0,1]→[0,1]是两个连续、递减的函数,且满足:




则函数Gs,t:[0,1]2→[0,1],Gs,t(x,y)=s(t(x)t(y))是分组函数。
定义7设s,t:[0,1]→[0,1]是两个连续、递减的函数,若二元函数
Gs,t:[0,1]2→[0,1],Gs,t(x,y)=s(t(x)t(y))是分组函数,则称函数对(s,t)为分组函数Gs,t的乘法生成子对,也称Gs,t是由(s,t)乘法生成的。
定理5设σ:[0,1]→[0,]和ζ:[0,]→[0,1]是满足命题3的连续、递增函数,则存在满足命题11的连续、递减函数tσ,sζ,使得

证明:类似定理3的证明,只需令tσ(x)=e-σ(x),sζ(x)=ζ(-lnx),x∈[0,1],即可证得。
此定理也说明,分组函数的加法生成子对和乘法生成子对之间也可以相互转化,于是可以得到以下有关分组函数的乘法生成子对的类似于其加法生成子对的性质。
命题12设s,t:[0,1]→[0,1]是连续、递减函数,且Gs,t(x,y)=s(t(x)t(y))是分组函数,则以下结论等价。
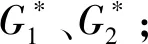

证明:由定理2和定理5即可证得。
命题13设G:[0,1]2→[0,1]是由(s,t)乘法生成的分组函数,则

证明:由命题6和定理5即可证得。



定理6设t:[0,1]→[0,1]是连续、递减函数,s:[0,1]→[0,1]是连续、严格递减函数,则以下条件等价
(1)(s,t)是分组函数Gs,t的乘法生成子对;
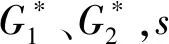
证明:类似于定理4可证得。
由以上关于重叠函数(分组函数)的加法生成子对与乘法生成子对的联系以及重叠函数和分组函数的对偶性,我们可以得到,若(θ,ϑ)是某重叠函数Oθ,ϑ的加法生成子对,则σ(x)=θ(1-x)和ζ(x)=1-ϑ(x)就是其对偶分组函数Gσ,ζ的加法生成子对,g(x)=ϑ(-lnx)和h(x)=e-θ(x)是Oθ,ϑ的乘法生成子对,s(x)=1-ϑ(-lnx)和t(x)=e-θ(1-x)是Gσ,ζ的乘法生成子对,且这四个生成子对可相互确定。


