证题过程不轻言易证——由数学问题2264解答引发的追问
郑步春
(江苏省盐城市教育科学研究院 224002)
细读《数学通报》2015.10期数学问题2264解答过程,其中有一步骤是易证两个三角形全等. 观察这两个三角形,有两组对边相等,要证明其全等,还少一个条件.另一方面,纵观证题过程∠C=2∠B条件就没有引用. 由此引发的追问如下.
1 这题的结论一定不成立吗
取特殊情形. 若∠BAC=90°,此题成为:
已知△ABC,∠A=90°,∠ABC=30°,点D在BC上,点E在线段AD上,∠BED=∠CED=60°.
求证:BD=2DC.

证明过点B作BF∥AC,与AD的延长线交于点F.连接CF,
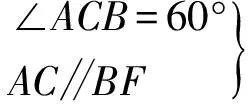


△BFC为等边三角形⟹BF=BC.
又在Rt△ABC中,∠ABC=30°⟹
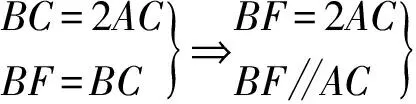
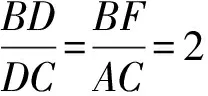
BD=2DC.
由此可见:原题结论是可能成立的.
2 这题的条件∠C=2∠B是多余的吗
调换题目中的条件∠C=2∠B与结论BD=2DC.该题成为:
已知△ABC,点D在BC上,且BD=2DC,点E在线段AD上,∠BED=∠CED=90°-∠ABC.
求证:∠ACB=2∠ABC.
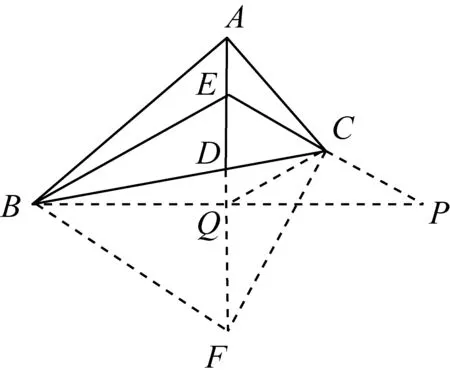
证明过点B作AD的垂线与AD的延长线交于点Q,与EC的延长线交于P.
因为∠BED=∠DEC,BP⊥AQ,
所以Q为BP的中点.
又BD=2DC,
所以D为△EBP的重心,
所以C为EP的中点.
又∠EQP=90°,
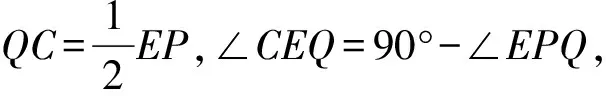
所以∠ECQ=2∠EPQ.
又∠CEQ=90°-∠ABC,
所以∠EPQ=∠ABC,∠ECQ=2∠ABC.
(1)
过点B作直线与AB垂直且与AQ延长线交于点F,连接CF,则
∠CBF=90°-∠ABC=∠CEF,
(2)
所以E,B,F,C四点共圆,
所以∠BCF=∠BEF.
又∠BEF=∠CEF,
所以∠BCF=∠CEF.
(3)
由(2),(3)得∠CBF=∠BCF,
所以BF=FC.
在Rt△ABF中,BQ⊥AF,
所以BF2=FQ·FA,从而FC2=FQ·FA,
所以△CFQ∽△AFC
所以∠QCF=∠FAC.
(4)
又∠CEF=∠ACE+∠EAC,
(5)
∠BCF=∠BCQ+∠QCF,
(6)
综合(3),(4),(5),(6)得∠BCQ=∠ACE.
又 ∠ACB=∠ECD+∠ACE,
∠ECQ=∠ECD+∠BCQ,
所以∠ACB=∠ECQ.
(7)
由(1),(7)得∠ACB=2∠ABC.
由此可见:条件∠C=2∠B是结论BD=2DC成立的必要条件. 原证题过程中∠C=2∠B没用引用,表明原证题是有问题的.
3 这题的结论一定成立吗
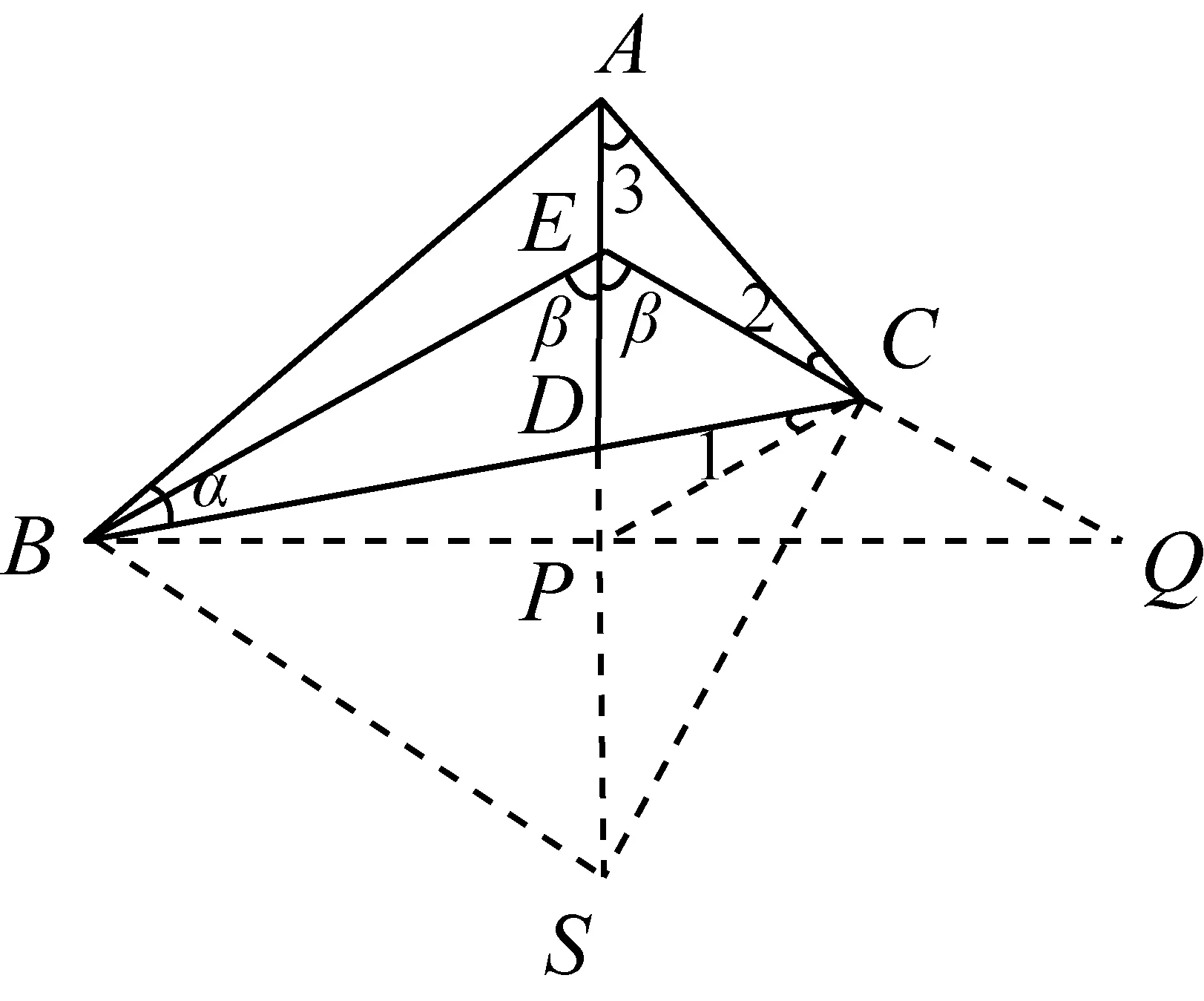
已知△ABC,点D在BC上,且∠ACB=2∠ABC.点E在线段AD上,∠BED=∠CED=90°-∠ABC.
求证:BD=2DC.
分析根据已知条件∠BED=∠DEC,过点B作AD所在直线的垂线,与AD的延长线交于点P,与EC的延长线交于点Q.从而构造了等腰△EBQ,P为BQ的中点. 因此,结论BD=2DC成立,与D是△EBQ的重心是等价的. 相应地,只要证明点C为EQ的中点,又∠APQ=90°,即只要证明PC=CE.
设∠DEC=β,∠ABC=α,则∠ACB=2α,α+β=90°,为此,只要证明∠EPC=∠CEP=β,即只要证明∠ECP=2α. 如图示,即证∠1=∠2.
又∠2+∠3=β.以CB为边,作∠BCS=β,与AP延长线交于S,连BS.
由∠BCS=∠BED=β知B,S,C,E四点共圆,所以∠CBS=∠CES=β.相应地,SB=SC.
又∠ABC=α,α+β=90°,所以∠ABS=90°,从而SB2=SP·SA,即
SC2=SP·SA,所以△SPC∽△SCA, 因此,∠PCS=∠CAS=∠3.
从而∠1+∠3=∠BCP+∠PCS=∠BCS=β,所以∠1=∠2.
综上分析,这题的结论是成立的.
4 原证题过程错在哪个环节
正如本文开头所述,错在易证△BQC≌△PQC.结合原证题过程,在此环节可改证:
∠CFB=180°-∠BEC
=180°-2∠BEF
=180°-2(90°-∠ABC)
=2∠ABC
=∠ACB.
所以AC为四边形BFCE外接圆的切线. 从而∠PCF=∠CBF=∠BCF.即原证题过程中所要的结论∠BCQ=∠PCQ.

