微型扬声器摆动模态对其辐射声场的影响∗

毛燕蓉 沈 勇

(南京大学声学研究所 近代声学教育部重点实验室 南京 210093)

0 引言

近年来，随着智能手机、笔记本电脑、可穿戴设备等移动终端的兴起与普及，微型扬声器单元的应用越来越广泛，人们对微型扬声器单元音质的要求也越来越高。因此，对微型扬声器单元性能的研究与优化逐渐成为行业的研究热点[1−4]。这些研究大多集中于对微型扬声器单元设计参数、造型等进行优化，来提升微型扬声器单元的声学性能。然而，这些研究大多假设微型扬声器单元振动系统只存在一维纵向振动(即振动方向垂直于振膜面)，而忽略了微型扬声器单元的摆动模态对其性能的影响。

在中低频段，常规的动圈式扬声器单元在对称力的作用下仅产生沿球顶法向的位移且振膜各处位移相同，可以看作活塞运动。但是扬声器在生产和使用过程中通常出现大量不对称现象，如质量分布不均匀，折环顺性不对称，侧出声情况下声负载不对称等，此时扬声器单元由于受力不平衡，会出现不理想的摇摆振动，产生明显的摆动模态。不同于普通扬声器，由于缺少定位支片，在微型化、高声输出的发展趋势下，微型扬声器单元的摆动模态尤其突出，如图1所示。

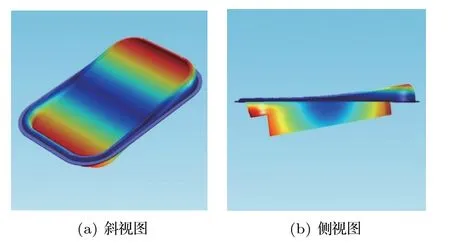
图1 微型扬声器单元摆动模态(绕短轴方向摆动)Fig.1 Rocking modes in micro speakers (Short axis direction)

Bright 等[5]用实验的方法证明了摆动模态的存在，提出产生摆动模态的关键在于质量、顺性或磁场分布等的不对称，并建立理论模型，用模态分析的方法对不对称顺性造成的摆动模态进行分析。Klippel 等[6−7]在模态分析的基础上，将摆动模态下的振膜运动分解为摆动与平动两部分，并通过模态分析预测振膜表面上造成摆动模态的位置和原因。Cardenas 等[8]通过有限元模型对摆动模态进行模拟并分析其根因。

然而，上述研究大多集中在对扬声器单元摆动模态产生根源的探究及其测试方法，而摆动模态对其辐射声场的影响却少有提及。由于移动终端所使用的微型扬声器单元绝大多数为电动式矩形扬声器，故本文针对一款具有摆动模态的矩形微型扬声器单元(绕短轴方向摆动，如图1所示)，利用激光传感器采集摆动模态下微型扬声器单元振膜的振动位移，通过理论计算，从辐射声压级、指向性与平面声场等角度探究矩形微型扬声器单元摆动模态对其辐射声场的影响。经过研究发现，除了会造成微型扬声器单元擦圈打底等机械性缺陷，摆动模态还会造成微型扬声器单元频响凹陷、中低频存在指向性等现象，对其辐射声场产生明显的影响。

1 微型扬声器单元辐射声场的测量与计算

通用的声场测量方法需利用传声器对声场中各点进行声压采集，一般而言，较大范围的声场测量均极为耗时。此外，为获得准确的声场信息，对各测量点的位置定位也要求较高。因此，为快速获得微型扬声器单元的辐射声场，本文利用激光传感器采集振膜的振动位移对辐射声场进行理论计算，从而避免繁杂的声场测量过程。

1.1 微型扬声器单元振动位移采集

如图2所示测量系统，安装于可移动导轨上的激光传感器采集微型扬声器单元振膜的振动位移，位置控制器利用导轨控制激光传感器对振膜各点位移进行拾取。同步记录测试点位置信息与振膜振动位移信息，即可对整个微型扬声器单元振膜的振动进行采集。

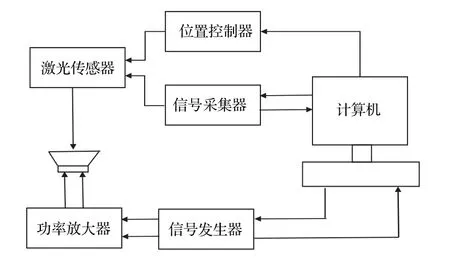
图2 微型扬声器单元位移采集系统示意图Fig.2 Schematic diagram of displacement acquisition system for micro speaker unit

图3给出实测的一款存在摆动模态的微型扬声器单元振膜上三个不同位置(振膜中心点及两条短边中点)的位移幅值与相位响应曲线。由图3可以看出，不同于正常微型扬声器单元的活塞振动情况，具有摆动模态的微型扬声器单元振膜上各点位移的幅值与相位差异明显，特别在摆动频率点附近(本文研究单元摆动频点为f= 1100 Hz，此处摆动最为剧烈)，部分位置点相位差大于90◦，存在明显的反向振动情况。图中1 点为振膜中心点，2、3 分别为两边短轴的中点。

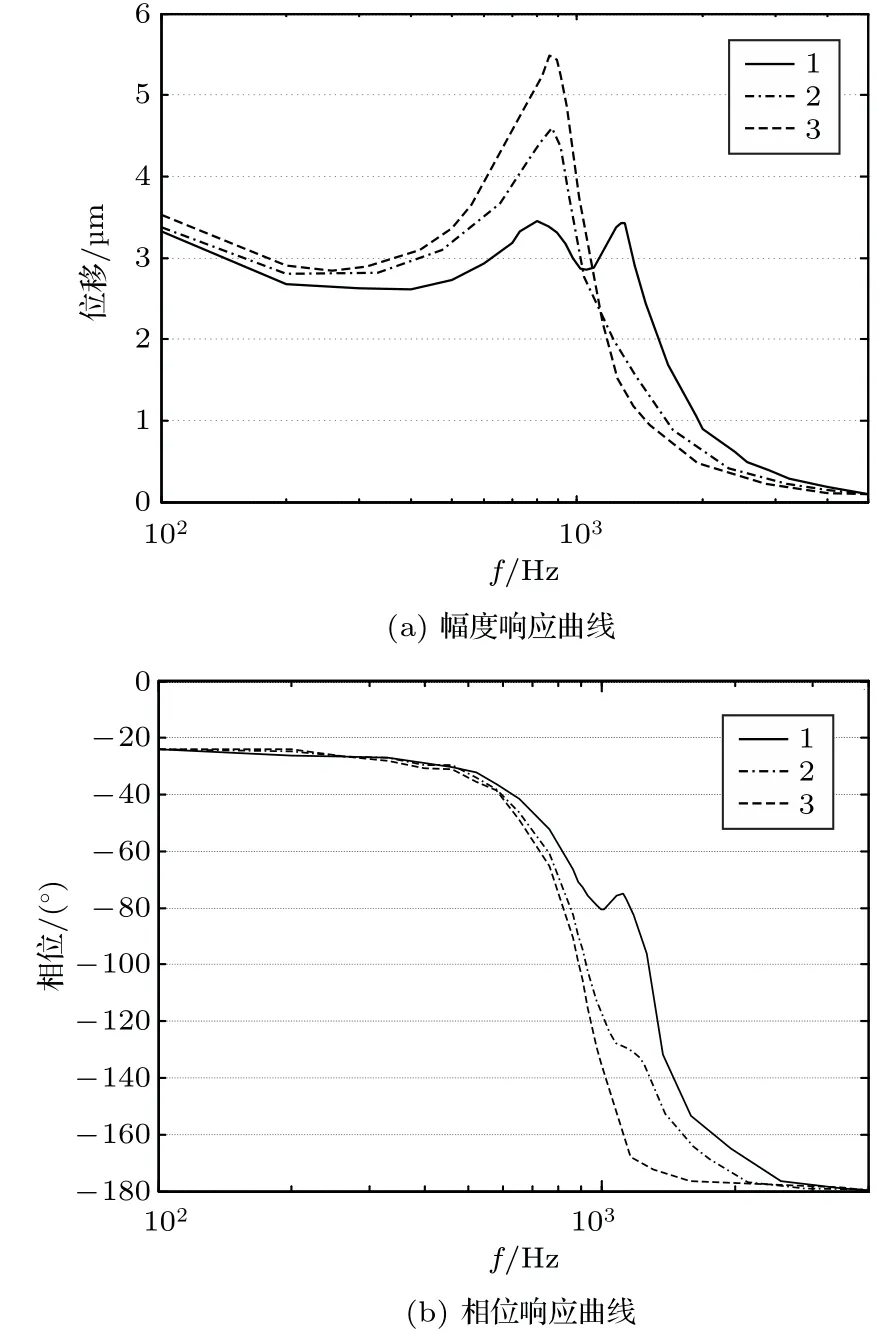
图3 具有摆动模态的微型扬声器单元振膜上不同位置的位移响应曲线Fig.3 Displacement response curves of micro speaker with different position of rocking modes

1.2 微型扬声器单元辐射声场的理论计算与实验验证

一般而言，微型扬声器单元需安装于障板上进行声学测量，为方便说明，规定微型扬声器单元振膜面为x-z平面，其中短轴为z轴，振膜中心与坐标系原点重合，如图4(a)所示，后续章节均采用此坐标系，不再赘述。对于一般的微型扬声器单元，由于在中低频段振膜上各点振动位移基本一致，因此其振动可以等效为刚性活塞运动，其辐射声压可由式(1)计算[9]。

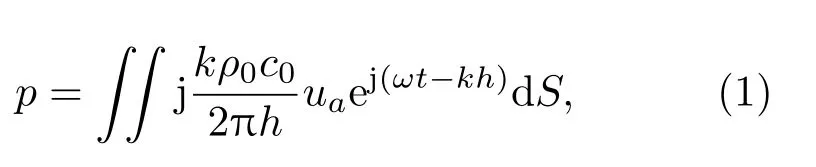
其中，ρ0为空气密度，c0为空气中声速，ua为速度复振幅，h为振膜各点与声压采集点S的距离。

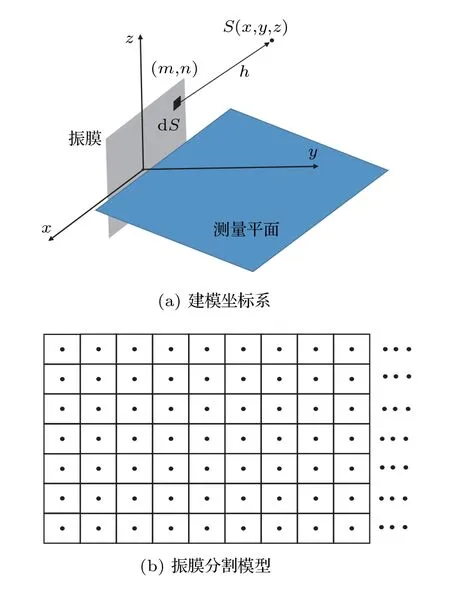
图4 微型扬声器单元辐射模型Fig.4 Radiation model of micro speaker

然而在摆动模态下，微型扬声器单元振膜上各点振动位移的大小与相位均不相同，不能再对整体使用式(1)。将振膜平面分割为若干个小矩形面元，如图4(b)所示，本文根据振膜大小划分成7×9 个矩形面元，以每个面元中心点(m,n)的振动位移作为整个面元的振动位移，则面元dS在空间中任一观测点S(x,y,z)处产生声压为

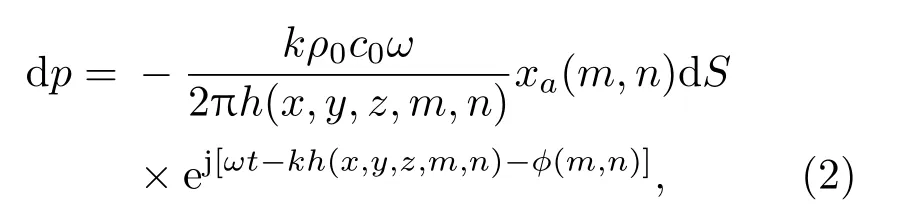
式(2)中，xa(m,n)为面元位移的幅度函数，ϕ(m,n)为面元位移的相位函数。面元与观测点之间距离则观测点处总声压可通过对振膜面积进行积分获得，为

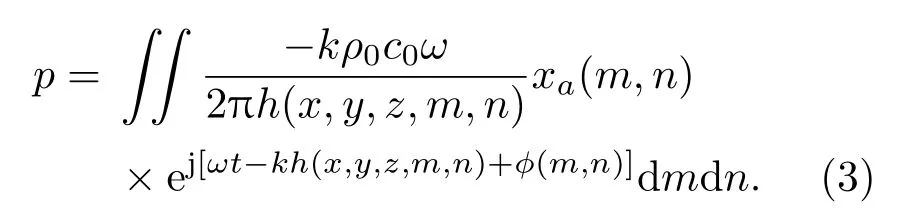
对式(3)进行离散化，则观测点声压p为

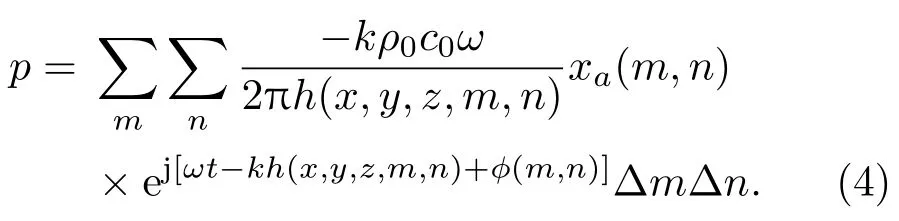
为验证上述理论计算的准确性，针对一普通微型扬声器单元(产品规格1511，后续均采用此款单元，不再赘述)，不失一般性地随机选取声场中任意三点(本文选取的三点分别为(−7,−2,5)，(6,4,2)，(0,1,4)，单位为cm)进行声压测试并与理论计算进行对比。图5给出实测频响曲线与计算频响曲线的对比。由图5可以看出，采用本节所述方法进行的微型扬声器单元辐射声场的理论计算与实测吻合良好，理论符合实际。

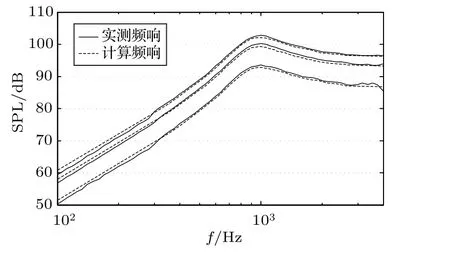
图5 微型扬声器单元频响曲线的理论计算与实测对比Fig.5 Theoretical calculation and measurement comparison of frequency response curves for micro speaker

2 微型扬声器单元摆动模态对其辐射声场的影响

为探究摆动模态对微型扬声器单元辐射声场的影响，本节选择一款存在摆动的微型扬声器单元(绕短轴摆动，摆动主要由折环顺性不同引起，见图1进行说明，并利用一无明显摆动的同款微型扬声器单元作为对比。对于其他摆动方向，原理相同，本文不作赘述。利用第1 节所述位移测量与声场计算方法，对其辐射声场进行探究。

2.1 摆动模态对微型扬声器单元频率响应的影响

声压级频率响应SPL(f)是评价微型扬声器单元声学性能的重要指标[10]，一般选取振膜正前方10 cm 作为测试点。由式(4)可知，微型扬声器单元声压频率响应SPL(f)为

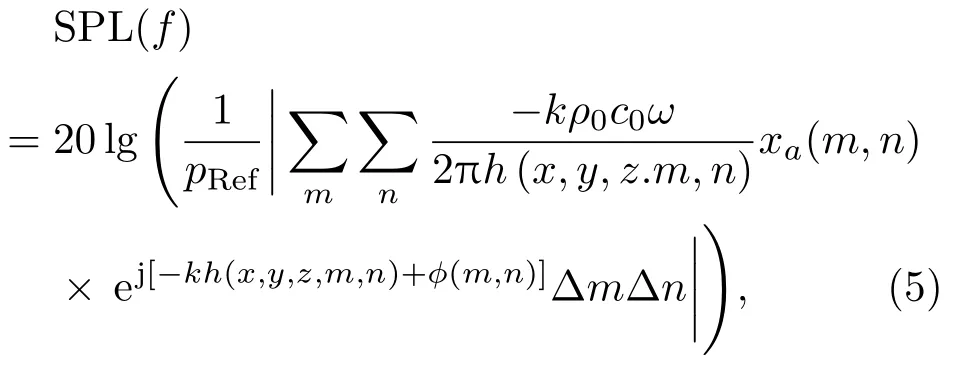
式(5)中，pRef= 2×10−5Pa 为参考声压。根据测量位移和式(5)分别计算并作出绕短轴摆动的微型扬声器单元与正常微型扬声器单元的声压频率响应进行对比，如图6所示(具有摆动的微型扬声器单元实测频响曲线同步绘于图中)。

图6 具有摆动模态的微型扬声器单元与无摆动模态的微型扬声器单元的频率响应曲线对比Fig.6 Comparison of frequency response curves between micro speaker with rocking modes and without rocking modes

从图6可以看出，由于摆动模态，存在摆动的微型扬声器单元的声压级频率响应在相应的摆动频点附近存在明显的凹谷，与正常微型扬声器单元频响相比差异明显。而在非摆动频点附近，除了由于顺性不同导致的频响上升段差异外，二者频率响应无明显不同。这是由于摆动模态下振膜上各点位移的大小和相位各不相同，在声压采集点处产生“声抵消”现象，造成声压级频率响应凹陷。因此可以得出结论：由于摆动模态的存在，造成微型扬声器单元声压级频率响应在摆动频点附近存在异常凹谷，影响微型扬声器单元的频率响应。

2.2 摆动模态对微型扬声器单元辐射指向性的影响

辐射指向性描述了声源辐射随方向而异的相关特性，为任意方向角θ方向的声压幅值与θ= 0◦轴上的声压幅值之比[9]，即D(θ) = (pa)θ/(pa)θ=0。一般而言，由于微型扬声器单元尺寸较小，在中低频段可以视为点源，因此不存在明显指向性。然而由于摆动模态的存在，上述结论不再成立。为探究摆动模态对微型扬声器单元辐射指向性的影响，分别计算微型扬声器单元在图4(a)所示的y-x平面与y-z平面上的辐射声场与指向特性，讨论摆动模态对垂直于摆动轴、平行于摆动轴这两个方向的辐射指向性的影响。

图7对比了存在摆动的微型扬声器单元与正常微型扬声器单元在垂直于摆动轴平面(y-x平面)上的辐射声场与辐射指向性。由图7(a)、图7(c)可以看出，在摆动频率点上，不同于正常微型扬声器单元在平面声场上类似于点源辐射的情况，存在摆动的微型扬声器单元平面声场明显向一侧偏移。与此同时，由图7(b)、图7(d)对比二者指向性图也可以说明同样现象：正常微型扬声器单元指向性图基本为圆形，说明其无指向性。而存在摆动的微型扬声器单元在摆动频点上则存在明显的指向性。由图7(e)、图7(f)可以看出，在非摆动频率点上，存在摆动的微型扬声器单元也不存在指向性。

在平行于摆动轴的平面(y-z平面)上，存在摆动的微型扬声器单元的辐射声场与辐射指向性如图8所示。由图8可以看出，此时微型扬声器单元在此方向上也无明显指向性。

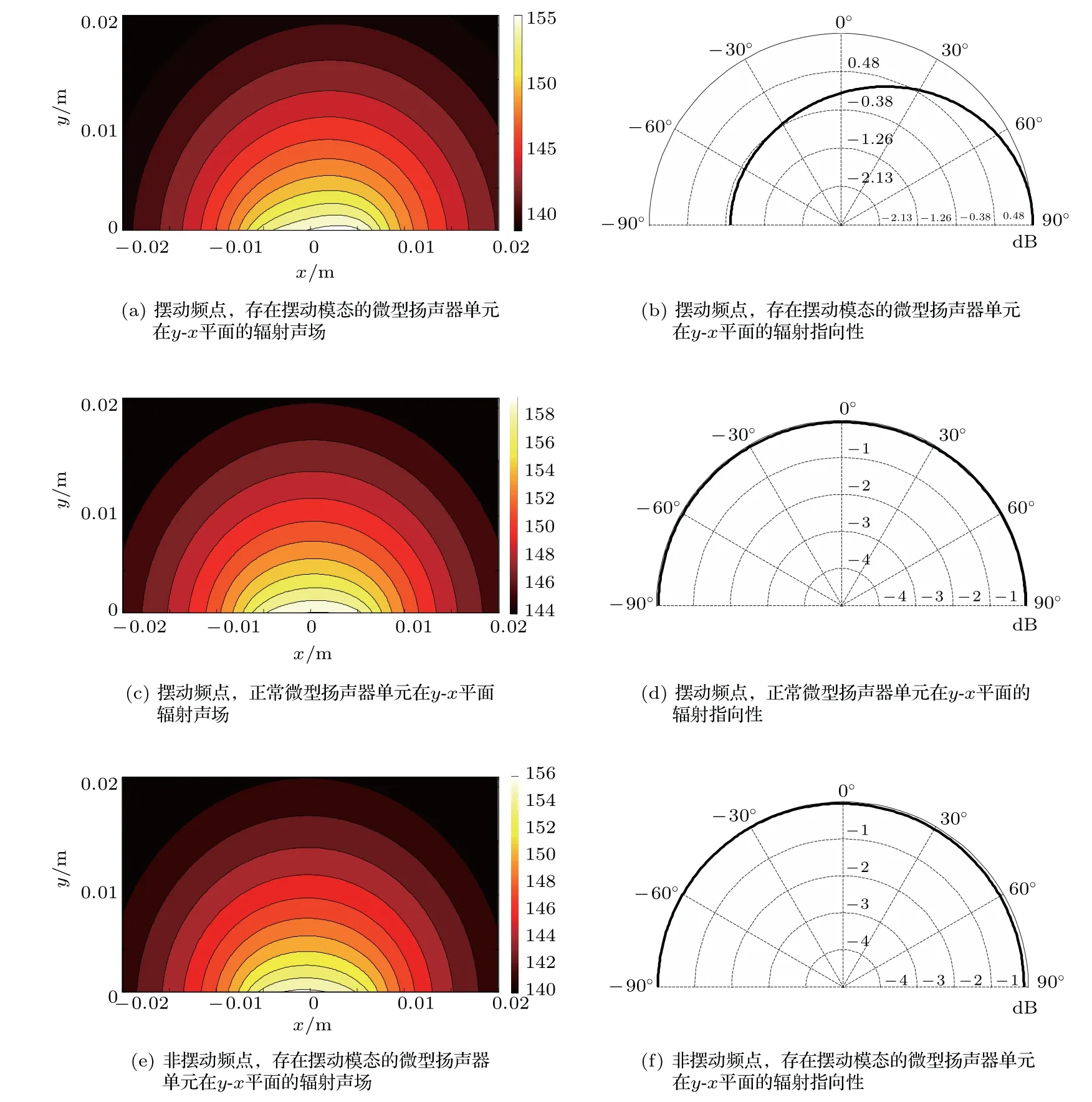
图7 微型扬声器单元在y-x 平面的辐射声场与指向性对比Fig.7 Comparison of radiation sound field and directivity of micro speaker in y-x plane

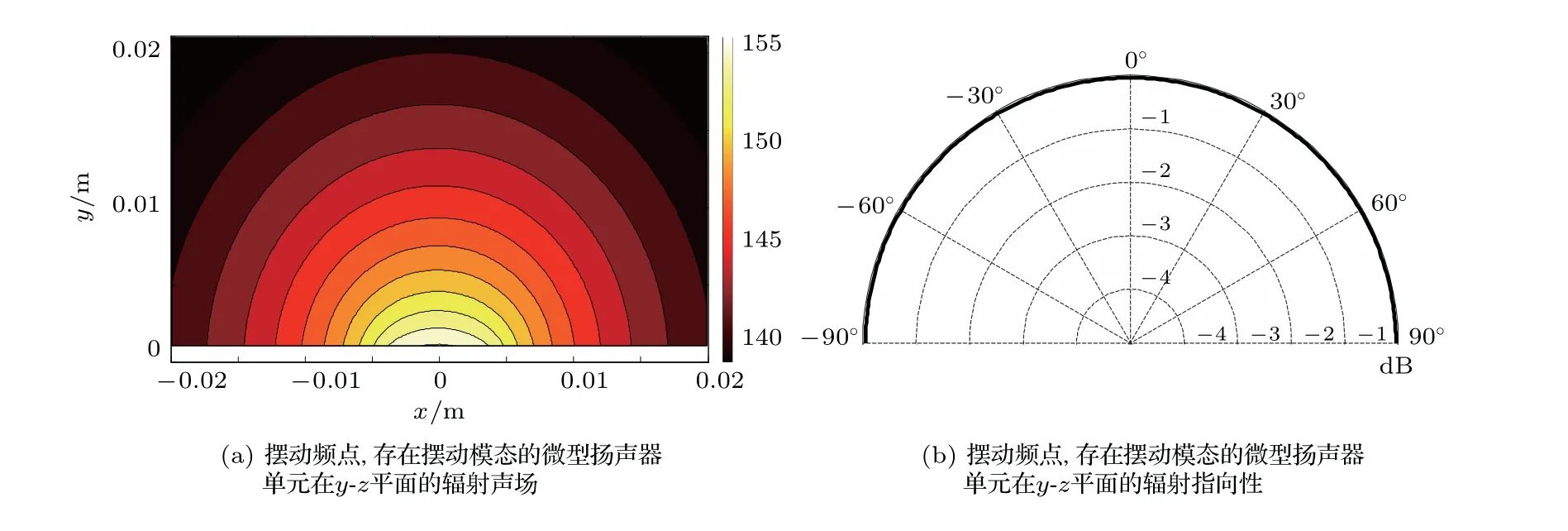
图8 微型扬声器单元平面辐射声场与指向性对比Fig.8 Comparison of planar radiated sound field and directivity of micro speaker

因此，通过上述分析，可以得出结论：摆动模态能够显著影响微型扬声器单元的辐射声场与辐射指向性，造成微型扬声器单元产生中低频指向性。由于摆动模态的存在，在对应的摆动频点上，微型扬声器单元在垂直于摆动轴的平面上存在明显的指向性，y-z平面声场发生明显的偏移。而在非摆动频点，在平行于摆动轴平面(y-z平面)上，微型扬声器单元指向性未发生明显变化。

3 结论

伴随着微型扬声器单元微型化、纤薄化、高声输出的发展趋势，摆动模态对微型扬声器单元的影响越发受到业界的关注。当前，关于摆动模态的研究大多集中在对摆动模态产生根源的探究及其测试方法，而摆动模态对微型扬声器单元声学性能的影响却少有涉及。

本文利用激光传感器采集摆动模态下微型扬声器单元的振动位移，通过测试发现，存在摆动的微型扬声器单元在摆动频率点附近不再表现为整体活塞振动，振膜上各点位移的幅值与相位差异明显。

在准确获得微型扬声器单元振动位移的基础上，本文基于理论计算，从辐射声压级、辐射指向性与平面声场等角度探究微型扬声器单元摆动模态对其辐射声场的影响。通过研究发现，摆动模态会造成微型扬声器单元出现异常的频响凹陷。此外，由于摆动模态的存在，微型扬声器单元在垂直于摆动轴平面上出现中低频指向性等现象，对其辐射声场产生显著影响。在实际的微型扬声器单元开发过程中，可以根据频响是否存在异常凹谷来判断微型扬声器单元受摆动模态影响与否，并根据其中低频辐射指向性来判断摆动模态的摆动方向，由此可以进一步定位其产生根因并加以改善。