HDP-HSMM的磨削声发射砂轮钝化状态识别∗

钟利民 李丽娟 杨 京 梁 彬 程建春 刘翔雄

(1 南京大学声学研究所 南京 210093)

(2 人工微结构科学与技术协同创新中心 南京 210093)

(3 华辰精密装备(昆山)股份有限公司 昆山 215337)

0 引言

磨削加工是一种精密的切削加工技术，与其他切削加工相比较，具有加工速度快、加工精度高等特点。在磨削加工过程中，刀具即磨削砂轮磨粒必然会发生磨损现象，使得切削力增大，切削温度增高，切削震颤现象产生。这不仅会影响加工效率，还会使得加工精度变差，工件表面粗糙度上升。通常情况下，砂轮的钝化由经验丰富的工人凭经验判断，不仅浪费人力而且效率低下。为了实现生产的自动化，工程师们提出了各种智能化的砂轮钝化状态检测方法。一般可分为直接法和间接法两大类[1]。直接法利用光学传感器直接观察砂轮的状态[1]，但这种方法仍需先停止加工过程，不能提高生产效率。间接法利用加工过程中产生的压力、热量、振动、温度、声发射(Acoustic emission, AE)信号等物理参数的变化间接判断砂轮的状态。这将方便快捷地对加工工件的状态实现监控且并不需要停止加工过程，大大提高了生产效率。

AE 是指材料在外压或载荷作用下产生塑性变形，从而产生辐射弹性波的现象，即材料结构变化引起的能量释放过程，因此，AE 现象也叫应力波发射。随着传感器技术的发展以及生产实践中自动化水平的提高，通过材料内部结构变化或材料表面裂纹扩展所引起的应力波来判断材料损伤以及机械故障的无损检测方法得到了大力发展[2−3]。相较于其他无损检测方法，AE 检测方法由于具有不受被检构件几何结构限制且对检测环境要求低等优点，更加适用于生产环境恶劣、结构复杂的大型机械的整体检测，在航天航空、船舶工业、桥梁土建等大型工程项目的结构检测中得到了广泛应用[2−3]。近年来，在利用磨削声来检测刀具状态方面已做出了很多工作。Kurada 等[1]通过对原始AE 信号进行傅里叶分析，由频谱图来判断刀具状态；Mokbel等[2]证实刀具的磨损随着AE信号幅值的增大而越来越严重；Lezanski 等[4]通过提取AE 信号特征并输入神经网络来监控工件的状况；Hosokawa 等[5]和Kwak 等[6]利用小波变换得到AE 信号在时频域的变化来判断刀具和工件状态；文献[7-10]通过提取AE 信号特征并使用模式识别技术来监测刀具钝化状态。以上方法虽然能够检测加工过程中砂轮的状态，但并没有对砂轮钝化程度进行细分。不同钝化程度的砂轮具有不同的加工精度。在工件的加工精度和质量要求比较高时，轻微钝化的砂轮可能就会导致工件不合格。因此，在高精度加工时，需要对砂轮的钝化程度进行量化分级，以便及时更换符合要求的砂轮。

本文提出了一种基于分层Dirichlet 过程-隐半马尔科夫模型(Hierarchical Dirichlet processeshidden semi Markov models, HDP-HSMM)的砂轮钝化状态磨削声检测方法。该方法不需要先验的砂轮钝化状态知识，而是通过对采集到的AE 信号自动聚类实现对砂轮钝化程度的有效划分，进而得到整个加工过程中砂轮所处的状态。首先，将经过小波阈值去噪后的AE 信号分割成多个有重叠的帧。然后，提取每一帧中的8 维AE 信号特征，组成AE 数据集。最后，使用这些AE 数据集训练HDP-HSMM，得到砂轮状态序列。并用测试数据集对训练好的模型进行测试。其结果表明，上述方法能够准确识别砂轮的不同钝化状态，有极重要的工业应用价值。

1 HDP-HSMM砂轮钝化状态识别方法

在高精度磨削加工时，砂轮的不同钝化状态具有不同的加工精度。磨削过程中发出的AE 信号可作为对砂轮不同钝化状态判断的依据。磨削加工过程中的AE 信号主要由被加工工件的塑性形变、碎屑脱落、砂轮磨粒脱落以及碎屑和砂轮的摩擦等因素所引起[11]。此外，材料内部缺陷在局部应力作用下出现滑移、位错、开裂并发出弹性波的现象也是磨削AE 的来源之一[11−12]。工件的塑性变形是AE 信号的主要来源，其发出的弹性波频带分布在100 kHz∼300 kHz 之间，切削液和砂轮堵塞引起的噪声主要分布在100 kHz 以下，电噪声频率一般大于1000 kHz，这为磨削过程中噪声信号的分析提供了依据[11−13]。因此，首先对采集到的AE信号进行消噪处理。小波阈值降噪对非平稳信号的消噪有着无可比拟的优势[14]。本文即利用小波软阈值降噪对采集到的AE信号进行预处理。此外，磨削过程中的AE信号是复杂多变的，即使砂轮状态不变，瞬时弹性波也有很大的差别。分析特定时间点的AE 信号是没有意义的。所以，本文通过分帧处理将经过去噪的AE 信号划分为多个帧，以帧为单位去分析每帧信号与所对应的砂轮钝化状态之间的关系。需要注意的是，为了增加样本的数目，帧与帧之间允许有重叠。对已经划分好的每帧信号，要提取其AE信号特征，以表征该帧信号。本文中，提取振幅、持续时间、上升时间等典型的8 个AE 特征组成8 维样本向量。这些8 维样本向量将组成AE 数据集作为对原始AE信号的替代。另外，砂轮状态的变化是一个时间序列问题，隐半马尔可夫模型(HSMM)适用于这类问题[14]。HSMM 是隐马尔可夫模型(Hidden Markov models, HMM)的一个改进，避免了HMM状态驻留时间呈指数衰减的缺点，广泛应用于机械故障诊断、材料缺损等状态识别问题[15]。另外，磨削加工过程中的砂轮状态是持续变化的，如何将不间断变化的砂轮状态量化为几个确定的状态是磨削加工领域的一个难题。分层Dirichlet过程(HDP)有效地解决了这个问题。这种方法不需要给出砂轮状态的数目，而是通过AE 数据集自适应聚类获得状态划分，以得到整个磨削过程砂轮钝化程度的量化分级结果。以上所述磨削砂轮钝化状态检测方法如图1所示。小波阈值降噪、AE 信号特征以及HDP-HSMM的具体描述分别见第1.1 节、1.2 节、1.3节。

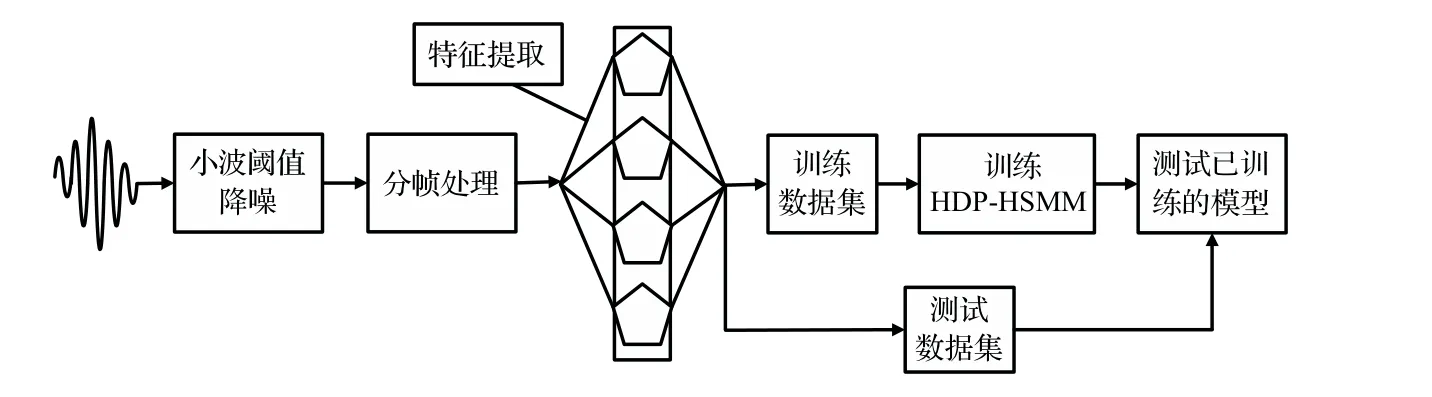
图1 磨削砂轮钝化状态检测方法流程图Fig.1 The flow diagram of monitoring method of the grinding wheel blunt state

1.1 小波阈值降噪

小波阈值降噪的具体方法如图2所示。首先，通过小波变换对含噪信号进行多尺度分解；然后，使用阈值函数对分解得到的多尺度小波系数进行阈值量化处理，即保留有用频带的小波分解系数，去除无用频带的噪声信号小波分解系数；最后，使用处理后的小波分解系数通过小波逆变换重构信号即得到了去噪之后的信号。

图2 小波阈值降噪原理图Fig.2 The schematic diagram of wavelet threshold de-noising

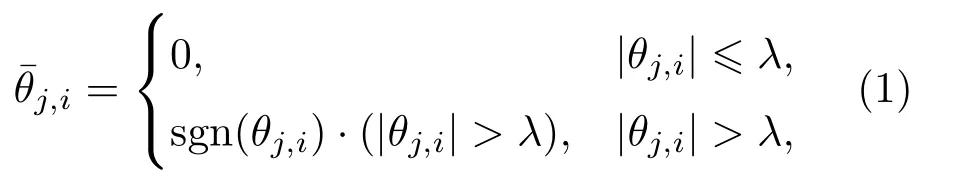
通过小波阈值去噪的方法对信号进行降噪的关键是阈值函数的选择和阈值门限的设置。常见的阈值函数有硬阈值、软阈值和半软阈值[16]。本文采用软阈值函数，其表达式如下：其中，θj,i为含噪信号的小波分解系数，λ为给定阈值。采用db5 小波软阈值降噪后的AE 信号对比如图3所示。可看出，去除其他噪声的AE 信号更清楚地显示了材料塑性变形所产生的声发射现象，图3(b)中的每个声脉冲均代表一次声发射过程，称作AE hit。

1.2 AE信号特征

对经过分帧得到的每帧AE 信号需要提取其AE 信号特征。对每帧AE 信号，通过一个门限电压(Threshold)截取到多个AE hit。图4即是由Threshold截取的一个AE hit。对每一个AE hit 都提取8 个特征，并求得该帧信号中所有AE hit 8 个特征的平均值作为对该帧AE 信号的替代。在AE检测技术中常用的AE 特征包括：撞击计数、振铃计数(Counts)、能量计数、幅度(Amplitude)、持续时间(Duration)、上升时间(Rise time, RT)、有效值(Root mean square, RMS)电压等。在本文中，使用幅度、持续时间、上升时间、能量计数、振铃计数、有效值电压、峰峰值(Peak-to-peak value, P2P)和偏度(Skewness, SK)共8个特征。幅度即AE hit信号波形的最大振幅值，通常要对其取对数，单位是dB。记作

持续时间即AE hit持续的时间间隔。上升时间就是一个AE hit 从发生到达到最高信号电平所持续的时间。能量计数即整个AE hit 波形包络的面积。振铃计数即AE hit越过门限信号的振荡次数。有效值电压就是AE hit信号电平的均方根值，表示为

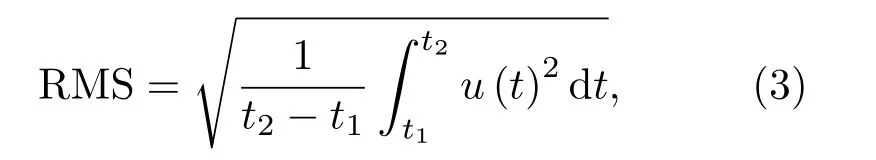
其中，u(t)就是AE hit的信号电平。峰峰值即是AE hit最高信号电平与最低信号电平差值的一半：

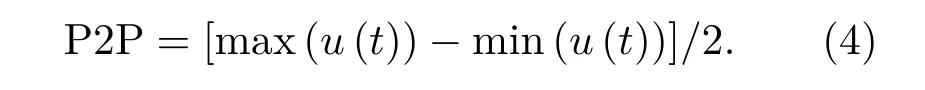
偏度表示AE hit 信号偏离中心的程度。当SK<0时，该AE hit 的波形左偏，反之右偏，SK = 0 是波形对称分布。其计算公式是用其三阶中心距除以标准差的三次方：

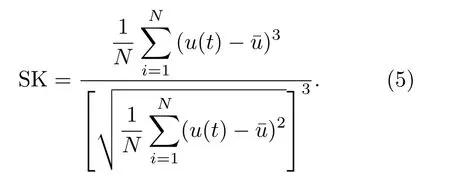
图4 AE hit 和典型的AE 特征Fig.4 AE hit and the typical AE features

1.3 HDP-HSMM

HMM是一种描述隐含未知参数马尔科夫过程的统计模型，可以有效地解决时间序列问题，但同时它也有两个明显的缺点[17]：(1) 状态驻留时间限制为不适用于真实数据的几何分布；(2) 必须指定一定数量的隐藏状态。

作为对HMM 的改进，HSMM 解决了真实数据不服从马尔科夫性的问题。图5即HSMM 的有向图[18]。zt之间的箭头表示隐藏状态转移，zt和yt之间的箭头代表观测和隐藏状态之间的对应关系。HSMM 由参数λ= (π,A,D,B)描述，其中π 代表初始状态概率，A代表隐状态转移概率矩阵，D代表状态驻留时间概率矩阵，B代表观测概率矩阵。对于D，需要指定一个非几何分布并通过训练数据集来学习分布参数[18]。

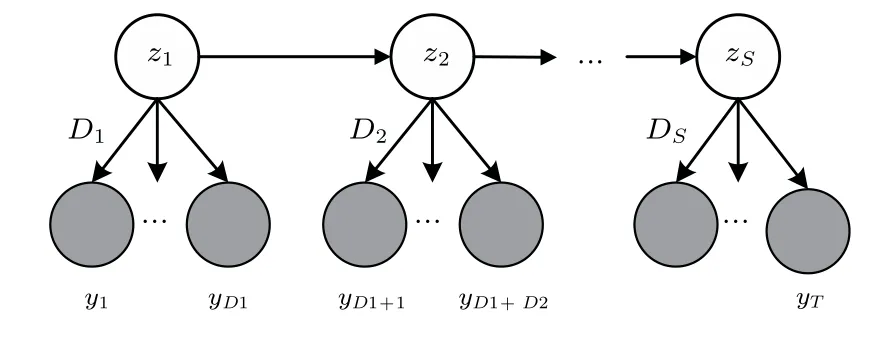
图5 隐半马尔科夫模型Fig.5 The HSMM

一个非参数贝叶斯模型HDP，解决了隐状态需要指定的问题。该模型使用HDP 作为在无限状态空间的先验，从而确保了复杂多变的隐状态推断和在多种不同模型下的贝叶斯混合[19]。结合HSMM能对实际数据进行时间序列标记和HDP 根据数据本身自适应聚类的特性，HDP-HSMM 被提出。其有向图模型如图6所示[17]。

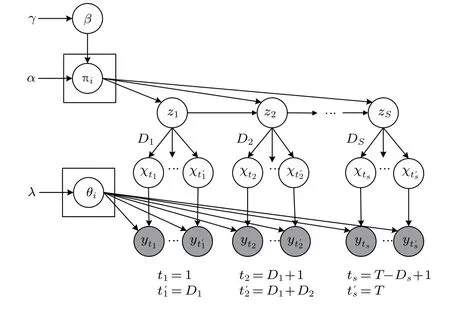
图6 分层Dirichlet 过程-隐半马尔科夫模型Fig.6 The HDP-HSMM

图6中的HDP-HSMM可记为[17]

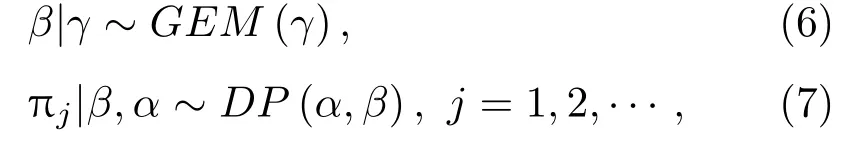
其中，GEM 指的是Stick-breaking 过程[19]；zt是隐状态序列；yt是服从分布f的观测序列；D表示状态驻留时间分布，H(λ)表示特定状态观测分布的参数，{j}来自于参数为λ的先验分布H。HDP 可视作一个无穷状态转移空间，每一个{j}都是一个Dirichlet 过程并且被解释为状态j的转移概率，即转移矩阵的第j行。状态j与一组参数为相同离散测度的Dirichlet 过程联系起来[17]。转移概率主要分布在几个典型的状态。

此外，条件随机场算法(Conditional random field algorithm, CRF)采样方法[17]提供了完整的无穷维HDP 的有效近似推断。但这种采样方法存在下列缺点[17,20]：(1)每个状态的转移必须独自重采样；(2)状态序列的强相关性显著降低了混合速度。因此，提出了一种可以避免混合速率降低的有限近似采样技术。本文采用的弱极限近似采样器[21]就是这样一种新的推断方法，它通过忽略无限转移概率矩阵的“小尾巴”来提高采样速率。

2 磨削砂轮钝化状态识别结果分析

本文搭建了AE 信号磨削砂轮钝化状态检测实验系统，如图7所示。响应范围为0 MHz∼3 MHz的全接触式AE 传感器由耦合剂固定在磨床机壳上。采用普通刚玉树脂砂轮的高精度轧辊磨床磨削加工高镍铸铁工件，所产生的AE信号被AE传感器接收并由安捷伦u2331 数据采集装置所采集，以二进制文件的形式存储在PC 机中。示波器实时显示采集的AE 信号。离线分析系统将对采集到的AE 信号进行处理，并由HDP-HSMM 学习整个加工过程的砂轮钝化状态序列，实现对整个磨削加工过程砂轮钝化状态的监控。

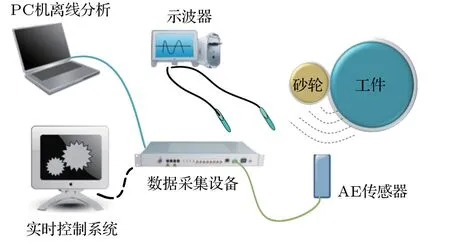
图7 磨削砂轮钝化状态检测装置Fig.7 The monitoring device of grinding wheel blunt state

2.1 AE信号特征提取

采集到的AE信号首先被db5软阈值小波降噪，其通带频率为100 kHz∼300 kHz。然后进行分帧处理，帧长设置为2 s，帧移设为1 s，故794 s的原始AE信号被划分为794帧。设置Threshold 为50 mV，提取每一帧中所有AE hit 的8 个特征并求其平均值，得到794个8维AE 数据集。这些AE数据集将作为训练数据集去学习HDP-HSMM。图8即是8 维AE特征数据集，隐含着砂轮钝化状态变化的信息。

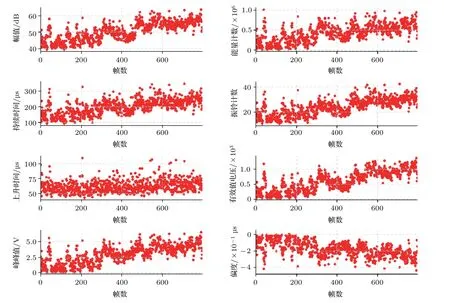
图8 8 维AE 特征数据集Fig.8 The 8 time-domain AE features data set

2.2 HDP-HSMM训练和砂轮钝化状态识别

使用2.1 节得到的AE 数据集， 通过HDPHSMM弱极限近似采样器去训练HDP-HSMM。同时设置如下的超参数：最大类别数目为10；观测概率分布函数为10组分高斯混合分布，即每一个隐状态的观测分布都是一个十组分混合高斯分布，其参数采样于一个Dirichlet 先验；状态驻留概率分布为泊松分布。基于以上设置，运行采样循环。对于每次循环，HDP-HSMM 所有的潜在变量将通过吉布斯采样算法[17]采样。这些变量包括状态转移概率矩阵、观测概率分布的均值和协方差、状态驻留概率分布的参数以及隐状态序列。对数似然随着采样循环的增加而增加，当采样循环达到70次时趋于收敛，如图9所示。这表明，HDP-HSMM 具有快速学习的能力，可用于实时在线数据处理。

进行200 次采样循环后得到的隐状态序列如图10 所示。图中横轴帧数代表磨削加工进行的时间，图10(a)中的不同颜色的竖条以及图10(b)中不同的数字表示砂轮的不同钝化状态，颜色越深，数字越大，砂轮钝化的程度就越严重。图10 中有4 种不同颜色和4 个不同的数字，这说明在整个加工过程中砂轮逐渐被磨钝，且划分4 个不同的钝化程度。尽管这些序列中有一些异常的状态变动，但整体上看状态划分依然很明确。另外，状态3 由于持续时间短，且状态变化较剧烈，可看作是状态2 和状态4的过渡期，不能视为一个砂轮钝化等级。故可认为在该磨削加工过程中，砂轮状态实际上只有3 个钝化等级，对应图10 中的状态1、状态2 和状态4，可分别称作1 级、2级和3 级钝化。通过以上分析可知，HDP-HSMM 通过训练AE 数据集较好地识别到了砂轮钝化状态随时间的变化过程，实现了对砂轮钝化程度的量化分级。

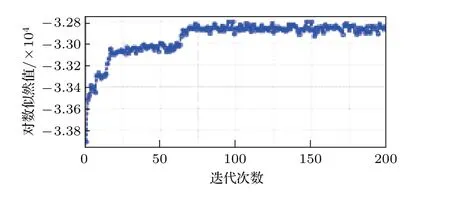
图9 HDP-HSMM 训练曲线Fig.9 The training curve of the HDP-HSMM

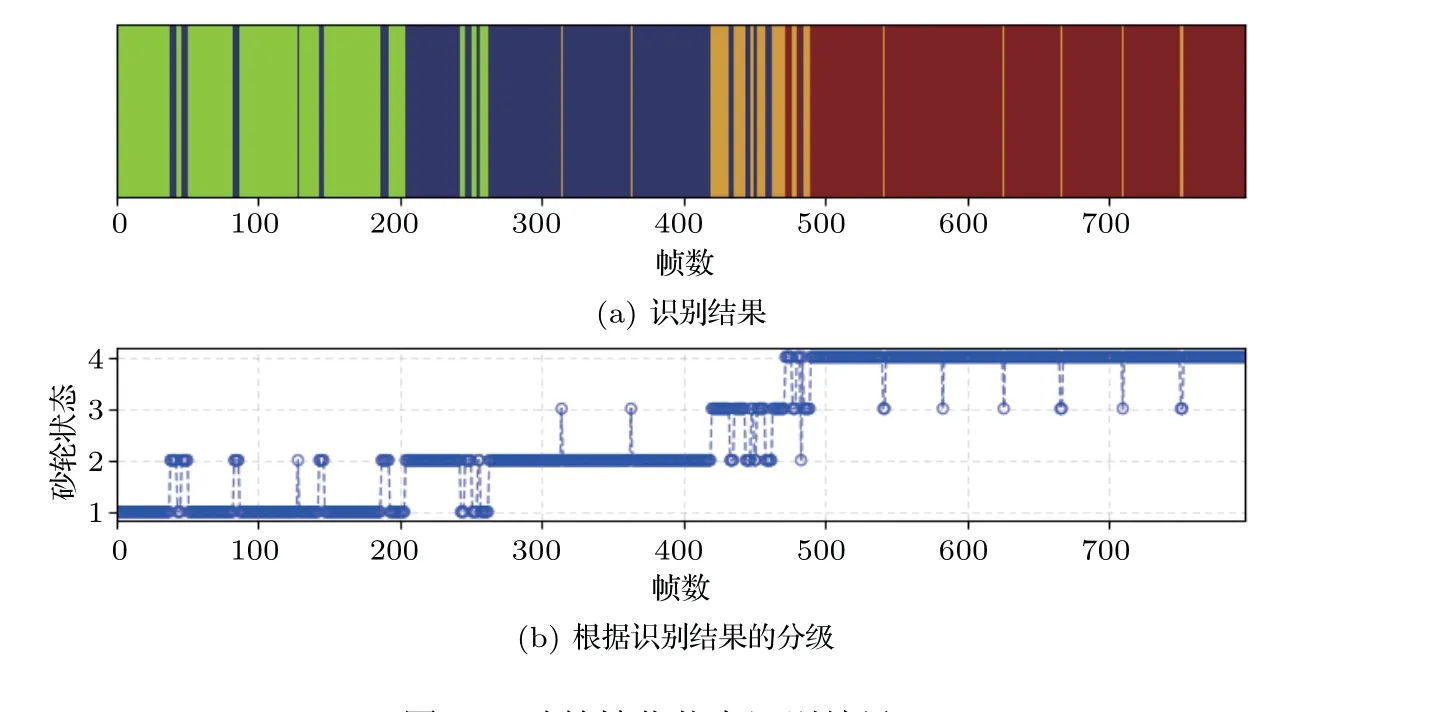
图10 砂轮钝化状态识别结果Fig.10 The identification result of the blunt state of the grinding wheel

2.3 模型验证

使用Viterbi 算法[17]测试已经训练好的模型，以验证HDP-HSMM 对训练数据集之外的数据的拟合效果，便于判断其在实际情况下的应用价值。Viterbi 算法是动态规划算法，基本原理是由当前时刻的最优状态序列推断下一时刻的状态，依次得到整个测试数据集的最优状态序列。取图10 中状态1、状态2 和状态4 即1 级、2 级和3 级钝化等级所对应的AE 信号段作为测试数据集去测试已训练好的HDP-HSMM。测试数据集的取法同训练数据集的取法稍有不同。对于同一段AE 信号，设置相同的帧移和帧长，由于分帧时起始点不同而得到不同的分帧结果，被认为是独立同分布的。因此，取同训练数据集不同的划分所得到的300个样本作为测试数据集，并将其钝化等级分别标记为1 级、2 级和3 级，去测试已训练好的HDP-HSMM。测试结果如表1所示，该测试结果显示由AE 数据集训练得到的HDP-HSMM 具有良好的泛化性能，其测试准确率达到93.7%。

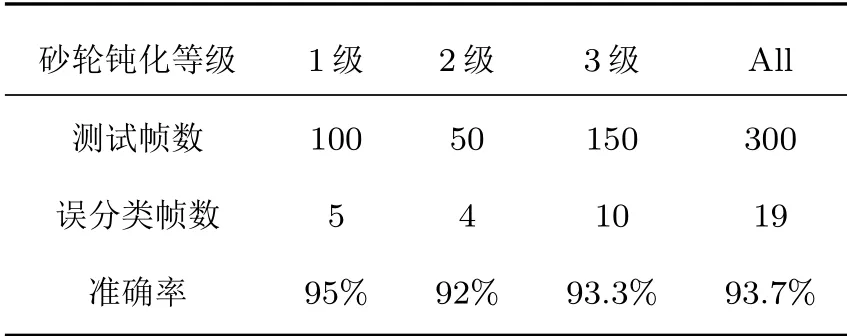
表1 已训练模型在测试数据集上的测试结果Table1 The test results of the trained model

3 结论和展望

本文提出了一种基于HDP-HSMM 的磨削AE信号砂轮钝化状态检测方法。首先，通过设计的磨削砂轮钝化状态检测实验采集到AE 信号。由磨削声发射机理，磨削AE 信号主要来源于材料塑性变形产生的弹性波，其频带为100 kHz∼300 kHz。因此，接下来对采集到的AE 信号进行db5 小波软阈值降噪。对于经过降噪的AE 信号进行分帧处理并提取每帧信号的8 个特征，组成8 维AE 数据集。最后使用AE 数据集作为训练数据集，并通过弱极限近似采样算法学习HDP-HSMM。其学习结果表明，该方法能够有效识别砂轮在加工过程中的状态变化并能对砂轮的钝化程度进行分级。其在测试数据集上具有93.7%的精度，具有很高的工业应用价值。

HDP-HSMM结合了显式时间分布的半马尔可夫模型和贝叶斯非参数技术，不仅可以对有监督和无监督的非马尔可夫时序数据学习，也可以对更大层次的模型进行推理。通过弱极限近似采样算法可以快速准确地对该模型进行训练。本文已经证明了该方法在磨削砂轮不同钝化状态识别中的有效性，这些方法也将可以为更多连续时间序列问题提供解决方案。