一种用于超声成像的零相位滤波后处理方法∗

韩晓丽 吴文焘 曹 政

(中国科学院声学研究所 北京 100190)

0 引言

超声相控阵系统中，声波信号在经过隔离、限幅、放大、滤波等模拟调理电路时必然会引入一定的噪声干扰[1]，因此，由A/D 采样后的数字信号在成像之前，必须要经过一定的滤波处理，以提高信噪比和成像质量[2−3]，也就是说，滤波是一个必备的处理过程。在对接收的回波信号进行分析的过程中，通常需要将信号不同成分进行分离，然后对不同成分做不同的处理或调整，从而最终提高对于缺陷或目标的检测能力[4]。大部分具有频率依赖性的检测识别算法的实现都需要辅以滤波处理的过程，包括超声检测系统广泛采用裂谱处理(Split spectrum processing, SSP)方法，从本质上讲，也是采用若干带通有限脉冲响应(Finite impulse response, FIR)滤波器进行滤波的过程[4−5]。

在超声无损检测领域，超声波遇到缺陷时会发生散射，在接收端会接收到经缺陷散射的回波信号，与缺陷有关的信号出现的时间即到达时间(Time of arrival, TOA)或传播时间(Time of flight, TOF)[4]恰恰能够反映缺陷在检测对象中所处的位置，以此来对缺陷进行定位。同时，为了保证系统检测的灵敏度和能够通过缺陷回波幅度在一定程度上估计缺陷的大小，要求缺陷回波波幅在滤波前后保持不变。基于上述两点，在对接收的回波信号进行滤波处理时，要保证滤波过程不影响主要频率成分的到达时间，这就需要滤波器具有零相位的相位响应特性。虽然FIR滤波器在单位脉冲响应序列h(n)满足一定的对称性时，具有线性相位特性[6−7]，但是滤波前后必然会出现一定的时延，难以满足零相位的要求。而无限脉冲响应(Infinite impulse response,IIR)滤波器不能实现严格意义上的线性相位特性。

除了直接设计具有零相位响应的数字滤波器以外，零相位滤波的过程还可以通过一种比较巧妙的方式实现，即采用前向-后向滤波-反向输出(Forward-reverse filtering, reverse output, FRR)[8]或反向滤波-反向输出(Reverse filtering,reverse filtering,RRF)的方法[9−10]。这种方法借助于两次滤波和信号翻转的组合，实现对输入信号的零相位滤波。鉴于FIR滤波器具有便于实现线性相位特性的优越性、系统稳定性好和使用上的灵活性[11]，通常大家习惯性地选用FIR 滤波器实现滤波过程，包括零相位滤波，也主要以FIR 的方式实现[10]。然而，由于FIR 滤波器传递函数的极点固定在原点，只能靠改变零点位置来改变它的性能。所以要达到高的选择性，必须用较高的阶数；对于同样的滤波器设计指标，FIR 滤波器所要求的阶数可能比IIR 滤波器高5∼10倍，信号延时也较大，处理效率低[11]。

近年来，在超声检测领域，实时缺陷检测的需求越来越高，要求系统能够尽快地实时采集、分析和处理超声波回波信号，这对于超声成像系统的实时性提出了更高的要求[5]。许多学者致力于探索如何高效地实现超声回波信号采集之后的滤波过程[12]，也包括开辟滤波器的高效硬件实现的新思路[5,10]。快速高效地实现零相位滤波，将有利于超声检测系统信号处理效率的提升，确保检测系统具有更高的实时性能。

本文针对在超声相控阵成像领域，在采用基于FIR滤波器的FRR零相位滤波时，由于FIR滤波器阶数高导致运算量大、处理效率低、难以满足实时性要求高的系统需求的问题，探讨在实际超声相控阵系统中使用IIR 滤波器实现FRR 零相位滤波的可行性，比较基于FIR和IIR 滤波器实现FRR零相位滤波的性能，探索IIR 滤波器实现FRR 零相位滤波时的效率提升程度，并且把IIR 零相位滤波应用于实时超声成像后处理系统中，通过实际的成像实验，验证使用IIR 滤波器实现FRR 零相位滤波的效果。

1 基于IIR的零相位滤波

根据线性系统理论，对信号进行经典线性滤波的过程对原始输入信号主要产生两大方面的影响[9]：一是对信号不同频率成分的幅值进行调整，通带内的频率成分一般不衰减甚至得到放大，而阻带内的成分通常被衰减，以减少这些成分在原始信号中所占的比重或影响，这是通过滤波器的幅频响应来实现的；二是对信号的不同频率成分产生相应的相移，这是通过滤波器的相频响应Arg[H(ejw)]来实现的。滤波器的线性相位指的是不同频率成分的时间延时是相同的，则总体上输出信号相对于输入信号不发生相位失真，仅发生一定的延迟。在超声相控阵成像系统中借助于零相位滤波正是巧妙地实现了对超声回波信号的滤波处理，同时保证群延时为零，即处理后的回波信号仍具有正确的到达时间。

借助于两次滤波和信号翻转的组合以实现零相位滤波的具体方法有两种：FRR 和RRF。FRR零相位滤波过程如图1所示。设滤波器单位脉冲响应序列h(n)，对应的Z变换(Ztransformation)为H(Z)。FRR先将输入序列x(n)按顺序输入到滤波器H(Z)中进行滤波，即前向滤波；然后将所得的结果序列y1(n)，翻转后得到序列y1(−n)，y1(−n)再次输入到滤波器H(Z)中，即反向滤波；再将所得结果y2(n)逆转后输出，即反向输出；最后得到精确的零相位失真的输出序列y(n)。RRF 先将输入信号序列反转后通过滤波器，然后将所得结果逆转后再次通过滤波器，这样所得结果即为精确零相位失真的输出序列[9]。不管是哪种具体方法都需要预先设计具有特定幅频特性的滤波器H(ejw)。

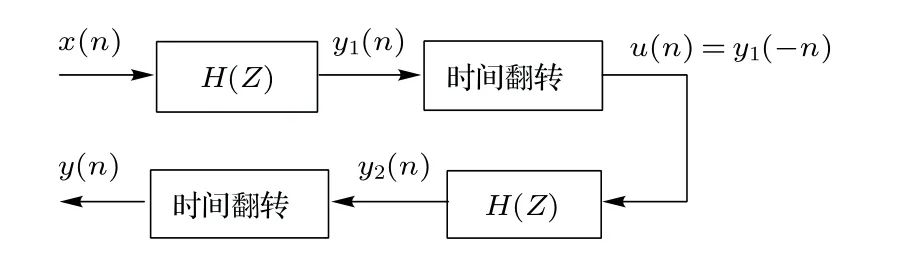
图1 FRR 零相位滤波过程Fig.1 Zero phase filtering based on FRR

FRR简单的推导过程[5]如下：

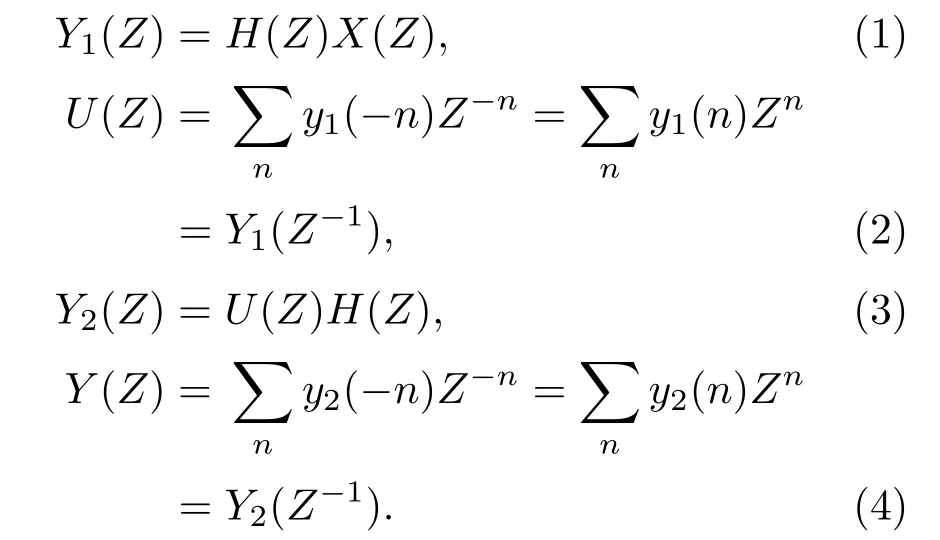
联立以上4 式，可以推得整个零相位过程的等效传输函数Heq(Z)：

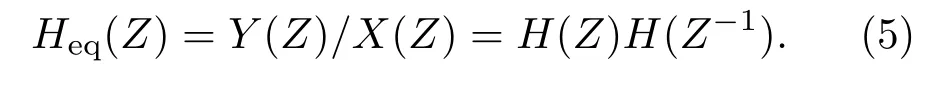
即等效系统频率响应为

也就是说，FRR 滤波过程真正实现了对输入信号x(n)的群延时为零的滤波处理，仅对其各频率成分进行了幅度调整。RRF 的推导过程与FRR 类似，这里不再赘述。因此，设计零相位滤波时，主要是设计满足特定需求的具有特定幅频响应特性的基础滤波器H(Z)。在上述推导过程中，并未指定滤波器H(Z)为有限脉冲响应滤波器(FIR)还是无限脉冲响应滤波器(IIR)。本文在后续章节中，将基于FIR 的FRR零相位滤波称为FIR FRR，将基于IIR的FRR零相位滤波称为IIR FRR。

2 IIR FRR零相位滤波的设计与分析

FRR 或RRF 的过程对输入信号的相位最终不产生影响，因此我们在设计基础滤波器H(Z)时主要关注其幅频特性，使其幅频特性满足我们的具体应用需求即可。下面以带通FRR 零相位滤波为例，设计IIR FRR和FIR FRR的基础滤波器H(Z)。FIR FRR主要用于与IIR FRR进行对比。

2.1 基础滤波器的设计

分别设计幅频特性参数如表1所示的FIR 和IIR 滤波器。前者采用等波纹(Equiripple)法，后者采用契比雪夫II (Chebyshev II)法。

设计的FIR 和IIR 滤波器的幅频响应曲线如图2所示。前者为57阶，即N=57，后者为12 阶，即N=12，其中Nb=12。在表1所示的幅频响应特性参数的约束下，两种情况设计的幅频响应曲线在通带内的形状差不多，主要差异在于低频范围内的通带到阻带的过渡带上，IIR 滤波器更窄。其中IIR 滤波器的零极点分布如图3所示。距离单位圆最近的极点是0.9484±0.2190 i。

表1 带通滤波器幅频特性描述参数Table1 Bandpass filter amplitude-frequency characteristic parameters

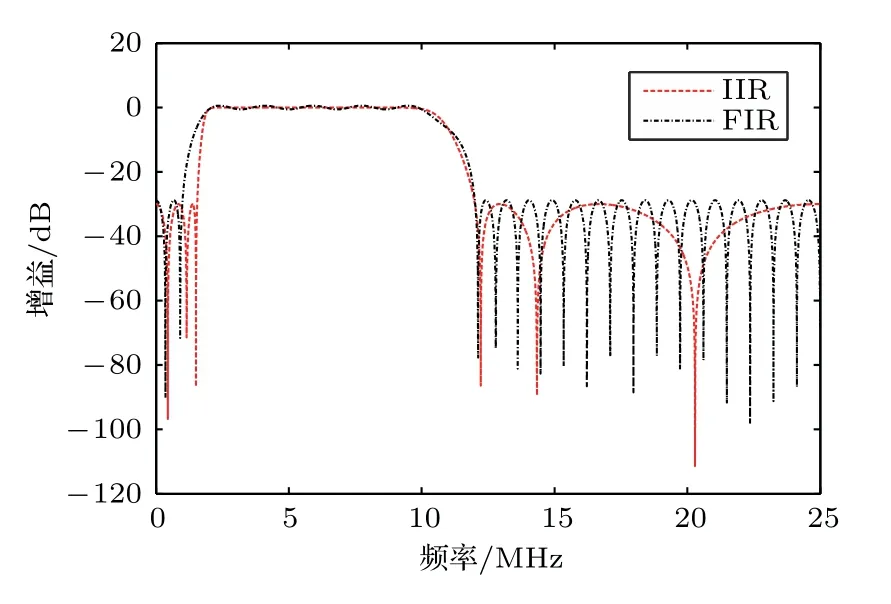
图2 IIR 和FIR 滤波器幅频特性曲线Fig.2 Amplitude-frequency curves of IIR and FIR filters

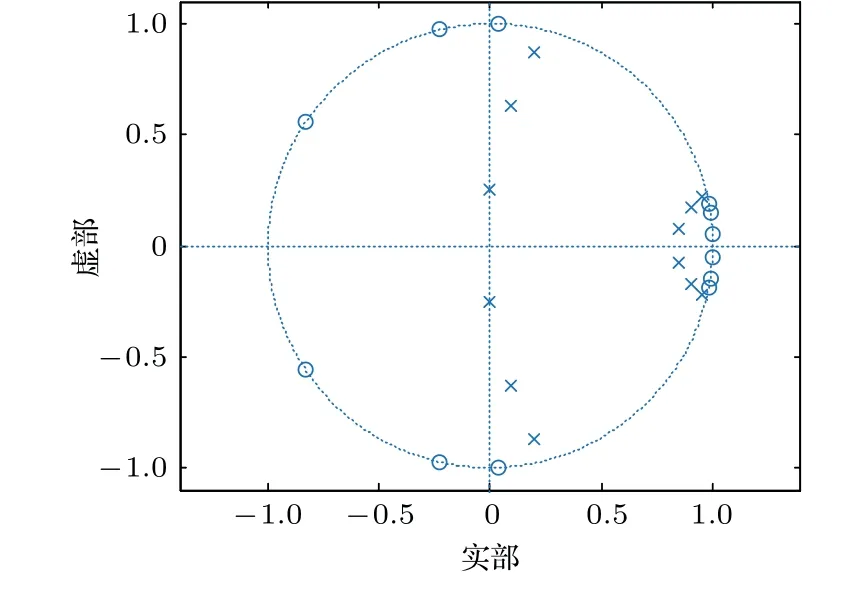
图3 IIR 滤波器零极点图Fig.3 Pole-zero diagram of IIR filter

2.2 FRR运算量分析

设x(n)为长度为Nx的因果序列， 即n ∈[0,Nx −1]。对于一个N阶的直接型FIR 滤波器，根据公式(7)可以推知，完成N阶的FIR 滤波需要的运算量为(N+ 1)(Nx −N+1)次乘法，N(Nx −N+1)次加法。

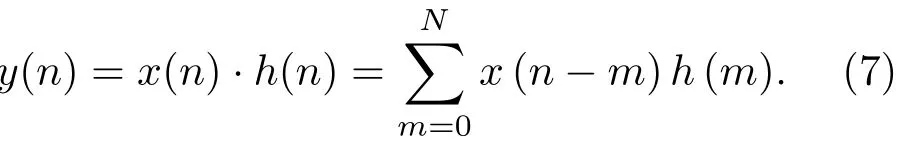
对于一个N阶的直接I 型IIR 滤波器，根据递推公式(8)可以推知，完成N阶的IIR 滤波需要的运算量[13]为(N+Nb+1)(Nx −N+1)次乘法，(N+Nb)(Nx −N+1)次加法。其中，Nb为IIR滤波器传输函数H(Z) 的分子多项式的阶数，需要注意的是，这里假定两种情况下输出序列的长度都仅取决于已知的输入序列x(n)和滤波器阶数，即输出序列y(n)的序列号范围均为n ∈[N,Nx]。

因此，上述的57阶FIR和12阶IIR滤波器直接I 型实现时的运算量如表2所示，其中，输出序列长度Ny=16384，输入序列长度Nx=16384+N −1。由此看出，理论上，前者的运算量约是后者的2倍多。

表2 FIR 和IIR 运算量理论值Table2 Amount of calculation comparison between FIR and IIR

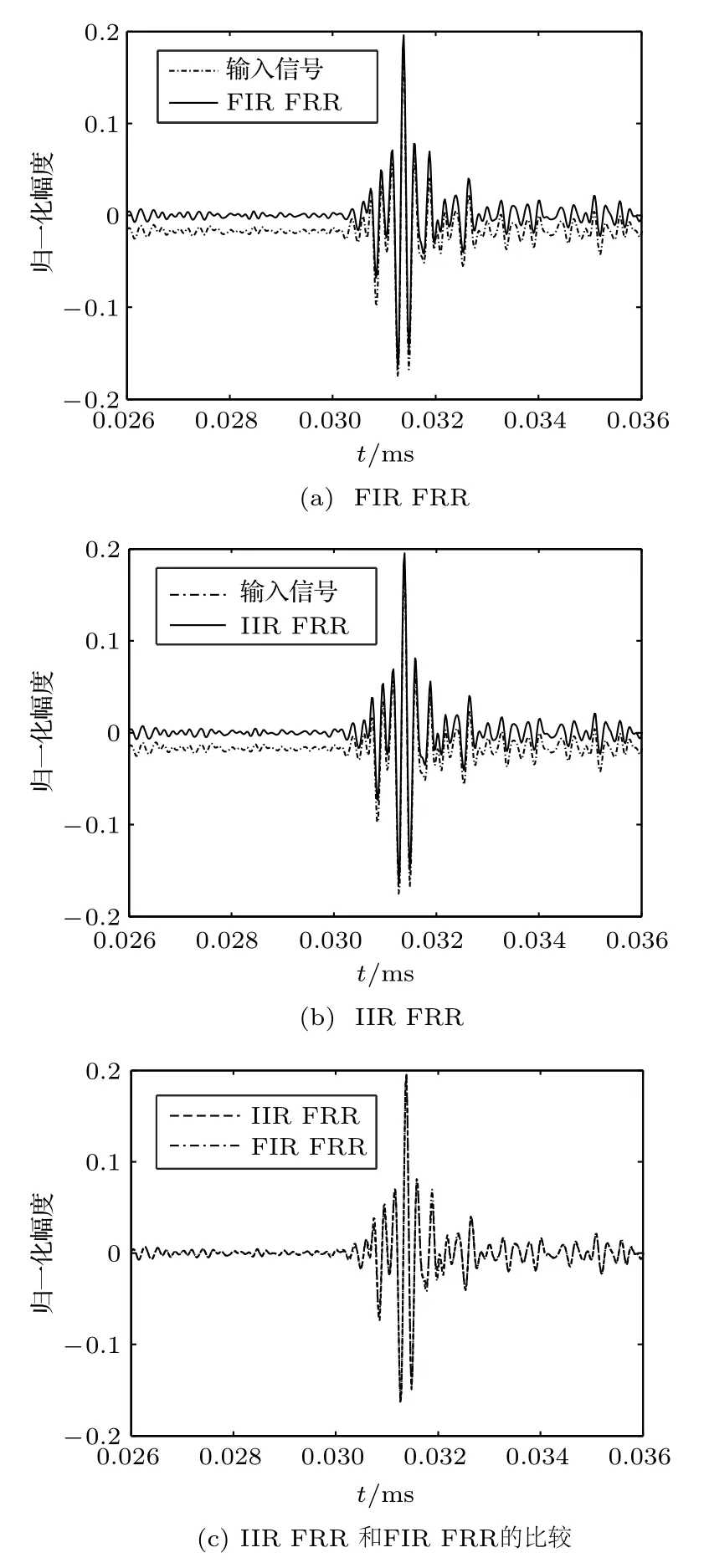
图4 FIR FRR 和IIR FRR 零相位滤波结果比较Fig.4 Comparison of zero-phase filtering results of FIR FRR and IIR FRR

在Matlab 中，利用设计的FIR 和IIR 滤波器对射频回波信号进行FRR 零相位滤波处理，对原始回波信号进行FIR FRR 和IIR FRR 的滤波结果如图4(a)和图4(b)所示。由图4可知，IIR FRR同FIR FRR 一样，也可以实现零相位滤波的功能。滤波前后，FIR FRR 和IIR FRR 的细节比较如图5所示，两种情况输出信号的时间位置相同，在幅度上只有较小的差异，造成差异的原因是两种滤波器的幅频特性曲线并不是完全相同的。因此，在几乎一致的幅频响应特性情况下，FIR 滤波器的阶数约为IIR滤波器阶数的5 倍，理论上的运算量约是IIR 滤波器的2倍多。

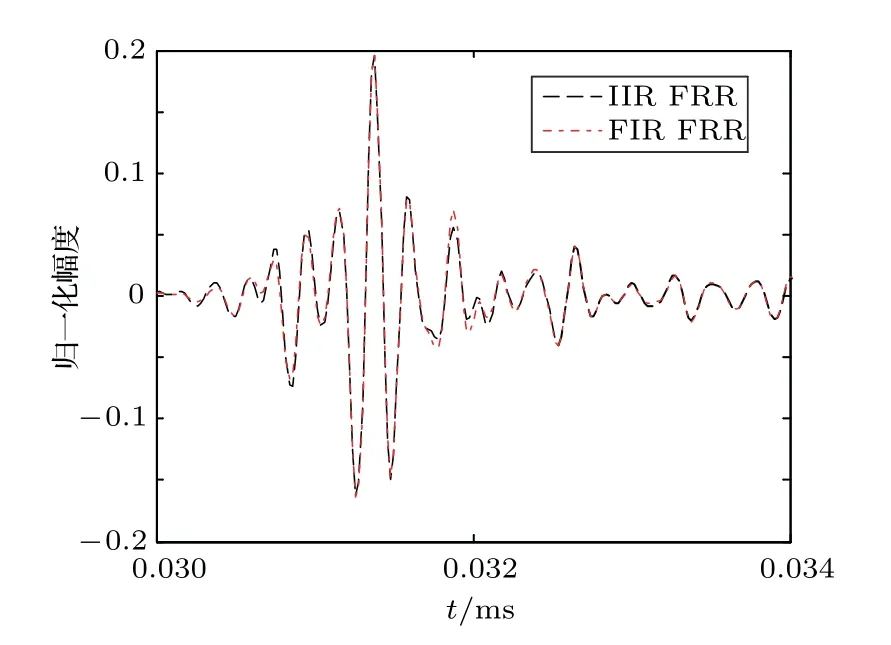
图5 FIR FRR 和IIR FRR 滤波结果的细节比较Fig.5 Detailed comparison of FIR FRR and IIR FRR results

3 IIR FRR用于超声成像后处理

为了比较IIR FRR 和FIR FRR 的超声成像效果，设计两组成像实验，分别利用FIR FRR 和IIR FRR对原始信号进行零相位滤波，然后经过相同的其他后处理后获得超声成像结果，并对结果进行比较。从原始数据到成像的整个后处理过程如图6所示。两组成像实验分别为：(1)单孔成像，(2)多孔成像。采用由课题组自主研发的UA special I 超声相控阵系统采集一帧原始回波数据，采集时使用的试块和换能器的放置形式如图7和图8所示。图7中，试块在深度25 mm 处有一个直径为1 mm 的通孔，相控阵换能器通过耦合剂与试块表面直接耦合，聚焦深度为25 mm。图8中的试块为标准的B 型便携式相控阵试块，由济宁模具厂生产，检测时换能器中心位于18−ϕ2 排孔最左侧两个孔的中间连线上，以18−ϕ2排孔为检测时的主要目标，聚焦深度设为50 mm。数据采样率为50 MSPS，超声相控阵换能器中心频率为5 MHz。

图6 超声成像后处理过程Fig.6 Post-processing of ultrasonic imaging involving zero-phase filtering

图7 数据采集时试块和换能器位置示意图——单孔Fig.7 Test block and transducer position during data acquisition (single hole)

图8 数据采集时试块和换能器位置示意图——多孔Fig.8 Test block and transducer position during data acquisition (a row of holes)

3.1 基于IIR FRR 的超声成像

利用图7情况下采集的回波数据集，经过图6所示的处理过程，其中的零相位滤波的过程分别利用FIR FRR 和IIR FRR 完成，最终形成如图9所示的单孔成像结果。由图9可知，经FIR FRR 和IIR FRR 处理后的数据的成像效果几乎完全相同，视觉上难以分辨差异。

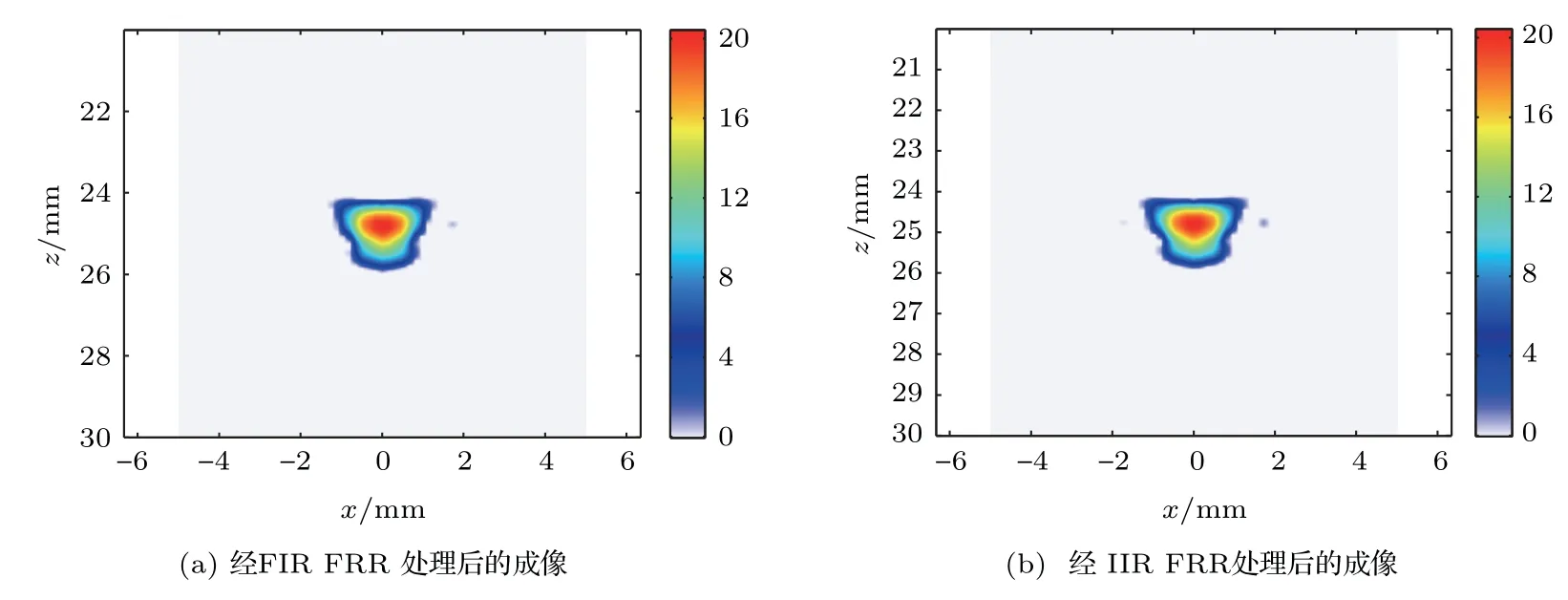
图9 FIR FRR 和IIR FRR 成像结果——单孔Fig.9 Imaging based on FIR FRR and IIR FRR (single hole)

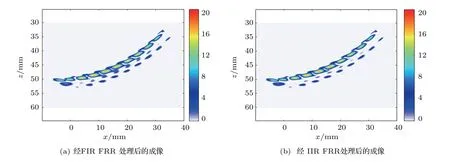
图10 FIR FRR 和IIR FRR 成像结果——多孔Fig.10 Imaging based on FIR FRR and IIR FRR (a row of holes)

另外，利用图8情况下采集的回波数据集，经过图6所示的处理过程，其中的零相位滤波分别利用FIR FRR 和IIR FRR 完成，最终对18−ϕ2 排孔形成如图10所示的成像结果。由图10可知，在复杂的多孔成像情况下，经FIR FRR 和IIR FRR 处理后的数据的成像效果也几乎完全相同，仅在18−ϕ2后方的伪影处存在极其细微的差别，这是由于两种滤波器的幅频特性曲线并不是完全相同导致的。

由成像结果可以看出，IIR FRR 可以实现与FIR FRR几乎相同的零相位滤波性能，得到几乎一致的超声成像效果。

3.2 算法实时性的验证

系统后端采用8 核处理器TMS320C6678 进行处理，利用定时器统计连续执行1000 次FIR FRR和IIR FRR 零相位滤波的时间，然后计算平均一次FRR 零相位滤波的时间。57 阶FIR 和12 阶IIR 采用直接I 型网络结构实现，数据格式采用浮点格式，其中，输出序列y(n)的长度Ny= 16384，输入序列x(n)长度Nx=16384+N −1。统计结果如表3所示。需要注意的是，在统计时间时，保持两种滤波过程采用相同的程序结构来实现，保证调用相同的函数，以及在调用函数时保证采用相同的调用格式，以保证在两种情况下，滤波算法的结构、实现的具体方式是相同的，从而尽可能减少其他因素对处理时间的影响。

从表3中可以看出：基于12 阶IIR 的FRR (直接I) 比FIR FRR (直接I) 耗时少，后者是前者的1.71 倍。

表3 FIR FRR 和IIR FRR 耗费的时间对比Table3 Time consumed during FIR FRR and IIR FRR

4 讨论

(1)处理时间

从理论角度分析，实现幅频响应类似的滤波，IIR 确实相比FIR运算量低很多，如表2所示。保守来讲，IIR甚至仅为FIR的1/2。

由表3可知，采用直接型I 结构实现高阶IIR 滤波器时，相对于采用直接型结构的FIR，IIR FRR的处理效率优于FIR FRR。对比表2和表3，相比基于57 阶FIR 的FRR，基于12 阶的IIR(直接I 型)的FRR 处理时间确实更短，但并没有达到约2 倍多的处理效率的提升。这是因为FRR 的过程包括两次滤波和两次序列的翻转，滤波耗时只是FRR处理总时间的一部分，在硬件处理器上执行FRR算法的时间，不仅包括完成两次FIR 或IIR滤波的时间，还包括序列翻转的时间。这些时间导致最终统计的时间效率比值不可能达到实现IIR 和FIR滤波器本身的时间效率比。

(2)稳定性

由于IIR 滤波器存在极点，如图3所示。当极点取值在单位圆内时，理论上IIR 滤波器是稳定的。但是在硬件处理器上实现时，滤波参数的量化或截断效应可能会引起实际滤波器极点位置的偏移，从而会引起滤波器出现不稳定的情况。在定点处理器中，这种问题尤为突出。但是FIR 滤波器由于只存在零点，不会出现不稳定的问题。从这个角度上说，FIR 滤波器实现起来更容易，更稳定，对参数数据占位宽度或精度的要求更低。因此基于IIR 的FRR更适用于浮点处理器。

5 结论

基于IIR FRR 零相位滤波可以实现与FIR FRR 相当的处理效果。当IIR 滤波器采用直接I型结构直接实现时，相对于FIR FRR，IIR FRR 可以在保证成像效果的前提下，将处理效率提升近1倍。在实际实时超声成像系统中，为了获得更高的处理效率，实现更高的帧率，可以选择采用IIR FRR零相位滤波取代FIR FRR。尤其在浮点型硬件处理器中，采用直接型IIR 实现FRR 零相位滤波，可以一定程度上提高处理效率。在实际应用中，需要仔细权衡FIR FRR 和IIR FRR 零相位滤波器在性能、时效、精度、稳定性、可控性、占用内存等多方面的要求，合理选择采用何种方式实现零相位滤波处理。