分数阶Langford系统的稳定性分析

朱香梗，李玉霞2，武 波

(1.山东科技大学 数学与系统科学学院，山东 青岛 266590;2.山东科技大学 电气与自动化工程学院，山东 青岛 266590)

分数阶微积分是对整数阶微积分的推广，整数阶微积分可以看成是分数阶微积分的特例，因此研究分数阶微积分更具有普遍意义[1]。在描述复杂物理学问题时，与非线性模型相比较，分数阶模型的物理意义更清晰，表述更简洁[2]。分数阶控制随着分数阶导数的不同可以增大控制的自由度，从而可获得更优良的控制性能；另一方面，分数阶微积分具有记忆功能，这种记忆功能确保历史信息对现在和未来的影响，有利于改善控制的品质[3-4]。

三维动力系统在非线性电路、生物网络以及信息安全等领域有着巨大的应用潜力，现已成为非线性科学理论与应用研究的热点[5-7]。随着现代数学研究的不断发展，分数阶系统动力学的研究引起了广泛关注，产生了一系列重要的研究成果，包括稳定性分析、分岔与混沌等[8-10]。近年来，分数阶系统在系统控制、粘弹性阻尼、电解质极化、分形与混沌和机器人等领域得到了广泛推广和应用，这一推广在跨学科领域的应用中表现尤为普遍[11-12]。

Langford系统是Langford W.F.根据Hopf建立的湍流模型演变而来的，研究表明，该系统具有丰富的非线性动力学行为。文献[13]对Langford系统中的规则运动进行定性分析，研究了Langford系统的混沌特性、Hopf分岔以及极限环的稳定性，并给出了全局分岔图。Nikolov等[14]给出了Langford系统的第一个Lyapunov值的具体表达式，并首次得到一个混沌解[14]。目前，对于Langford系统的研究结果仅限于整数阶，对分数阶Langford系统的研究较少。本研究基于Lyapunov稳定性定理，着重分析分数阶Langford系统的稳定性，给出系统保持稳定的条件。研究结果将有助于丰富Langford系统的稳定性理论，为进一步讨论分数阶Langford系统的控制问题提供参考意义。

1 分数阶Langford系统的数学模型

分数阶微积分有多种定义， 常用的定义有三种，即：Caputo定义、 Grunwald-Letnikov 定义和Riemann-Liouville定义。由于Caputo导数只需根据整数阶导数给出的初始条件即可表示实际情况中良好的特性，更适用于工程问题，因此本研究基于Caputo导数定义。

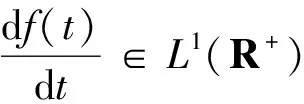
(1)

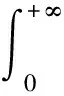
首先引入分数阶线性系统的稳定性定理。

引理1[16]对于下面的分数阶自治系统：

(2)

其中0<α<1，x∈Rn且A∈Rn×n，如果矩阵A的所有特征值λ满足|arg(λ)|>απ/2，则系统 (2) 的零解是渐近稳定的。

文献[17]考虑了如下Langford系统：

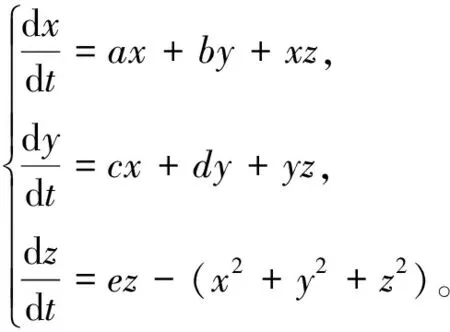
(3)

其中a,b,c,d,e表示系统参数。易见，系统 (3) 具有两个平衡点O(0,0,0)和E(0,0,e)。

利用分数阶Caputo微分定义将上述系统转化为分数阶，得到分数阶Langford系统数学模型如下：

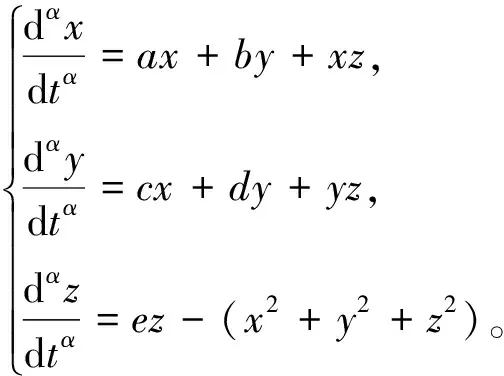
(4)

其中α∈(0,1]。

2 Langford系统在平衡点处的稳定性

2.1 系统在平衡点O(0,0,0)处的稳定性

易见系统 (4) 对应的雅可比矩阵为：

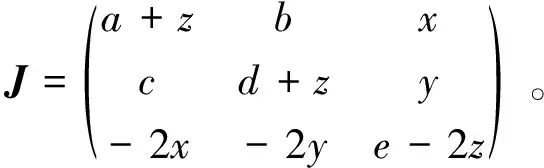
将平衡点O代入，可得此时雅可比矩阵为：

J1对应的特征方程为：

p1(λ)=(λ-e)[λ2-(a+d)λ+(ad-bc)]。

(5)

记

Δ1=(a+d)2-4(ad-bc)。

则特征方程(5)的特征根分别为：

下面，通过讨论参数a,b,c,d,e的取值范围来分析特征方程(5)根的正负性。

引理2对于特征方程(5)，可知：

1) 当Δ1>0且ad-bc≠0时，特征方程(5)的所有根都为实数：

① 如果e>0，ad-bc>0且a+d>0，则特征方程(5)有三个正实根；

② 如果e>0，ad-bc>0且a+d<0，则特征方程(5)有一个正实根，两个负实根；

③ 如果e>0且ad-bc<0，则特征方程(5)有两个正实根，一个负实根；

④ 如果e<0，ad-bc>0且a+d>0，则特征方程(5)有两个正实根，一个负实根；

⑤ 如果e<0，ad-bc>0且a+d<0，则特征方程(5)有三个负实根；

表1 特征方程(5)的根在空间(a,b,c,d,e)中的分布Tab.1 Distribution of roots of Eq.(5) in (a,b,c,d,e)-space

⑥ 如果e<0且ad-bc<0，则特征方程(5)有两个负实根，一个正实根。

2)当Δ1<0且ad-bc≠0时，特征方程(5)有一个实数根和一对复共轭根：① 如果e>0且a+d>0，则特征方程(5)有一个正实根和一对复共轭根，其中复根的实部均为正数；② 如果e>0且a+d<0，则特征方程(5)有一个正实根和一对复共轭根，其中复根的实部均为负数；③ 如果e<0且a+d>0，则特征方程(5)有一个负实根和一对复共轭根，其中复根的实部均为正数；④ 如果e<0且a+d<0，则特征方程(5)有一个负实根和一对复共轭根，其中复根的实部均为负数。

由引理2可以看出曲线Δ1=0,e=0,ad-bc=0,a+d=0将空间(a,b,c,d,e)分成了如表1中的10个区域。易得：

定理1分数阶Langford系统在平衡点O(0,0,0)处的稳定性结论如下：

1) 如果(a,b,c,d,e)∈Ω5∪Ω10，则系统(4)在平衡点O(0,0,0)处对任意的α∈(0,1]都是局部渐近稳定的；

2) 如果(a,b,c,d,e)∈Ω1∪Ω2∪Ω3∪Ω4∪Ω6∪Ω7∪Ω8，则系统(4)在平衡点O(0,0,0)处对任意的α∈(0,1]都是不稳定的；

3) 如果(a,b,c,d,e)∈Ω9且α满足下面的不等式

(6)

则系统 (4) 在平衡点O(0,0,0)处是局部渐近稳定的；

4) 如果(a,b,c,d,e)∈Ω9且α满足下面的不等式

(7)

则系统 (4) 在平衡点O(0,0,0)处是不稳定的。

证明：由引理1，易得如下结论

1) 如果(a,b,c,d,e)∈Ω5∪Ω10，则式(5)的所有实特征根和共轭特征根的实部都为负数。这意味着方程 (5) 的所有特征根都在稳定域内。因此，系统(4)在平衡点O(0,0,0)处是局部渐近稳定的。

2) 如果(a,b,c,d,e)∈Ω1∪Ω2∪Ω3∪Ω4∪Ω6∪Ω7∪Ω8，则方程 (5) 至少有一个正实根。因此系统 (4) 在平衡点O(0,0,0)处是不稳定的。

3) 如果(a,b,c,d,e)∈Ω9, 则特征方程(5)有一对具有正实部的复共轭特征根λ2,3以及一个负实根λ1，分别为：

进而有

因此，若满足式(6)，则系统 (4) 在平衡点O(0,0,0)处是局部渐近稳定的。

4) 由3)中的推论可知，若 满足式(7)，则系统(4)在平衡点O(0,0,0)处是不稳定的。

2.2 系统在平衡点E(0,0,e)处的稳定性

系统在平衡点E(0,0,e)处的雅可比矩阵为：

J2对应的特征方程为：

p2(λ)=(λ+e)[λ2-(a+d+2e)λ+(a+e)(d+e)-bc]。

(8)

记

Δ2=(a+d+2e)2-4[(a+e)(d+e)-bc],μ0=(a+e)(d+e)-bc。

特征方程 (8) 的特征根分别记为：

下面通过讨论参数a,b,c,d,e的取值范围来分析特征方程(8)的根的特性。

引理3对于特征方程 (8)，有如下结果：

1) 当Δ2>0且μ0≠0时，特征方程(8)的所有特征根都为实数：

① 如果e>0，μ0>0且a+d+2e>0，则特征方程(8)有两个正实根，一个负实根；

② 如果e>0，μ0>0且a+d+2e<0，则特征方程(8)有三个负实根；

③ 如果e>0，μ0<0，则特征方程(8)有两个负实根，一个正实根；

④ 如果e<0，μ0>0且a+d+2e>0，则特征方程(8)有三个正实根；

⑤ 如果e<0，μ0>0且a+d+2e<0，则特征方程(8)有两个负实根，一个正实根；

⑥ 如果e<0，μ0<0，则特征方程(8)有两个正实根，一个负实根；

2) 当Δ2<0且μ0≠0时，特征方程(8)有一个实数根和一对复共轭根：

① 如果e>0且a+d+2e>0，则特征方程(8)有一个负实根和一对实部为正的复共轭特征根；

② 如果e>0且a+d+2e<0，则特征方程(8)有一个负实根和一对实部为负的复共轭特征根；

表2 特征方程(8)的根在空间(a,b,c,d,e)中的分布Tab. 2 Distribution of roots of Eq.(8) in (a,b,c,d,e)-space

③ 如果e<0且a+d+2e>0，则特征方程(8)有一个正实根和一对实部为正的复共轭特征根；

④ 如果e<0且a+d+2e<0，则特征方程(8)有一个正实根和一对实部为负的复共轭特征根。

由引理3可以看出曲线Δ2=0,e=0,μ0=0,a+d+2e=0将空间(a,b,c,d,e)分成了如表2所示的10个区域。

由引理3，可得系统(4)在平衡点E(0,0,e)处的稳定性结果。

定理2

1) 如果(a,b,c,d,e)∈S2∪S8，则系统(4)在平衡点E(0,0,e)处对所有的α∈(0,1]都是局部渐近稳定的。

2) 如果(a,b,c,d,e)∈S1∪S3∪S4∪S5∪S6∪S9∪S10，则系统(4)在平衡点E(0,0,e)处对所有的α∈(0,1]都是不稳定的。

3) 如果(a,b,c,d,e)∈S7且α满足下列不等式

则系统 (4) 在平衡点E(0,0,e)处是局部渐近稳定的。

4) 如果(a,b,c,d,e)∈S7且α满足下列不等式

则系统 (4) 在平衡点E(0,0,e)处是不稳定的。

证明：同定理1的证明，此处不再赘述。

3 数值仿真

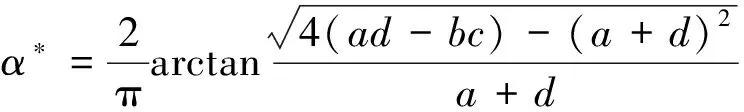
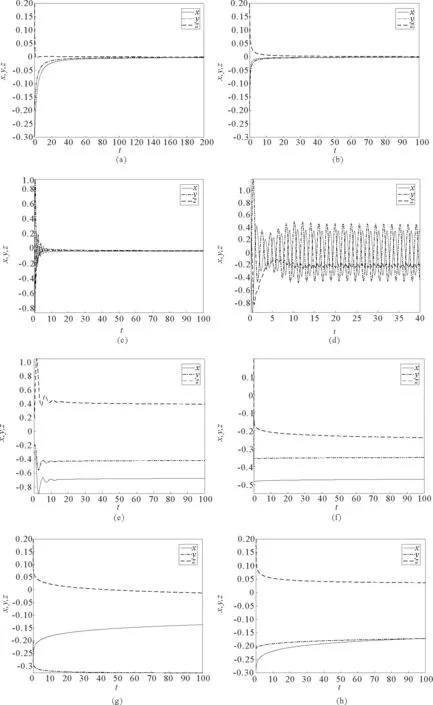
图1 Langford系统在平衡点处的稳定性Fig.1 Stability of Langford system at equilibrium point

图1(d)～1(h)表明系统(4)在平衡点O(0,0,0)处是不稳定的，其中图1(d)与1(c)的系统参数值相同，只改变阶数α，图(d)的阶数取值为α=0.8>α*；图1(e)的系统参数取值为(a,b,c,d,e)=(-1,1,1,-2,2)∈Ω2，阶数取值为α=0.6；图1(f)的系统参数取值为(a,b,c,d,e)=(0.4,0.2,0.3,0.2,-0.1)∈Ω4，阶数取值为α=0.03；图1(g)的系统参数取值为(a,b,c,d,e)=(0.01,-0.3,0.1,0.2,0.1)∈Ω7，阶数取值为α=0.1；图1(h)的系统参数取值为(a,b,c,d,e)=(-0.01,-0.3,0.1,-0.2,0.1)∈Ω8，阶数取值为α=0.2。

4 结论

分数阶非线性系统的稳定性对实际应用问题有着十分重要的作用，本研究利用Caputo分数阶微分定义将三维整数阶Langford系统推广到分数阶上，并通过对系统参数的讨论判断了系统的稳定性，最后用Matlab进行数值仿真验证所得定理的正确性。