海洋平台大直径钢管桩溜桩区间计算方法

2

(1.山东科技大学 土木工程与建筑学院, 山东 青岛 266590；2.山东科技大学 山东省土木工程防灾减灾重点实验室, 山东 青岛 266590)

海洋平台作为提供生产与生活设施于一体的构筑物，集钻井、运输、施工、观测、导航于一身。其桩基施工一般使用大直径超长钢管桩，通过液压打桩锤将管桩沿导管打入海底土层。打桩过程中，当钢管桩遇到海洋土层中的软弱土层时，由于桩端阻力与桩侧摩阻力减小，经常会发生溜桩现象。溜桩不仅影响成桩质量与桩基承载力，而且还会使桩的实际贯入度与桩基的设计高程产生较大误差。

近年来，国内外学者对溜桩问题开展了一系列研究。郭生昌等[1]结合工程实际分析了溜桩原因，并提出了相应的预防措施；孙立强等[2]考虑桩周土体的强度折减和超孔压等因素，提出了溜桩长度的计算方法；尹汉军等[3]采用静力平衡法对溜桩区间进行了估算；Dover等[4]提出了一种溜桩预测方法，并对26根管桩的溜桩可能性进行了预测；闫澍旺等[5]分析了大直径钢管桩的溜桩机理，并提出了溜桩长度的计算方法。以上研究大多是针对钢管桩溜桩过程中桩侧摩阻力的折减和溜桩长度的计算开展的，很少考虑溜桩过程中不同深度桩侧摩阻力的变化，且没有针对实际工程情况采用不同的溜桩计算方法。

针对以上问题，首先对海洋平台大直径钢管桩的溜桩原因进行了分析，然后考虑溜桩对不同深度桩侧摩阻力的影响，计算得到地基极限承载力与桩端阻力的关系，进而采用静力平衡与功能原理建立了大直径钢管桩溜桩区间的新计算方法，并通过工程实例进行了对比分析，验证了计算方法的合理性和可靠性。

1 溜桩原因分析

工程实践[6]表明，溜桩通常会在以下两种情况下发生：一是当海洋土体表层为承载力较弱的软土层；二是桩从承载力较高的土层打入承载力较小的土层时。由于海洋土体的性质，每根钢管桩在打桩过程中溜桩发生的次数会在0到3次之间。

当钢管桩刚进入海洋表面土层时，由于土层承载力较弱，在桩锤未锤击的情况下，桩自由贯入土层一定深度。当桩进入硬质土层时，桩端阻力与侧摩阻力变大，钢管桩在锤击作用下逐渐贯入土中。当桩进入软黏土层中，桩端阻力减小，桩侧摩阻力不足以承受桩与桩锤的质量，此时桩会在未锤击的情况下贯入土层，即桩体发生溜桩。当桩进入硬质土层或桩侧摩阻力增加到一定值时，溜桩停止。当桩继续贯入时，虽然侧摩阻面积增加，但由于土体的重塑，桩侧摩阻力实际上是不断减小的。所以当再次进入软土层中，会发生二次溜桩现象。图1为溜桩现象示意图。

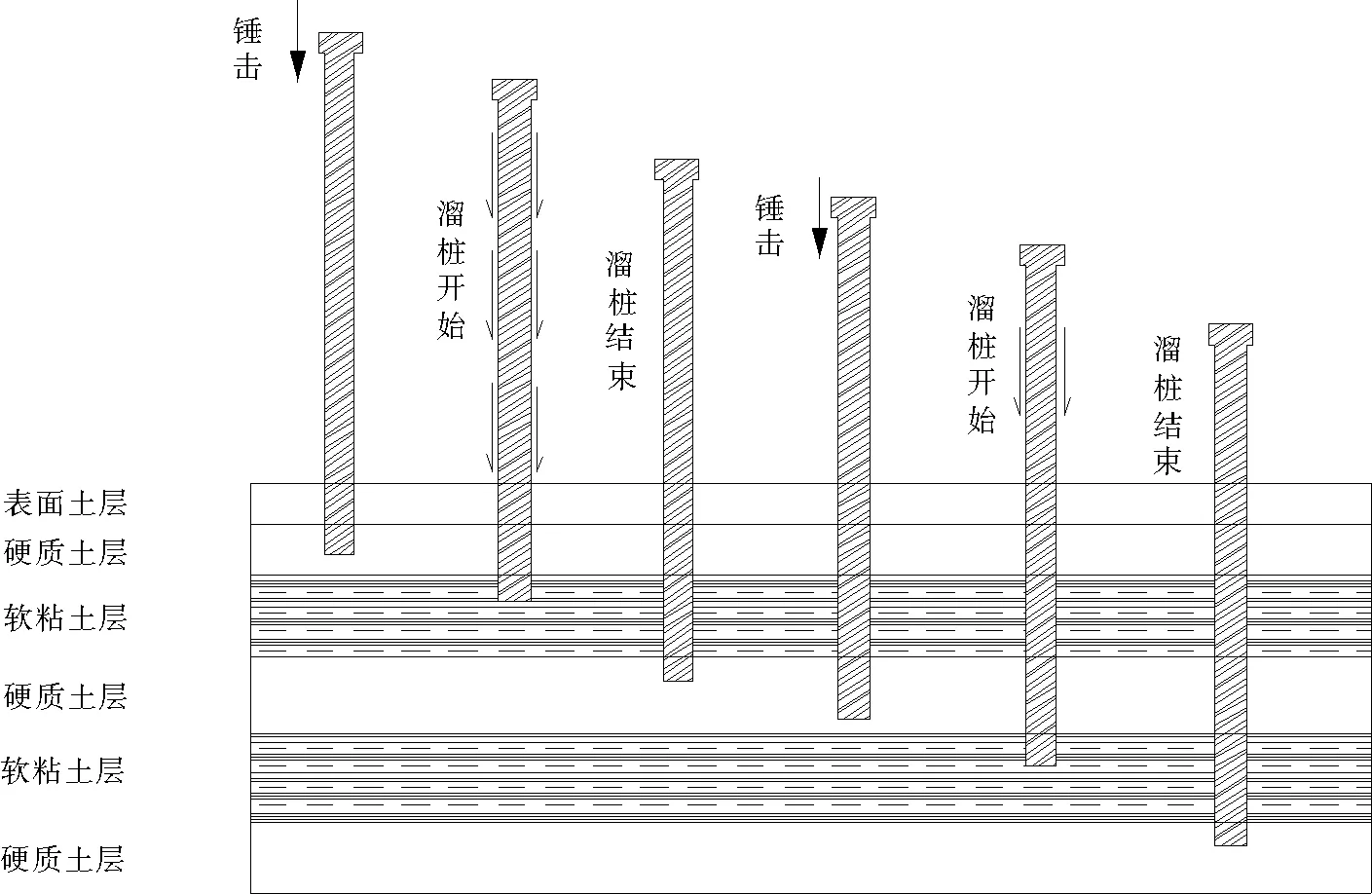
图1 溜桩现象示意图

当桩体受到的总土阻力满足以下条件之一时便有可能发生溜桩：①总土阻力小于桩身自重；②总土阻力小于桩与桩锤的重力；③总土阻力小于桩与桩锤的惯性力。

2 沉桩阻力计算

2.1 桩端阻力的计算

对于溜桩过程中大直径钢管桩受到的桩端阻力，可以通过求环状桩端受到的土阻力得到。砂土层中的环状桩端阻力采用别列柴策夫公式[7]计算，将计算得到的桩的环形端部截面的极限承载力视为桩端阻力。

根据别列柴策夫计算公式，砂土层中桩端阻力

qu=qDNq+γBNr。

(1)

式中：qu为桩端阻力，kPa；Nq，Nr为地基极限承载力系数，通过土体的内摩擦角φ确定；qD为地基处的超载，kPa；B为钢管桩的直径，m；γ为土层浮容重，kN/m3。地基极限承载力系数见表1。

表1 地基极限承载力系数表

对于钢管桩在黏性土中受到的环状桩端阻力，可通过qu=Nrcu进行计算，cu为黏土的不排水抗剪强度，kN/m2。Som等[8]通过实验和分析提出在黏性土中Nr取9比较合适，因此黏性土中桩端阻力为：

qu=9cu。

(2)

2.2 桩侧摩阻力的计算

通过对溜桩现象的分析[9]可以得到，在桩贯入土体的过程中，桩底部土体会发生剪切破坏，土体形成重塑区，土体强度也随之改变。这种现象会导致土体重塑强度低于原土体强度，侧摩擦系数减小，因此桩土之间的静态摩阻力并不适用于桩侧摩阻力，需要计算桩土之间的动侧摩阻力。

Dover和Davidson[4]通过实验与分析认为，钢管桩在砂土中受到的动侧摩阻力可以将静侧摩阻力折减0.7到0.9倍得到；张海山等[10-12]认为沉桩过程中，大直街钢管桩内会形成10倍于桩径的土塞，桩壁内侧摩阻力是桩外侧摩阻力的50%。因此在考虑桩壁内侧摩阻力的基础上，对桩土之间的静态摩阻力使用折减因子进行折减，得到钢管桩在砂土层中的动侧摩阻力fs为：

fs=αkp0tanδ。

(3)

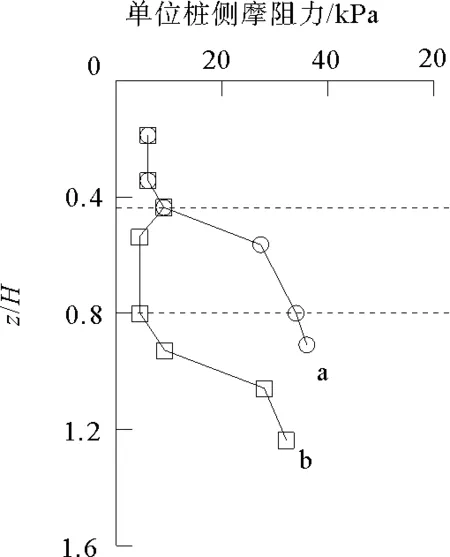
图2 单位侧摩阻的变化

式中：α为砂土动摩侧阻力折减系数，海洋岩土中α取0.75比较合理；k为地基压力系数；p0为土层上覆压力，kN；δ为土体外摩擦角。

对钢管桩在黏土层中桩侧摩阻力的计算，同样需要对土体强度进行折减。李飒等[13-15]通过分析与实验得出土体表面以下不同位置处的桩侧摩阻力受溜桩影响程度不同，将桩的入土深度划分为3个影响区，图2为不同影响区单位侧摩阻力的变化。

如图2所示，曲线a表示在溜桩结束时各深度处的单位侧摩阻力；曲线b表示了在打桩结束时各深度处的单位侧摩阻力，z为土体在泥面以下的深度，H为溜桩结束时的深度。根据土体在泥面以下的深度z与管桩溜桩结束时的深度H之间的比值，将管桩入泥土层分为完全影响区、不完全影响区和不影响区。

结合以上考虑，当钢管桩发生第一次溜桩时，桩动侧摩阻力可采用修正的API法来计算，计算公式为：

fd=0.3βcu。

(4)

式中：β为黏着系数，cu为不排水抗剪强度，kN/m2。当cu≥72 kPa时，β=0.5，当24 kPa≤cu<72 kPa时，β值在[0.5,1]区间内线性增加。

对于钢管桩发生二次溜桩的情况，计算桩在黏土层中的动侧摩阻力时，需要考虑第一次溜桩对桩侧摩阻力的影响，并根据影响程度的不同将桩基入泥深度区间分成三个影响区，分别是完全影响区、半完全影响区和无影响区。

1) 完全影响区

当z/H<0.5时，溜桩结束时的侧摩阻力与打桩结束时的侧摩阻力基本相同，且数值很小，这部分土体是受溜桩影响最为严重的区域，称其为完全影响区。将桩受到的动侧摩阻力通过折减成静摩侧阻力的0.075倍得到，计算公式为：

fd=0.075f。

(5)

式中：fd为黏土层中的动侧摩阻力，kN，f为静侧摩阻力，kN。

2) 半完全影响区

当0.50.44，即设计入泥深度较小，溜桩后，后续打桩距离设计入泥深度较小，后续打桩对土体性质影响较小，仍可采用修正的API法进行计算；②如果z/Hend<0.44即溜桩后，设计入泥深度较大时，后续打桩对土体性质影响较大，此时动侧摩阻力

fd=0.075f。

(6)

3) 无影响区

当z/H>0.8时，该区域溜桩对土体的扰动小，桩体侧摩阻力受溜桩的影响忽略不计，桩体动侧摩阻力仍可用修正的API法计算方法，则该区域侧摩阻力

f=0.3βcu。

(7)

式中：当cu≥72 kPa时，β=0.5；当24 kPa≤cu<72 kPa时，β值在[0.5,1]区间内线性增加。

3 溜桩区间计算方法

通过对溜桩机理的分析，针对现有的溜桩区间算法的计算过程进行了改进。首先采用别列柴策夫公式得到桩端阻力，再考虑溜桩对桩侧摩阻力的影响，将黏性土分成不同影响区并使用不同的折减因子计算摩阻力，砂质土中则通过常规方法计算桩侧摩阻力，并基于溜桩这一动态过程，采用静力平衡与功能原理建立大直径钢管桩溜桩区间的新计算方法。

当钢管桩贯入海洋土层中时，桩体会受到液压锤的锤击力、自身重力、浮力、桩端阻力及桩侧摩阻力的作用。根据动力学经验，在液压锤锤击管桩时，管桩与液压锤的动力视为1.2倍的桩与液压锤的重力之和(G1+G2)，所以管桩受力条件满足式(8)时会发生溜桩。通过式(8)～(9)即可计算出溜桩发生时管桩入泥深度L。

1.2(G1+G2)=f外+qu+F，

(8)

(9)

式中：F为管桩受到的浮力，kN；B为钢管桩直径，m；γs为海水的容重。

随着溜桩的进行，钢管桩的速度会在土阻力与浮力的作用下逐渐减小至零，即桩的动能在克服土阻力与浮力的做功中耗散，因此可根据功能原理列出能量方程，求出溜桩长度l。溜桩过程中桩侧摩阻力所做功的计算公式为:

(10)

式中：W1为桩侧摩阻力做的功，kJ；B为钢管桩直径，m；x为开始溜桩时的土层数；fmj为溜桩发生位置前第i层土的摩擦力，kN；y溜桩区间的土层数；fmj为溜桩区间内的第j层土的摩擦力，kN，v为桩在溜桩区间内的每层土中的滑动距离，m。

由积分学方法可得，fmj在溜桩区间为分段函数，故在溜桩区间内黏土层与砂土层的动摩擦阻力通过如下两式计算：

(11)

(12)

式中：fmd为溜桩区间内第j层黏土的摩擦力，kN；t为相应土层的厚度，m；fms为溜桩区间内第j层砂土的摩擦力，kN；pj-1为第j-1层土的上覆土压力，kN；γj为第j层砂土的重度，kN/m3；pj为第j层土的上覆土压力，kN。

对于溜桩过程中桩端阻力做的功，可通过对别列柴策夫公式积分得到，计算公式为：

(13)

式中：W2为桩端阻力做的功，kJ；t′为溜桩结束时钢管桩在所停留土层的插入长度，m。

钢管桩所受到浮力Ff会随着溜桩的进行逐渐增大，因此浮力所做的功

(14)

式中：ρ为水的密度，kg/m3；g为重力加速度，m/s2。

当液压锤对钢管桩进行锤击时，会有能量耗散，通常使用η系数进行修正，因此桩与锤在溜桩开始时具有的能量为ηE。综合以上考虑，根据能量守恒可得出桩的能量方程满足：

ηE=(G1+G2)l+W1+W2+W3。

(15)

根据式(15)即可求出溜桩长度l，结合溜桩发生时管桩入泥深度L，即可得到钢管桩的溜桩区间。

4 工程实例验算

根据南海荔湾桩基平台现场施工时采集的工程数据，选取合理的土体参数，使用新计算方法求出钢管桩的溜桩区间，将计算结果与实际工程中的溜桩区间进行比对分析，验证新计算方法的合理性。

该桩基平台共有16根钢管桩，平均分布在桩基平台的四个角上，每根钢管桩重643.9 kg，直径2.74 m，桩长为158 m。液压锤的型号为MHU1200S，额定输出能量1 200 kJ。为保证钢管桩周围土层性质相同，选取了平台一个角上的四根钢管桩进行计算分析。通过对土体参数分析可知，钢管桩所在土层软硬土层交替，土体浅层具有较长的黏土层，极易发生溜桩，并且在58.8 m和108 m的土体深度时，土体再次出现软黏土层，此时很大可能会发生二次溜桩乃至三次溜桩，钢管桩所在土层的土体参数列于表2。

结合实际工程选取的土体参数，使用式(1)～(7)计算得到钢管桩打桩过程中每层土的桩端阻力，砂土动侧摩阻力以及黏土的静摩擦阻力。由表2的计算结果可知，砂土层中桩体受到的桩端阻力较大，桩侧摩阻力较小，黏土层中桩端阻力较小，桩侧摩阻力较大，而在管桩刚贯入土层时，主要是通过桩端阻力承受桩与桩锤重力，由此也验证了溜桩产生的原因。

将表2的各土层阻力代入式(8)～(15)，求出溜桩发生时管桩的入泥深度与溜桩长度,得到了三个溜桩区间，分别为13.3～27 m、38.0～60 .5 m和64.9～84.0 m。通过理论溜桩区间与实际工程的溜桩区间的比对，得到了如图3所示的比对结果。

由比对结果可知，溜桩发生时桩的入泥深度及前两次溜桩区间与实际工程情况基本一致。对于第三次溜桩区间的计算有些偏差，这是由于第二次溜桩同样对土体产生了影响，使桩侧摩阻力发生变化，但第三次溜桩区间比理论计算的区间长度小，处于桩基工程安全范围内，故理论溜桩区间仍可为桩基设计提供参考。同时说明溜桩区间的计算需要考虑溜桩对土体产生的影响，新计算方法得到的溜桩区间与实际溜桩区间基本吻合，新计算方法的合理性得到验证。

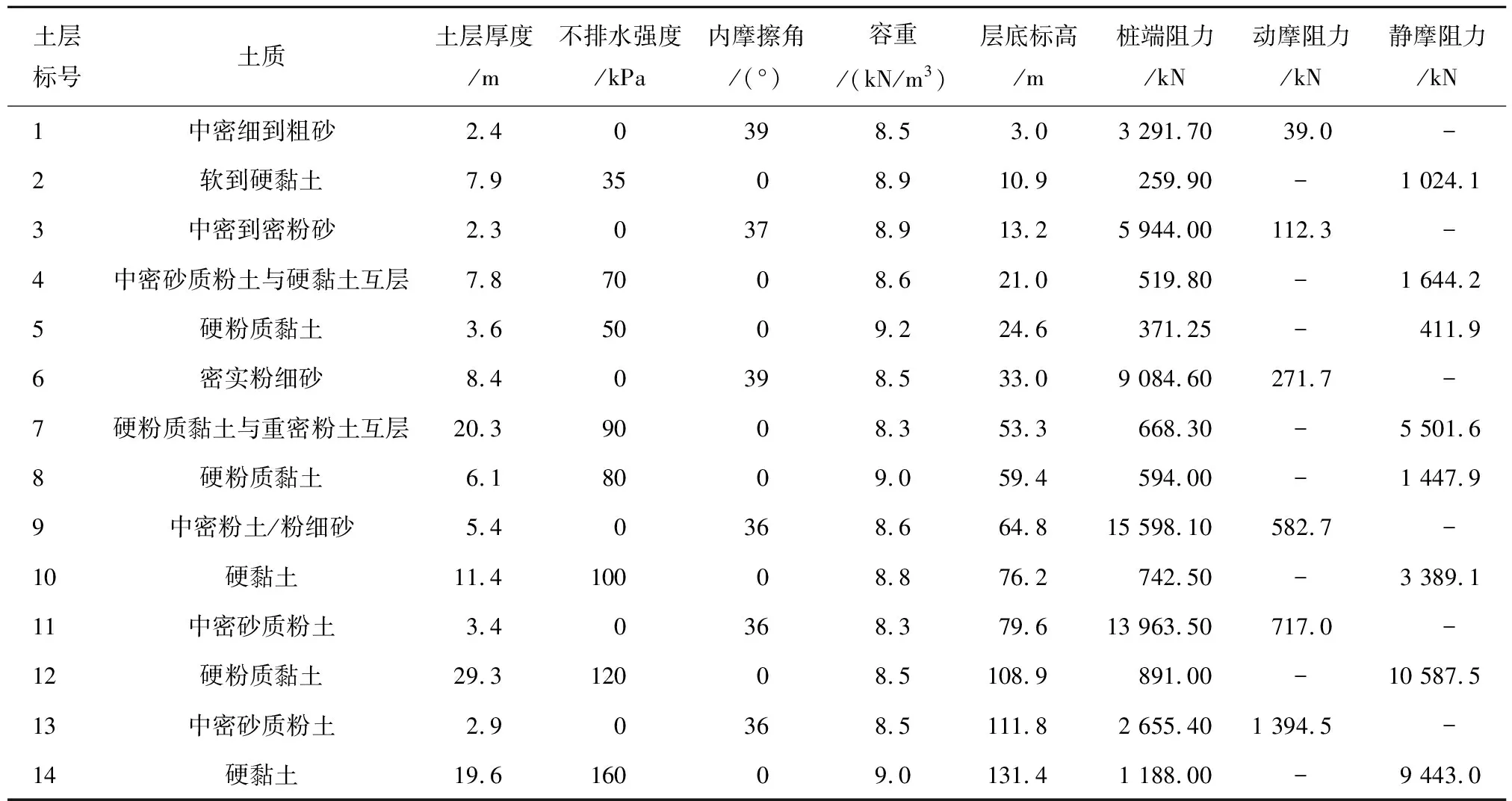
表2 各土层土体参数与土阻力计算结果

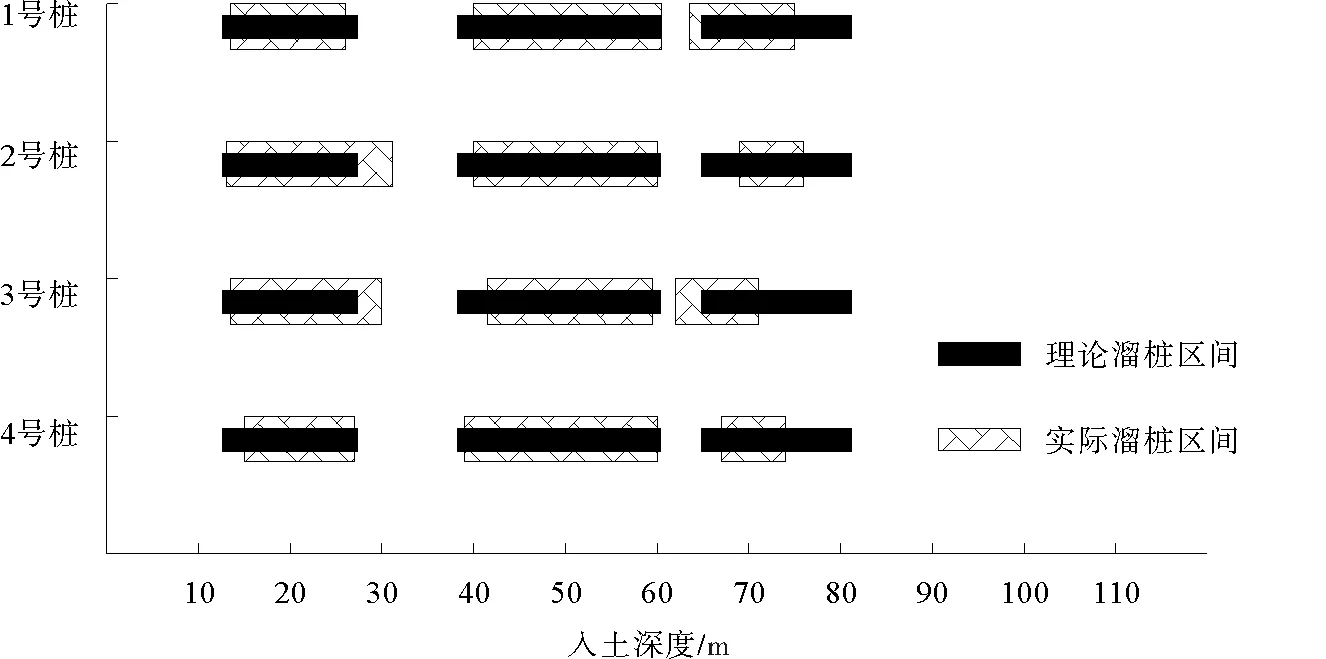
图3 理论溜桩区间与实际溜桩区间的比对

5 结论

通过对溜桩过程及产生原因的分析与研究，主要结论如下：

1) 当钢管桩发生二次溜桩时，考虑溜桩对桩侧摩阻力影响程度的不同，将黏土层中桩的侧摩阻力分为三个影响区，分别是完全影响区、半影响区和无影响区，对不同影响区的桩侧摩阻力使用不同的折减因子计算，新计算方法得到的溜桩区间更接近工程实际。

2) 计算钢管桩溜桩区间时，利用静力平衡原理，求出在溜桩开始时管桩的入泥深度，使用积分学方法列出不同影响区的桩侧摩阻力与桩端阻力所做功的表达式，再结合功能原理列出管桩的能量方程，即可求出溜桩长度，进而得出钢管桩溜桩区间。

3) 通过工程实例验核，新计算方法的第一、二次溜桩区间的计算结果与实际情况误差范围为8%～16%，具有较高的准确度；第三次结果虽有所偏差，理论溜桩区间小于实际溜桩区间，仍处于桩基工程安全范围内，仍可供海洋平台桩基设计及施工提供参考。