中考微专题复习课：值得重视的一类课型——以“特殊直角三角形再认识”复习课为例

☉江苏省江阴初级中学 陆 兵

进入中考复习阶段，涉及几何图形的习题往往与特殊直角三角形有关，而一类边长为“3，4，5”的特殊三角形更是经常见到.为了帮助学生深入理解这种三角形的相关性质，我们预设一节“特殊直角三角形的再认识”中考微专题复习课.本文梳理该课的教学流程，并跟进教学思考，供研讨.

一、“特殊直角三角形再认识”微专题复习课教学流程

活动1：从边长为“3，4，5”的三角形出发

问题：如图1，大家都很熟悉边长为“3，4，5”的三角形，你们想一想，这种形状的三角形有哪些特殊的性质？组内先交流一下，然后全班汇报.

预设：学生很快能确认这是一个直角三角形，如何证明？要引导学生概述一下勾股定理逆定理的证明思路.当然，如果学生的思路比较开阔，可能还会提及这种三角形的两个锐角的三角函数值可以求解出来，还有这种直角三角形斜边上的高为等等.在这个教学环节，重要的是引导学生全员思考，把目光聚焦到这种特殊三角形上来，为后续解题与研究起到“热身”作用.

活动2：例题求解与反思深入

例1如图2，有一张直角三角形纸片，两直角边BC=6，AC=8，点D在AC边上，现将△ABC沿直线BD折叠，使点C落在斜边AB上的点E处，求BD的长.

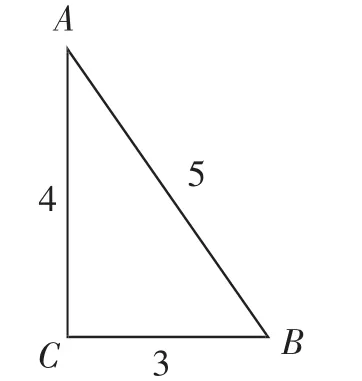
图1

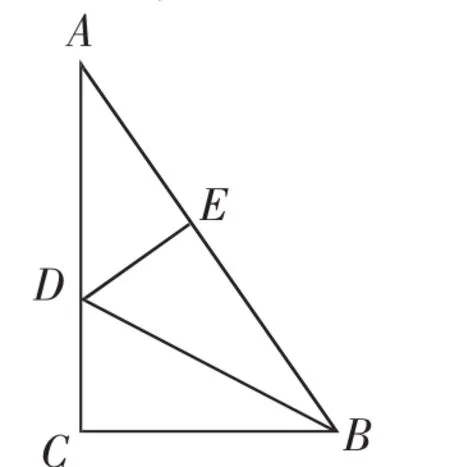
图2

教学预设：先安排学生独立探究，然后小组交流、全班展示、教师评析.学生根据翻折性质，想到设CD=DE=x，则AD=8-x.由BE=BC=6，可得AE=10-6=4，于是把目光投向直角三角形ADE，可利用勾股定理得关于x的方程：x2+42=（8-x）2，解得x=3，于是在直角三角形BCD中，求出BD=3

解后反思：为了避免“入宝山而空返”，让我们深入思考，进一步想清这个问题的结构，对于边长为“3，4，5”的直角三角形，边长4所对锐角的角平分线BD将对边分成两部分之比恰为3∶5，也就是图3中进一步还可得到特别是后者可以“一般化”，成为三角形角平分线的一个重要性质.再从锐角三角函数的角度看，图3中体现着一个重要性质：若tan2α=则tanα=反之也成立.

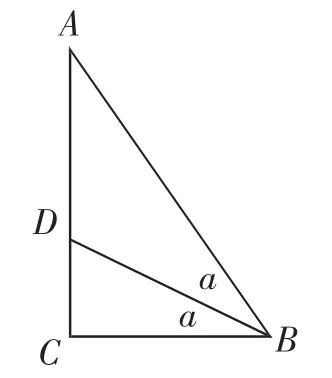
图3

成果扩大：研究了“3，4，5”直角三角形中一个较大锐角角平分线的性质，那么较小锐角角平分线有怎样类似的性质？

（安排学生独立探究3~5分钟）

变式思考：如图4，直角三角形ABC中，BC=3，AC=4，AE平分∠BAC，求证：AC=3CE.

学生可以模仿例1的思路，过点E作EF⊥AB于F，利用勾股定理构造方程求出CE的长，从而获得证明.

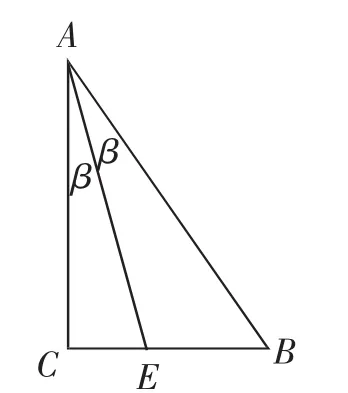
图4

在此基础上，引导学生“走向一般”，小结提炼出锐角三角函数的性质：若，则反之也成立.限于课堂时间，可安排学生课后进行演算证明.

多题归一：如图5，Rt△ABC中，BC=3，AC=4，角平分线AE、BD交于点G，求∠AGD的度数.

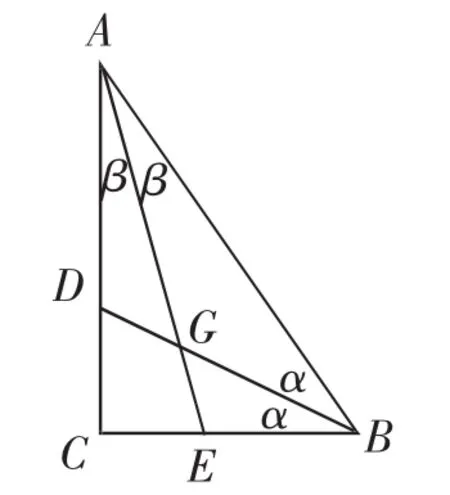
图5

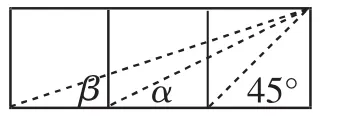
图6

思路预设：可以先利用图6来想清三角函数又一性质“当时，有tan（α+β）=1，即α+β=45°”，于是∠AGD为45°.

活动3：挑战高中“自招”考题

例2如图7，点E是正方形ABCD的边BC的延长线上一点，连接AE交CD于F，作∠AEG=∠AEB，EG交CD的延长线于点G，连接AG，当CE=BC=4时，作FH⊥AG于点G，连接DH，则DH的长为______.

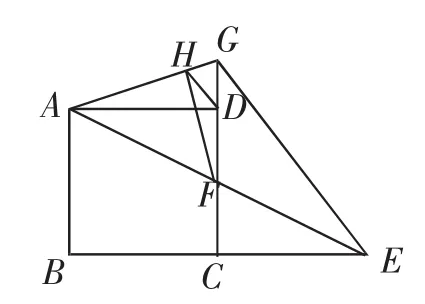
图7

思路预设：由上文例1深入反思后的一些经验积累，可得△CEG是“3，4，5”的直角三角形.可求得，相应的DG为于是可在Rt△ADG中求出；进一步识别出A、F、D、H四点共圆后可证△GDH △GAF.从而根据相似比易求得，所以

回顾反思：引导学生梳理概述本题的解题思路，并跟进追问哪几步是关键步骤，关键步骤是如何贯通思路的，以便强化学生对性质“若”的理解与运用.

例3 如图9，在平行四边形ABCD中，∠BAD=60°，点F是CD边上一点，将△ADF沿AF翻折，点D恰落在边BC上.当∠DAF=时的值为______.

思路预设：由例1反思得到的另一性质“若则可得到于是构造直角三角形AGE，确认该直角三角形是“3，4，5”直角三角形，于是再结合特殊直角三角形ABG（易求∠ABG=60°），可沟通AG、AB的关系为于是，即

图9

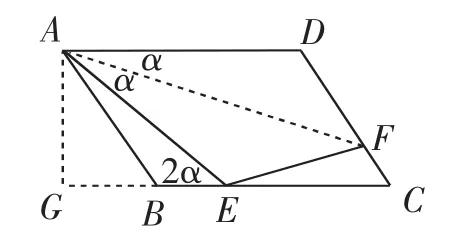
图10

活动4：课堂小结，布置作业

本课是对“3，4，5”直角三角形的再认识，特别是深化了这种三角形两条锐角角平分线带来的特殊性质，并从锐角三角函数的角度深刻理解它们.学生在小组内再互相交流一下学习心得，建议通过画出图形互相讲解一下对本课所学性质的理解.小组长可抽查组员对本课例题是否掌握，让组员讲解思路.

最后布置一道拓展题，供课后继续思考挑战.

拓展题：如图11，△ABC是⊙O（的内接三角形，AB=AC，点P是的中点，连接PA、PB、PC.若，求tan∠PAB的值.（提示：作BC边上的高AD，将问题转化为求tan∠DCQ的值）

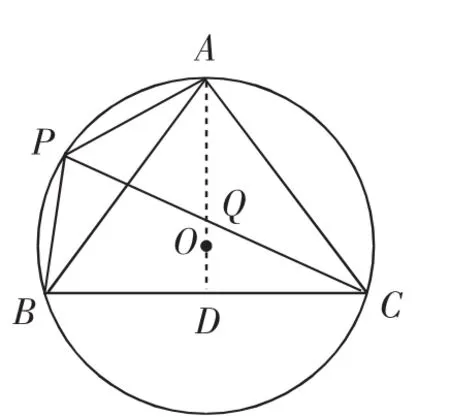
图11

二、教学思考

1.值得重视的微专题复习课型

当前初中一些刊物上出现一类新的教研视角，即倡导开展中考微专题的复习课型研究，并且出现了一些精彩的微专题课例，这些课例选定一个聚焦主题，选题围绕这个主题由浅及深，对一个图形或某个性质或某种解题策略进行了较有深度的研究，使得学生对这个专题达到了深刻理解的层次，是值得我们重视的.本文中的课例以特殊直角三角形为研究主题，重点关注的是边长为“3，4，5”的特殊直角三角形，也可看成一次微专题复习课型的实践研究.

2.较难题讲评要重视铺垫设问

中考复习期间，会有大量的较难试题，这类较难题如果就题讲题，核对答案，有时具有相同结构的较难题会过一段时间又出现一次，但是“零散”出现，学生容易遗忘，常常是题海中出现过的试题过一段时间又不会求解了.这时需要我们研发同一主题的微专题复习课，并对这些较难题预设铺垫式问题.事实上，本文课例的研究缘起主要是讲评例2、例3后发现效果不好，才想起可以借助微专题课型的启发，先预设一些铺垫式问题，像本文中的例1求解后深入思考，提炼、总结一些性质，并利用这些性质快速突破较难的例2、例3.在这个意义上说，教学即研究，解题教学即研究.