穷源竞流话最值，数形结合助析题——一道世界数学团体锦标赛试题引发的思考

☉浙江省台州市三门初级中学 李如军

一、源起

沙孟海先生在自传中提及自己一生的书法学习过程，他用四个字“穷源竞流”概括.今天我借沙先生的四个字与读者共话解题之道.笔者在翻阅某校九年级月考卷时，发现一道填空题得分率很高，过了几个星期之后笔者将此题作为简答题布置给学生再做，由统计结果得知得分率很低，我很诧异.在这高低变化过程中我和学生进行了简短的对话.

笔者：当初你是如何解决这道填空题的？

生：个人感觉应该是点E运动到中点的时候，此时F点是CD的中点.

笔者：为什么当E、F为各边的中点时，EF最小？当E为BC的中点时，F是否也为CD的中点？

这些问题一下子把该生难住了.

一道难度系数接近0.95的填空题，很容易被教师忽视.不再深入挖掘答对的习题是当下教学中普遍存在的问题.为了给学生更充足的时间，我将此简答题作为周末家庭作业，以期待更多更好的解答.

经历过这事以后，我开始反思自己的教学与解题.有很多得分率不低的题，作为教师的我们都想当然觉得学生已经掌握了，并且能上升到推理分析的角度完整解答，其实他们只是停留在主观臆测的层次.学生是否穷其源，谋其法，需要我们教师用“穷源竞流”加以引导，下面以一道几何题为例.

二、问题的提出

有这样一道考题：

试题（2017新昌期末卷）如图1，正方形ABCD的边长为2，点E、F分别在BC和CD上，∠EAF=45°，则EF的最小值是_______.

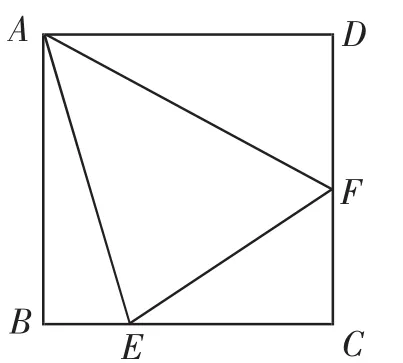
图1

三、竞流——解法欣赏

一部分学生看到这道题后采用直观想象的方法：在∠EAF不变的情况下，根据主观判断，E点从点B往点C运动的过程中，EF经历由大到小，再由小到大的过程，那么E、F关于直线AC对称时EF最短.即E、F分别为BC、CD的中点时，EF最小.其中有小部分学生脱离宏观分析，直接猜测E、F为BC的中点时，EF最小.（此法记为直观想象法，记为解法1）

在学习“旋转”一章后，有学生结合旋转的基本要素观察图形.这是一个正方形背景下的问题，想到将△ABE绕点A旋转至△ADE′，如图2.将一些变化分散的量集中到Rt△ECF中，利用勾股定理得到这是绝大部分学生反馈的周末作业，对于如何处理这个方程，很多学生束手无策.

图2

为什么用Δ法可以求得y的最值呢？有很多学生提出质疑.经过一些时间的讨论后，有学生给出了解释，如图3、图4.

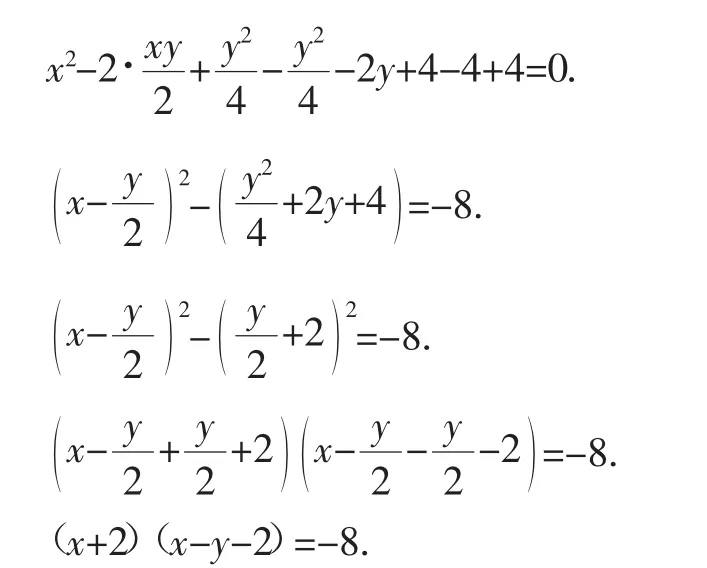
此时抛物线y1=（x+2）［x-（t+2）］必与y2=-8相交.

该生利用函数图像解释了参数y的最值问题，很直观，易于接受.此类方法是从方程的角度引入未知量x，借勾股定理建立方程，再结合二次函数与一元二次方程所学内容，把用函数图像解决方程问题演绎得淋漓尽致，同时把Δ法解释得很完美，我们着实为善于思考的学生拍手叫绝.（不妨记该法为解法2）

图5

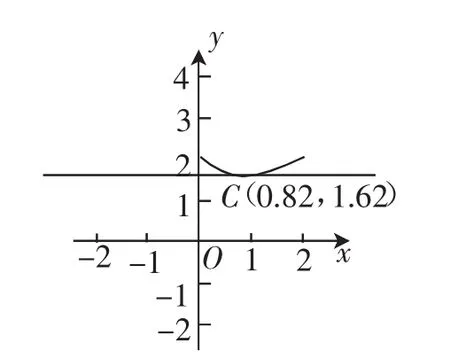
图6

笔者归纳：大家从最初的主观想象（猜测）到方程建模，函数图像的巧妙解析，从直观走向理性，从微观走向宏观.那么，能否从函数角度直接加以解决呢？经过笔者提示后，学生自然引入变量x与y，得函数关系式可惜此函数是初中阶段没有研究过的一类新函数，无论从表达式还是函数图像都很难得到它的函数值分布情况.故从函数角度研究其最小值是难以实现的.但是学过几何画板的学生还是绘制了草图（如图5）.从图像中不难看出，当x近似取0.84时，y最小，约为1.61（如图6）.尽管利用画板可以得到图像，但是难以精确，更何况平时没有条件使用.

至此，山重水复疑无路.笔者回顾解法2图形变换过程中有一个不变的量S△AEF=S△ABE+S△ADF，即 S△AEF=S△AE′F能否借助面积不变量分析法与算两次来实现呢？如图7，过点A作AB′⊥EF于点B′，交EF的平行线CG于点G，过C点作CC′⊥EF于点C′，设CC′=x，则AG=2+x，连接AC.由此可知

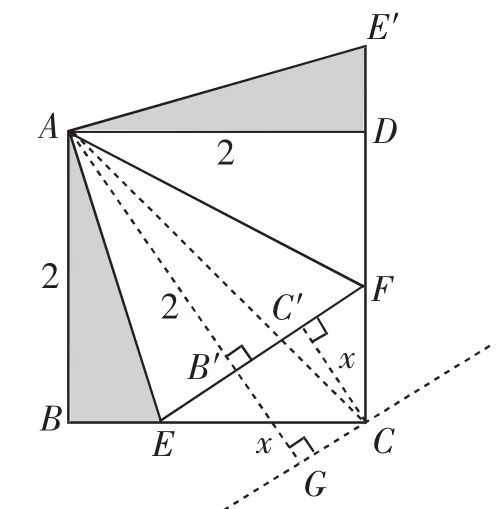
图7

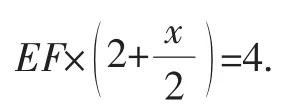
要使得EF最小，只要x最大.结合图形可知，AG≤AC，即

除了面积的倍数关系，很巧合的是题干中给我们的两个已知角也成倍数关系.从角度的倍数关系中是否可以再做做文章？在完成九上“圆”一章中“圆心角与圆周角”后，有学生提出这样的做法：因为∠EAF=45°不变，联想到圆中的圆周角，如图8，作△AEF的外接圆圆O，连接AO、EO、FO，作EF的中点M，连接OM、CM.易得OM⊥EF，CM=EM=MF.因为∠EAF=45°，所以∠EOF=90°.设圆的半径为r，所以所以由图可知，A、O、M、C四点共线，即时，r最小，此时则EF=也最小.（此法记为解法4）

图8

精彩的讨论交流完毕，有一位学生联想到曾经遇到的一道世界团体锦标赛试题.

（世界团体锦标赛试题）如图1，点E和F分别是正方形ABCD中，BC边和CD边上的点，且∠EAF=45°，求的最小值.

往常觉得很难的问题，如今变得简单了.此题解法此处不再赘述.至于新昌期末卷、团体锦标赛试题孰源孰流无从考证，抑或是一种巧合，经历这场讨论后，学生收获了这样的感受：难题无非是简单问题的叠加，只要穷源竞流多归纳，再难的问题也可以轻松解决.

四、解后反思

1.构造模型巧转化

解法3借助旋转知识，构造一对全等三角形，得到面积相等.把EF最小问题转化为线段AG最大问题，在解题过程中深切感受到面积法数形兼备，能把代数、方程中不变量分析法、算两次等思想方法融为一体.这种技法其实源于教材.“表示相等关系的式子叫等式”，这是教材中普通的话语，表现在数量上，我们通常要从不同的角度算两次，才能得到好的结果，人教版八下“勾股定理”的证明就是这种思想的美妙呈现.解法4是构造一个外接圆，把EF最小问题转化为折线段最短问题，即两点之间线段最短问题.此题的隐圆使用得非常漂亮.可以释放∠EAF=45°这个特殊的条件，只要0°＜∠EAF＜90°都可以通过此法解决.

当然，我们也可以通过构造方程模型、函数模型加以解决，只是主元法与新函数的研究貌似有点儿超纲，但是还是源于教材的.

2.数形结合妙解析

几何问题代数化就是数形结合最好的体现，无论是方程还是函数，都是代数化的表现形式，而参数方程最值问题（Δ法）处理过程中又离不开函数及其图像的支撑，华罗庚先生说得好“数缺形时少直观，形缺数时难入微”.解法1中暴露了“难入微”的尴尬.

3.宏观把控忆旧知

波利亚在《怎样解题》中指出：当问题比较困难时，我们可能很有必要进一步把问题再分解成几部分，并研究其更细微的末节.所以研究几何图形，一个基本方法就是教学中引导学生建立一个完整的知识网络，让学生的思维游走在一张四通八达的网上，教学中引导学生穷源竞流，相互交流碰撞出思维的火花，归纳出方法网，只有这样，解题的思维才能找到着力点，思维开阔，游刃有余.解得一法后归纳其法才能演绎出更多更好的问题解决之法.