V锥流量计用于气液两相流测量的数值模拟研究

张文康，钟兴林，朱亚斌，杨雪峰

（四川大学 化学工程学院，四川 成都 610065）

V锥流量计出现于20世纪80年代，其在保持孔板流量计测量精度高、稳定性高、可测多相流等优点的基础上，进行了改进，具有测量量程比宽、自整流、自清洁、压损小、所需直管段小等优点。

目前，国内外基于V锥流量计的气液两相流测量的研究已经取得了很大的进展:贺登辉等[1]针对湿气中液相流量在线检测误差较大的问题，提出采用V锥流量计压损比实现湿气液相流量直接测量的思路，并建立了湿气液相流量测量关联式；吴经伟[2]结合实验与仿真模拟得出了较为精确的内锥流量计可膨胀系数的拟合公式以及建立了测量湿气的经验公式；张福生[3]在正确识别流型的基础上，利用截面信息测量技术和V型内锥式流量计等传感器构成的多传感器融合系统进行了V锥流量计测量模型误差比较；胡俊等[4]针对水平管道中的气／水两相流，应用等效直径比β=0.65的V型内锥进行了实验研究，并应用基于流型修正的林宗虎关系式实现了气／水两相流测量，验证了采用V型内锥流量计测量气／液两相流的可行性。赵鹏[5]采用V型内锥流量计作为节流元件，将两相流信号的差压信号作为研究对象，实现了水平管道内两相流流型的识别；朱懿渊等[6]运用计算流体力学（CFD） 方法，对V锥流量计进行了数值模拟，得到了锥体上的压力和速度的详细分布情况；陈伟聪等[7]基于CFD多相流空化模型，对V锥流量计内流体的空化流动进行了数值计算；M.K.Sapra等[8]对不同节流比的V锥流量计进行了实验和CFD性能分析；R.K.Singh等[9]利用CFD研究了锥角和上游涡流对锥流量计性能影响。

由于目前国际上尚未对V锥流量计完成标准化，因此对V锥流量计的研究，特别是，其用于气液两相流测量的研究有重要意义。

1 物理模型与数学模型

1.1 几何模型和网格划分

V锥流量计是利用同轴安装在管道中的“V”形尖圆锥将流体逐渐地节流收缩到管道的内边壁，通过测量“V”形內锥体前后的差压来测量流量的。V锥流量计的几何结构如图1所示。管道直径D=50mm，节流装置等效直径比为0.75，V锥上、下游的直管段长度均取10D，取压点间距104mm。

由于V锥流量计的几何结构是轴对称的，因此可以采用二维数值模拟。利用ICEM CFD进行网格划分，如图2所示。整体采用四边形结构化网格，管道两端的网格相对稀疏，V锥处进行局部加密，网格总体数量为124789。

图1 V锥流量计结构简化图Fig.1 Simplified structure of V-cone flowmeter

图2 局部网格划分图Fig.2 Local meshing map

1.2 测量模型

在已有的研究中，更多的是采用孔板或文丘里流量计来测量气液两相流。测量模型主要有修正的Murdock关系式[10]、Chisholm关系式[11]、Smith＆Leang关系式[12]、De Leeuw 关系式[13]和林宗虎关系式[14]等。由于林宗虎关系式的形式简单灵活，所以本文研究的主要内容是将修正的林宗虎关系式推广至V锥流量计。

修正的林宗虎关系式的主要假设有:气液两相在流道中作分相流动，气相为不可压缩流体，气液两相的流量系数相同，在流动过程中不发生附加蒸发，气相的截面含气率不变，且当两相同时流过节流装置时作用在气相前后的压差和液相相同。如式 (1)所示:

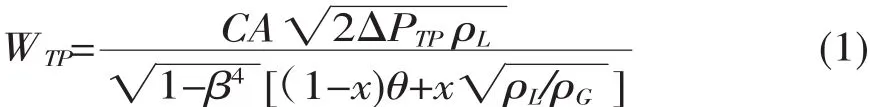
式中:WTP-总质量流量，kg/s；

C-V锥流量计的流出系数；

A-管道有效流通面积，m2；

△PTP-气液两相同时流经V锥时的压差，Pa；

ρL-液相密度，kg/m3；

ρG-气相密度，kg/m3；

β-V锥流量计的等效直径比；

x-干度；

θ-V锥流量计的修正系数。

1.3 模型参数设置

本研究采用Fluent进行数值模拟，采用压力基求解器，Mixture多相流模型，湍流模型采用RNGk-ε，近壁区域采用 Standard wall function，压力-速度耦合项采用SIMPLE算法，动量和湍动能项采用二阶迎风格式，体积分数项采用QUICK格式离散。边界条件采用质量进口和压力出口，湍流参数设置采用湍流强度和水力直径。

2 数值模拟结果分析

2.1 V锥流量计流场分析

图3和图4分别为气液密度比为0.00772、干度为0.3的两相流场的压力分布云图和与此两相流场相同质量流量的单相气体流场的压力分布云图。

图3 气液两相流场压力分布云图Fig.3 Pressure distribution nephogram of gas-liquid two-phase flow field

图4 单相气体流场压力分布云图Fig.4 Pressure distribution nephogram of single-phase gas flow field

对比图3和图4可知，在流经V锥节流件时，压力均急剧减小，其中两相流场在锥后0.0191m处减小到最小值，之后压力迅速升高，并在锥后0.157m处恢复至一定值；单相空气流场在锥后0.0158m处减小到最小值，之后压力迅速升高，并在锥后0.184m处恢复至一定值。当流场中有液相存在时，V锥节流件的上下游压差明显增大，造成此现象的原因可能是在流通截面存在液相，导致气相的流通截面积变小，从而气相的流速变快，即液相的存在对气相有加速作用，根据伯努利方程可知，气相流速的增加能导致节流件上下游的压差增大。另外，气液两相流的在锥后压力恢复所需要的直管段长度比单相空气在锥后压力恢复所需要的直管段长度要短，其原因可能是由于液相附着在管壁上，对管壁有一定的“润滑”效果，能够降低气相与管壁摩擦所带来的能量损失，因此气液两相流压力恢复所需要的直管段长度要更短。

图5为气液两相流场的流线图。从图5中看出，在V锥上游速度分布较为均匀，在经过V锥时，由于流通截面积的逐渐减小，所有流体开始集中到由壁面和V锥壁面所构成的狭小流通面中，并在流过流通截面积最小的地方后，在锥后形成了一个拉长的漩涡。根据边界层理论[15]，当黏性流体流经管道的进出口、阀门等流通截面积突然增大或减小的地方时，会出现边界层分离的现象，并且由于处于边界层内的流体与固体壁面分离产生倒流而形成漩涡。图6为气液密度比为0.00772，干度为0.3时的气相体积分数分布云图。从图6中看出，气相在流场上游分布较为均匀，但是在锥后一定位置处，气相开始集中，并在下游某一位置处又恢复均匀分布。造成这种气相在锥后“富集”的原因可能是液相由于气相的加速作用，惯性力较大而继续流向下游；而当流体流经流通截面积最小的地方时由于边界层分离，一部分气相倒流并在锥后形成漩涡，因此造成气相在锥后“富集”的现象。

图5 气液密度比为0.00772，干度为0.3时的流线图Fig.5 Streamline diagrams with gas-liquid density ratio of 0.00772 and dryness of 0.3

图6 气液密度比为0.00772，干度为0.3时的气相体积分数分布云图Fig.6 Vapor-liquid volume fraction distribution nephogram with gas-liquid density ratio of 0.00772 and dryness of 0.3

2.2 流出系数的标定

由于V锥流量计不是标准节流件，因此其流出系数需要重新标定。本文分别采用空气和水进行标定。而对于不可压缩流体，其流出系数可按式（2）进行计算确定:

式中:Wm-流体的质量流量，kg/s；

△P-节流装置两端的压差，Pa；

ρ-流体的密度，kg/m3；

d-V锥流量计的等效直径，m。

图7与图8为介质为空气和水时的流出系数随雷诺数的变化趋势图。由图7可知，空气的雷诺数大于150000时，C趋向稳定，其值为0.9；由图8看出，水在雷诺数大于200000时，C也趋向稳定，其值为0.88。本文标定V锥流量计的流出系数时，选择水和空气分别流经V锥流量计后得出的流出系数的平均值作为V锥流量计的流出系数，即C=0.89。

图7 空气流出系数与雷诺数关系图Fig.7 Reynolds Number Diagram of Air Outflow Coefficient

图8 水流出系数与雷诺数关系图Fig.8 Reynolds Number Diagram of Water Outflow Coefficient

2.3 V锥流量计修正系数的确定

林宗虎指出[16]，影响修正系数θ的最主要因素是气液密度比ρL/ρG，它是二相流动中的最主要的特征参数之一。因此，在一定的压力下，修正系数是气液密度比的函数。

根据修正的林宗虎关系式[16]的推导过程可知:

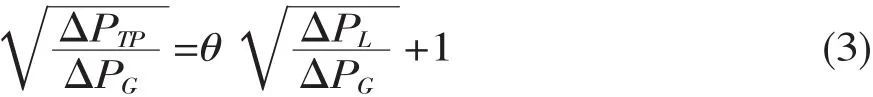
式中:△PG-气相单独流经V锥时的压差，Pa；

△PL-液相单独流经V锥时的压差，Pa。

本研究中，模拟条件均是在操作压强P=360000Pa下进行的。在同一密度比条件下，设置不同的气相流量和液相流量即可获得一组压差值，液相流量范围为:0.21～1.5kg/s，气相流量范围为:0.167～1.89kg/s。数据整理成Martinelli参数和的形式，并根据气液密度比的不同，将结果分别画于图中。图9和图10分别为气液密度比为0.0472和0.245时，和的关系。

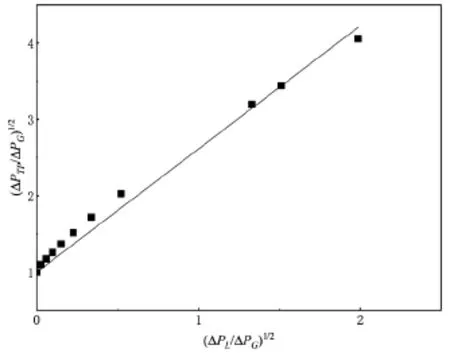
图9 气液密度比为0.0472时，与的关系Fig.9 The relationship betweenandwhen the gas-liquid density ratio is 0.0472

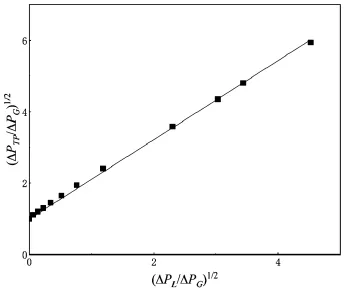
图10 气液密度比为0.245时，与的关系Fig.10 The relationship betweenandwhen the gas-liquid density ratio is 0.245

现将模拟得出的修正系数θ值及相应的值列于表1中，并按表1画出图11。

表1 修正系数θ及其相应的ρG/ρL值Tab.1 Correction Coefficient θ and Its Corresponding Value of ρG/ρL

图 11 θ=f(ρG/ρL)Fig.11 θ=f(ρG/ρL)

从图11中看出，θ值是随着气液密度比的变化而变化的，并在气液密度比达到0.328时，修正系数θ趋近于1。

图 12 不同 ρG/ρL时，和 （1-x） 的关系Fig.12 The relationship between and （1-x） at different ρG/ρL

3 结论

本文将修正的林宗虎关系式拓展至V锥流量计中，通过数值模拟得出了以下几点结论:

1） 直径为50mm，等效直径比β=0.75的V锥流量计的流场在锥前压力波动不大，在锥后压力波动较大的范围在锥后3D左右，因此安装所需要的后直管段长度至少为3D；

2） 当流体在直径为50mm，等效直径比β=0.75的V锥流量计的流动处于充分发展的湍流时，其流出系数可取值为0.89，且随着雷诺数的变化，流出系数趋于稳定；

3） 当V锥流量计用于测量气液两相流时，修正的林宗虎关系式中的修正系数θ值随气液密度比的增加而降低，在气液密度比大于0.328时，其值接近于1。另外，当流动介质的干度在0.1～1时，可通过查图12得出相应气液密度比下气液两相流的干度。