拉格朗日中值定理及其应用探析

李庆娟

（大连财经学院基础教育学院，辽宁大连116600）

1 预备知识和定理

拉格朗日中值定理又名有限增量定理或是拉氏定理，是法国著名数学家拉格朗日于1797年提出并加以证明的，因此命名为拉格朗日中值定理。拉格朗日中值定理是微分中值定理的核心内容，它是罗尔定理的直接推广，而柯西中值定理和泰勒中值定理又是拉格朗日中值定理在形式上及应用上的推广。拉格朗日中值定理是将函数与导数联系起来的一座桥梁，是研究函数的重要理论工具，它在微积分学中占有十分重要的地位，且有着广泛应用[1-2]。

定理1若函数f(x)满足：

（1）在闭区间[a,b]上连续；

（2）在开区间(a,b)内可导。

则在(a,b)内至少存在一点ξ，使得

f(b)-f(a)=f′(ξ)(b-a)。

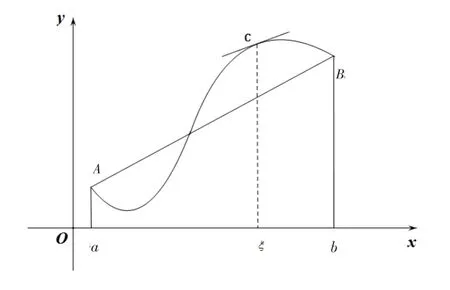
图1 拉格朗日中值定理

如图1，拉格朗日中值定理的几何意义是：如果连续曲线y=f(x)的弧AB上除端点外处处都有不垂直于x轴的切线，则在弧AB上至少存在一点C(ξ,f(ξ)) ，使得该点处切线平行于割线AB。

注：①定理中若a＞b，f(b)-f(a)=f′(ξ)(b-a)仍然成立，其中ξ介于a与b之间；

②定理的其它等价形式：

f(b)-f(a)=f′(a+θ(b-a))(b-a)，其中0＜θ＜1；

f(x+Δx)-f(x)=f′(x+θΔx) Δx，0＜θ＜1；

③从定理可以看出，由y=f(x)在某x处的取值或是性态，可进而判断x近旁处f(x)的取值和性态，这好像是一条关系链，对满足条件的[a,b]上f(x)全局有某种把控作用。

2 拉格朗日中值定理的应用

拉格朗日中值定理是微积分教学中的重要内容，掌握好定理以及应用，对学好微积分至关重要。拉格朗日中值定理不仅可以推导出微积分中的其它重要定理和公式，它还有着其它的重要应用，如求解函数极限问题、证明等式与不等式、讨论函数的性态、讨论方程根以及证明级数收敛的问题等等[3-4]。

2.1 在求解极限问题方面的应用

在微积分中求解函数极限的方法有很多种，基本方法有直接代入法、有理化法、重要极限法、夹逼定理法，比较典型的是洛必达法则、等价无穷小替换法，还有泰勒公式法等等，利用拉格朗日中值定理求解函数极限的方法虽然不常用，但也是一种比较的重要方法。

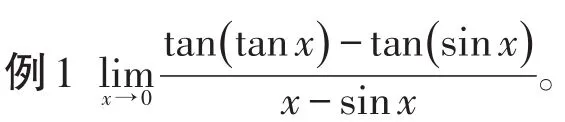
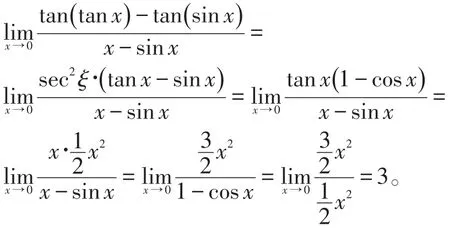
例2设 f(x)在[0 ,+∞ )上可导，且，试证明：x。

证明利用拉格朗日中值定理和极限定义式，再结合夹逼定理进行处理。

设x0＞0（足够大），在区间[x0,x]上应用拉格朗日中值定理得，

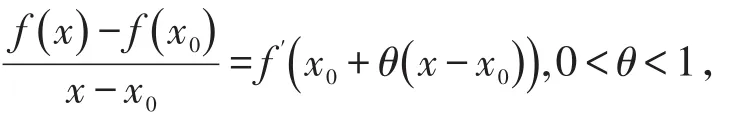
对所求极限式子进行处理

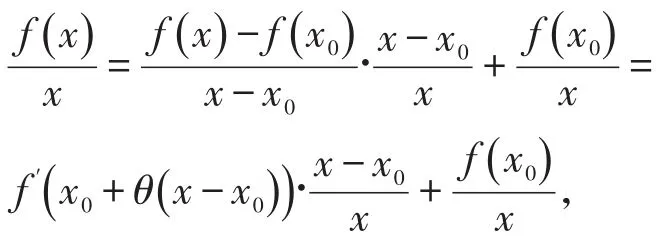
再由三角不等式可得

当x→+∞时，同时x0+θ(x -x0)→+∞，

故不等式右端极限为零，由夹逼定理

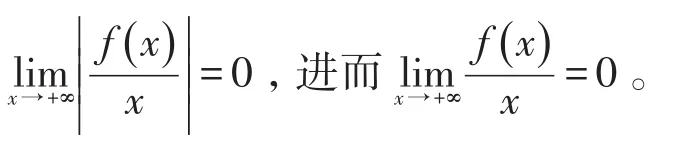
2.2 在证明不等式问题中的应用

利用拉格朗日中值定理证明不等式也是高等数学教学中证明不等式的一种典型方法，通过构造辅助函数，利用拉格朗日中值定理，对式子进行放缩或是再结合单调性进行证明。

例3设e＜a＜b＜e2，证明

证明构造辅助函数，令 f(x)=ln2x,显然函数f(x)满足在[a ,b]上连续，在(a ,b)内可导，由拉格朗日中值定理可得至少存在一点ξ∈(a ,b)，使得

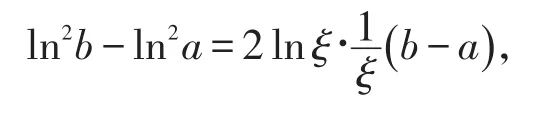
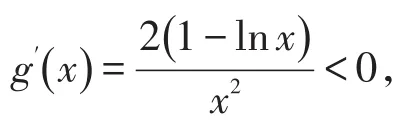
注意：此题也可以直接用单调性证明，可令

例4设非负二阶可微函数 f(x)在[0 ，+∞ )内满 足 f″(x)＞0，对 常 熟 a＞0，证明：

证明利用变限法构造辅助函数，令

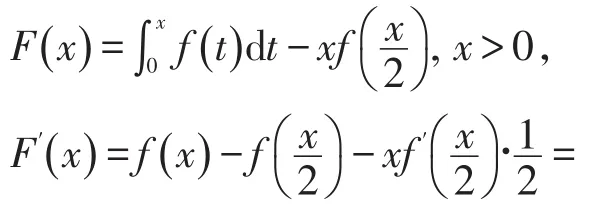
（利用拉格朗日中值定理进行处理）

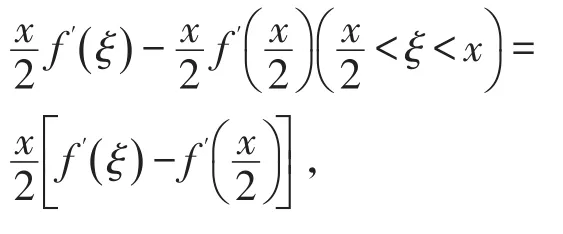
因 为 f(x)在[0 ,+∞ )内 满 足 f″(x)＞0，所 以，故F(x)在[0 ,+∞ )内单调递增，进而F(a)＞F(0)=0，即得证。

2.3 在证明等式问题中的应用

利用拉格朗日中值定理证明等式问题是拉格朗日中值定理内容的一个直接应用，当被证的结论中含有 f(a),f(b),ξ,f′(ξ)等时，我们往往考虑用拉格朗日中值定理证明。

例5设 f(x)在闭区间[a ,b]上连续，在开区间(a ,b)内可导，证明：在(a ,b)内至少存在一点 ξ，使得

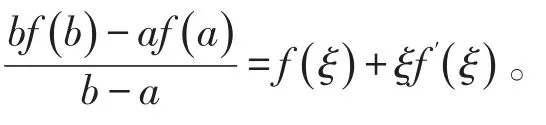
证明从形式上来看是拉格朗日中值定理的应用。

构造辅助函数，令F(x)=xf(x)，函数在[a ,b]上显然满足拉氏定理条件，从而至少存在一点ξ，使得，即ξf′(ξ)得证。

2.4 在讨论函数的性质方面的应用

微分中值定理为研究函数的性态提供了重要的理论工具，拉格朗日中值定理作为微分中值定理的核心内容更是如此。

例6证明函数 f(x)在有穷区间(a ,b)内可微分，但无界，则其导函数 f′(x)在区间(a ,b)也无界。

证明采用反证法和拉格朗日中值定理

假设 f′(x)在区间(a ,b)有界，即存在M＞0，使得

对于任意a＜c＜x＜b，f(x)在区间[c ,x]上满足拉格朗日中值定理条件，所以

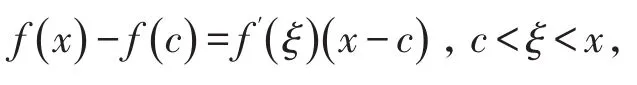
进而

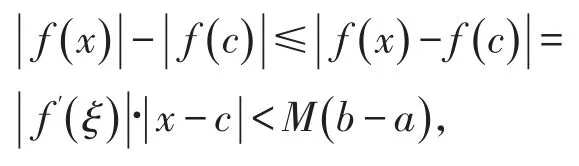
故| f(x)|＜M(b -a)+| f(c)|，这显然与函数 f(x)在有穷区间(a ,b)内无界矛盾，所以假设不成立，即f′(x)在区间(a ,b)也无界。

例7设函数 f(x)在开区间(- ∞,+∞ )内有有界的导函数，则函数 f(x)在(- ∞,+∞) 内一致连续。

证明对任意x1,x2∈(- ∞,+∞ )，由拉格朗日中值定理可得

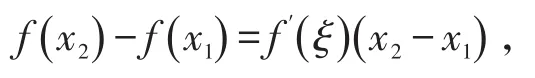
其中ξ介于x1与x2之间，由已知条件 f(x)的导函数有界，故存在M＞0，使得| f′(ξ)|＜M，所以，∀ε＞0 取时，有

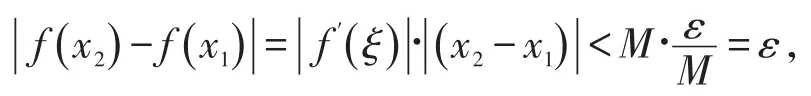
从而可知函数 f(x)在(- ∞,+∞ )内一致连续。

2.5 在方程根的讨论问题中的应用

对于方程根讨论问题，经常利用的方法就是零点存在定理、介值定理、单调性判定定理等，而拉格朗日中值定理也会在某些方程根的讨论时起着重要作用。

例8设函数 f(x)在[a ,+∞ )内连续，在(a ,+∞)内 可 导 ， f′(x)＞k＞0，其 中 k为实 数 ，又 已知f(a)＜0，证明 f(x)=0在区间内有且仅有一个实数根。

分析：主要思想是利用零点存在定理进行判断，但如何确定右端点的正负呢？借助于拉格朗日中值定理。

证明首先设，也就是证 f(x)=0在区间(a ,b)内有且仅有一个实数根。由已知条件可知f(x)满足在[a ,b]上连续，在(a ,b)内可导，由拉格朗日中值定理可得至少存在一点ξ∈(a ,b)，使得 f(b)-f(a)=f′(ξ)(b -a)，进而得

又因为 f(a)＜0，由零点存在定理，f(x)=0在区间(a ,b)内至少有一个实数根，再由 f′(x)＞k＞0可知，函数单调递增，故 f(x)=0在区间(a ,b)内有且仅有一个实数根，命题得证。

例9设函数 f(x)在[a ,+∞ )上有二阶导数，且满足f(a)=A ＞ 0,f′(a )＜0，当 x∈(a ,+∞ )时，f″(x)＜0，证明：f(x)在(a ,+∞ )内恰有一个零点。

证明首先讨论 f(x)在(a ,+∞ )的单调性，对于任意 x∈(a ,+∞ )，对 f′(x)在[a ,x]上应用拉格朗日中值定理，可得 f′(x)-f′(a)=f″(ξ)(x -a )，ξ∈(a ,x)由已知条件进而可得 f′(x)＜0，所以 f(x)在(a ,+∞)内单调递减。对 f(x)在[a ,x]上再次应用拉格朗日中值定理，可得

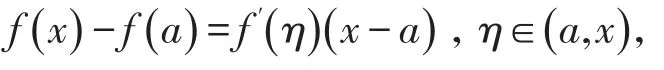
即

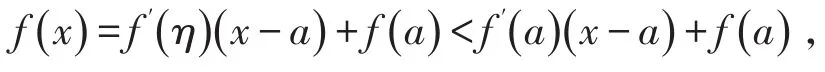
因为f(a)=A ＞ 0,f′(a)＜0，当x→+∞，上述不等式右端趋于负无穷，即 f(x)能取到负值，不妨设，则当x＞x时，必有 f(x)＜0，所以0对于任意x∈(x0,+∞ )，由零点存在定理，f(x)在[a ,x]至少有一个零点，又因为 f(x)在(a ,+∞ )内单调递减，所以 f(x)在(a ,+∞ )内恰有一个零点。

2.6 在级数收敛证明中应用

例10已知正项级数发散，部分和序列sn=u1+u2+…un，证明：级数收敛。

证明首先构造辅助函数α＞0，函数连续且可导，当 n＞2时，在闭区间[sn-1,sn]上，函数 f(x)均满足拉氏定理条件，故至少存在一点ξn,(sn-1＜ξn＜sn)，使得

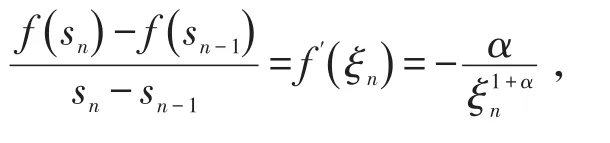
而

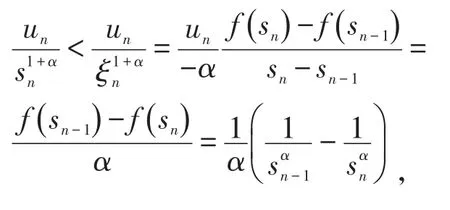
3 结语

综上所述可知拉格朗日中值定理的重要性，它不仅是微分中值定理的重要的组成部分，它的应用更是广泛，介绍了拉格朗日中值定理的六大主要应用，事实上，它还有很多应用等待进一步去研究。