Hermite-Hadamard Type Inequalities for Operator h-preinvex Functions
Lian Tie-yanand Tang Wei
(1.College of Arts and Sciences,Shaanxi University of Science and Technology,Xi’an,710021)
(2.College of Electrical and Information Engineering,Shaanxi University of Science and Technology,Xi’an,710021)
Communicated by Ji You-qing
Abstract:Operator h-preinvex functions are introduced and a re finement of Hermite-Hadamard type inequalities for such functions is established.Results proved in this paper are more general and some known results are special cases.
Key words:Hermite-Hadamard’s integral inequality,operator h-preinvex function,operator beta-preinvex function
1 Introduction
Let I,J be intervals in R,(0,1)⊆J.Let B(H)be the algebra of all bounded linear operators on a complex separable Hilbert space H.Denoted by B(H)adthe set of selfadjoint operator in B(H).In 1991,Pe˘ccari´c et al.[1]proved the following integral inequality:
Let f:I⊆R→R be a convex function and a,b∈I with a which is known as the Hermite-Hadamard’s integral inequality. More recently,a number of papers have been written providing noteworthy extensions,generalizations and re finements for more extensive functions(see[2]–[15]). Sarikaya et al.[15]introduced a new class of convex functions called h-convex functions,and proved the following Hermite-Hadamard type inequalities for h−convex functions. Definition 1.1[15]Let h:J→R be a non-negative function.We say that f:I⊆R→R is an h-convex function,if f is nonnegative and for all x,y∈I and t∈(0,1),we have If the above inequality is reversed,then f is said to be h-concave. This notion unifies and generalizes the known classes of functions,for instance,convex functions,s-convex functions in the second sense,Gudunova-Levin functions and P-functions,which are obtained by putting in(1.2), respectively.Many properties of functions mentioned above can be found in[12]–[14]. Theorem 1.1[15]Let h:J→R be a non-negative function with.If f is h-convex with f∈L1[a,b],then Hason[16]gave the notion of invexity as significant generalization of classical convexity.Let X be a real vector space.A set S⊆X is said to be invex with respect to the map η:S×S→X,if for every x,y∈S and t∈[0,1], It is obvious that every convex set is invex with respect to the map η(y,x)=y − x,but there exist invex sets which are not convex(see[17]). For every x,y ∈ S the η-path Pxvjoining the points x and v:=x+η(y,x)is defined as The mapping η is said to be satisfies the condition(C)if for every x,y ∈ S and t∈ [0,1], Note that for every x,y ∈ S and t∈ [0,1],if η satisfying condition(C)we have In fact, Definition 1.2[11]Let h:J→R be a non-negative function,and let K be an invex set of Rnwith respect to η(·,·).We say that f:K → R is an h-preinvex function with respect to η(·,·),if f is nonnegative and for all x,y ∈ K and t∈ (0,1),we have If the above inequality is reversed,then f is said to be h-preconcave. Many classes of functions can be treated on unified way by h-preinvex functions.If and we have the definition of preinvex function,the definition of s-preinvex function,the definition of Q-preinvex function,the definition of P-preinvex function,and the definition of beta-preinvex function on K,respectively.In fact,the concept of beta-preinvex functions on I introduced by Noor et al.[5]are quite general and unifying ones. In[5],some Hermite-Hadamard’s integral inequalities were established for beta-preinvex functions,and their results can be viewed as significant and important generalizations of several previously known results. Theorem 1.2[5]Suppose that f:I=[a,a+η(b,a)]⊆R→R is a beta-preinvex function with a In[7],Ghazanfari introduced the definition of operator s-convex function and established some Hermite-Hadamard type inequalities in which some operator s-convex functions of selfadjoint operators in Hilbert spaces were involved. Definition 1.3[7]Let I be an interval in[0,∞)and K be a convex subset of B(H)ad.A continuous function f:K→R is said to be operator s-convex on I for operators in K if in the operator order in B(H),for all λ∈[0,1]and for every positive operators A and B in K whose spectra are contained in I and for some fixed s∈(0,1]. Theorem 1.3[7]Let f→R be an operator s-convex function on the interval I⊆[0,∞)for operators in K⊆B(H)ad.Then for all positive operators A and B in K with spectra in I we have the inequality In this paper,we introduce operator h-preinvex functions,and a re finement of Hermite-Hadamard type inequalities for operator h-preinvex functions is established.As corollaries,the above Theorem 1.3 is generalized for operator h-preinvex functions,and Theorem 1.2 is proved to be true for operator beta-preinvex functions. Definition 2.1 Let h:J→R be a non-negative function and S⊆B(H)sabe an invex set with respect to η:S×S → B(H)sa.A continuous function f:I→ R is said to be operator h-preinvex on I with respect to η for operators in S if for the operator order in B(H),for t∈(0,1)and for every A,B∈S whose spectra are contained in I.If the above inequality is reversed,then f is said to be operator h-preconcave. We can discuss some special cases of operator h-preinvex function. If h(t)=tp(1−t)q,then we have the definition of operator beta-preinvex functions. Definition 2.2 Let I be an interval in R and S⊆B(H)sabe an invex set with respect to η:S×S→B(H)sa.For some p,q> −1,a continuous function f:I→R is said to be operator beta-preinvex on I with respect to η for operators in S if for the operator order in B(H),for t∈(0,1)and for every A,B∈S whose spectra are contained in I. Remark 2.1 In view of Definition 2.2,a function is said to be operator beta-convex with respect to the map η(B,A)=B − A,operator tgs-preinvex by letting p=q=1 and operator P-convex with η(B,A)=B − A,p=q=0. If p=s,q=0,or p=1,q=0,then the Definition 2.2 reduces to: Definition 2.3 Let I be an interval in R and S⊆B(H)sabe an invex set with respect to η:S×S→B(H)sa.For some fixed s∈(0,1],a continuous function f:I→R is said to be operator s-preinvex on I with respect to η for operators in S if and a continuous function f:I → R is said to be operator preinvex on I with respect to η for operators in S if for the operator order in B(H),for all t∈(0,1)and for every A,B∈S whose spectra are contained in I. Every operator convex function is an operator preinvex with respect to the map η(B,A)=B−A,but the converse does not hold. Proposition 2.1 Let I be an interval in R,S⊆B(H)saan invex set with respect to η:S×S → B(H)saand η satisfies condition(C)on S and f:I→ R is a continuous function.Then for every A,B ∈S with spectra of A,V:=A+η(B,A)in I,the function f is operator h-preinvex on I with respect to η for operators in η-path PAVif and only if the function φx,A,B:[0,1]→ R defined by is h-convex on[0,1]for every x∈ H with∥x∥=1. Proof. Let the function f be operator h-preinvex on I with respect to η for operators in η-path PAV.Suppose that A,B ∈S with spectra A,V in I.Since therefore,for any t∈[0,1], If t1,t2∈ [0,1],since η satisfies condition(C)on S,we have for every λ ∈ [0,1]and x ∈ H with ∥x∥=1.Therefore,φx,A,Bis h-convex on[0,1]. Conversely,suppose that x ∈ H with ∥x∥ =1 and φx,A,Bis h-convex on[0,1].Let C1:=A+t1η(B,A),C2:=A+t2η(B,A)∈ PAV.Fix λ ∈ [0,1],by using(1.4)we have Hence f is operator h-preinvex with respect to η for operators in η-path PAV. Using the technique of Ghazanfari and Barani[9],we establish a generalization of Hermite-Hadamard inequality for operator h-preinvex functions. Theorem 3.1 Let h:J⊆R→R([0,1]⊆J)be a non-negative function.Let I be an interval in R,S ⊆ B(H)sabe an invex set with respect to η:S × S → B(H)saand η satisfies condition(C)on S.If for every A,B ∈S with spectra of A,V:=A+η(B,A)in I,f:I → R is operator h-preinvex on I with respect to η for operators in η-path PAV,h(t)≤ t andfor t∈[0,1],then the following inequalities holds for k is a positive integer: If f:I → R is operator h-concave on I with respect to η for operators in η-path PAV,h(t)≥t andfor t∈[0,1],then the reverse inequalities hold in(3.1). Proof. Since f is operator h-preinvex on I with respect to η and the result of Proposition 2.1 has been established,utilizing(1.3),the following Hermite-Hadamard inequality hold for real-valued h-convex function φ on the interval Summation of the above inequalities over i=0,1,···,k − 1 yields Hence Since η satisfied condition(C),therefore by(1.4)for t∈ [0,1]we have Summation of the above inequalities over i=0,1,···,k − 1 and the following equality yields Combining inequalities(3.4)and(3.6),we obtain the first three inequalities of(3.1). Moreover,by using the h-preinvexity of f and h(t)≤t for t∈[0,1],we have It is easy to get the last inequality of(3.1)by multiplying the above inequality with the appropriate coefficient. Similar to the proof of Theorem 1.1 in[15],it is obvious that both the inequalities(1.3)hold in reversed direction if f is h-concave.Then using h(t)≥t,we obtain the desired result. Remark 3.1 Suppose that f:I → R is operator h-preinvex on I with respect to η for operators in η-path PAV,and without the condition of h(t) ≤ t,then the first three inequalities of(3.1)hold.Conversely,if f:I→R is operator h-preconcave on I with respect to η for operators in η-path PAV,and without the condition of h(t) ≥ t,the first three inequalities of(3.1)are reversed. Corollary 3.1 Let I be an interval in R,S⊆B(H)sabe an invex set with respect to η:S×S→B(H)saand η satisfies condition(C)on S.If for every A,B ∈S with spectra of A,V:=A+η(B,A)in I,f:I → R is operator beta-preinvex on I with respect to η for operators in η-path PAVand k is positive integer,p,q≥ −1 with tp(1−t)q≤ t for t∈ [0,1],then the following inequalities hold: Proof. Since f is operator beta-preinvex,we obtain(3.7)by taking h(t)=tp(1−t)qin(3.1). Corollary 3.2 Let I be an interval in R,S⊆B(H)sabe an invex set with respect to η:S×S→B(H)saand η satisfies condition(C)on S.If for every A,B∈S with spectra of A,V:=A+ η(B,A)in I,f:I → R is operator s-preconcave on I with respect to η for operators in η-path PAV,where s ∈ (0,1),then Proof. Since f is operator s-preconcave,by the conclusion of Theorem 3.1,taking h(t)=ts,then we get the desired inequality. Since every operator convex function is operator h-preinvex with respect to the map η(B,A)=B −A and h(t)=t,Theorem 3.1 generalizes the following result which was obtained in[8]. Corollary 3.3[8]Let f:I→R be an operator convex function on the interval I.Then for any selfadjoint operators A and B with spectra in I,we have the inequality: Corollary 3.4[9]Let I be an interval in R,S⊆B(H)sabe an invex set with respect to η:S×S→B(H)saand η satisfies condition(C)on S.If for every A,B ∈S with spectra of A,V:=A+η(B,A)in I,f:I → R is operator preinvex on I with respect to η for operators in η-path PAV,then Corollary 3.5 Let I be an interval in R,S⊆B(H)sabe an invex set with respect to η:S×S →B(H)saand η satisfies condition(C)on S.If for every A,B ∈S with spectra of A,V:=A+η(B,A)in I,f:I → R is operator preinvex on I with respect to η for operators in η-path PAV,then Proof. Since f is operator preinvex on I with respect to η for operators in η-path PAV, is convex on[0,1]by Proposition 2.1.If the above inequality(3.9)in numerical form with η(y,x)=y − x for x,y ∈ I hold for real-valued convex function φx,A,Bon[0,1],then a simple consequence is the integral,which is closer to the left bound than to the right: Therefore,we get the desired inequality. Remark 3.2 Suppose that f:I=[a,a+η(b,a)]⊆R→R is a beta-preinvex function with a Remark 3.3 By the Remark 3.1,we get(1.6)proved in[7]by letting k=2,η(B,A)=B−A in(3.8). Corollary 3.6 Let I be an interval in R,S⊆B(H)sabe an invex set with respect to η:S×S→B(H)saand η satisfies condition(C)on S.If for every A,B ∈S with spectra of A,V:=A+ η(B,A)in I,f is operator tgs-preinvex function on I with respect to η for operators in η-path PAV,then Theorem 3.2 If for every A,B ∈S with spectra of A,V:=A+η(B,A)in I,f:I→R is operator h-convex on I with respect to η for operators in η-path PAV,then f is non-negative for every A∈S withand f is non-positive for every A∈S with Proof.For A∈S,we have Corollary 3.7 If f is operator beta-convex on[0,∞]for operators in S which is an invex set of B(H)sa,then f is non-negative for every A∈S with p+q≤1 and f is non-positive for every A∈S with p+q≥1. Proof. Since f is operator beta-convex,we observe that Then by Theorem 3.2,we obtain the desired result. Corollary 3.8 If f is operator beta-concave on[0,∞]for operators in S which is an invex set of B(H)sa,then f is non-positive for every A∈S with p+q≤1 and f is non-negative for every A∈S with p+q≥1. Remark 3.4 By Theorem 3.2 and Corollary 3.7,it’s easy to see that if f is operator s-convex functions or operator P-convex function on[0,∞]for operators in S which is an invex set of B(H)sa,then f is non-negative for every A∈S.But there is an opposite result for operator tgs-convex function,and for operator s-concave functions. Theorem 3.3 Let I be an interval in R,S ⊆ B(H)saan invex set with respect to η:S×S → B(H)saand η satisfies condition(C)on S.If for every A,B ∈ S with spectra of A,V:=A+η(B,A)in I,f:I → R is operator s-preinvex on I with respect to η for operators in η-path PAVwith spectra of A and V in I,then for every a,b ∈ (0,1)with a1,0≤m≤r: Proof. Firstly,we define the function By the continuity of function f,the continuity property of the inner product and the properties of the integral of operator-valued functions,we have Since f(A+lη(B,A))≥ 0,we know that φ(t)≥ 0 for all t∈ I and Secondly,since f is operator preinvex on I with respect to η for operators in η-path PAV,by using Proposition 2.1 with h(t)=ts,we have the function φ′(t)is s-convex.Thus,applying Corollary 3.1 in[10],we have Finally,function substitutions deduce(3.11)holds. Corollary 3.9 Let I be an interval in R,S⊆B(H)saan invex set with respect to η:S×S→B(H)saand η satisfies condition(C)on S.If for every A,B∈S with spectra of A,V:=A+η(B,A)in I,f:I → R is operator preinvex on I with respect to η for operators in η-path PAVwith spectra of A and V in I,then for every a,b ∈ (0,1)with a Proof. Since f is operator preinvex on I with respect to η for operators in η-path PAV,we obtain(3.12)by using Theorem 3.3 with s=1,r=2,m=1. Corollary 3.10[9]Suppose that all the assumptions of Corollary 3.9 are satisfied.Then for every a,b∈(0,1)with a Proof. Since f is operator preinvex on I with respect to η for operators in η-path PAV,then we obtain(3.13)by using Theorem 3.3 with s=1,r=m=1.














2 Some New Concepts of Operator h-preinvex Functions and Its Variant Form









3 Hermite-Hadamard Type Inequalities










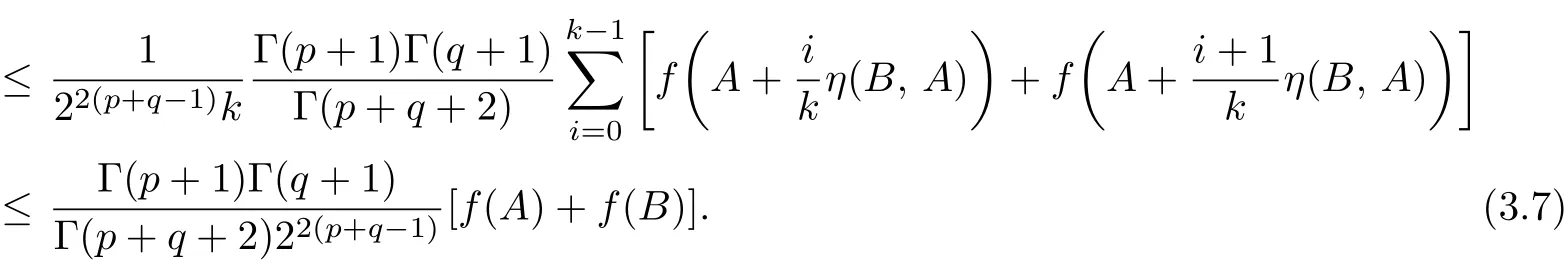





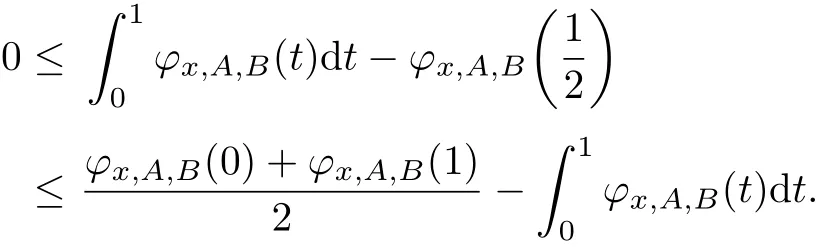


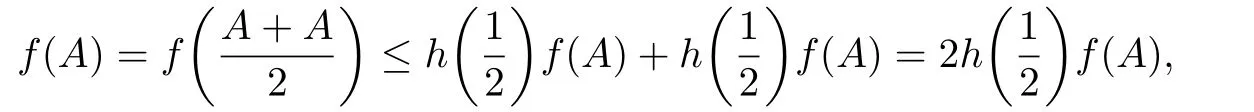






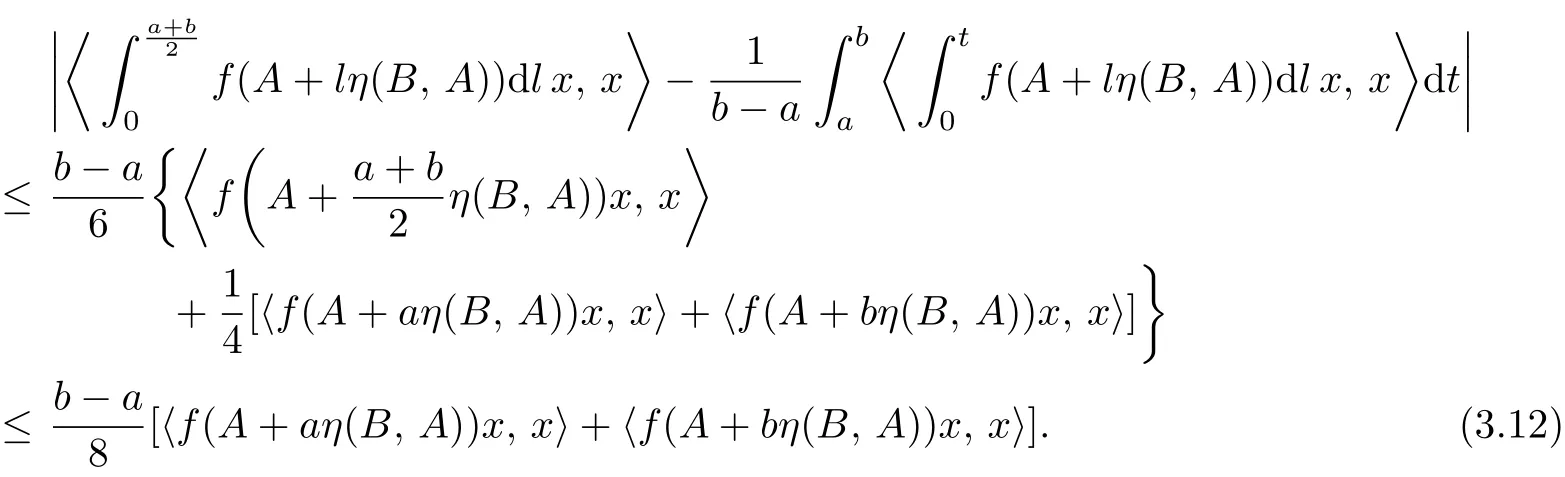

 Communications in Mathematical Research2019年2期
Communications in Mathematical Research2019年2期
