Holomorphic Curves into PN(C)That Share a Set of Moving Hypersurfaces
Yang Liu
(School of Mathematics&Physics Science and Engineering,Anhui University of Technology,Maanshan,Anhui,243032)
Communicated by Ji You-qing
Abstract:Let F be a family of holomorphic curves of a domain D in C into a closed subset X in PN(C).Let Q1(z),···,Q2t+1(z)be moving hypersurfaces in PN(C)located in pointwise t-subgeneral position with respect to X.If each pair of curves f and g in F share the set{Q1(z),···,Q2t+1(z)},then F is normal on D.This result greatly extend some earlier theorems related to Montel’s criterion.
Key words:Holomorphic mapping,normal family,value distribution theory,complex projective space,hypersuface
1 Introduction and Statements
One of the most striking results in complex analysis is the Picard’s little theorem which can be stated as follows(see[1]–[2]).
Theorem A A meromorphic function in the complex plane C omits three distinct points in the extend complex plane is a constant.
Let D be a domain in C and F a family of meromorphic functions defined in D.F is said to be normal in D,in the sense of Montel,if each sequence in F contains a subsequence,which converges spherically locally uniformly in D to a meromorphic function or∞(see[1]–[3]).The normality corresponding to Theorem A can be stated as follows.
Theorem B[4]Let F be a family of meromorphic functions on a plane domain D which omit three distinct values a,b,c in the extend complex plane.Then F is normal on D.
Note the condition that each function f in F omits three values a,b,c means that the pre-image set f−1({a,b,c})= ∅,Fang and Hong[5]extended Theorem B and obtained
Theorem C[5]Let F be a family of meromorphic functions on a plane domain D,and let a,b,c be three distinct values in the extended complex plane.If each pair of functions f and g in F,f−1({a,b,c})=g−1({a,b,c}),then F is normal on D.
In order to state the results,we recall some facts firstly.
Definition 1.1 Let Q1,···,Qq(q ≥ t+1)be hypersurfaces in the complex projective space PN(C)and X⊆PN(C)be a closed set(with respect to the usual topology of a real manifold of dimension 2N).We say that the hypersurfaces are located in t-subgeneral position with respect to X,if for any 1 ≤ j0< ··· In the particular case X=PN(C),we have Definition 1.2 Let Q1,···,Qq(q ≥ t+1)be hypersurfaces in PN(C).We say that the hypersurfaces are located in t-subgeneral position if for any 1 ≤ j0< ··· If a set of hypersurfaces in PN(C)are located in N-subgeneral position,we also say that they are located in general position. Remark 1.1[6]Neither the dimension of X nor the dimension of the ambient projective space is important in the formulation of Definition 1.1.Only the intersection pattern in the assumption of Definition 1.1 is relevant. We do not assume t≥N in the assumption of Definition 1.1,but the assumption of Definition 1.1 can be satisfied only if t≥N. In 1972,Fujimoto[7]and Green[8]obtained the following Picard-type theorem for holomorphic mappings of several complex variables into PN(C)related to hyperplanes. Theorem D[7],[8]Suppose that f is a holomorphic mapping from Cminto PN(C).If f omits 2N+1 hyperplanes in PN(C)located in general position,then f is constant. In the case of hypersurfaces,Eremenko[6]obtained a Picard-type theorem for holomorphic curves into PN(C)as follows. Theorem E[6]Let X be a closed subset of PN(C)and let Q1,···,Q2t+1be hypersurfaces in PN(C)located in t-subgeneral position with respect to X.Then every holomorphic mapping f from C intois constant. Let Q be a fixed hypersurface of degree d in PN(C),which is defined by a homogeneous polynomial P(x0,···,xN)∈ C[x0,···,xN],i.e., Denote by HDthe ring of all holomorphic functions on D.A moving hypersuface(on D)Q(z)is of degree d in PN(C)generalize,to every z0∈D,a fixed hypersurface given by where the coefficients ai0···iN(z)are holomorphic functions on D without common zeros. Definition 1.3[9]Let Q1(z),···,Qq(z)(q ≥ t+1)be moving hypersurfaces in PN(C)and X⊆PN(C)be a closed set.We say that moving persurfaces are in pointwise t-subgeneral position with respect to X,if for each z ∈ D,the fixed hypersurfaces Q1(z),···,Qq(z)are in t-subgeneral position with respect to X. In[10],Tu and Cao proved a normal criterion for families of holomorphic mappings of several complex variables into PN(C)with moving hypersurfaces in pointwise general position related to the Eremenko’s Picard-type theorem. Theorem F[10]Let F be a family of holomorphic mappings of a domain D in Cminto PN(C),and Q1(z),···,Q2t+1(z)be moving hypersurfaces in PN(C)located in pointwise t-subgeneral position with respect to PN(C).If each f in F omits Qj(z)(j=1,···,2t+1),then F is a normal family on D. Remark 1.2 We have the following slightly stronger version of Theorem F: Let F be a family of holomorphic mappings of a domain D in Cminto X,a closed subset of PN(C),and Q1(z),···,Q2t+1(z)be moving hypersurfaces in PN(C)located in pointwise t-subgeneral position with respect to X.If each f in F omits Qj(z)(j=1,···,2t+1),then F is a normal family on D. In fact,in the proof of Theorem F,we see that the sequence of holomorphic mappings gk(ξ):=fk(pk+rkukξ)converges uniformly on compact subsets of C to a nonconstant holomorphic mapping g(ξ)of C into PN(C)(see[10],pp.173).Thus,the hypothesis the image of fkis contained in a subset X implies that image of gkand hence g(C)is contained in X. Recently,Yang et al.[11]proved the following normality criterion theorem. Theorem G[11]Let F be a family of holomorphic mappings of a domain D in C into PN(C)and H1,···,H2N+1be hyperplanes in PN(C)located in general position.If,for each any two mappings f,g∈F, then F is normal on D. In this paper,we study the case where the holomorphic mappings of a family can meet moving hypersurfaces and obtain the following result which improve and generalize Montel’s criterion,and Theorems C,F and G. Theorem 1.1 Let X ⊆ PN(C)be a closed subset and Q1(z),···,Q2t+1(z)be moving hypersurfaces in PN(C)located in pointwise t-subgeneral position with respect to X.Let F be a family of holomorphic mappings of a domain D in C into X.If any two mappings f,g∈F, then F is normal on D. For the case of fixed hypersurfaces,we immediately have the following corollary: Corollary 1.1 Let F be a family of holomorphic mappings of a domain D in C into PN(C)and let Q1,···,Q2N+1be hypersurfaces in PN(C)located in general position.If any two mappings f,g∈F, then F is normal on D. In[12],Fujimoto defined the notion of a meromorphically normal family of meromorphic mappings of several complex variables into PN(C).We note that a meromorphic mapping of one complex variable into PN(C)must be holomorphic,we have the following corollary:Corollary 1.2 Let X ⊆ PN(C)be a closed subset and Q1(z),···,Q2t+1(z)be moving hypersurfaces in PN(C)located in pointwise t-subgeneral position with respect to X.Let F be a family of meromorphic mappings of a domain D in C into X.If any two mappings f,g∈F, then F is meromorphically normal on D. We start with relevant notions and definitions.For details see[13]–[15].Recall that the N-dimensional complex projective space PN(C)=CN+1−{0}/ ∼,where(a0,···,aN)∼(b0,···,bN)if and only if(a0,···,aN)= λ(b0,···,bN)for some λ ∈ C.We denote by[a0: ···:aN]the equivalence class of(a0,···,aN). Let D be a domain in C,f:D→PN(C)be a holomorphic map,and U be an open set in D.Any holomorphic map f:U→CN+1such that P(f(z))≡f(z)in U is called a representation of f on U,where P:CN+1−{0}→PN(C)is the standard projective map. Definition 2.1 For an open subset U of D,we call a representation f=(f0,···,fN)a reduced representation of f on U if f0,···,fNare holomorphic functions on U without common zeros. Next,we let Q(z)be a moving hypersurface of degree d given by Then,for any reduced representation f of a holomorphic map f,we define the holomorphic function whose values depend on the representation f.Moreover,we can write f instead of f when the properties are independent of the choice of a reduced representation.For example,we can study the function,where H is a fixed hyperplane in PN(C). Remark 2.1 As is easily seen,if both fj:Uj→CN+1are reduced representations of f for j=1,2 with U1∩ U2≠ ∅,then there is a holomorphic function h(≠0):U1∩ U2→ C such that f2=hf1on U1∩U2. Next,we recall the definition of a normal family. Definition 2.2 A family F of holomorphic maps of a domain D in Cminto PN(C)is said to be normal on D if any sequence in F contains a subsequence which converges uniformly on compact subsets of D to a holomorphic map of D into PN(C)and F is said to be normal at a point a in D if F is normal on some neighborhood of a in D. Using the Fubini-Study metric form on PN(C),we see that a sequence{fn}∞n=1of holomorphic maps of D into PN(C)converges uniformly on compact subsets of D to a holomorphic map f if and only if for any a∈D each fNhas a reduced representation fn=(fn0,fn1,···,fnN)on some fixed neighborhood U of a in D such that{fni}∞n=1converges uniformly on compact subsets of U to a holomorphic function fi(i=0,1,···,N)on U with the property that f=(f0,f1,···,fN)is a reduced representation of f on U. Let S be a non-empty open subset of a domain D in Cmsuch that D−S is an analytic set in D.Let f be a holomorphic mapping of S into PN(C).Let U be a non-empty connected open subset of D.A holomorphic mapping f(≢ 0)from U into CN+1is said to be a representation of f on U if A holomorphic mapping f:S→PN(C)is said to be a meromorphic mapping from D into PN(C)if for each a ∈ D,there exists a representation f(z)=(f0(z),f1(z),···,fN(z))of f on some neighborhood of a in D.Moreover,we can choose representations of f so as to satisfy the condition A representation of f satisfying this condition is refered to as a reduced representation of f on U. For a meromorphic mapping f into PN(C)we denote by I(f)the set of all points of indetermination of f,which is given by the condition if f has a reduced representation f(z)=(f0(z),f1(z),···,fN(z))on an open subset U of D.Obviously,a meromorphic mapping f from D into PN(C)is holomorphic on D if and only if I(f)=∅. Definition 2.4 Let F be a family of meromorphic mappings of a domain D⊂Cminto PN(C).We call F to be meromorphically normal if any sequence in F has an meromorphically convergent subsequence and to be normal at a∈D if any sequence in F has a subsequence which converges compactly on some neighborhood of a(maybe depending on each sequence). We remark that a meromorphically normal family fail to be(holomorphically)normal even in case all mappings of the family are holomorphic.For example,the sequence is not normal on∆,the unit disk,though it is meromorphically normal on∆. To prove our result,we need the following lemma: Lemma 3.1[16]Let F be a family of holomorphic maps of a domain D in Cminto PN(C).The family F is not normal on D if and only if there exist sequences{fn}⊂F,{zn}⊂D with zn→ z0∈ D,{ϱn}with ϱn>0 and ϱn→ 0 and{un} ⊂ CmEuclidean unit vectors,such that hn(ξ):=fn(zn+ϱnunξ)converges uniformly on compact subsets of C to a nonconstant holomorphic mapping h of C into PN(C). The proofs of our results make full use of this lemma(not only sufficiency but also necessity).We now prove our main result. Proof of Theorem 1.1 Fix z0∈D and f0∈F,we separate two cases. It follows from the hypothesis that for each f∈F, Hence,for each f∈F,we get Thus F is normal on U by Theorem F and Remark 1.2. Subcase 2.1.For each j=1,2,···,2t+1,f0(D) ⊆ Qj(z). Because the zeros of⟨f0,Qj(z)⟩,j ∈ {1,2,···,2t+1}have no accumlation point,there exists a neighbourhood U of z0such that where Hence,for each f∈F, Thus F is normal on U∗again by Theorem F and Remark 1.2. Since that Q1(z),···,Q2t+1(z)locate in pointwise t-subgeneral position with respect to X,for each fn,we have that fn(z0)is in at most t hypersurfaces in{Q1(z),···,Q2t+1(z)}.Therefore,we can find a subsequence(again denoted bysatisfying that,without loss of generality,.And hence,we have for any fn.Without loss of generality,we can suppose that Suppose that the degree of hypersurface Q1(z)is d.Let be the coordinate hyperplanes in PN(C).We now define holomorphic curves gnof U into PN+1(C)induced by the mapping i.e., The above definition is independent of the choice of the reduced representation of fn. For any z∈U,one can always find neighborhood V of z such that For our purpose,it suffices to show that(i=0,1,···,N)convergesuniformly on V. By theassumptions, the sequence ofholomorphicfunctionsconverges uniformly to.Notice that the functionsare holomorphic on V.Therefore,by Maximum Modulus Principle,for 0 ≤ i ≤ N,we get thatare uniformly bounded on V.It follows from Theorem B that there is a subsequence ofwhich is converges uniformly to a holomorphic function on V.And thus,is normal on U as claimed. We now return to the proof of the theorem. where ξ∈ C satisfies zn+ ϱnξ∈ U,converges uniformly on compact subsets of C to a nonconstant holomorphic mapping F of C into PN(C). Correspondingly,we obtain converges uniformly on compact subsets of C to a holomorphic mapping G of C into PN+1(C),where gn(n=1,2,···)are holomorphic mappings of u into PN+1(C)defined as above.If we take a reduced representation of F on C,then we can obtain a reduced representation of G on C as follow: In addition,we deduce that G is nonconstant.Else,G is a constant mapping. If 〈F,Q1(z0)〉(ξ) ≡ 0,then the mappingis constant,so is F.If,then the mappingis constant outside a set of isolated points F−1(Q1(z0)).It follows from the uniqueness theorem that the mappingis constant on C,we also have that F is constant which leads to a contradiction.Again,by Lemma 3.1,is not normal on U.This is a contradiction with Claim.Hence,is a normal family on U. Subcase 2.2.There exists a j ∈ {1,2,···,2t+1}such that f0(D)⊆ Qj(z). Denote by J ⊂ {1,···,2t+1}such that i∈ J if and only if f0(D) ⊆ Qi(z).Then k:= ♯J ≤t.Set Then F is a family of holomorphic mappings of D into Xj,and{Qi(z)}i∉Jlocate in pointwise(t−k)-subgeneral position with respect to Xj.Without loss of generality,by taking subsequence we can assume that for any f ∈ F0(a subset of F)and i∉ J,we see that f0(D)⊆ Qi(z).Noting that using the conclusion which is obtained in Case 2.1,we can obtain F0is normal on some neighbourhood of z0.And hence,F is normal on D. We have completed the proof.






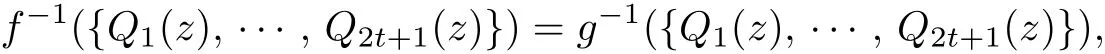
2 Auxiliary Results






3 Proofs










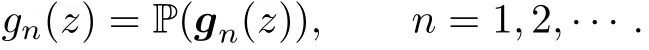







 Communications in Mathematical Research2019年2期
Communications in Mathematical Research2019年2期
