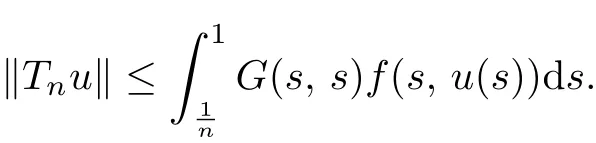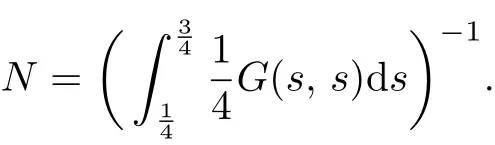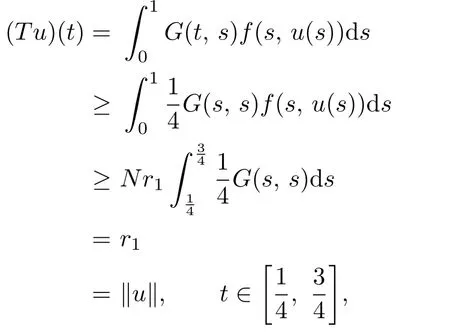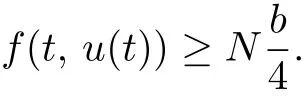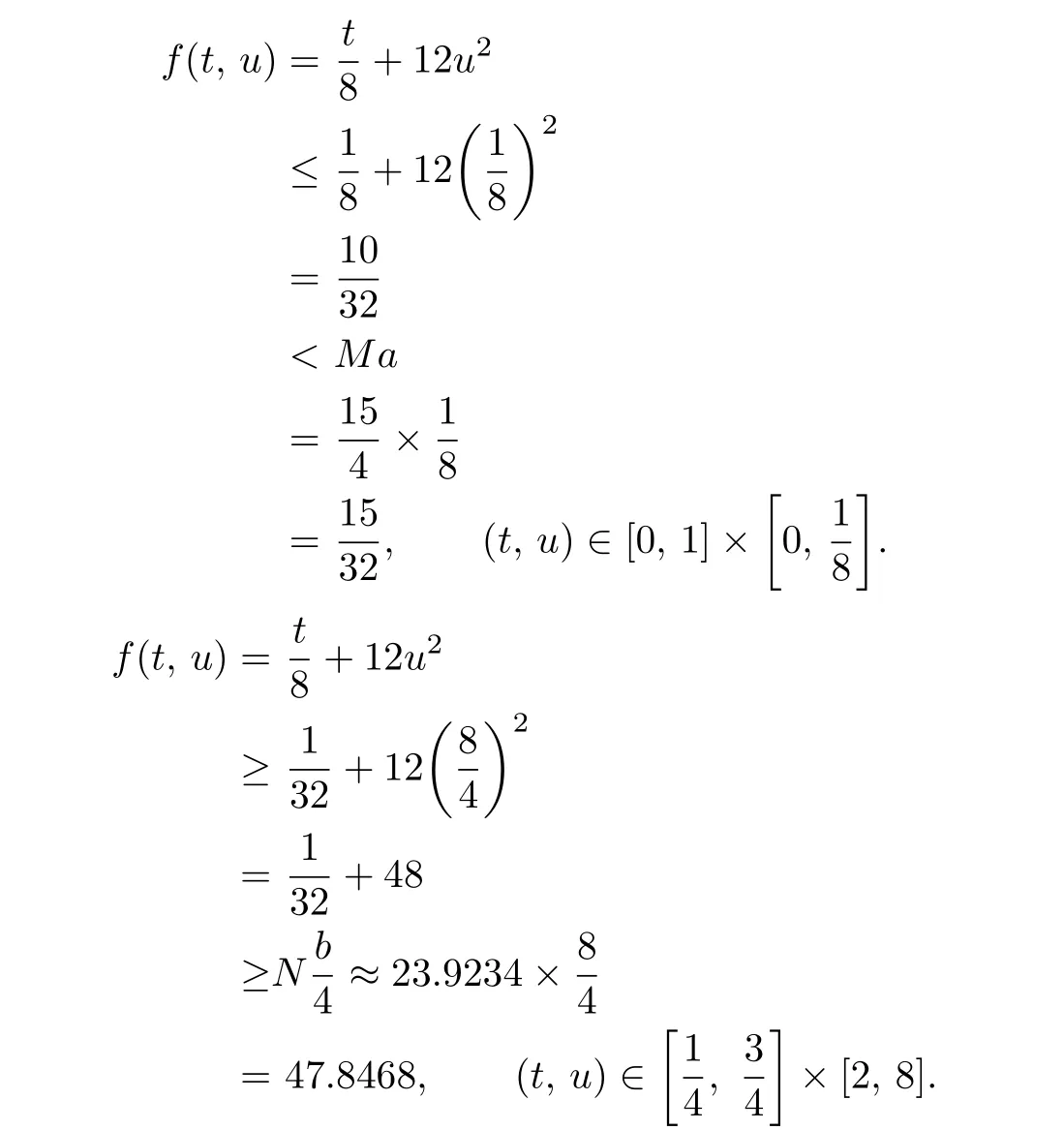Existence of Solutions for Fractional Differential Equations with Conformable Fractional Differential Derivatives
Wu Yue-xiang,Huo Yan-meiand Liang Hua-dong
(1.Department of Applied Mathematics,Shanxi University of Finance and Economics,Taiyuan,030006)
(2.College of Economics,Shanxi University of Finance and Economics,Taiyuan,030006)
Communicated by Ji You-qing
Abstract:A class of nonlinear fractional differential equations with conformable fractional differential derivatives is studied.Firstly,Green’s function and its properties are given.Secondly,some new existence and multiplicity conditions of positive solutions are obtained by the use of Leggett-Williams fixed-point theorems on cone.
Key words:conformable fractional derivative,singular Green’s function,fractional differential equation
1 Introduction
In this paper,we are concerned with the existence of three positive solutions to the following nonlinear conformable fractional differential equation boundary value problem(BVP)

where 1<α≤2 is a real number,Dαis the conformable fractional derivative,and f:[0,1]×[0,+∞)→[0,+∞)is a continuous function.One of the difficulties here is the corresponding Green’s function G(t,s)is singular at s=0.Based on the Leggett-Williams fixed point theorem on cone,we obtain sufficient conditions for the existence of three positive solutions to the conformable fractional boundary value problem(1.1)-(1.2).
Recently,the existence of positive solutions to the fractional differential equations has been of great interest,this is caused both by the intensive development of the theory of fractional calculus itself and by the varied applications in many fields of science and engineering,see,for instance,[1]–[3]and the references therein.
Bai and L¨u[4]considered the positive solutions for boundary value problem of nonlinear fractional differential equation with Riemann-Liouville fractional derivative,i.e.,

by defining Green’s function and using Krasnoselskiifixed point theorem,the existence and multiplicity of positive solutions of(1.3)-(1.4)are acquired.Kang et al.[5]studied the existence of three positive solutions to the following boundary value problem of nonlinear fractional differential equation

where λ>0 is a positive parameter andis the standard Riemann-Liouville fractional derivative,h:(0,1)→ (0,∞)is continuous with,and f:[0,∞)→ [0,∞)is continuous.Based on the Leggett-Williams fixed point theorem,some results for the existence of three positive solutions to the fractional boundary value problem(1.5)-(1.6)are obtained.
Afterwards,these methods attract many authors,and apply in all kinds of fractional differential equation boundary value problems,such as Riemann-Liouville fractional derivative problems(see[6]),Caputo fractional derivative problem(see[7]),impulsive problems(see[8]),integral boundary value problems(see[9]),etc.
In recent years,a new conformable fractional derivative was defined(see[10]–[12]),Dong and Bai[13]established the existence of positive solutions for nonlinear eigenvalue problems and some boundary value problems with conformable fractional differential derivatives.This motivated our study interesting with problem(1.1)-(1.2)by this new derivatives.
Duo to the corresponding Green’s function G(t,s)is singular at s=0,to the knowledge of the author,there are very few works on the existence and multiplicity of positive solutions of boundary value problems for above nonlinear fractional differential equation.
To ensure that readers can easily understand the results,the rest of the paper is planned as follows.In Section 2,we recall certain basic definitions and present some lemmas.In Section 3,by the use of approach method and Krasnoselkii’s fixed points theorem on cone we obtain that the existence conditions of BVP(1.1)-(1.2)has at least one positive solution or three positive solutions.In Section 4,we give an example as an application of our results.
2 Preliminaries
Definition 2.1[10]Let f:[0,+∞)→ R be a continuous function,its conformable fractional derivative of order α∈(n,n+1]is defined as

Then f is called differential of order α.
Remark 2.1 Let α ∈ (n,n+1].Then Dαtk=0,where k=0,1,2,···,n.
Lemma 2.1[10]Let f:[0,+∞)→R be a continuous function,α∈(n,n+1].Then

Definition 2.2[11]Let f:[0,+∞)→R be a continuous function,its fractional integer of order α∈(n,n+1]defined as
where In+1is n+1 integer operator.
Lemma 2.2[12]Let f be differential of order α,α ∈ (n,n+1].Then

if and only if

where ak∈ R,k=0,1,2,···,n.
Lemma 2.3[13]Let y∈C[0,1],α∈(1,2].Then the BVP

has unique solution

where

is called the Green’s function of the problem(2.3)-(2.4).
Lemma 2.4[13]Green’s function G(t,s)satisfies the following properties:

Lemma 2.5[14]Let E be a Banach space,Tn:E → E(n=3,4,···)be completely continuous,T:E →E.If for any bounded subset Ω of E,∥Tnu−Tu∥⇒ 0 as n→∞,then T:E→E is completely continuous.
Definition 2.3[14]Let P be a cone of a Banach space E.Then a continuous mapping θ:P → [0,+∞)is called concave functional if θ(tx+(1 − t)y)≥ tθ(x)+(1 − t)θ(y)for all x,y∈P,0 Lemma 2.6[15]Let E be a Banach space and P be a cone of E,c>0 be a constant,Pc={x ∈ P|∥x∥ ≤ c}.Suppose that there exists a concave nonnegative continuous functional θ on P with θ(u) ≤ ∥u∥ for u ∈.Let P(θ,b,d)={x ∈ P|b ≤ θ(x), ∥x∥ ≤ d}.Let A:be completely continuous operator,and there exists a constant 0 (H1) The set{x ∈ P(θ,b,d)| θ(x)>b}is nonempty and θ(Ax)>b for all x ∈P(θ,b,d); Communications in Mathematical Research2019年2期
Communications in Mathematical Research2019年2期