Consequence Operators and Information Algebras

Xu Ge-ni and Luo Qing-jun

(College of Statistics,Xi’an University of Finance and Economics,Xi’an,710062)

Communicated by Du Xian-kun

Abstract:In this paper,the continuity of consequence operators is introduced.Relations between consequence operators and their associated information algebras are mainly explored.It is shown that,for any given consequence operator,the associated information algebra can be directly constructed without any additional conditions.Furthermore,if the consequence operators are continous or compact,then the associated information algebras are continuous or compact.

Key words:information algebra,consequence operator,continuity,compactness

1 Introduction

Information is considered as collections of distinct,abstract items or elements—pieces or bodies of information.Combination of pieces of information and focusing of information are two fundamental operations on information.The two operations must be subdued to a set of intuitive axioms.In this way an information algebra is formed which can be seen as generic algebraic structures for local computation and inference(see[1]).Some related studies show that the framework of information algebra covers a wide range of different instances from constraint systems,propositional logic to belief functions,relational algebra and others(see[1]–[3]).

Information algebra is a generic structure closely related with information processing.However,real computer can treat only “ finite” information.This means that not every information can be exactly represented and processed on real computers.However“in finite” information may possibly be approximated by “ finite” information and thus processed at least approximately.To model this situation some compactness conditions have to be introduced into the algebra,leading to compact information algebras(see[1],[3]and[4]).Continuous information algebra is the generalization of compact information algebra(see[5]and[6]).

In order to give a different way to represent information and information algebra,the concept of consequence operator is introduce.Consequence operator(see[2])is described by a language and an entailment relation on sets of formulae.References[2]and[4]show that any given information algebra can induce corresponding consequence operator and in turn,the associated information algebra is obtained on the consequence operator provided that the consequence operator satisfies the properties of interpolation and deduction.This means that compact consequence operator induced corresponding compact information algebra,provided that consequence operator is compact and satisfies the theorem of interpolation and deduction.Complexity of interpolation and deduction makes the link between information algebra and consequence operator not clear.And so far the description of equivalent of interpolation and the deduction is not able to give.

Therefore,it is necessary to find a new way to induce the corresponding information algebra by consequence operator,and also the new method should ensure the corresponding relationship between compact information algebra and compact consequence operator is clear.To address the issue,in this paper we firstly decompose the operation of focusing by consequence operator.Based on it,a complete and direct characterization of the relationship between information algebra and consequence operator is given.Secondly,the continuous consequence operator is defined and the relationship between continuous information algebra and continuous consequence operator is given.At last,according to the above conclusions,the paper shows that the compactness can be preserved from consequence operator to its associated information algebra.

The main work and the organization of this paper are as follows.In Section 2,some basic notions and examples of consequence operator and information algebra are introduced.Furthermore,the concepts of continuous(compact)consequence operator and continuous(compact)information algebra are given.Section 3 shows that,for any given consequence operator,the associated information algebra can be constructed directly without any additional conditions.Section 4 demonstrates the correspondence from continuous(or compact)consequence operators to continuous(or compact)information algebras.

2 Preliminaries

In this part,some basic notations on information algebra and consequence operator that we use in the following discussion will be introduced.

Definition 2.1[1]A tuple(Φ,D)is a system with two operations ·and π,where Φ is a set of elements and D is a lattice:

(1)Combination:Φ ×Φ → Φ,(φ,ψ)→ φ·ψ;

(2)Focusing:Φ ×D → Φ,(φ,x)→ πx(φ).

We impose the following axioms on(Φ,D)and call it an information algebra:

(1)Semigroup:Φ is associative and commutative under combination,and there is an element e such that for all φ ∈ Φ with e·φ = φ·e;

(2)Transitivity:For φ ∈ Φ and x,y ∈ D,πy(πx(φ))= πx∧y(φ);

(3)Combination:For φ,ψ ∈ Φ,x ∈ D,πx(πx(φ)·ψ))= πx(φ)·πx(ψ);

(4)Support:For φ ∈ Φ,there is an x ∈ D such that πx(φ)= φ;

(5)Idempotency:For φ ∈ Φ and x ∈ D,φ·πx(φ)= φ.

Suppose that(Φ,D)is an information algebra.We write φ ≤ ψ means that an information ψ is more informative than another information φ,i.e.,φ ·ψ = ψ.The order relation≤is a partial order on information algebra.In fact,φ≤φ follows from idempotency φ·φ= φ.Then φ ≤Φ and Φ ≤ φ imply φ=Φ because φ=φ·Φ =Φ.Lastly,φ≤Φ and Φ ≤ η imply φ ≤ η.This follows since φ·Φ = Φ and Φ·η = η that φ·η=(φ·Φ)·η = Φ·η = η.

Example 2.1 Let U be an initial universe set and P(U)denote the power set of U.Let E be a set of parameters which usually are initial attributes,characteristics,or properties of objects in U.A pair(F,A)is called a soft set over U(see[7]),where A⊆E and F is a mapping given by F:A 7→P(U).Especially,F:A 7→U is represented as(U,A).

Let(F,E)={F:E 7→P(U)},there are two operations defined on(F,E)as follows:

(1)(F,E)·(G,E)=(H,E),e∈ E,H(e)=F(e)∩G(e);

(2)for any C ⊆ E,πC(F,E)=(G,E),

According to the definition,we are going to show that(F,E)is an information algebra with two operations ·and π as above.

Semigroup:F is associative and commutative under·,(U,E)is a neutral element such that

Transitivity:For any B,C⊆E,

where

Hence,

Combination:On the one hand,

where

Hence,

On the other hand,

where

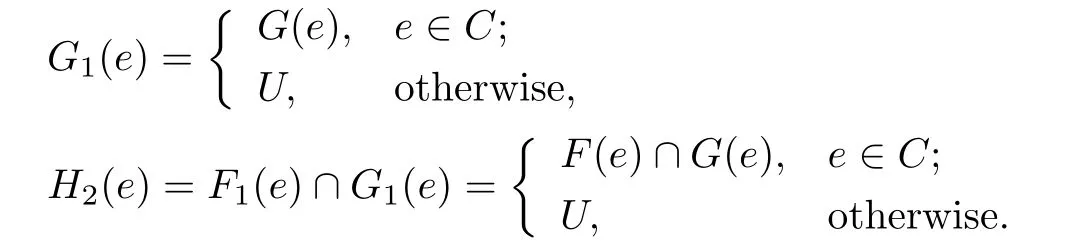
Thus,for any e∈E,one has

That is to say

Support:

Idempotency:

The proof above shows that(F,E)is an information algebra.

In general,only “ finite” information can be treated in computer.Then,compact information algebra that each information can be approximated by some “ finite” and coarse information is proposed by Kohlas(see[1]and[4]).Here a generalized notion called continuous information algebra is also given.

Definition 2.2 A system(Φ,Φf,D)where(Φ,D)is an information algebra,the lattice D has a top element,Φf⊆ Φ is closed under combination and contains the empty information e,satisfying the following axioms of convergence and density,is called a continuous information algebra(see[5]and[6]),and the elements of Φfare called finite.

(1)Convergency:If X ⊆Φfis a directed set,then the supremum ∨X exists.

(2)Density:For all φ ∈ Φ,

If a continuous information algebra satisfies the following strong density and compactness,then it is called a compact information algebra(see[1]).

(3)Strong density:For all φ∈ Φ,x∈ D,

(4)Compactness:If X ⊆ Φfis a directed set,and φ ∈ Φfsuch that φ ≤ ∨X,then there exists a ψ ∈ X such that φ ≤ ψ.

Data and facts are described in formal systems like computers in a formal language.Here we consider a language as a set L of well formed sentences.Data,facts and information are then expressed by subsets X of sentences of L,certain sentences can be deduced from others.In order to express the information contained in a set of sentences we need therefore an entailment relation defined between sets of sentences X⊆L and A∈L.The notation X⊢A say that the sentences A can be derived from the sentences X,that X entails A.This relation must satisfy the following conditions:

(E1)X⊢A for each A∈X;

(E2)If X⊢B for each B∈Y and Y⊢A,then X⊢A.

Lemma 2.1[4]If X⊆Y and X⊢A,then Y⊢A.

Lemma 2.2[4]For X⊆L,define C(X)={A∈L|X⊢A}.Then

(C1)X⊆C(X)for every subset X⊆L;

(C2)C(C(X))=C(X)for every subset X⊆L;

(C3)If X⊆Y,then C(X)⊆C(Y).

An operator satisfying conditions(C1)–(C3)is called a consequence operator.

Example 2.2 If X⊢a⇔a≤∨X for X⊆[0,1],then C(X)={a∈[0,1]:a≤∨X}is a consequence operator on[0,1].

In the following we give its proof.

It is obvious that X⊢a is an entailment relation.

(1)If a∈X,then a∈C(X).Hence X⊆C(X).So(C1)holds.

(2)We have C(C(X))={a∈[0,1]:a≤∨C(X)}.If a∈C(C(X)),then C(X)⊢a.But,for every element c∈C(X),c≤∨X and X⊢c.(E2)implies X⊢a and a∈C(X).This shows that C(C(X))⊆C(X).The converse inclusion holds by(C1).Hence we obtain that C(C(X))=C(X)and(C2)holds.

(3)Assume X ⊆Y.If a∈C(X),then a≤∨X.X ⊆Y means that∨X ≤∨Y.This shows that a≤∨Y and(C3)holds.

Let{Xi⊆L:i∈I}be a directed subset family of L,where I is a countable set.If a consequence operator C satisfies

then it is called continuous.

Let X⊆L be a directed set.If a consequence operator C satisfies

(C5)C(X)=∪{C(Y):Y⊆X,Y is finite},

then it is called compact(see[4]).

In the following we give its proof.

Thus we indicate that the consequence operator C(X)is continuous.

The following conclusion shows that the compact consequence operator is continuous.

Proposition 2.1 If a consequence operator C is compact,then the consequence operator C is continuous.

Proof. Let X ⊆ ΦC={C(X):X ⊆L}be a direct set.is so obvious byNow we have to show that

If Y⊆X and Y is finite,then there exists a Z∈X such that Y⊆Z because of the directionality of X,and so C(Y)⊆C(Z).Therefore,

The proof above shows that C is continuous.

3 Information Aalgebra Induced by Consequence Operator

In[4],it is shown that consequence operator induce corresponding information algebra,provided that the consequence operator is compact and satisfies the interpolation and the deduction theorem.This is one link between the two notions of information algebra and consequence operator.The following conclusion indicates that consequence operator can induce directly corresponding information algebra without any other additional conditions.

Theorem 3.1 Let C be a consequence operator and ΦC={C(X):X ⊆ L}.We define operations of combinations and focusing as follows:for C(X),C(Y)∈ΦC,L∈S,where S is a lattice,L∈S and S⊆P(L),P(L)is the power set of L,

Then(ΦC,S)is an information algebra with the operations ·and π.

Proof. The axiom of semigroup is correct obviously and C(∅)is the unite element.Now we check the other axioms.

Transitivity:For L,M∈S,

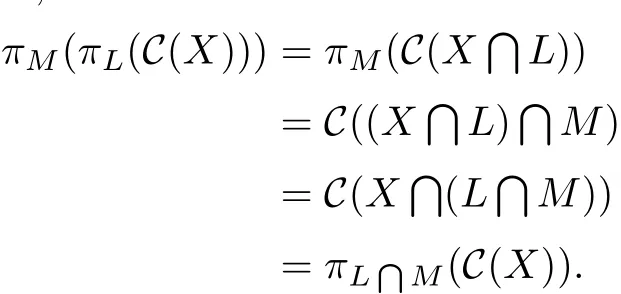
Combination:For X,Y⊆L,L∈S,

Support:For L∈S,

Idempotency:For X⊆L,L∈S,

The proof above implies that(ΦC,S)is an information algebra.

In fact,from the new definition above,we can obtain that not only a consequence operator induces directly an information algebra,but also the continuity and compactness are remained.

4 Continuity and Compactness Between Consequence Operator and Information Algebra

Theorem 4.1 If C is a continuous consequence operator,then(ΦC,ΦC,f,S)is a continuous information algebra,where ΦC,f={C(X):X ⊆ L,X is finite}.

Proof. Convergency:Assume that Γ ⊆ ΦC,fis directed.Thenis obviously correct.We have to show that,i.e.,we must show that.Therefore assume that,thenbecause of the continuity of consequence operator C.There exits a finite set such that A∈C(X).Note now that each element of Xis in at least one of the closed set of Γ .Therefore,since Γ is directed,there exists a closed set Z∈Γ such that X⊆Z.So we obtain

Density:It is obvious that there is

If A∈C(X),then C(A)⊆C(X).By the continuity of C,we have

where Y∈L is finite.Therefore,

So we have

Corollary 4.1 If C is a compact consequence operator,then(ΦC,ΦC,f,S)is a continuous information algebra.

In fact,if C is a compact consequence operator,then(ΦC,ΦC,f,S)is not only a continuous information algebra,but also a compact information algebra.

Theorem 4.2 If C is a compact consequence operator,then(ΦC,ΦC,f,S)is a compact information algebra.

Proof. By Proposition 2.1,we only need to prove the case of strong density and compactness.

Strong density:By the compactness of C we have

where C(X)∈ΦC,L∈S.

By Y⊆X∩L we have

Thus,

Then

By C(Y)⊆C(X)we have

Therefore,

Compactness:Let X ⊆ΦC,fbe a direct set,C(Y)∈ΦC,f,and.Then each element of C(Y)is in at least one of the closed sets of X.Since X is directed,there exists an element Z∈X such that C(Y)⊆Z=C(Z).

5 Conclusions

We define the concept of continuous consequence operator and study the relationships between consequence operator and its information algebra.We obtain that the consequence operator can induce corresponding information algebra without any other additional conditions.Theorems 3.1 and 4.1 show that there exists correspondence between consequence operator and information algebra on continuity and compactness.Consequence operator is another representation of information algebra,which places the algebra into the realm of logic.Based on this relation,computation,not only in information algebra,but also in continuous information algebra or compact information algebra,can be transformed into deduction in logic,which provides a theoretical basis for the following studies between information algebra and logic.