Hypersemilattice Strongly Regular Relations on Ordered Semihypergroups
Tang Jianand Xie Xiang-Yun
(1.School of Mathematics and Statistics,Fuyang Normal University,Fuyang,Anhui,236037)
(2.School of Mathematics and Computational Science,Wuyi University,Jiangmen,Guangdong,529020)
Communicated by Du Xian-kun
Abstract:In this paper,we first consider the regular and strongly regular relations on ordered semihypergroups in detail.In particular,we introduce the concepts of the hypersemilattice strongly regular relations and complete hypersemilattice strongly regular relations on ordered semihypergroups,and investigate their related properties.Furthermore,the properties of hyper filters of an ordered semihypergroup are studied,and several related applications are given.Especially,we prove that the equivalence relation N on an ordered semihypergroup S is the least complete hypersemilattice strongly regular relation on S.
Key words:ordered semihypergroup,strongly regular relation,hyper filter
1 Introduction
As we know,an ordered semigroup(S,·,≤)is a semigroup(S,·)with an order relation“≤”such that a≤b implies xa≤xb and ax≤bx for any x∈S.Ordered semigroups have several applications in the theory of sequential machines,formal languages,computer arithmetics and error-correcting codes.Similar to the theory of congruences on semigroups,congruences on ordered semigroups play an important role in studying the structures of ordered semigroups.For any congruence ρ on an ordered semigroup S,in general,we do not know whether the quotient semigroup S/ρ is also an ordered semigroup.Even if S/ρ is an ordered semigroup,the order on S/ρ is not necessarily relative to the order on the original ordered semigroup S.As to the above-mentioned questions,Kehayopulu and Tsingelis[1]–[2]introduced the concept of pseudoorder on an ordered semigroup S and proved that if σ is a pseudoorder on S,then there exists a congruence¯σ on S such that S/¯σ is an ordered semigroup.Since then,Xie and Wu[3]introduced the concept of regular semilattice congruences on an ordered semigroup S,and proved that the semilattice congruences N on S is the least regular semilattice congruence but not the least semilattice congruence on S.
The hyperstructure theory was introduced in 1934 by Marty[4]at the 8th congress of Scandinavian Mathematicians.Nowadays,hyperstructures have a lot of applications in several domains of mathematics and computer science,for example,see[5]and[6].In the hyperstructure theory,semihypergroups are the simplest algebraic hyperstructures which are a generalization of concept of semigroups.Recently,a theory of hyperstructures on ordered semigroups has been developed.In[7],Heidari and Davvaz applied the theory of hyperstructures to the ordered semigroups and introduced the concept of the ordered semihypergroups,which is a generalization of the concept of the ordered semigroups.Later on,a lot of papers on ordered semihypergroups have been written,for instance,see[8]–[12].It is worth pointing out that Davvaz et al.[8]introduced the concepts of the regular and strongly regular relations on ordered semihypergroups,and extended some results in[1]on ordered semigroups to ordered semihypergroups.As a further study of(strongly)regular relations on ordered semihypergroups,in this paper we define and study the hypersemilattice strongly regular relations and complete hypersemilattice strongly regular relations on ordered semihypergroups,and extend some results in ordered semigroups to ordered semihypergroups.Furthermore,we study the properties of hyper filters of an ordered semihypergroup in detail,and give several applications of hyper filters in ordered semihypergroups.Especially,we consider the equivalence relation“N”on an ordered semihypergroup,which is defined by aNb if and only if N(a)=N(b),where N(x)is the hyper filter of S generated by x(x∈S).We prove that N is the least complete hypersemilattice strongly regular relation on S.As an application of the results of this paper,the corresponding results of semihypergroups(without order)and ordered semigroups are also obtained by moderate modifications.
2 Preliminaries and Some Notations
Recall that a hypergroupoid(S,◦)is a nonempty set S together with a hyperoperation,that is a map◦:S×S→P∗(S),where P∗(S)denotes the set of all the nonempty subsets of S.The image of the pair(x,y)is denoted by x◦y.If x∈S and A,B are nonempty subsets of S,then A◦B is defined by A◦a◦b.Also A◦x is used for A◦{x}and x◦A for{x}◦A.Generally,the singleton{x}is identified by its element x.
We say that a hypergroupoid(S,◦)is a semihypergroup if the hyperoperation “‘◦” is associative,that is,

for all x,y,z∈S(see[5]).
As we know,an ordered semigroup(S,·,≤)is a semigroup(S,·)with an order relation“≤”such that a≤b implies xa≤xb and ax≤bx for any x∈S.In the following,we extend the concept of the ordered semigroups to the hyper version,and introduce the concept of the ordered semihypergroups from[7].
Definition 2.1 An algebraic hyperstructure(S,◦,≤)is called an ordered semihypergroup(also called po-semihypergroup in[7])if(S,◦)is a semihypergroup and(S,≤)is a partially ordered set such that for any x,y,a∈S,x≤y implies a◦x≼a◦y and x◦a≼y◦a.Here,if A,B∈P∗(S),then we say that A≼B if for every a∈A there exists a b∈B such that a≤b.
Clearly,every ordered semigroup can be regarded as an ordered semihypergroup(see[10]).Throughout this paper,unless otherwise mentioned,S denotes an ordered semihypergroup.
For∅≠H⊆S,we define

For H={a},we write(a]and[a)instead of({a}]and[{a}),respectively.
By a subsemihypergroup of an ordered semihypergroup S we mean a nonempty subset A of S such that A◦A⊆A.A nonempty subset A of an ordered semihypergroup S is called a left(resp.right)hyperideal of S if
(1)S◦A⊆A(resp.A◦S⊆A),and
(2)if a∈A,b≤a with b∈S,then b∈A.
If A is both a left and a right hyperideal of S,then it is called a(two-sided)hyperideal of S(see[7]).We denote by L(a)(resp.R(a),I(a))the left(resp.right,two-sided)hyperideal of S generated by a(a∈S).One can easily prove that

A hyperideal I of an ordered semihypergroup S is called completely prime if for any two elements a,b of S such that(a◦b)∩T ≠ ∅,we have a ∈ T or b∈ T(see[10]).I is called prime if for any element a,b of S such that a◦b⊆T,we have a∈T or b∈T.I is called completely semiprime if for any element a of S such that(a◦a)∩T ≠ ∅,we have a∈ T.
Lemma 2.1 Let S be an ordered semihypergroup.Then the following statements hold:
(1)A ⊆ (A],∀A ∈ P∗(S);
(2)If A⊆B⊆S,then(A]⊆(B];
(3)(A]◦(B]⊆ (A◦B]and((A]◦(B]]=(A◦B],∀A,B ∈ P∗(S);
(4)((A]]=(A],∀A ⊆ S;
(5)For any left(resp.right,two-sided)hyperideal T of S,we have(T]=T;
(6)For any a∈S,(S◦a],(a◦S]and(S◦a◦S]are a left hyperideal,a right hyperideal and a hyperideal of S,respectively.Proof.Straightforward.
Lemma 2.2 Let S be an ordered semihypergroup and{Ai|i∈I}a family of left(resp.right,two-sided)hyperideals of S.Thenis a left(resp.right,two-sided)hyperideal of S andis also a left(resp.right,two-sided)hyperideal of S if
Proof. Straightforward.
The reader is referred to[6],[13]and[14]for notation and terminology not defined in this paper.
3 Hypersemilattice Strongly Regular Relations on Ordered Semihypergroups
In this section,we first consider the regular and strongly regular relations on ordered semihypergroups.Furthermore,we introduce the concepts of the hypersemilattice strongly regular relations and complete hypersemilattice strongly regular relations on ordered semihypergroups,and investigate some their related properties.
Let ρ be an equivalence relation on a semihypergroup(S,◦).If A and B are nonempty subsets of S,then we writeto denote that for every a∈ A,there exists a b∈ B such that aρb and for every b ∈ B,there exists an a ∈ A such that aρb.We writeif for every a∈ A and b∈ B we have aρb.
It is well known that the regular and strongly regular relations have an important role in the theory of algebraic hyperstructures.In the following let us recall the concepts of the regular and strongly regular relations on semihypergroups from[5].
Definition 3.1 An equivalence relation ρ on a semihypergroup(S,◦)is called left(resp.right)regular relation if for every(x,y)∈ S×S,the implication xρy⇒(a◦x)(a◦y)(resp.xρy⇒ (x◦a)(y◦a)),for all a∈S,is valid.ρ is called a regular relation if it is a both left and right regular relation.
Definition 3.2 An equivalence relation ρ on a semihypergroup(S,◦)is called strongly left(resp.strongly right)regular relation if for every(x,y)∈S×S,the implication xρy⇒(a◦x)(a◦y)(resp.xρy⇒ (x◦a)(y◦a)),for all a∈S,is valid.ρ is called a strongly regular relation if it is a both strongly left and strongly right regular relation.
Remark 3.1 (1)Every strongly regular relation is a regular relation on a semihypergroup.
(2)By Definitions 3.1 and 3.2,we can see that the regular(strongly regular)relations on ordered semihypergroups can be defined exactly as in the case of semihypergroups.Thus it is unnecessary to repeat the concepts of the regular and strongly regular relations on ordered semihypergroups.For the details,we can also see[8].
Let(S,◦)be a semihypergroup and ρ an equivalence relation on S.Let(a)ρbe the equivalence class of a with respect to ρ and let S/ρ ={(a)ρ|a ∈ S}.The hyperoperation“⊗” on S/ρ is defined as follows:

Lemma 3.1[5]Let(S,◦)be a semihypergroup and ρ an equivalence relation on S.Then ρ is a regular relation(resp.strongly regular relation)if and only if(S/ρ,⊗)is a semihypergroup(resp.semigroup).
Definition 3.3 A regular(strongly regular)relation ρ on an ordered semihypergroup(S,◦,≤)is called hypersemilattice regular(strongly regular)relation ifand(a◦b)(b◦a)for any a,b∈ S.
Remark 3.2 In particular,if(S,◦,≤)is an ordered semigroup,then a hypersemilattice regular(strongly regular)relation on S is exactly a semilattice congruence defined in[15].
Lemma 3.2 Let ρ be a hypersemilattice regular relation on an ordered semihypergroup(S,◦,≤).Then,we have
(1)(a)ρ⊗ (a)ρ=(a)ρ, ∀a ∈ S.
(2)(a)ρ⊗(b)ρ=(b)ρ⊗(a)ρ, ∀a,b ∈ S.
Proof. (1)Assume that ρ is a hypersemilattice regular relation on an ordered semihypergroup(S,◦,≤).Let a∈ S.Then,and we have xρa for any x ∈ a◦a.Thus we have

(2)Suppose that ρ is a hypersemilattice regular relation on an ordered semihypergroup(S,◦,≤)and a,b∈ S.Then


which implies that

Similarly,we can also prove the inverse inclusion.Therefore,

Lemma 3.3 Let ρ be a hypersemilattice strongly regular relation on an ordered semihypergroup(S,◦,≤).Then
(1)(a)ρ⊗ (a)ρ=(a)ρ, ∀a ∈ S;
(2)(a)ρ⊗(b)ρ=(b)ρ⊗(a)ρ, ∀a,b ∈ S.
Proof.The proof is straightforward by Remark 3.1(1)and Lemma 3.2.
As we know,for a strongly regular relation ρ on an ordered semihypergroup S,the corresponding quotient structure S/ρ is not necessarily an ordered semigroup(see[8]).The following theorem provide a condition that S/ρ forms an ordered semigroup.
Theorem 3.1 Let(S, ◦, ≤)be an ordered semihypergroup and ρ a hypersemilattice strongly regular relation on S.Then(S/ρ,⊗,≤ρ)is an ordered semigroup with respect to the following hyperoperation:

and the partially ordered relation “≤ρ” on S/ρ defined as follows:

Proof.By Lemma 3.1,(S/ρ,⊗)is a semigroup.Moreover,the binary relation ≤ρis a partially ordered relation on S/ρ.Indeed,let(a)ρ∈ S/ρ.Since ρ is a hypersemilattice strongly regular relation on S,by Lemma 3.3(1),we have(a)ρ⊗(a)ρ=(a)ρand(a)ρ≤ρ(a)ρ.Thus the binary relation ≤ρis re flexive.Let(a)ρ≤ρ(b)ρ,(b)ρ≤ρ(a)ρ.Then we have(a)ρ⊗ (b)ρ=(a)ρand(b)ρ⊗ (a)ρ=(b)ρ.By hypothesis and Lemma 3.3(2),(a)ρ⊗ (b)ρ=(b)ρ⊗ (a)ρ.It thus follows that(a)ρ=(b)ρ.Hence ≤ρsatisfies the antisymmetry.
To prove that≤ρis transitive,let(a)ρ≤ρ(b)ρand(b)ρ≤ρ(c)ρ.Then

and thus we have

which means that

Therefore,≤ρis a partially ordered relation on S/ρ.
Furthermore,let(a)ρ,(b)ρ,(c)ρ∈ S/ρ and(a)ρ≤ρ(b)ρ.We can show that

In fact,since(a)ρ,(b)ρ,(c)ρ∈ S/ρ,(a)ρ≤ρ(b)ρ,we have

Also,since(S/ρ,⊗)is a semigroup,we have


It implies that(c)ρ⊗(a)ρ≤ρ(c)ρ⊗(b)ρ.Similarly,(a)ρ⊗(c)ρ≤ρ(b)ρ⊗(c)ρ.We have thus shown that(S/ρ,⊗,≤ρ)is an ordered semigroup.This completes the proof.
Remark 3.3 If(S, ◦, ≤)is an ordered semihypergroup and ρ is a hypersemilattice strongly regular relation on S,then(S/ρ,⊗,≤ρ)is an ordered semigroup and(S/ρ,⊗)forms a semilattice.We call the ordered semigroup(S/ρ,⊗,≤ρ)the natural ordered semigroup induced by the hypersemilattice strongly regular relation ρ on S.
Definition 3.4 A hypersemilattice strongly regular relation ρ on an ordered semihypergroup(S,◦,≤)is called complete if a≤ b impliesfor any a,b∈S.
Definition 3.5 Let(S,◦,≤),(T,∗,≤1)be two ordered semihypergroups.A mapping f:S−→ T is called isotone if x,y∈S,x≤ y implies f(x)≤1f(y)in T.f is called a homomorphism if it is isotone and satisfies that

Theorem 3.2 Let(S,◦,≤)be an ordered semihypergroup and ρ a complete hypersemilattice strongly regular relation on S.Then the mapping

is a homomorphism.Here φ is called a natural mapping associated with ρ.
Proof. Suppose that ρ is a complete hypersemilattice strongly regular relation on an ordered semihypergroup S.By Theorem 3.1,(S/ρ,⊗,≤ρ)is an ordered semigroup,and,of course,is also an ordered semihypergroup.We can prove that φ is isotone.Indeed,let x,y ∈ S such that x ≤ y.It is enough to show that(x)ρ≤ρ(y)ρ.Since ρ is complete,we have.It implies that xρz for any z∈ x◦y.Hence we havefrom which we can deduce that(x)ρ≤ρ(y)ρ.Furthermore,let x,y ∈ S.Then
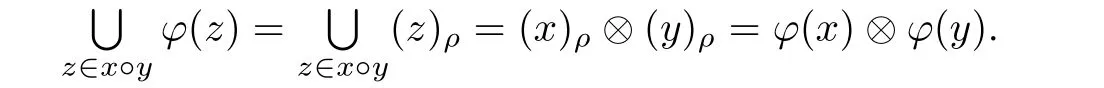
Therefore,φ is a homomorphism from S into S/ρ.
4 Hyper filters of Ordered Semihypergroups
In[10],Tang et al.introduced the concept of hyper filters of ordered semihypergroups.In the current section,we study mainly the properties of hyper filters of an ordered semihypergroup,and give several applications of hyper filters in ordered semihypergroups.
Definition 4.1[10]Let S be an ordered semihypergroup.A subsemihypergroup F of S is called a hyper filter of S if
(1)(a◦b)∩F ≠∅⇒a∈F and b∈F,∀a,b∈S.
(2)If a∈F and a≤b∈S,then b∈F.
Especially,if(S,◦,≤)is an ordered semigroup,then the hyper filters of S coincide with the filters of S defined in[15].
Lemma 4.1[10]Let S be an ordered semihypergroup and{Fi|i∈I}a family of left(resp.right)hyper filters of S.Thenis a left(resp.right)hyper filter of S ifwhere|I|≥2.
Lemma 4.2[10]Let{Fk|k∈I}be a family of hyper filters of an ordered semihypergroup S such that Fi⊆Fjor Fj⊆Fi,for all i,j∈I.Thenis a hyper filter of S,where|I|≥2.
The hyper filters of ordered semihypergroups can be characterized by completely prime hyperideals.
Theorem 4.1[10]Let S be an ordered semihypergroup and F a nonempty subset of S.Then the following statements are equivalent:
(1)F is a hyper filter of S;
(2)SF=∅or SF is a completely prime hyperideal of S,where SF is the complement of F in S.
Theorem 4.2 Let S be an ordered semihypergroup and{Ti|i∈I}a family of completely prime hyperideals of S.Thenis a completely semiprime hyperideal of S ifProof. Let Tibe a completely prime hyperideal of S for any i∈I.Assume thatThen,by Lemma 2.2,is a hyperideal of S.Moreover,we can show thatis completely semiprime.In fact,let a∈S be such that.Then


Hence,by hypothesis,a∈Tifor every i∈I.It thus follows thatTherefore,is a completely semiprime hyperideal of S.The proof is completed.
In the above theorem we have shown that every nonempty intersection of completely prime hyperideals of an ordered semihypergroup S is completely semiprime. But the nonempty intersection of completely prime hyperideals of S is not necessarily a completely prime hyperideal of S.We can illustrate it by the following example.
Example 4.1 We consider a set S:={a,b,c,d}with the following hyperoperation “◦”and the order“≤”:


We give the covering relation“≺”and the figure of S as follows:

Then(S,◦,≤)is an ordered semihypergroup(see[10]).We can easily verify that T1={a,b,d},T2={a,c,d}are completely prime hyperideals of S.But T1∩T2={a,d}is not a completely prime hyperideal of S.In fact,since(b◦ c)∩ {a,d}={a,d} ≠ ∅,but b∉{a,d}and c∉{a,d}.
As an application of Theorem 4.1,the following theorem is obtained.
Theorem 4.3 Let S be an ordered semihypergroup.Then the set of completely prime hyperideals of S is a chain under inclusion if and only if every nonempty intersection of completely prime hyperideals of S is a completely prime hyperideal of S.

Since Iαis a completely prime hyperideal of S for every i ∈ Λ,by Theorem 4.1,SIα(α ∈ Λ)is a hyper filter of S if SIα≠ ∅.Notice that the hypothesis implies that{Iα}α∈Λis a chain under inclusion.Thus,{SIα}α∈Λis also a chain under inclusion,and by Lemma 4.2,is a hyper filter of S,which implies that SI is a hyper filter of S.Therefore,I is a completely prime hyperideal of S by Theorem 4.1.
Conversely,let I1and I2be completely prime hyperideals of S.If there exist x,y∈S such that x∈I1I2and y∈I2I1,then x◦y⊆I1∩I2because I1and I2are hyperideals of S,and thus(x◦y)∩(I1∩I2)≠ ∅.By hypothesis,I1∩I2is a completely prime hyperideal of S.Consequently,we have x∈I1∩I2or y∈I1∩I2.Impossible.Therefore,we have I1⊆I2or I2⊆I1.In other words,the set of completely prime hyperideals of S is indeed a chain under inclusion.
Let S be an ordered semihypergroup and I a nonempty subset of S.We define a relation δIon S as follows:

It can be easily proved that δIis an equivalence relation on S(see[11]).Furthermore,we have the following lemma.
Lemma 4.3 Let S be an ordered semihypergroup and I a completely prime hyperideal of S.Then δIis a hypersemilattice strongly regular relation on S.
Proof. Let aδIb and c∈ S.Then we prove that.Indeed,since aδIb,we have a,b∈I or a,b∉I.If a,b∈I,then,since I is a hyperideal of S,we have c◦a⊆I and c◦b⊆ I.Hence,for every x∈ c◦a and y∈c◦b,we have xδIy.Thus,in this case,we have shown that.Let a,b ∉ I.We consider the following two cases.
Case 1.If c∈I,then,since I is a hyperideal of S,we have c◦a⊆I and c◦b⊆I.Thus
Case 2.Let c∉I.Then a,b,c∈SI.Since I is a completely prime hyperideal of S and I=S(SI),by Theorem 4.1,SI is a hyper filter of S.Thus we have c◦a⊆SI and c◦b⊆ SI.It implies that x,y ∉ I for every x ∈ c◦a and y ∈ c◦b.Thus we have xδIy,and.Similarly,we can show that.This proves that δIis a strongly regular relation on S.
Furthermore,let a,b∈S.Then we claim that.To prove our claim,it is enough to prove that for every x∈a◦b and y∈b◦a we have x,y∈I or x,y∉I.In fact,if x∈I and y∉I for some x∈a◦b and y∈b◦a,then y∈(b◦a)I⊆SI.By the above proof,SI is a hyper filter of S.Since y∈b◦a and y∈SI,we have a,b∈SI,and thus a◦b⊆ SI.Hence x ∈ SI,i.e.,x ∉ I.This is a contradiction.Similarly,if x ∉ I and y∈I for some x∈a◦b and y∈b◦a,then we can also obtain a contradiction.
Therefore,δIis a hypersemilattice strongly regular relation on S.This completes the proof.
Let now S be an ordered semihypergroup and A a nonempty subset of S.We denote

Clearly,Ω is not empty since S∈Ω.Let.It is clear that N(A)≠ ∅ because
A⊆N(A).By Lemma 4.1,N(A)is a hyper filter of S.Moreover,N(A)is the smallest hyper filter of S containing A.The hyper filter N(A)is called the hyper filter of S generated by A.For A={x},let N(x)denote the hyper filter of S generated by{x}.We denote by N the equivalence relation on S defined by N:={(x,y)∈S×S|N(x)=N(y)},and define by(x)Nthe N-class of S containing x(x∈S).
Theorem 4.4 Let S be an ordered semihypergroup.Then the following statements hold:
(1)N is a hypersemilattice strongly regular relation on S;
(2)N= ∩{δI|I ∈ CP(S)},where CP(S)is the set of all completely prime hyperideals of S.
Proof.(1)Let xNy and z∈ S.Then we prove that.Indeed,let a∈ z◦x and b∈z◦y.Since a∈N(a)and N(a)is a hyper filter of S,we have z∈N(a)and x∈N(a).Since x∈N(a)and N(x)=N(y),we have N(y)⊆N(a),i.e.,y∈N(a).Since z,y∈N(a),we have z◦y⊆N(a),and b∈N(a),which implies that N(b)⊆N(a).By symmetry,N(a)⊆N(b).Hence N(a)=N(b),i.e.,aNb.It thus follows that.Similarly,for any z∈S.Therefore,N is a strongly regular relation on S.
Thus N is a hypersemilattice strongly regular relation on S.
(2)Let(x,y)∈N.Then we prove that(x,y)∈δIfor any I∈CP(S).Indeed,if(x,y) ∉ δIfor some I ∈ CP(S),then x ∉ I and y ∈ I or x ∈ I and y ∉ I.Let x ∉ I and y∈I.Then∅≠SI⊆S.Since S(SI)(=I)is a completely prime hyperideal of S,by Theorem 4.1,SI is a hyper filter of S.Since x∈SI,we have N(x)⊆SI,and thus N(y)⊆SI,i.e.,y∈SI.It contradicts the fact that y∈I.Similarly,if x∈I and y ∉ I,we can also get a contradiction.This proves that N ⊆ ∩{δI|I ∈ CP(S)}.To show the inverse inclusion,let(x,y)∈ δIfor any I ∈ CP(S).Assume that(x,y) ∉ N.Then it can be easily shown that x∉N(y)or y∉N(x).Let x∉N(y).Then x∈SN(y).For the simplicity’s sake,we denote SN(y)by I′.Then I′≠ ∅.Since N(y)is a hyper filter of S,by Theorem 4.1,I′is a completely prime hyperideal of S.Thus we have I′∈ CP(S),x ∈ I′and y ∉ I′(since y ∈ N(y)),and(x,y) ∉ δI′,which contradicts the hypothesis.From y ∉ N(x),similarly,we get a contradiction.Hence(x,y)∈ N.We have thus shown that∩{δI|I∈ CP(S)}⊆ N.The proof is completed.
By Theorem 4.4 we have shown that

where CP(S)is the set of all completely prime hyperideals of S.A natural question is whether N is the least hypersemilattice strongly regular relation on S.The following example gives a negative answer to the above question.
Example 4.2 We consider a set S:={a,b,c,d}with the following hyperoperation “◦”and the order“≤”:

We give the covering relation“≺”and the figure of S as follows:

Then(S,◦,≤)is an ordered semihypergroup.We can easily show that N(a)=N(b)=N(c)=N(d)=S,and thus N=S×S.Now let

With a small amount of e ff ort one can verify that δ is a hypersemilattice strongly regular relation on S.Clearly,δ⊂ N.
By the above example we have shown that N is not the least hypersemilattice strongly regular relation on S.But we claim that N is the least complete hypersemilattice strongly regular relation on S.To prove this assertion,we first introduce the following definition.
Definition 4.2 Let S be an ordered semihypergroup and F a hyper filter of S.F is called a-maximal if F is maximal with respect to the property of not containing a∈S.
We denote all a-maximal hyper filters of S by val(a).
Theorem 4.5 Let S be an ordered semihypergroup.Then(x,y)∈N if and only if val(x)=val(y)for any x,y∈S.
Proof.Assume that(x,y)∈N.Then N(x)=N(y).Let F∈val(x).Clearly,x∉F.Then we have y∉F.Indeed,if y∈F,then y∈N(y)⊆F.Hence x∈N(x)=N(y)⊆F,which is a contradiction.Furthermore,we claim that F ∈val(y).In fact,if F ∉val(y),then,by Zorn’s Lemma,there exists a hyper filter F1of S such that y ∉ F1and F ⊂ F1.If x ∉ F1,we have a contradiction since F∈val(x).If x∈F1,then we have y∈N(y)=N(x)⊆F1.Impossible.We have thus shown that val(x)⊆val(y).By symmetry,we can prove that val(y)⊆val(x).
Conversely,let x,y∈S.If val(x)=val(y),then x∈N(y).Indeed,if x∉N(y),then,by Zorn’s Lemma,there exists an F ∈ val(x)such that N(y)⊆ F,and we get y ∈ F,which contradicts the fact that val(x)=val(y).By symmetry,we have y∈N(x).Thus N(x)=N(y),which means that(x,y)∈N.
Theorem 4.6 Let S be an ordered semihypergroup.Then N is a complete hypersemilattice strongly regular relation on S.
Proof. By Theorem 4.4,N is a hypersemilattice strongly regular relation on S.Furthermore,we can prove that N is complete.In fact,let x,y∈S such that x≤y.Since N(x)is a hyper filter of S and N(x)∋x≤y,we have y∈N(x).Since x,y∈N(x),we have x◦y⊆N(x).Hence,for any z∈x◦y,we have z∈N(x),that is,N(z)⊆N(x).On the other hand,since N(z)is a hyper filter of S,z∈x◦y and z∈N(z),we have x∈N(z),and N(x)⊆N(z).Hence N(x)=N(z),that is,xNz.It thus follows that.Therefore,N is a complete hypersemilattice strongly regular relation on S.
Lemma 4.4 Let(S,◦,≤),(T,∗,≤1)be ordered semihypergroups and f:S −→ T a homomorphism.If F is a hyper filter of T and f−1(F) ≠ ∅,then f−1(F)is a hyper filter of S.
Proof.Let x,y∈f−1(F).Then f(x),f(y)∈F.Since f:S−→T is a homomorphism and F is a hyper filter of T,we have.Thus for any z∈ x◦y we have f(z)∈ F,i.e.,z∈ f−1(F).Hence x◦y⊆ f−1(F),that is,f−1(F)is a subsemihypergroup of S.
Let x,y ∈ S be such that x ◦y∩ f−1(F)≠ ∅.Then we claim that x ∈ f−1(F)and y∈ f−1(F).To prove our claim,let z∈x◦y such that z∈ f−1(F).Then f(z)∈F.Since z∈x◦y,by hypothesis we have.Hence f(x)∗f(y)∩F ≠ ∅,which implies that f(x)∈ F and f(y)∈ F since F is a hyper filter of T.Thus x∈f−1(F)and y∈f−1(F).
Furthermore,let x∈f−1(F),x≤ y∈S.Then,by hypothesis,f(x)∈F and f(x)≤1f(y).Since F is a hyper filter of T and f(x)∈F,we have f(y)∈ F,that is,y∈f−1(F).
Therefore,f−1(F)is a hyper filter of S.
Lemma 4.5 Let(S,◦,≤)be an ordered semihyergroup and ρ a complete hypersemilattice strongly regular relation on S.If(x,y)∈ N on S,then((x)ρ,(y)ρ)∈ N on S/ρ.
Proof. Assume that N((x)ρ) ≠N((y)ρ).Then(x)ρ∉ N((y)ρ)or(y)ρ∉ N((x)ρ).Let(x)ρ∉ N((y)ρ).Similar to the proof of Theorem 4.5,there exists an F ∈ val((x)ρ)such that(y)ρ∈ F.Let φ:S −→ S/ρ be a natural mapping associated with ρ.By Theorem 3.2,φ is a homomorphism.Thus,by Lemma 4.4,φ−1(F)is a hyper filter of S,and x ∉ φ−1(F),y ∈ φ−1(F).By Zorn’s Lemma,there exists an x-maximal hyper filter which contains y,and thus val(x)≠val(y).By Theorem 4.5,we can conclude that(x,y)∉N.Impossible.From(y)ρ∉ N((x)ρ),similarly,we get a contradiction.Therefore,N((x)ρ)=N((y)ρ),and((x)ρ,(y)ρ) ∈ N on S/ρ.
Lemma 4.6[3]Let(S,·,≤)be an ordered semigroup and the semigroup(S,·)form a semilattice.Then N(x)=[x)for any x∈S,where N(x)is the filter of S generated by x.
Theorem 4.7 Let S be an ordered semihypergroup.Then N is the least complete hypersemilattice strongly regular relation on S.
Proof. By Theorem 4.6,N is a complete hypersemilattice strongly regular relation on S.Furthermore,we can show that N is the least complete hypersemilattice strongly regular relation on S.Indeed,let ρ be any complete hypersemilattice strongly regular relation on S,and let x,y ∈ S such that(x,y) ∈ N.By Lemma 4.5,((x)ρ,(y)ρ) ∈ N on S/ρ,that is,N((x)ρ)=N((y)ρ).Since ρ is a hypersemilattice strongly regular relation on S,by Remark 3.3,(S/ρ,⊗,≤ρ)is an ordered semigroup and(S/ρ,⊗)forms a semilattice.Thus,by Lemma 4.6,we have N((x)ρ)=[(x)ρ)and N((y)ρ)=[(y)ρ).Hence[(x)ρ)=[(y)ρ),which implies that(x)ρ=(y)ρ.It thus follows that(x,y)∈ ρ,and N ⊆ ρ.
 Communications in Mathematical Research2019年2期
Communications in Mathematical Research2019年2期
- Communications in Mathematical Research的其它文章
- Holomorphic Curves into PN(C)That Share a Set of Moving Hypersurfaces
- Consequence Operators and Information Algebras
- Existence of Solutions for Fractional Differential Equations with Conformable Fractional Differential Derivatives
- Hyers-Ulam Stability of First Order Nonhomogeneous Linear Dynamic Equations on Time Scales
- Volume Di ff erence Inequalities for the Polars of Mixed Complex Projection Bodies
- Long-time Dynamics for Thermoelastic Bresse System of Type III
