Hyers-Ulam Stability of First Order Nonhomogeneous Linear Dynamic Equations on Time Scales
Shen Yong-hongand Li Yong-jin
(1.School of Mathematics and Statistics,Tianshui Normal University,Tianshui,Gansu,742100)
(2.Department of Mathematics,Sun Yat-Sen University,Guangzhou,510275)
Communicated by Li Yong
Abstract:This paper deals with the Hyers-Ulam stability of the nonhomogeneous linear dynamic equation x∆(t)−ax(t)=f(t),where a∈R+.The main results can be regarded as a supplement of the stability results of the corresponding homogeneous linear dynamic equation obtained by Anderson and Onitsuka(Anderson D R,Onitsuka M.Hyers-Ulam stability of first-order homogeneous linear dynamic equations on time scales.Demonstratio Math.,2018,51:198–210).
Key words:Hyers-Ulam stability,∆-derivative,time scale,linear dynamic equation
1 Introduction
In 1940,Ulam[1]posed the following problem concerning the stability of group homomorphisms:Under what conditions can a solution of a perturbed equation be close to a solution of the original equation.The following year,Hyers[2]solved this type of stability problem for the case of approximately additive mappings in Banach spaces.Afterwards,the result of Hyers was generalized by Rassias[3]for linear mappings by considering an unbounded Cauchy difference.Since then,there has been a great interest in the Hyers-Ulam stability(HUS)of functional and differential equations.For more detailed results,the reader can refer to these monographs(see[4]–[8]and the references therein).
For an n-th order differential equation

where I is a nonempty open interval I of R.We say that the equation(1.1)has Hyers-Ulam stability(HUS)if and only if there is a constant K>0 with the property:Given a ε>0,if an n-time differentiable function y:I→R satisfies

then there exists a solution x:I→ R of(1.1)such that|x(t)−y(t)|≤ Kε for all t∈I.Such a constant K is called an HUS constant for the equation(1.1)on I.
In 1998,Alsina and Ger[9]proved the Hyers-Ulam stability of the differential equation

and obtained an HUS constant 3 on I.Subsequently,Miura et al.[10]and Takahasi et al.[11]considered the Hyers-Ulam stability of first order linear differential operators in a complex Banach space.As a special case,these results showed that the differential equation

has the Hyers-Ulam stability with a HUS constantMoreover,if given a solution ϕ(t)of the perturbed equation,then the solution x(t)of the original equation satisfying

is unique.In 2017,Onitsuka and Shoji[12]further studied the Hyers-Ulam stability of the equation

from a different perspective.Under the assumption that a differentiable function ϕ(t)satisif es

they constructed an explicit solution x(t)of the corresponding equation

satisfying

Also,Onitsuka[13]discussed the in fluence of the constant step size h on Hyers-Ulam stability of the first-order homogeneous linear difference equation

on the uniformly discrete time scale hZ.Meantime,Onitsuka[14]further investigated the Hyers-Ulam stability of the first-order nonhomogeneous linear difference equation


on hZ.Recently,Anderson and Onitsuka[15]studied the Hyers-Ulam stability of the first order homogeneous linear dynamic equation on time scales.It is clear that this work can be regarded as a unification of the previous results obtained from[12]–[14].In addition,Shen[16]established the Ulam stability of the first order linear dynamic equation and its adjoint equation on a finite time scale.
The main purpose of the present paper is to consider the Hyers-Ulam stability of the first order nonhomogeneous linear dynamic equation

with the coefficients a∈R+on time scales.Throughout this paper,we assume f∈Crd(T,R).
2 Preliminaries
For the sake of completeness,in this section,we review some related notions and fundamental results which are derived from[15]and[17]–[19].Let R,Z and N0denote the set of all real numbers,the set of all integers and the set of all nonnegative integers,respectively.
A time scale T is an arbitrary nonempty closed subset of R.Clearly,R,Z and N0are typical examples of time scales.
Let T be a time scale.For t∈ T,the forward jump operator σ:T→T and the backward jump operator ρ:T → T can be defined,respectively,by

where we put inf∅=supT and sup∅=inf T.A point t∈T is called right-scattered,rightdense,left-scattered and left-dense if σ(t)>t, σ(t)=t,ρ(t) The set Tκ=T{M}if T has a left-scattered maximum M.Otherwise,Tκ=T. Let f:T→R and let t∈Tκ.We say that f is∆-differentiable at t provided there exists a number(denoted as f∆(t))with the property that given any ε >0 there is a neighborhood U of t such that Furthermore,f is said to be∆-differentiable on Tκif f∆(t)exists for all t∈ Tκ.Accordingly,the function f∆:Tκ→R is then called the∆-derivative of f on T.In particular,if T=R,then f∆=f′(the usual derivative),if T=Z,then f∆= ∆f(the usual forward difference),and if T=qN0(q>1),then f∆=Dqf(the usual Jackson derivative). A function f:T→R is called rd-continuous provided it is continuous at all right-dense points of T and its left-sided limits exist( finite)at left-dense points of T.For simplicity,we denote by Crd(T)=Crd(T,R)the set of all rd-continuous functions on T.In addition,a function F:T→ R is called an antiderivative of f:T→ R if F∆(t)=f(t)for all t∈Tκ.For a rd-continuous function f:T→R,the(Cauchy)integral can be well defined by because each rd-continuous function possesses an antiderivative. A function p:T → R is regressive provided 1+ µ(t)p(t) ≠0 for all t∈ Tκ.The set of all regressive and rd-continuous functions f:T→R is denoted by R=R(T)=R(T,R).Especially,we write p∈R+if 1+µ(t)p(t)>0,and p∈R−if 1+µ(t)p(t)<0 for all t∈Tκ. For p,q∈R,the circle plus⊕of p and q is defined by Meantime,the circle minus⊖is defined by In essence,the pair(R,⊕)is an Abelian group.Then the inverse element of p with respect to⊕is Let p∈R and let t0∈T.The generalized exponential function ep(t,t0)is defined by the unique solution of the initial valued problem Some useful properties of the generalized exponential function are collected below. Theorem 2.1[17]Assume p,q∈R and t,s,r,t0∈T.Then Remark 2.1 From(iv)and(vii)of Theorem 2.1,it easily follows that holds for all t∈T. Theorem 2.2 Assume p∈R−and t,t0∈T.Then Proof. Since p∈ R−,i.e.,1+µ(t)p(t)<0,we know thatµ(t)>0 for all t∈ T.This means that each point t in Tκis right-scattered.Then,we have According to the∆-derivative product rule,we can obtain where the last equality follows from the fact that This completes the proof. Theorem 2.3[15]Let ε>0 be a given arbitrary constant and fix t0∈ T.Suppose that a∆-differentiable function ϕ:T→R satisfies where a≠0.Then one of the following holds: (i)If a>0 and τ∗:=maxT exists,then any solution x(t)of(1.2)with|ϕ(τ∗)−x(τ∗)| (ii)If a>0 and maxT does not exist,thenexists,and there exists a unique solution of(1.2)such that|ϕ(t)− x(t)|≤for all t∈T; (iii)If a ∈ R+with a<0 and τ∗:=minT exists,then any solution x(t)of(1.2)withsatisfies|ϕ(t)− x(t)| (iv)If a∈R+with a<0 and minT does not exist,thenexists,and there exists a unique solution of(1.2)such that|ϕ(t)− x(t)|≤for all t∈T. Remark 2.2 Notice that Theorem 2.3,which is based on Lemma 3.4 in[?],plays a key role in proving the Ulam stability of first order linear dynamic equations with the coefficient a∈R+.However,under the condition a∈R−,it is difficult to establish a similar equivalence relationship from Theorem 2.2.Consequently,it is still an open question how to establish the similar stability results of first order linear dynamic equations with the coefficient a∈R−. In this section,we consider the Hyers-Ulam stability of the first order nonhomogeneous linear dynamic equation with a constant coefficient a∈R+,which include the time scale T=R,T=Z and T=qN0as important special cases. Theorem 3.1 Let ε>0 be a given arbitrary constant and fix t0∈ T.Suppose that a∆-differentiable function ϕ:T→R satisfies for all t∈ Tκ,where a ≠0.Then one of the following holds: (i)If a>0 and τ∗:=maxT exists,then any solution x(t)of(1.3)with|ϕ(τ∗)−x(τ∗)| (ii)If a>0 and maxT does not exist,then exists,and there exists a unique solution of(1.3)such that|ϕ(t)− x(t)|≤for all t∈T; (iii)If a ∈ R+with a<0 and τ∗:=minT exists,then any solution x(t)of(1.3)withsatisfiesfor all t∈T; (iv)If a∈R+with a<0 and minT does not exist,then exists,and there exists a unique solution of(1.3)such that|ϕ(t)− x(t)|≤for all t∈T. Proof. Set Then,we can obtain that This shows that u(t)is a solution of(1.3)on T.Therefore,we get By the assumption,we have First we have to prove(i).Let x(t)be any solution of(1.3)satisfying Set v(t)=x(t)−u(t)for t∈T.Since we know that v(t)is a solution of(1.2).By the condition,we can obtain By the assertion(i)in Theorem 2.1 and(3.1),we can infer that which implies that This is to say,the assertion(i)is true. Using the same argument,the assertion(iii)can also be proved. Next we need to verify(ii).From(3.1)and Theorem 2.3(ii),we know that exists,and there exists a unique solution of(1.2)such that Set x(t)=u(t)+w(t).Then,we get which means that x(t)is a solution of(1.3).Furthermore,we know that is exactly one solution of(1.3)such that The assertion(iv)can be proved in a similar way as shown before.This completes the proof. Remark 3.1 Theorem 3.1 shows that,if a>0 or a∈R+with a<0,(1.3)has Hyers-Ulam stability with an HUS constanton T. Corollary 3.1 If a>0,then the differential equation x′(t)−ax(t)−f(t)=0 has Hyers-Ulam stability with a HUS constanton R.Furthermore,given ε>0,if a function ϕ:R→R satisfies then exists,and there exists exactly one solution of the foregoing differential equation such that|ϕ(t)−x(t)|≤for all t∈R,where t∈R|0is an arbitrary fixed point. Remark 3.2 when a<0,the result of Corollary 3.2 is still true if we replace t→∞by t→ −∞ in the limit formula above. Corollary 3.2 If a>0,then the difference equation has Hyers-Ulam stability with an HUS constanton Z.Furthermore,given ε>0,if a function ϕ :Z→R satisfies then exists,and there exists exactly one solution of the foregoing difference equation such thatfor all t∈Z with t>t0,where t0∈Z is an arbitrary fixed point. Corollary 3.3 If−1 has Hyers-Ulam stability with an HUS constanton Z.Furthermore,given ε>0,if a function ϕ :Z→R satisfies for all t∈Z,then exists,and there exists exactly one solution of the foregoing difference equation such thatfor all t∈Z with t>t,0where t0∈Z is an arbitrary fixed point. Corollary 3.4 If a>0,then the q-difference equation Dqx(t)−ax(t)−f(t)=0 has Hyers-Ulam stability with an HUS constanton qN0.Furthermore,given ε>0,if a function ϕ:qN0→R satisfies then exists,and there exists exactly one solution of the foregoing difference equation such thatfor all t∈qN0with t>t0,where t0∈qN0is an arbitrary fixed point.















3 The Main Results












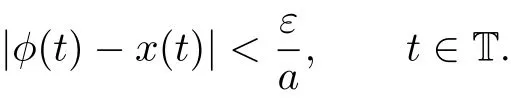
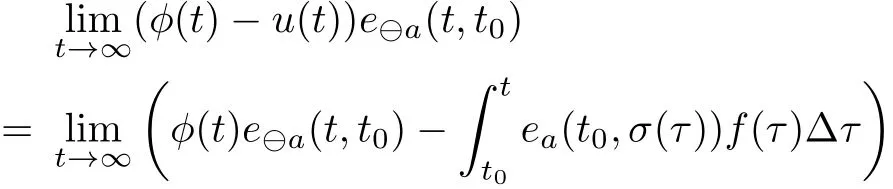









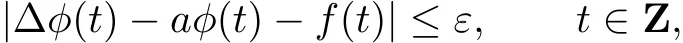
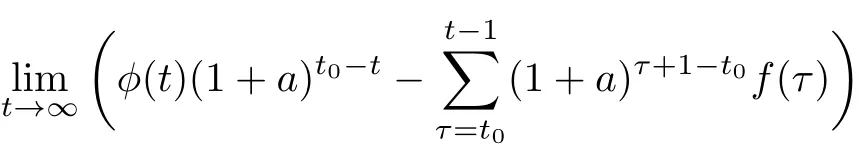








 Communications in Mathematical Research2019年2期
Communications in Mathematical Research2019年2期
