地震作用下孔隙水压力对边坡动力稳定性的影响
(1.河海大学 水利水电学院,南京 210098;2.长江水利委员会 长江勘测规划设计研究院,武汉 430010)
1 研究背景
在我国,自然边坡和人工边坡数量多、分布广,一旦发生滑坡会造成极大的危害,因此边坡稳定性分析问题一直是学术界和工程界关注的热点。大量工程实例表明,水的作用常是造成边坡失稳的重要因素,开展相关研究对社会生产和生命安全具有十分重要的意义。汪自力等[1]引入渗透力代替孔隙水压力,直接采用渗流分析模型连续求解渗流作用下的边坡稳定;谢罗峰等[2]通过试验研究了水位降落下的非稳定渗流场对边坡稳定性的影响,发现渗流方向是稳定性分析的关键;任德斌等[3]采用拟静力法和降强法研究了降雨和地震作用下土坡稳定性的变化规律,认为降雨及地震是影响边坡稳定性的敏感因素;宋波等[4]提出将地震和地下水影响直接叠加会低估其对边坡稳定性的影响,与室内振动台试验结果一致;黄帅等[5]也通过数值模拟和室内试验发现动孔压的存在会使得边坡在受较大动应力时破坏加速。上述结论表明在两相介质边坡的稳定性分析中,水是一个至关重要的因素,如何考虑孔隙水压力的变化及影响是决定分析结果准确性的关键因素。
本文以有限元法和极限平衡法为基础,以某水库堤坝为研究对象,通过耦合渗流场和震动场,讨论了地震作用下的非稳定渗流场及土体动力响应。重点考虑了非稳定渗流和地震荷载作用下激发的超孔隙水压力的变化及其对坡体稳定性的影响,为研究滑坡问题提供了一定的参考。
2 基本理论
2.1 饱和-非饱和土体非稳定渗流场分析
2.1.1 达西定律
土体的达西定律表达式为
v=ki。
(1)
式中:v为渗透速度;k为渗透系数;i为水力梯度。
在非饱和土中,渗透系数k会受土体含水量及孔隙水压力的影响[6],不再是一个固定常数。该值可用Fredlund-Xing模型进行预测,即用土-水特征曲线表示基质吸力和体积含水率之间的关系[7],其表达式为
(2)
式中:θw为体积含水率;θs为饱和体积含水率;φ为基质吸力;a为进气值;n为当基质吸力超过土的进气值时土中流出率函数的土性参数;m为残余含水量函数的土性参数。
渗透系数曲线可以表达为
kw=ksΘp。
(3)

2.1.2 有限元控制方程
二维渗流场的一般控制微分方程可以表示为:
(4)
(5)
式中:H为总水头;kx为x方向的渗透系数;ky为y方向的渗透系数;Q为施加的边界流量;uw为孔隙水压力;γw为水的重度;x为水平方向距离;y为高程。
在饱和土体中,θw为一定值;在非饱和土体中,θw随土体性质和应力状态的不同而不同。为简化θw的求解,本文假设如下:①不考虑土体的加载及卸载;②非饱和土中孔隙气应力为常量。此时,体积含水率θw可以表示为孔隙水压力uw的函数,即
∂θw=mw∂uw。
(6)
式中mw为储水曲线的斜率。
将式(5)、式(6)代入式(4),得
(7)
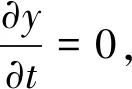
(8)
2.2 动力作用下超孔隙水压力计算
Seed等[8-9]提出了振动孔隙水压力的应力模型,其表达式为
(9)

2.3 土体滑坡的稳定性分析
边坡稳定计算时采用Fredlund等[11]提出的非饱和土抗剪强度公式,即:
τ=c′+(σn-ua)tanφ′+(ua-uw)tanφb; (10)
(11)
式中:τ为非饱和土抗剪强度;c′为有效黏聚力;φ′为有效内摩擦角;σn为条块底面中心法向力;ua为孔隙气应力;uw为孔隙水压力;σn-ua为净法向应力;ua-uw为基质吸力;φb为基质吸力对抗剪强度的贡献所对应的摩擦角;σx为底面中心x方向的总应力;σy为底面中心y方向的总应力;τxy为底面中心的剪应力;α为x正方向正应力间的夹角。
有限元应力法中将边坡稳定系数Fs定义为在某一滑面上抗剪力Tf和下滑力T的比值,可表达为
(12)
(13)
式中:τm为下滑剪应力;l为条块底面长度。
3 考虑孔隙水压力影响的边坡稳定性分析方法
3.1 计算模型及边界条件
本文以某水库堤坝为研究对象,坝高44 m,坝基宽沿顺河向350 m,坝顶宽度16 m,上游面坡比为1∶2.5,下游面坡比为为1∶2.55。上游水位33 m,下游设排水沟,水位和坝基顶部齐平。图1给出了模型的几何尺寸、特征点位置及有限元网格剖分图,计算单元选取四边形耦合三角形,共有4 237个节点和4 141个单元。为保证结果的准确性,本文选择对坡面部分局部加密。
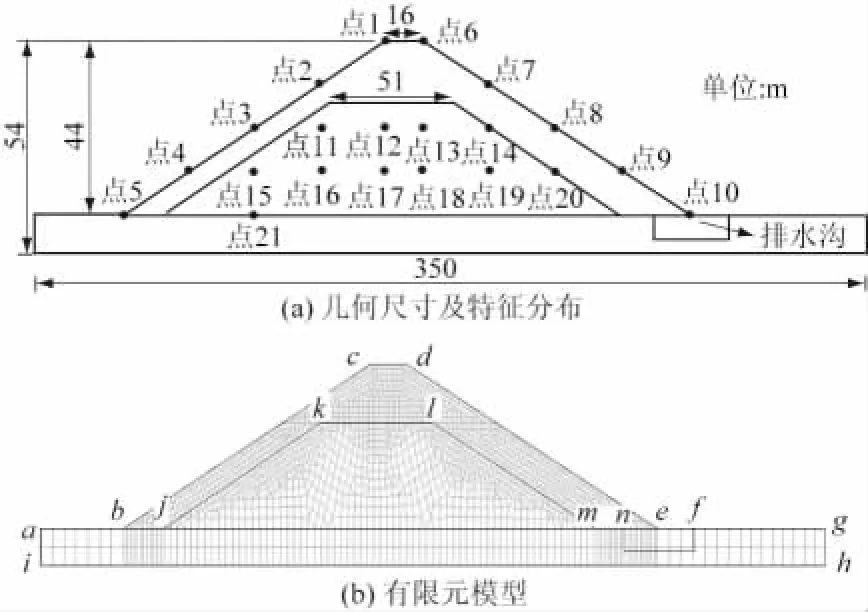
图1 堤坝几何尺寸及有限元计算模型Fig.1 Geometric dimensions of dam and finiteelement model of dam
边界条件如下:①ab,bc为入渗边界,在稳定渗流分析时按常水头边界处理,总水头值为33 m;②nf为出流边界,按压力水头为0的定边界条件处理;③动力分析时将基岩周围当作固定边界处理,ai和gh仅在x方向施加固定约束,ih在x,y方向均施加固定约束。
3.2 土体参数
本算例中,该堤坝坝壳为黏质砂土,坝内为中密砂,坝基材料为花岗岩,选取的土层计算参数如表1所示。在非饱和渗流分析时,选用Fredlund-Xing模型估算非饱和土中渗透系数随基质吸力的变化,得到渗透系数曲线及土-水特征曲线,如图2所示。在动力分析时,采用等效线性模型,土体动力特性如图3所示。

表1 土层计算参数Table 1 Calculation parameters of soil strata

图2 渗透系数曲线及土-水特征曲线Fig.2 Permeability coefficient curve and soil-watercharacteristic curve

图3 土体动力特性参数Fig.3 Dynamic parameters of soil mass
3.3 数值分析方法
本文选用的数值分析软件为GeoStudio,通过耦合SEEP/W,QUAKE/W,SLOPE/W等模块分别进行渗流分析、动力分析和边坡稳定性分析,主要步骤如下:
(1)以SEEP/W模块中稳态渗流分析结果作为静态分析的初始条件,得到初始状态下的孔隙水压力分布场。
(2)以QUAKE/W模块中的初始静态分析结果作为地震动分析的初始条件。对基岩周围施加固定约束,输入水平地震动曲线后采用时程分析法,得到地震期间每一瞬时的地震响应以及孔隙水压力分布情况等。
(3)以每一瞬时的孔隙水压力分布场作为SLOPE/W模块中边坡静动力稳定性分析的初始条件。在坡面上选定滑动面进出范围,选用Spencer刚体极限平衡法或有限元法等进行边坡稳定性分析,求解最危险滑块体位置及最小安全系数等。
4 孔隙水压力对边坡动力稳定性影响分析结果
图4给出了稳定渗流条件下孔隙水压力的分布情况,最大孔隙水压力约400 kPa,最大基质吸力约200 kPa。分别对坝体上下游作稳定性分析,得到结果如图5所示,蓝线表示浸润线位置,绿色区域表示可能存在的最危险滑块位置。此时该堤坝上下游均处于稳定状态,无滑坡危险。

图4 稳定渗流场下孔隙水压力分布情况Fig.4 Distribution of pore water pressure understeady seepage field

图5 稳定渗流场下边坡稳定性分析Fig.5 Stability analysis of slopes under steadyseepage field
边坡破坏主要受到水平地震动的影响,因此计算中只输入水平向地震波,见图6。地震历时14 s,动峰值加速度为0.4g,相当于地震基本烈度Ⅸ度。
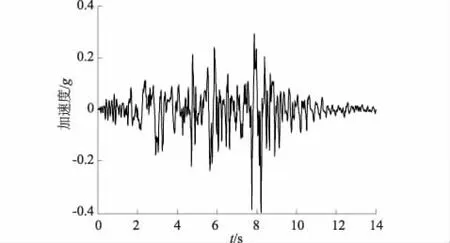
图6 地震波时程曲线Fig.6 Time history of seismic wave
以图1所示特征点为例,考虑地震作用下坝内各点的地震响应及地震激发的孔压变化情况,结果如图7—图9所示。
图7表明在地震作用期间,坝内浸润线围绕静力条件下稳态渗流场中的浸润线上下波动,未有显著变化。

图7 地震作用下浸润线变化示意图Fig.7 Changes of phreatic line under earthquake
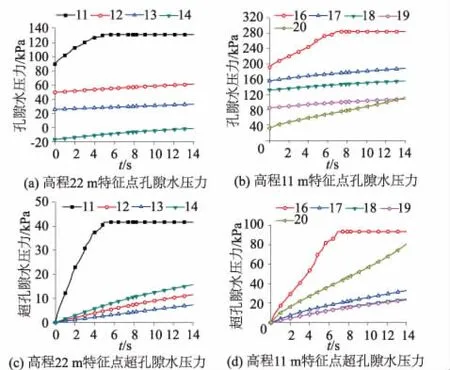
图8 地震作用下特征点孔隙水压力发展情况Fig.8 Development of pore water pressure atcharacteristic points under seismic action
图8反映了各特征点的孔隙水压力发展情况,发现规律如下:①从超孔压的增长过程来看,位于同一高程的坝内各点在震动期间满足临水面超孔压>背水面超孔压>坝中超孔压。这是因为坝中点有效固结应力较大,因此坝中点的剪应力比比较小,根据图3(b)循环函数可知其对应的液化破坏振次较大,会产生较小的超孔压,相应的超孔压增长速率也较小;而临水面点有效固结应力较小,则会带来较大的超孔压和较快的增长速率。②从孔压的数值变化来看,震前和震动期间都基本满足临水面孔隙水压力>坝中孔隙水压力>背水面孔隙水压力。这是因为在震动发生前,临水面点处于饱和状态,孔压较大;背水面点孔压最小,甚至为负(即基质吸力)。因此,在稳定渗流场下孔压满足临水面>坝中>背水面。虽然在震动期间,临水面超孔压>背水面超孔压>坝中超孔压,但是背水面超孔压的增值有限,因此背水面最终孔压仍比坝中要小,孔压关系仍保持临水面>坝中>背水面。
以上分析以地震荷载和孔隙水压力的耦合效应为基础,不仅考虑了孔隙水压力的影响,还考虑了动力荷载所激发的孔压变化的影响。地震结束时刻边坡稳定性分析如图9所示;在不考虑这种耦合关系时可使用拟静力法来求解该堤坝的地震响应,如图10所示;在完全不考虑水的影响时,可将土体作为单相介质求解该堤坝的地震响应,如图11所示;3种分析条件下边坡安全系数时程变化曲线如图12所示。

图9 考虑地震荷载及孔隙水压力耦合效应时边坡稳定性分析(t=14 s)Fig.9 Slope stability analysis in consideration ofthe coupling effect of seismic load and pore waterpressure(t=14 s)

图10 拟静力法求解的边坡动力稳定安全系数Fig.10 Result of dynamic stability safety factor ofslope obtained by pseudo-static method

图 11 不考虑孔压下边坡稳定性分析 (t=14 s)Fig.11 Slope stability analysis in no consideration ofpore water pressure (t=14 s)

图12 边坡安全系数时程变化曲线 (Spencer法)Fig.12 Time history curves of slope safety factorduring earthquake action by Spencer’s method
由图9—图11可知:①从滑面的形状和位置来看,考虑孔隙水压力但不考虑地震荷载和孔隙水压力的耦合作用时,易发生浅层滑动,且滑动面较平坦;考虑了两者的耦合作用时,滑面位置要明显深入许多,易发生深层滑动;②从瞬时安全系数来看,完全不考虑孔隙水压力时,安全系数偏大,高估了堤坝的抗震能力;而考虑孔隙水压力及其与地震荷载的耦合效应时,安全系数较小,表明这种耦合效应不可忽略。
分析上下游边坡的安全系数时程曲线,由图12可知:①不考虑孔隙水压力的情况下安全系数始终较大,考虑了孔隙水压力后则大幅下降(无论是否再考虑耦合效应),这表明孔压是影响边坡稳定性的重要因素。②地震初期边坡的稳定安全系数满足不考虑孔压时>考虑孔压及耦合效应时>不考虑耦合效应时,震后期关系则变为不考虑孔压时>不考虑耦合效应时>考虑孔压及耦合效应时。这表明地震荷载和孔压的耦合效应实际上反映了动力作用下孔压的累积性,且这种累积效应常常是影响边坡失稳的决定性因素。③根据刘汉龙等[12]对边坡失稳的判断依据可得边坡稳定性评价结果,如表2所示。考虑了孔压但不考虑耦合效应实际上是没有考虑动力作用下孔压的累积性,在震初期夸大了水的影响,而在震后期则低估了这一点;完全不考虑孔压则会大大高估堤坝的抗震稳定性。

表2 边坡抗震稳定性评价结果Table 2 Assessment results of seismic stability of slopes
以上结果表明:考虑耦合效应反映了边坡稳定性状态受地震过程的影响,实际也就是边坡失稳是一个量变引起质变的过程,当孔压累积到一定程度以后会对边坡稳定性起到至关重要的作用。由图13可知以上结论与采用的边坡稳定分析方法无关,对刚体极限平衡法和有限元分析方法均成立。对比图12和图13还可发现,地震作用期间下游侧边坡安全系数要始终大于上游侧边坡,这是因为下游侧边坡中部分土体处于非饱和状态,而非饱和土体中的基质吸力对边坡稳定性有利。
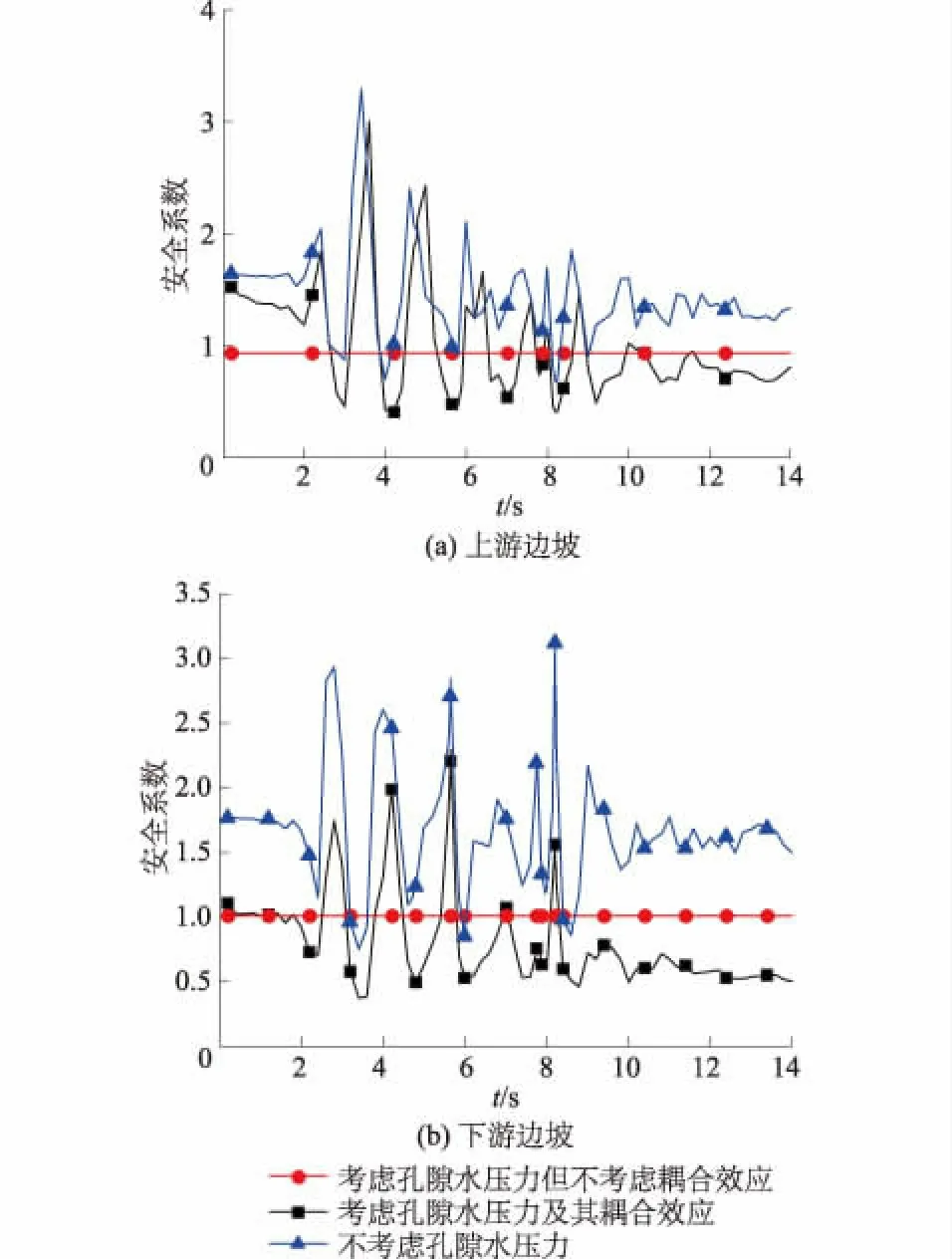
图13 边坡安全系数时程变化曲线 (FEM法)
Fig.13 Time history curves of slope safety factor underearthquake action by FEM
5 结 论
本文研究了孔隙水压力对边坡动力稳定性的影响,重点从地震作用激发的孔压变化着手,分别计算了坝坡的浸润线、坡内孔压分布、特征点孔压发展情况及安全系数时程变化等,基于本文算例得到如下结论。
(1)地震作用会激发超孔隙水压力的增长,坝上同一高程点的超孔压及其增长速率满足:临水面>背水面>坝中。地震荷载和孔压变化的耦合效应实际上反映了动力作用下孔压的累积性,且这种累积效应常常是影响边坡稳定的决定性因素。
(2)从滑面的形状和位置来看,不考虑地震荷载和孔隙水压力的耦合作用时,易发生浅层滑动,且滑动面较平坦;考虑了两者的耦合作用时,滑面位置要明显深入许多,易发生深层滑动。
(3)从安全系数来看,不考虑孔压影响时会高估堤坝的抗震稳定性;考虑孔压但忽略耦合效应时则不能真实反映水的影响;既考虑孔压又考虑该耦合效应时表明动力作用下孔压累积到一定程度以后会对边坡失稳起到至关重要的作用。

