基于GAN的天文图像生成研究

张光华, 王福豹, 段渭军

(西北工业大学 电子信息学院, 陕西 西安 710072)

图像生成技术是根据已知信息生成图像的过程、方法和算法的总称，它在过去的三十年间得到了飞速的发展并被应用于各种场景。Cohen等在1988年提出了一种基于动态计算结构因子的辐射度算法，首次将辐射度应用在图像生成领域[1]。Yoshio等在1998年通过视频流速全向图像采集和从全向视频流中实时生成图像解决了远程视频传输的延时问题[2-3]。近年来，随着卷积神经网络(CNN)在图像生成与处理领域应用研究的不断深入[4]，涌现出了很多使用CNN进行图像生成的方法。例如Yann等人利用CNN的多层反向传播结构对于复杂的、高纬度的、非线性图的学习能力，将CNN用于图像、语音和时间序列的处理中[5-6]。Zhang等利用图像的深度信息来生成立体图像[7]，其核心思想是采用非对称滤波器对图像的深度图进行预处理从而消除深度图中目标边界的非平滑变化。Park等采用视差估计的方法来进行三维图像的生成[8]。

2014年，Goodfellow等提出了生成对抗网络[9]，并迅速成为最流行的深度学习算法之一，在图形生成、图像分类、图像识别等领域展现出了强大的力量。GAN包含2个部分，一个是生成器，一个是鉴别器。它的优点是能够让生成器和鉴别器在对抗中自动获得最优的结果。这种方法的核心是利用CNN的多层卷积对目标图像进行特征提取，然后根据目标图像的像素概率密度分布特点进行重构，再将重构图像与目标图像进行对比后不断调优[10-11]。GAN将图像生成技术带到了全新的高度，在GAN被提出之后，许多领域的图像生成模型都采用了GAN的基本结构并对其进行了各种各样的改进[12-20]。

生成高分辨率的星系与恒星图像对预测未知恒星与星系，帮助人们了解宇宙有着重要的意义。 GAN能够利用简单的结构生成较为清晰的图像，然而它的缺点是整个模型较难训练稳定，极易出现过拟合或是欠拟合的情况。针对这种情况，研究人员提出了多种方法来稳定训练，例如：批归一化[21]、整流线型单元[22]、随机抛弃方法[23]等。这些方法在一定程度上稳定了GAN的训练过程，然而到目前为止还没有一个最有效的方法能够保证GAN在训练中的稳定，尤其是当目标图像分辨率较高时。目前使用GAN进行图像生成所使用的训练图像绝大部分是人脸或是景观图像，而对于来自于宇宙的星系，恒星等图像的生成却鲜有关注。要生成高分辨率的星系与恒星图像，必须进一步研究和提高GAN的稳定性。

本文针对GAN应用在生成星系以及恒星图像上存在的不稳定问题，对GAN的结构进行了优化，对提高GAN稳定性的策略和方法进行了研究，并进行了实验验证。

1 天文图像生成的GAN模型

1.1 原始GAN模型

GAN由两部分组成，分别是生成器(generator)和鉴别器(discriminator)。生成器是根据训练图像的像素概率密度分布将“初始随机噪声”不断地进行重构直到生成的图像像素概率密度分布无限趋近于训练图像的一种模型，其任务是使得生成的图像能够“以假乱真”。鉴别器的作用是区分生成图像和训练图像之间的差异，并在训练的过程中不断地加强自己的灵敏度。GAN模型可以由公式(1)来描述。

(1)

如图1所示,生成器将生成的图像与真实图像一同输入到鉴别器中,由鉴别器判断其真假。

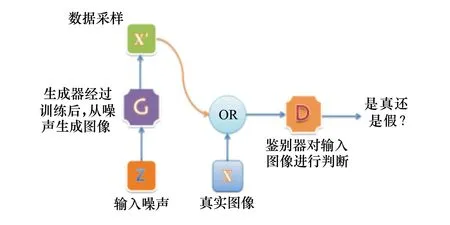
图1 GAN示意图

如图2所示,鉴别器同时从生成图像和真实数据中进行采样后进行对比,更新鉴别器参数。生成器从鉴别器中获得反馈,不断调整其参数使得生成图像的像素概率分布密度靠近训练图像。

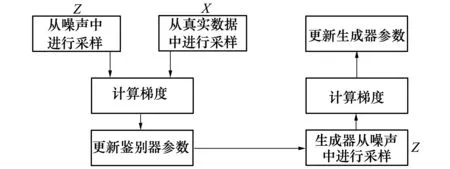
图2 生成器与鉴别器参数更新示意图

1.2 天文图像生成的GAN模型结构

本文使用Keras逐层搭建GAN模型,搭建过程示意图如图3所示。

图3 模型搭建示意图

本文所设计的图像生成模型与原始GAN模型相比进行了如下改进:①在生成器中的每个卷积层后都设置批归一化层,其目的是为了规范样本特征分布,提高神经网络学习速度；②在生成器的激活层采用 Relu而在鉴别器的激活层中均采用Leaky-Relu,其作用是在训练中避免模型崩塌；③取消所有池化层,在生成器中使用转置卷积(transposed convolutional layer)进行上采样,在鉴别器中使用微步幅卷积代替池化层。其作用是增强模型对图像细节的描述；④在随机抛弃层使用了全新的抛弃方法:S-Dropout,其作用是能够在保证模型稳定的前提下尽可能多地保留原始信息的传递。

1.3 模型的初始化

模型的初始化方式对生成图像的质量有着重要的影响。想要训练出一个性能出色的神经网络模型,通常会选择随机初始化而不是将所有参数初始化为0。这样做的原因是如果所有的神经元都具有相同权重的话,那么它们的激励结果也会相同,这样网络就无法通过神经元权重在反向传播时的更新来学习到不同的特征了。因此采用随机分布的初始化方式就能够保证每个神经元的初始权重不同,并且可以使模型学习到不同的、丰富的及有层次的特征。目前常用的权重初始化方法主要有2种,一种是平均分布,一种是高斯分布。本文选用平均分布来初始化模型,主要原因是在做内插值时,在曲线上做的效果比在直线上做的效果更好。另外,通过实验对比发现采用平均分布初始化生成的图像质量明显好于采用高斯分布初始化的结果。图4是采用平均分布初始化生成的图像。图5是采用高斯分布初始化生成的图像。显然,采用平均分布初始化的方式更能够在相对短的时间内学习到有用的信息。

图4 采用平均分布初始化的生成结果 图5 采用高斯分布初始化的生成结果

虽然GAN的提出极大丰富了图像生成的方法,但是它也有劣势,最主要的问题在于GAN较难训练。由于深度神经网络多层结构的特点,GAN通常具有大量的训练参数,而且训练参数的数量随着模型深度的加深呈几何级数增长。当训练图像的像素较高时模型通常会出现欠拟合或是过拟合的情况,这种情况被称之为训练不稳定。

2 天文图像生成的GAN训练策略

2.1 训练数据集

本文在基于GAN的天文图像生成研究中的所有训练数据来自于美国斯隆数字巡天数据库(sloan digital sky survey,SDSS),SDSS项目开始于2000年,以阿尔弗雷德·斯隆的名字命名,计划观测25%的天空,获取超过100万个天体的多色测光资料和光谱数据,目前该项目取得的观测结果涵盖了南银极周围7 500平方度的星空,记录到近200万个天体的数据,包括八十多万个星系和十多万个类星体的光谱数据,这些天体的位置和距离数据为人们研究宇宙的大尺度结构开辟了道路[24]。由于SDSS中原始图像的尺寸过大,无法直接进行训练,因此本文首先对原始的大尺寸星系与恒星图像按照随机分割的方式进行了分割,并得到了2类小尺寸的、适合训练的图像集,分别是10万张64×64×1大小的图像和30万张128×128×3大小的图像。天文图像通常具有5个颜色通道,分别是u,g,r,i,z[25]。其中64×64与128×128代表图像的长度和宽度,1(r通道)与3(g,r,i通道)代表图像的颜色通道数量。图6和图7分别给出了部分64×64×1训练图像和128×128×3训练图像。

图6 部分64×64×1训练图像

图7 部分128×128×3训练图像

2.2 稳定训练的策略

本文为了保持GAN模型在训练中的稳定,采用了多种方法。例如,批归一化层(batch normalization)被用在除最后一层的每个卷积层之后,这将保证有效梯度信息能够流过模型的每一层。

本文在生成器的每一个批归一化层的后面使用整流线型单元(Relu)作为激活函数。从信号的生物学角度上讲,Relu比被广泛使用的Sigmoid和tanh更加适合作为信号的激励函数。Relu可以被表示为f(x)=ln(1+ex),它与其他的激活函数相比,具有诸多优点:

1) Relu是一种稀疏激活函数,这意味着它将随机地对模型进行初始化，并且只有一半的隐层神经元会被激活,而其他将保持输出为0。

2) 它具有高效的梯度传播和计算效率且并不会像sigmoid一样容易出现梯度消失的问题。原因是当进行反向传播时,误差会从输出层逐层回传至顶层,并且会与每一层的输入神经元的值相乘。这个过程可以被表示为:fGradient=E·Sigmoid′(x)·x,相比之下,如果选择Sigmoid作为每层的激活函数的话,那么在回传的过程中,欠拟合就会很容易出现。这是因为误差会在逐层传播过程中呈指数级衰减,那么在经过多层回传后,梯度信息就会变得非常小从而降低模型的学习速率。Sigmoid激活函数可以被表示为S(x)=(1+e-x)-1。

因此,在生成器中本文采用Relu作为除最后一层外的每层的激活函数,而在鉴别器中使用Leaky-Relu。Leaky-Relu是Relu的一种变体,它能够允许节点在没有被激活的情况下获得一个很小的、不为0的梯度,如公式(2)所示。

(2)

“α”代表调参系数,通常情况下取值为0.2。

除此之外,本文在鉴别器中每个卷积层后使用随机抛弃方法(dropout);在生成器和鉴别器中同时使用Adam优化器[26];在生成器和鉴别器中使用不一样的学习速率,使得生成器的学习速率要略大于鉴别器;在生成器的最后一层使用tanh作为激活层;在鉴别器的所有层采用Leaky-Relu作为激活层。

3 GAN稳定性的增强

3.1 一种改进的随机抛弃方法(S-dropout)

为了防止在天文图像生成训练中出现过拟合,本文提出了一个改进的随机抛弃方法S-dropout。深度神经网络由于具有大量的神经元和权重参数,如果在训练中要同时更新所有神经元的权重,那么计算量将会非常巨大,而dropout的应用可以很好地解决这个问题,它可以在训练的过程中随机切断一部分神经元之间的连接,从而保证整个模型能够较为高效和平衡的进行训练。

原始dropout的工作方式是将每层所连接的神经元随机抛弃一半,然而固定的抛弃比例并非最优的选择,虽然按照50%的固定比例抛弃连接能够帮助模型保持稳定,然而这样也会损失一些有用的连接。因此本文提出将这个固定的抛弃比例改变成了衰减式抛弃。这样做的好处是,当训练图像的分辨率较高时,能够在保证模型稳定的前提下尽可能多地保留原始信息的传递,从而能够丰富生成图像的细节。本文将这种改进后的随机抛弃方法称为S-dropout。

(3)

如公式(3)所示,f(x)代表了当前随机抛弃的比例。x代表循环次数,k是调节参数且被设置为0.25,除了当x等于0的时候k等于0。

图8和图9分别是神经元全连接和使用S-dropout的示意图。

图8 使用全连接 图9 使用S-dropout

3.2 GAN中高级参数的优化

对抗模型中的高级参数取值是训练深度神经网络非常重要的一部分，然而当前的取值方法主要是靠经验来进行设置。例如，当训练图像分辨率较高时，应该使用较多的卷积层。这意味着使用较深层次的网络可以使模型尽可能多的学到训练图像中的细节。反之则使用较浅的模型，这样可以降低计算成本加快运算速度。本文首先由经验大致确定各个高级参数的取值范围，然后采用网格搜索法对这些重要参数的取值进行搜索尝试并对比其结果，最终确定了GAN高级参数的取值。表1是对模型所使用的优化器的网格搜索结果；表2是对循环次数及批处理大小的网格搜索结果；表3是对生成器和鉴别器最后一层激活函数的网格搜索结果。

表1 对优化器的网格搜索

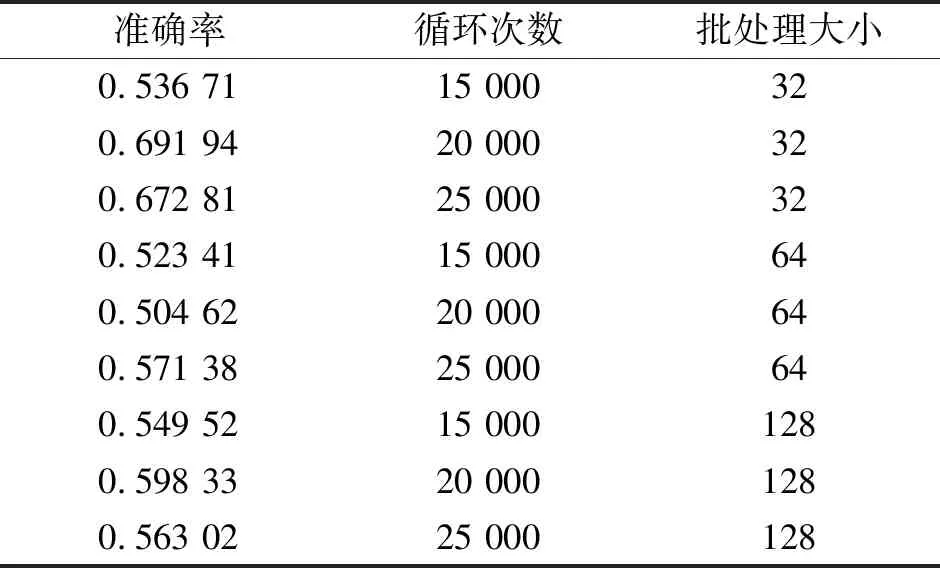
表2 对循环次数及批处理大小的网格搜索

表3 生成器和鉴别器最后一层激活函数的网格搜索

如表1～3所示,当模型的结构相同时,采用如下所述的高级参数组合能够生成更加清晰的,模型准确率最高的结果:在鉴别器,生成器及网络中均使用Adam作为优化器;选择循环次数20 000,且批处理大小为32;选取tanh和Leaky-Relu分别为生成器和鉴别器最后一层激活函数。

3.3 损失函数的改进

在对抗模型中,训练图像的像素概率密度分布与生成图像的像素概率密度分布的差异主要是靠“距离”来描述的。在原始GAN模型中,这个距离是由Jensen-Shannon散度[27](JS散度)来度量的。然而,GAN模型的不稳定与JS散度的特点有着很大的关系。JS散度可以被描述为由两部分KL散度[28]组成，(4)式和(5)式分别给出了KL散度和JS散度的表达式,其中,P1(x)与P2(x)分别代表2个数据分布。

GAN模型的训练过程其实是求损失函数最优解的过程。即求鉴别器损失函数最大值与生成器损失函数最小值的和的过程。鉴别器与生成器的损失函数分别如(6)式和(7)式所示。公式(8)是简化后的生成器的损失函数表达式,要求生成器损失函数的最小值等价于求公式(8)的最小值,也就是求训练数据与生成数据之间的JS散度最小值。

Dloss=-[Ex～pr[lgD(x)]-Ex～pg[lg(1-D(x))]

(6)

Gloss=Ex～pg[lg(1-D(x))]

(7)

Gloss=2JShannon(Pr||Pg)-2lg2

(8)

经过分析可知:当Pr(x)等于0且Pg(x)等于0时,或当Pr(x)不等于0且Pg(x)不等于0时,它们对于计算JS散度的贡献为0。其原因是当2个分布没有重叠或者重叠可以忽略时,它们之间的JS散度为0。而由于在GAN模型中,生成图像都是从低纬度(100维)的随机噪声生成的,然而生成的图像都是远远大于100维的高维图像,例如128×128的图像共有16 384维,那么这个时候随机噪声与生成图像之间就构成了一种从低纬度到极高纬度的映射,那么此时2个分布之间的重合部分可以被忽略;

当Pr(x)等于0且Pg(x)不等于0时,或Pr(x)不等于0且Pg(x)等于0时,生成器损失函数的最优解是一个固定值:lg2。这也就意味着有效的梯度信息无法在模型中进行传播,而且这种情况在生成图像分辨率越高时越严重。

文献[18]提出了wasserstein distance(EM-distance),EM-distance最大的优势在于能够有效描述2个没有共同部分的数据集差异。为了解决从低纬度的随机噪声生成高纬度图像过程中容易产生模型崩溃的问题,本文使用了EM-distance来替代原先的JS散度,形成改进的损失函数。

(9)式是EM-distance的表达式,(10)式是本文所采用的改进损失函数,(11)式是生成器的损失函数,(12)式是鉴别器的损失函数。

W(Pr,Pg)=infγ～Π(Pr,Pg)E(x,y)～γ[‖x-y‖]

(9)

floss=Ex～Pr[fω(x)]-Ex～Pg[fω(x)]

(10)

Gloss=-Ex～Pr[fω(x)]

(11)

Dloss=Ex～Pg[fω(x)]-Ex～Pr[fω(x)]

(12)

4 实验结果

为了验证基于GAN的天文图像生成方法的有效性,本文分别使用了10万张64×64×1和30万张128×128×3的训练图像对模型进行了训练,并将本文GAN的改进与采用原始对抗网络模型所生成的结果进行了对比。

图10 采用本文方法所生成的64×64×1图像 图11 采用原始对抗模型生成的64×64×1图像

图10和图11是采用64×64×1训练图像的生成结果。其中,图10是采用本文方法所生成的64×64×1的图像,图11为采用原始对抗模型生成的结果。图12是在训练中所使用的SDSS原图。由图10与图11相比较可知图10中生成图像的噪点要明显少于图11中的噪点,这表明本文方法更能够使模型保持稳定。

图13和图14是由64张128×128×3生成结果随机组合所构成的图像。其中,图13是采用本文方法所生成的图像的组合,图14为采用原始对抗模型所生成的图像组合。可以看出采用原始GAN方法生成的图像之间边界信息较为模糊,生成图像中的噪声较大;而本文方法生成的图像中噪声被有效抑制且生成的恒星和星系的细节更加细腻和清晰。

图12 SDSS原始图像 图13 采用本文方法生成的 图14 使用原始对抗模型生成的 128×128×3图像 128×128×3图像

表4 生成图像最终准确率

如表4所示，采用本文方法生成的64×64×1的图像(图10所示)的准确率为84%，采用原始GAN生成的图像(图11所示)的准确率为73%；采用本文方法生成的128×128×3的图像(图13所示)的准确率为97%，采用原始GAN生成的图像(图14所示)的准确率为86%。

5 结 论

本文将GAN用于生成星系与恒星图像，并针对GAN用于生成天文图像存在的问题，对GAN进行了改进。针对模型崩溃问题使用了多种稳定训练过程的方法并设计了合理的训练策略，取得了良好的训练效果；针对生成图像的细节不够细腻以及有效信息的传递效率不够高的问题，提出了一种改进的S-dropout；针对高级参数的取值优化问题，使用网格搜索法对模型中部分高级参数的取值进行了优化；针对原始GAN中采用的JS散度容易引发模型崩溃的问题，采用了EM-distance替换原模型中的JS散度。为了验证本文方法的有效性，分别使用了10万张64×64×1与30万张128×128×3对模型进行训练，结果表明采用本文方法生成的图像质量要好于采用原始对抗模型生成的结果，改进后的模型稳定性得到了提高。