空间目标的轨迹和姿态数据生成

陈尔康, 高长生, 荆武兴

(哈尔滨工业大学 航天学院, 黑龙江 哈尔滨 150001)

弹道导弹在空间中[1]会释放出包括弹头、诱饵、碎片在内的多种空间目标，这些目标形成了目标群。在攻防对抗系统仿真中不论是对目标群进行跟踪、识别还是拦截，都需要其较为精确的轨迹[2]和姿态数据，因此对空间目标的轨迹和姿态数据生成方法进行研究是非常必要的。

在大多数相关研究中，目标的轨迹数据一般根据椭圆弹道原理计算得到[3-4]。但这类方法忽略了地球扁率和自转的影响，生成的轨迹数据不够精确。与真实场景类似，目标的弹道由发射诸元确定，因此轨迹数据生成问题实际上是发射诸元的计算问题[5-6]。发射诸元的计算方法主要有弹道积分、对射表拟合、解析算法[7-8]和轨迹优化[9]等，但这些方法在计算诸元之前需要进行大量的计算作为准备。除此之外，目标群还还包括分导弹头和诱饵。这类目标在中段由母舱释放并作被动飞行[10]，因此只需计算出释放后的初始状态即可得到轨迹数据。诱饵的初始状态可根据其具体类型设定释放相对速度矢量后计算得到。而分导弹头的初始状态则需满足命中指定目标点的要求，需按照一定的分导策略进行计算[11]。文献[12]对若干种不同分导策略进行了研究并得出了最优分导策略。文献[13]则应用极小值原理推导了分导速度增量的近似解析解，但无法得到能够精确命中设定目标的轨迹数据。随着诱饵技术的不断发展，单纯的轨迹信息难以识别出真弹头，必须考虑目标运动细节信息[14]。文献[15-16]将目标除质心平动以外的微小运动定义为微动并分析了其特点，建立了振动、旋转、翻滚和锥旋四类典型微动的模型，并发展成为中段目标识别的重要手段[17]。但相关研究只关注雷达信号的结果，缺少对目标姿态数据生成方法的研究。本文从目标数据生成的角度出发，根据弹道导弹的动力学特性和飞行程序设计了4种类型的基准弹道并给出了对应的诸元计算方法。并在此基础之上，提出了一种分导弹头最优速度增量的实时计算方法。最后针对目标的微动特性，设计了姿态数据的快速生成算法。

1 数学模型

1.1 质心运动模型

考虑地球扁率和自转，在发射系内建立弹道导弹质心的运动模型[18]如下

(1)

式中,ρ为导弹相对发射系的位置;v为导弹相对发射系的速度;P为推力;R为气动力;g为引力加速度;ae为牵连加速度;ak为哥氏加速度。

气动力在速度坐标系中分解为如下形式

(2)

引力加速度沿地心矢径r方向和地球自转角速度ωe矢量方向分解如下

g=grr+gωeωe

(3)

式中，gr和gωe的表达式分别为

(4)

式中，μ为地球的引力常数;r为地心距;ae为地球赤道平均半径;J2为带谐系数;φ为地心纬度。

1.2 主动段飞行程序

弹道导弹的轨迹主要由其主动段决定,由于弹道导弹的轨迹近似位于射面以内,因此其飞行程序主要由其俯仰角变化规律决定。工程上将其主动段飞行程序分为3段[18]:

第1段为垂直上升段,导弹俯仰角保持90°不变。第2段为转弯段,该段内攻角变化规律如下:

(5)

式中，αm为攻角绝对值的最大值,称为限制攻角。

第3段为瞄准段，此段中攻角保持固定值αx不变,称为瞄准角。

2 基准弹道设计

2.1 弹道类型分析

在没有瞄准段能量管理,即瞄准角为零的情况下,导弹的射程随限制攻角的增大呈现先增大后减小的变化趋势。因此某个中间射程会对应2个限制攻角值,但这两个值所对应的弹道高度是不一样的,一高一低,分别对应高弹道和低弹道。

而在瞄准角不为零时,弹道高度下压,起到了调整弹道高度的作用,称为固定高度弹道。此外,同一个射程对应着多个限制攻角和瞄准角的组合,其中存在导弹关机点机械能最小的组合,该组合对应的弹道即为最小能量弹道。

2.2 发射诸元计算方法

考虑到弹道导弹主要在射面内飞行且其射程随限制攻角先增大后减小的特点,采用大步长遍历粗搜索与精确迭代相结合的方法计算发射诸元,如图1所示。首先通过球面三角算出发射方位角的粗搜索值,然后进行限制攻角和发射方位角的遍历,最后通过精确迭代计算出发射诸元。

图1 发射诸元计算流程

3 分导弹道设计

3.1 理论分析

为便于分析和仿真计算,本文采用脉冲变轨的方式并忽略再入段。这样分导弹道的设计就简化为经典Lambert问题[19]。

由分导点扫过地心角θ至目标点的时间ΔT可由拉格朗日转移时间方程表示[20]

(6)

式中,μ为引力常数;a为轨道半长轴;α和β为拉格朗日参数,cosα=1-s/a,cosβ=1-(s-c)/a,s=(rk+rb+c)/2,c为分导点与目标点之间的距离。

因此飞行时间ΔT与半长轴a之间的关系如图2所示。

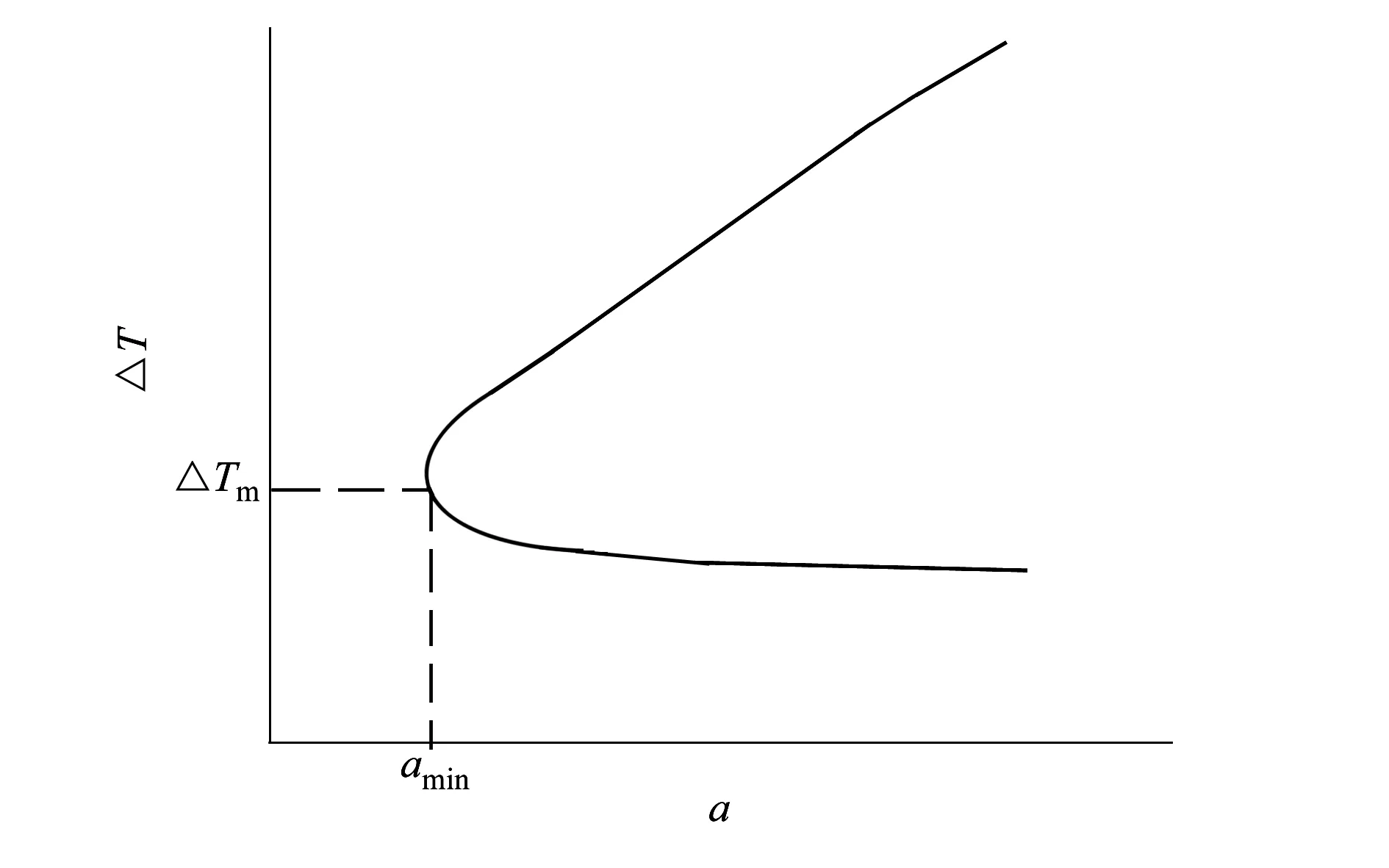
图2 ΔT与a的关系

在ΔT<ΔTm时,ΔT随a增大而单调递减;在ΔT>ΔTm时,ΔT随a增大而单调递增。

而轨道偏心率为[19]

(7)

记分导点处基准弹道的速度为vc1,分导弹道的速度为v1,则机动速度增量为

(8)

式中

因此增速ΔV与半长轴a之间的关系如图3所示。

图3 ΔV与a的关系

由图2和图3可知:在ΔT<ΔTm时,ΔV随a增大先减小后增大;在ΔT>ΔTm时,ΔV随a增大而单调递增。因此存在飞行时间ΔTvmin使得增速ΔV最小

ΔV(ΔTvmin)=minΔV(ΔT)

(9)

3.2 增速计算方法

根据3.1节的分析结果,本文设计了一种搜索最小增速的双层迭代策略。

对某一固定飞行时间,构造如下指标函数

J(X)=(GT(X)TG(X)

(10)

式中,G(X)为残差,取为

G(ΔVx,ΔVy,ΔVz)=[rbx-rfx,rby-rfy,rbz-rfz]T

(11)

式中，[rbx,rby,rbz]T为b点的地心矢径,[rfx,rfy,rfz]T为分导弹头由分导点K飞行ΔT时间后的地心矢径。

采用如下迭代格式使(12)式中指标最小

Xk+1=Xk-A-1B

(12)

式中

(13)

经过迭代后可得增速为

(14)

对于外层迭代,在增速最小时有

ΔV′(ΔT)=0

(15)

运用牛顿迭代法有迭代公式

(16)

如此反复迭代即可计算得到最小增速ΔVmin及其对应的飞行时间ΔTvmin。

4 微动姿态数据生成

4.1 理论分析

由于中段目标一般为自旋稳定,因此其微动特征主要是其受干扰力矩作用产生的进动。在释放过程中,中段目标会受到冲量Q的作用[21],可将其按横向和纵向分解为

(17)

式中,η为冲量Q与目标对称轴的夹角。

进动周期和进动角为

(18)

式中,It为目标横向转动惯量,Is为目标纵向转动惯量。

由(17)式和(18)式可知,虽然进动特性涉及参数很多,但主要特征为进动周期和进动角。因此数据生成算法应根据这2个量生成目标的姿态数据。

4.2 姿态数据计算方法

在仿真中目标姿态一般以相对于地球固联坐标系姿态角的形式给出,具体如图4所示。其中o-XEYEZE为地球固联坐标系,o-x1y1z1为目标的弹体坐标系,ψe为偏航角,φe为俯仰角。而滚转角γe为oz1轴与ox1轴、oZE轴所确定平面的夹角。由于本文考虑的目标均做自旋运动,因此根据自旋角速度计算滚转角即可。

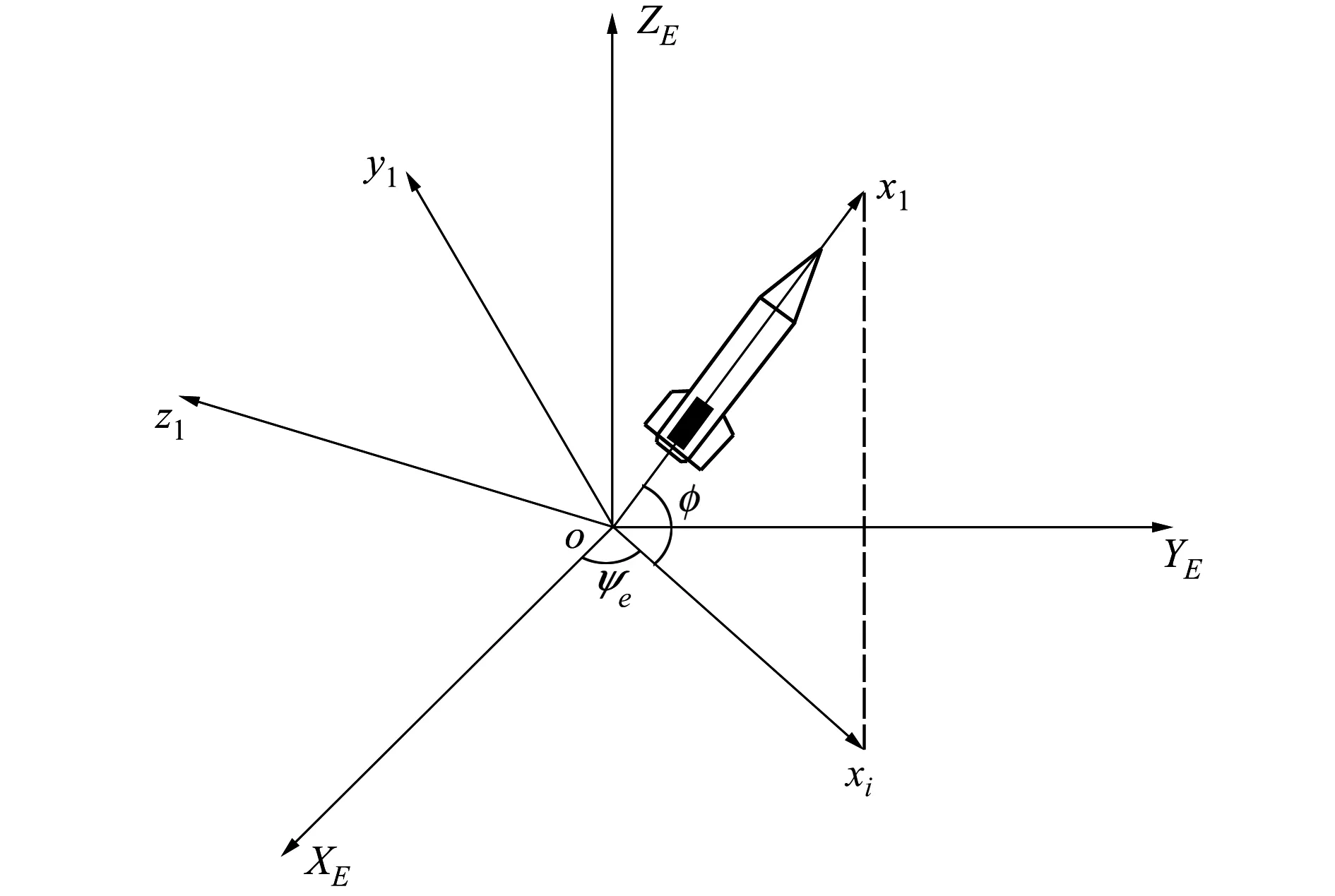
图4 姿态示意图

记沿ox1、oy1轴的单位向量为i,j,经坐标转换后在地固系的坐标分别为[ixe,iye,ize]T、[jxe,jye,jze]T。

则俯仰角、偏航角为

(19)

为便于计算建立角动量惯性坐标系,以角动量方向(即进动轴方向)为X轴,任意选择与X轴构成右手坐标系的Y轴和Z轴。与体系间的姿态角分别为进动角θ、章动角ψ和自转角φ。体系到角动量惯性系的坐标变换矩阵为

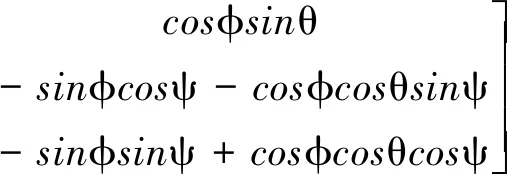
(20)

角动量惯性系到释放瞬时弹体系的坐标转换矩阵为

(21)

释放瞬时弹体系到地固系的转换阵为

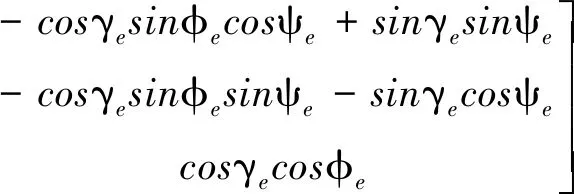
(22)

释放瞬时地固系到地固系的转换关系只与自转角λ=ωeΔT有关

(23)

由以上坐标变化关系可计算弹体系到地固系的坐标转换矩阵

Ce1=CefCfaCapCp1

(24)

至此已求出了i,j在地固系中的坐标,代入(19)式即可计算出姿态角。

5 仿真分析

5.1 基准弹道设计

对基准弹道设计方法进行仿真验证,以某导弹为仿真对象,发射点设为(155.462°W,19.653°N),目标点设为(116.395°E,39.922°N),初步计算目标射程为8 481.88 km。本文提出方法(方法1)的弹道设计结果分别如表1和图5所示。为便于比较,文献[8]中方法(方法2)的弹道设计结果如表2所示。

表1 基准弹道设计结果(方法1)

表2 基准弹道设计结果(方法2)

图5 基准弹道

由表1和表2可知，2种方法计算出的诸元非常相近，说明本文提出的方法能够给出足够准确的弹道数据。而在计算时间上，虽然方法2的迭代时间小于方法1的总耗时，但方法2事先需要大量时间计算弹道进行拟合，在处理不同的多个发射点时计算耗时会进一步增大，因此方法1在应用灵活性和计算耗时上优于方法2。由图5，4种类型的弹道均以较高的精度命中目标点，且由于弹道类型不同其弹道高度也不同，其中固定高度弹道和最小能量弹道的弹道高度位于高弹道和低弹道之间。

5.2 分导弹道设计

以5.1节中的高弹道为基准弹道进行分导弹道设计的仿真。设置分导时刻为发射后350 s，分导目标点为(117.216°E,39.128°N)，设计结果如图6所示。其中横程偏差为0.8 m，纵程偏差为8.36 m，计算耗时为0.894 s。利用最优分导方法计算分导弹道，其横程偏差为35.4 m，纵程偏差为247.6 m，计算耗时为0.115 s。虽然该方法计算耗时更短，但由于该方法未使用精确模型迭代计算，因此精度不如本文提出的方法，难以用于系统仿真中。

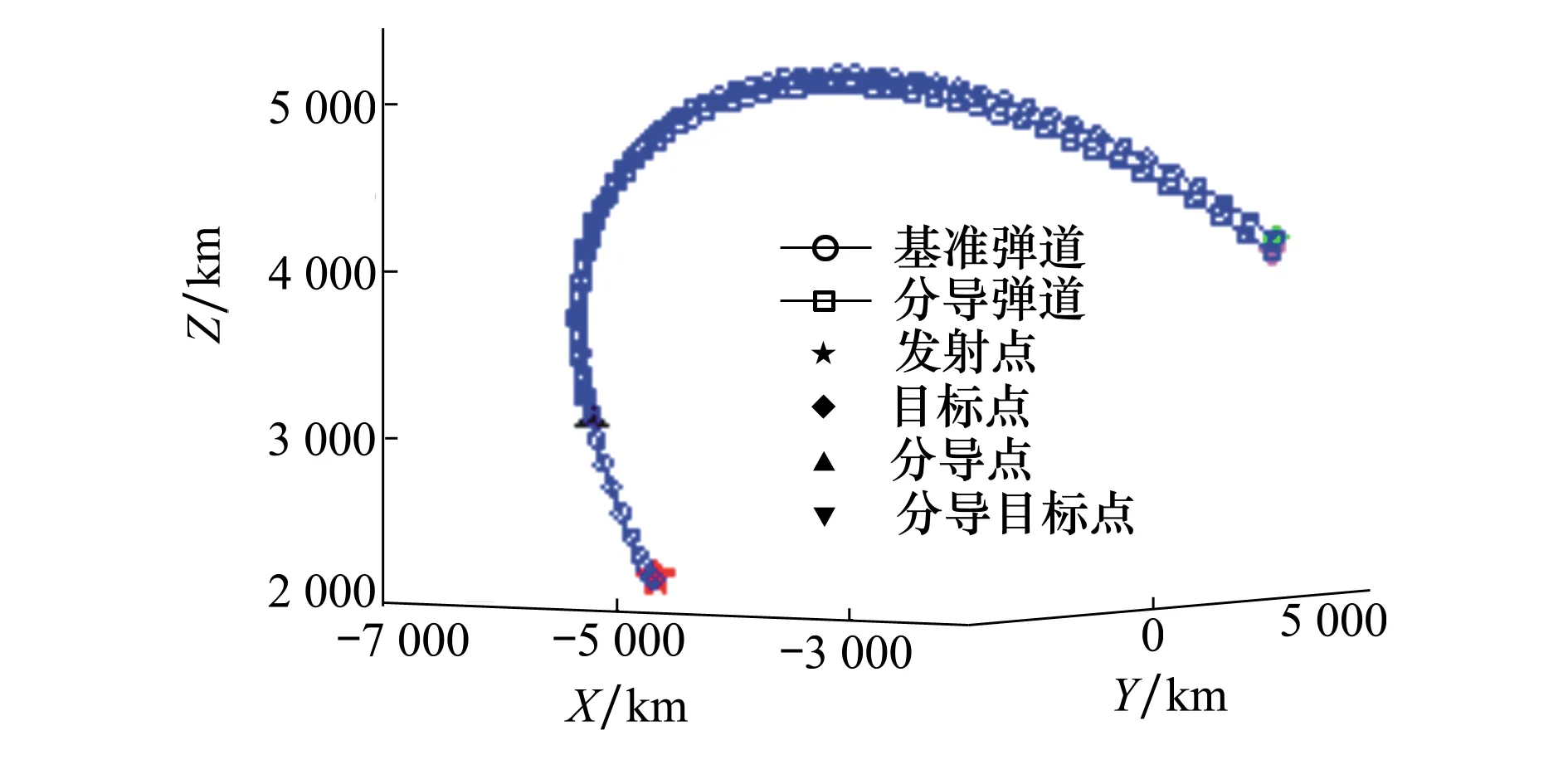
图6 分导弹道

可以看到分导弹道以较小偏差命中分导目标点，且计算耗时较少，能够满足仿真需求。

5.3 姿态数据生成

同样以5.1节中的高弹道为基准弹道进行诱饵姿态数据生成的仿真。设置进动角为4°，自旋周期为0.1 s，锥旋周期为0.5 s，释放时间为发射后400 s。分别使用本文方法(方法1)和传统的姿态动力学方程积分方法(方法2)计算姿态数据，仿真结果如图7和图8所示。

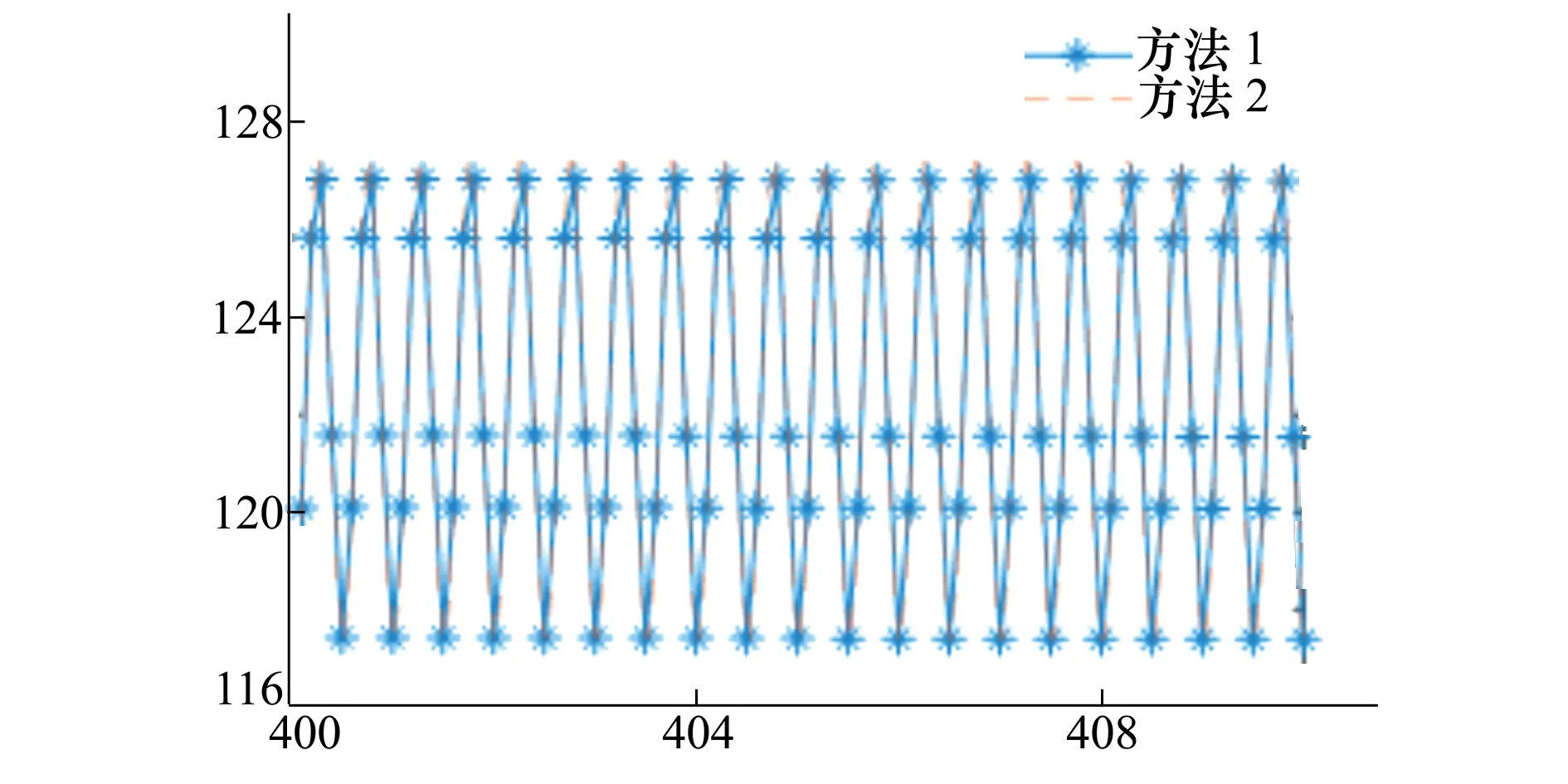
图7 偏航角

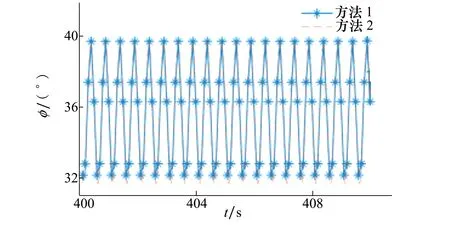
图8 俯仰角

可以看到本文提出的方法与直接积分动力学方程的计算结果一致，但本文方法无需进行积分计算，在计算时间上有优势，适于系统仿真使用。

6 结 论

以系统仿真中的目标数据生成为研究对象，考虑仿真的特点，对各类目标的特性进行分析并建立了相应的模型，给出仿真数据的生成方法：

1)根据导弹飞行程序特点和弹道特性将基准弹道分为4类，并设计了相应的弹道诸元计算方法。该方法将诸元计算分为粗搜索和精搜索两部分，无需事先准备工作即可快速准确地生成基准弹道数据。仿真结果表明，该方法能够生成准确的轨迹数据；虽然总计算耗时大于传统方法，但传统方法在迭代前的准备工作需要耗费大量时间，而本文提出的方法并不需要任何准备工作，因此该方法能够更好地满足系统仿真的要求。

2)将分导弹道的设计问题转化为Lambert问题，分析了飞行时间与分导增速的关系。基于此关系，提出了一种最小增速分导弹道规划方法。这一两层迭代算法能够计算处分导弹头的最小增速。利用这一增速即可计算出分导弹头的弹道数据。与传统方法相比，该方法虽然计算耗时小幅增加，但精度明显提高，更适合系统仿真使用。

3)分析了中段目标的姿态微动特性，设计了一种通过坐标转换矩阵计算姿态数据的方法，能够快速准确的生成包含目标微动特性的姿态运动数据。仿真结果表明，该方法计算得到的姿态数据与动力学模型积分计算的结果一致，能够准确反映目标微动特性，且计算耗时短，使用方便，符合仿真的要求。