基于改进Kriging模型的舰载机着舰下沉速度影响性分析研究

薛小锋, 王远卓, 路成

(1.西北工业大学 航空学院, 陕西 西安 710072; 2.西北工业大学 航天学院, 陕西 西安 710072)

下沉速度是舰载机在航母上着舰时飞机速度在竖直方向的分量，用于度量舰载机着舰撞击能量，是影响舰载机起落架性能和载荷的主要参数，其量值直接影响起落架及机体结构的重量[1]。因此舰载机着舰下沉速度的确定至关重要，偏小可能导致结构太弱，不能保障安全性要求；偏大则可能导致结构重量及安全余度过大，影响飞行性能。

舰载机着舰过程原理复杂，其理论模型涉及到飞行动力学、飞机操控、结构强度设计等多个学科[2]，舰载机下沉速度受到飞行姿态、飞机类型、着舰时机(白天/夜晚)、航母姿态及海况等多方面因素影响，而这些参数之间也存在相互影响，难以直接通过理论推导建立下沉速度与影响参数之间的分析模型。关于飞机着舰或着陆下沉速度的研究，国外已有一系列相关标准和指南[3-4]，美军标MIL-A-8863C给出了下沉速度、进场速度等着舰参数的统计规律，包括分布形式及均值、标准差；另有美国海军报告[5]提供了预警机、战斗机等各类舰载机在不同工况下的着舰下沉速度实测数据；文献[6-10]进行了舰载机着舰过程的运动学和动力学理论计算及仿真分析，主要包括与下沉速度有关的发动机响应、舵面效率等参数的变化机理[6]，下沉速度偏差的修正仿真[7]，考虑下沉速度的舰载机着舰动力学模型[8]和拦阻钩主动撞击过程[9]，与飞行员行为有关的下沉速度规律[10]。国内对舰载机着舰下沉速度研究的报道较少，主要是对美军标中关于着陆或着舰下沉速度要求的概述[11-12]、参考美军标进行着舰下沉速度计算[13]，根据舰载机着舰时的运动学关系和动力学关系推导着舰参数的理论公式[14]，以及舰载机拦阻着舰动力学分析与仿真[15-16]，舰载机起落架性能设计[17-18]，海况导致的航母姿态对舰载机着舰的影响分析[19-20]等。但实际舰载机下沉速度综合受到飞机姿态、海况、航母运动等方面参数的共同影响，由于分析涉及参数较多，维度较高，对于下沉速度预测问题，传统Kriging模型在求解超参数θ过程中容易陷入局部最优，进而导致所建立的模型预测结果与实测值存在较大误差[21]。因此，需要找寻适用的方法建立各种影响因素与下沉速度之间的数学模型，进行各因素的影响程度研究，确定型号飞机的下沉速度。

由于我国舰载机研制较晚，国内未见有舰载机着舰实测数据的公开报道。因此，本文拟借鉴国外现役舰载机F/A-18A的着舰姿态统计数据，首先通过多元统计分析中的偏相关分析方法，确定出下沉速度的关键相关参数，这些变量主要包括进场速度、舰上结合速度、飞机瞬时下滑角及甲板俯仰角等参数；接着运用Kriging插值代理模型和遗传优化算法，建立下沉速度与上述关键相关参数之间的改进Kriging代理模型，进而进行各参数对下沉速度的影响程度分析，发展出一套基于实测数据的适用于舰载机下沉速度影响性分析方法，为舰载机的研制提供基础性技术支持。

1 基于改进Kriging模型的参数影响性分析方法

本文借助Kriging模型良好的数据插值特性，拟对舰载机下沉速度影响因素及其规律进行探讨。

1.1 插值模型构建

1) 插值形式

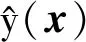
(1)

式中：fT·β为多项式回归模型,f=[f1(x),f2(x),…,fp(x)]T为x的回归基函数,在Kriging模型中取为x的多项式;β为各回归基函数的待定系数;p为回归基函数的个数,与所选择的回归基函数形式和自变量个数有关;z(x)为关于样本的一个随机过程,根据样本进行模型误差修正。因此,Kriging模型即为样本的确定性回归部分fT·β与局部偏差的近似z(x)之和。

2) 误差修正部分

Kriging模型的误差修正部分z(x)可用一个均值为0,方差为σ2的随机过程表示,其统计特性如下:

E[z(x)]=0

var[z(x)]=σ2

cov(z(xi),z(xj))=σ2R(θ,xi,xj)

(2)

式中，R(θ,xi,xj)为任意2组样本xi,xj之间的相关函数

(n为变量个数)

(3)

常用的相关函数有高斯型、指数型、线性型及立方型等形式,其中高斯型相关函数有着良好的计算精度,基于高斯型的相关函数可表示如下[21]

(4)

式中,θ为相关函数的修正系数；xi,k,xj,k分别为样本xi,xj的n维分量中的第k维分量。因此,对于m个样本而言,相关函数矩阵表示如下

R=

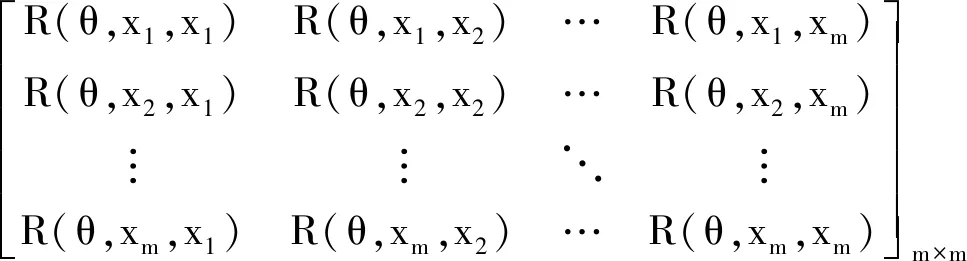
(5)

3) 多项式回归部分

目前,Kriging模型常用的回归基函数有常数形式、一次形式和二次形式3种,具体来讲:

(1) 常数形式,p=1;

f1(x)=1

(6)

(2) 一次形式,p=n+1;

f1(x)=1,f2(x)=x1,…,fn+1(x)=xn

(7)

(8)

对于m个样本,Y=[Y1,Y2,…,Ym]T,x=[x1,x2,…,xm]T,则有回归基函数矩阵如下所示

(9)

进一步可得到各回归基函数的待定系数向量:

β=(fTR-1f)-1fTR-1Y

(10)

4) 误差评估

综上,对于任意点x,上述Kriging模型给出的预测结果中的局部偏差为

z(x)=rT(x)R-1(Y-fβ)

(11)

式中,r(x)=[R(θ,x,x1),R(θ,x,x2),…,R(θ,x,xm)]T表示任意点x与已知样本之间的相关程度。

根据最小二乘估计原理,Kriging模型预测结果的方差估计值σ2可表示为

(12)

1.2 基于遗传算法的相关函数修正系数优化

通过前述推导可以看出,Kriging模型的回归基函数的待定系数、方差估计均和相关函数的修正系数θ有关,因此,需根据样本确定合适的θ值,才能使得Kriging模型精度最高。修正系数θ的优化求解模型如下:

(13)

式中,目标函数值是以适应度函数最小为优化目标,目的是保证在参数寻优过程中保证预测值与实测值的误差尽可能小,进而保证所建立的模型预测精度满足工程需求。

修正系数θ的目标函数φ(θ)存在局部最优的可能,考虑到遗传算法有着较好的全局寻优能力,本文根据下沉速度样本数据,采用遗传算法对Kriging模型的相关函数的修正系数θ进行寻优。具体流程如图1所示。

由图1可知,基于遗传算法的Kriging超参数求解具体流程如下:依据获取的数据,选取相关变量的样本数据并对数据进行归一化处理;定义求解过程中的优化变量即超参数θ,对变量进行编码初始化种群;依据适应度函数计算适应度值,选取种群中的最优个体;通过交叉操作生成下一代个体形成种群,进而进行变异操作,计算目标函数值;判断目标函数值是否满足终止条件,如果不满足条件,则需重新执行适应度值计算,如果满足条件,则输出优化参数值。

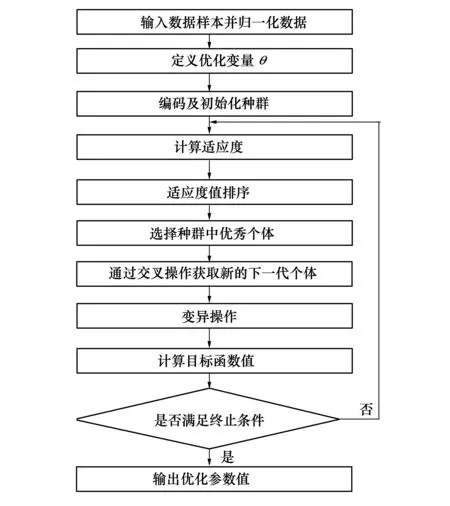
图1 基于遗传算法的相关系数优化过程

2 F/A-18A着舰下沉速度的相关参数确定分析

2.1 F/A-18A飞机着舰状态参数

按照JSSG-2006中的描述,F/A-18A舰载机着舰参数包括如下3类,共16个[5]:

1) 飞机姿态参数

进场速度、舰上接合速度、下沉速度、飞机着舰重量、飞机瞬时下滑角、飞机俯仰角、飞机滚转角、飞机偏航角、飞机滚转率、飞机俯仰率、飞机航迹角等。

2) 着舰操作参数

拦阻偏心距、舰尾到着舰点距离。

3) 着舰环境参数

甲板俯仰角、甲板侧倾角、舰船速度。

2.2 下沉速度相关参数确定

文献[5]中提供了F/A-18A舰载机的252个有效着舰参数样本,结合多元统计分析中的偏相关分析原理和方法[2],将各着舰状态参数(不包括下沉速度,共15个)与下沉速度的偏相关系数计算结果列入表1。

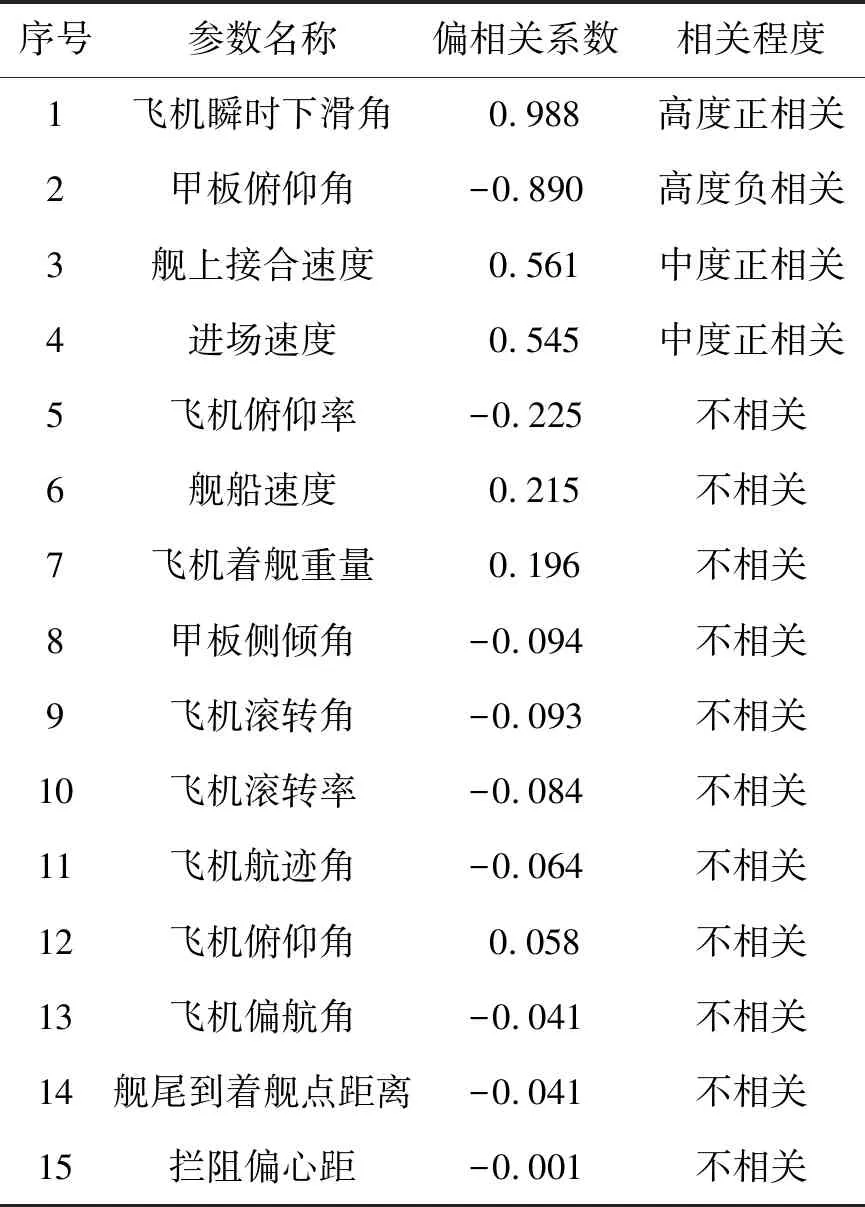
表1 F/A-18A着舰参数与下沉速度相关性分析结果

由相关性分析结果可知,飞机瞬时下滑角、甲板俯仰角与下沉速度高度相关,进场速度、舰上接合速度与下沉速度中度相关。飞机俯仰率、舰船速度、飞机着舰重量、甲板侧倾角、飞机滚转角、飞机滚转率、飞机航迹角、飞机俯仰角、飞机偏航角、舰尾到着舰点距离、拦阻偏心距与下沉速度不相关。从而可确定F/A-18A舰载机下沉速度VS的相关参数包括:飞机瞬时下滑角CG、甲板俯仰角CP、进场速度VA及舰上接合速度VE等4个参数。进一步建立这4个参数与下沉速度的改进Kriging插值模型,并进行各参数影响程度分析。

3 F/A-18A舰载机下沉速度的改进Kriging模型及分析

3.1 下沉速度的改进Kriging模型

F/A-18A舰载机的252个着舰状态样本各参数的均值和标准差如表2所示。本文选择其中的126个样本进行改进的Kriging插值模型构建,采用另外126个样本进行模型的检验。

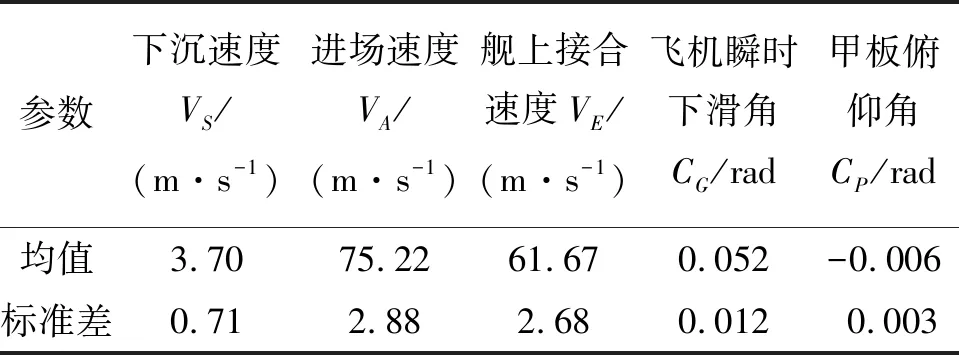
表2 F/A-18A着舰参数均值及标准差

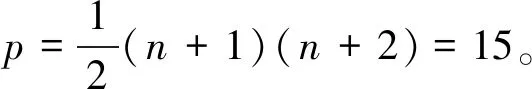
目标函数寻优过程如下:

采用拉格朗日乘子法进行求解,目标函数最终收敛到0.065 692,收敛过程如图2所示;

图2 θ的目标函数收敛过程-拉格朗日乘子法

进一步采用遗传算法进行优化求解,目标函数的进化过程如图3所示,经过100代优化迭代该目标函数收敛。最优值0.060 538,优化结果为:θ=[363.683 0.008 493.786 327.062]T。可以看出,由于目标函数具有局部最优的特性,拉格朗日乘子法计算到18步停止计算,并未收敛到最优值;而遗传算法通过进化迭代最终得到了最优结果。进一步可计算得到R和β,具体如下:

R=

图3 θ的目标函数进化过程-遗传算法

3.2 误差评估及与其它模型对比

针对前述得到的下沉速度改进Kriging模型与其他方法进行对比,对比方法包括下沉速度预测经验公式[2]、普通Kriging模型以及本文的改进Kriging模型,将文献[5]中另外的126个样本的进场速度VA、舰上接合速度VE、飞机瞬时下滑角CG及甲板俯仰角CP分别代入以上模型中。下沉速度实测值及各种模型的预测结果对比如图4所示,误差对比如图5及表3所示。

图4 不同方法的下沉速度预测结果与实测值对比

图5 不同方法的下沉速度预测结果误差对比

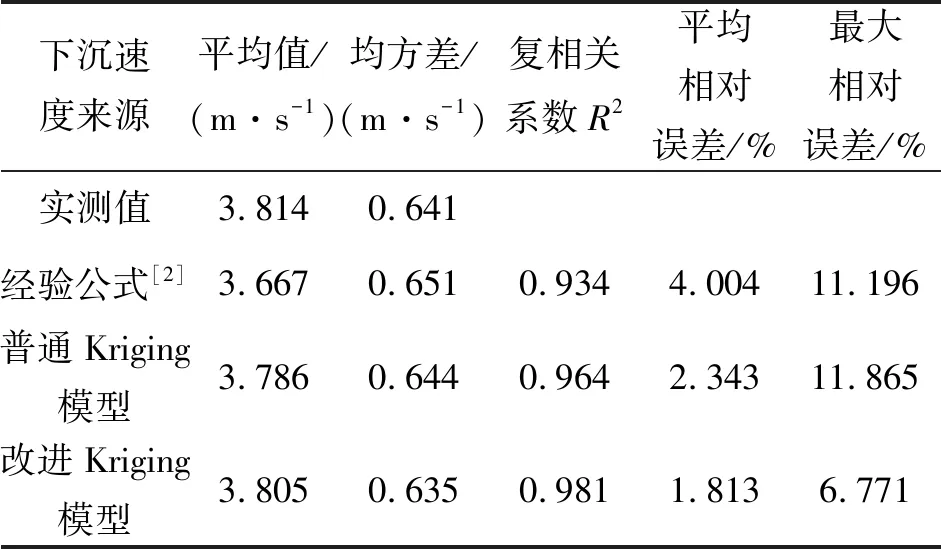
下沉速度来源平均值/(m·s-1)均方差/(m·s-1)复相关系数R2平均相对误差/%最大相对误差/%实测值3.8140.641经验公式[2]3.6670.6510.9344.00411.196普通Kriging模型3.7860.6440.9642.34311.865改进Kriging模型3.8050.6350.9811.8136.771

表3中对比结果显示，相比下沉速度经验公式及普通Kriging模型，改进的Kriging模型给出的下沉速度预测结果的复相关系数(复相关系数越接近1表示精度越高)、平均相对误差及最大相对误差等精度指标是最好的。因此，可通过改进的Kriging模型得出不同进场速度、舰上接合速度、飞机下滑角以及甲板俯仰角下的着舰下沉速度并进行预测。舰载机着舰参数对下沉速度有着很大影响，按照飞机总体设计和飞行力学相关理论进行下沉速度正向推导太过复杂，甚至难以实施。基于实测数据，通过偏相关分析及本文的下沉速度改进Kriging模型，进行逆向拟合推导，可初步得到下沉速度与各着舰参数之间的内在联系，即下沉速度是进场速度或舰面结合速度的竖向分量，同时在着舰过程中又与飞机瞬时下滑角及甲板俯仰角有关，并通过Kriging模型的随机误差补偿作用，相比经验公式，本文模型预测值与实测值更加吻合。

4 结 论

舰载机着舰下沉速度受航母、海况以及飞机飞行姿态的影响。本文基于F/A-18A飞机的着舰实测数据，采用多元统计理论的偏相关分析方法和改进的Kriging插值代理模型，探索了实际使用环境下各着舰参数对舰载机着舰下沉速度的影响，形成如下结论：

1)由F/A-18A飞机的着舰实测数据相关分析可知，飞机瞬时下滑角、甲板俯仰角、进场速度及舰上接合速度等4个参数与下沉速度的相关程度较强，可用于建立下沉速度的影响性分析模型；

2)将遗传算法用于Kriging模型相关函数待定系数的优化求解，形成了改进的Kriging插值代理模型，提高了模型插值精度；

3)将F/A-18A飞机的252个着舰实测数据样本分为2组，其中一组的126个样本用于建立下沉速度的改进Kriging模型，另外一组的126个样本用于模型验证，与经验公式及普通Kriging模型对比，本文模型给出的下沉速度预测结果的精度指标均为最好，可用于舰载机下沉速度预测及影响因素分析研究。