双材料界面裂纹动态应力强度因子有限元分析

马振洲，王小乐，刘恩欣，杨文坡

(1.河北渤海投资集团有限公司， 河北 沧州 061113； 2.黄骅市常郭镇政府， 河北 沧州 061112)

双材料界面普遍存在于大量工程结构和材料之中，如岩基与混凝土坝的交界面，复合材料的结合面等。由于界面本身通常比构成界面的材料性能要差，因此总是比较容易在结合面附近产生裂缝，并沿界面发生扩展直至结构破坏[1]。在实际工程中，可能会遇到含有裂纹的结构体受到动态载荷作用的情况[2]。为了保证结构在工作时的安全性，需要对裂纹体在动载荷作用下的响应进行分析。而动态应力强度因子是反映裂缝尖端应力和位移等重要力学性质的参数，不少学者就带裂纹的材料进行了动态应力强度因子的计算和试验研究[3-9]，但这些研究都是在均质材料下进行的，而对界面结构动态响应分析却鲜有涉及。考虑到工程实际中多存在界面问题，本文利用双材料界面力学理论对四点剪切复合试样在冲击荷载作用下的动态应力强度因子进行计算分析，并通过均质的三点弯曲试样在冲击荷载下的动态响应分析验证该理论的有效性，进而为解决界面结构动力问题提供参考。

1 双材料界面理论

考虑由两种不同材料组成的无限大平面，在交界处有一半限长裂纹，如图1所示。其中，y>0的区域为材料1，y<0的区域为材料2。各材料对应的弹性模量、剪切模量和泊松比分别为E1、μ1、ν1和E2、μ2、ν2。

图1双材料界面裂纹模型

在数值计算中，对界面裂纹问题的分析常采用直角坐标系，开口位移(裂缝剪切位移和张开口位移分别记为δx和δy)定义如下：

δx=ux1(r,π)-ux2(r,-π)

δy=vy1(r,π)-vy2(r,-π)

(1)

裂纹面开口位移表达式[1]为：

(2)

(3)

式(1)中：u和v分别为裂缝翼缘x方向和y方向的位移值；r为裂缝翼缘到裂缝尖端的距离。式(2)中，ε为界面裂纹的振荡因子，定义见式(3)，其中，β为Dundurs参数中的值，结果见表1；κ为材料的卡帕参数；L为特征长度，即裂纹长度的倍数；K1、K2分别称为界面张开型和剪切型应力强度因子，按照该公式的定义，虽然二者与均质材料裂纹所对应的应力场不同，但它们的量纲却与均质材料裂纹应力强度因子完全一致。通过进一步推导，可得K1、K2的表达式[10]见式(4)和式(5)：

(4)

(5)

其中，E*为式(6)的简化形式，

(6)

动态断裂问题比静态问题要复杂，它不仅要考虑惯性效应，而且还要考虑应力波在结构内的传播。对于有预制裂纹的结构体在冲击载荷作用下的动力响应须满足式(7)运动平衡方程：

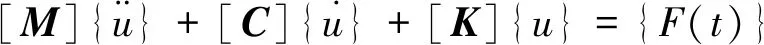
(7)

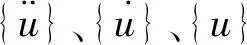
2 模型分析

2.1 界面模型分析

算例对由岩石和混凝土两种材料组成的四点剪切复合模型进行动力响应分析。其中，两种母材的力学参数见表1。复合模型尺寸大小见图2。冲击荷载为线性冲击荷载和正弦冲击荷载两种形式，如图3所示，荷载作用时间为80 μs，通过调整两种材料的相对长度，计算100 μs内不同模态下的动态应力强度因子。

表1 材料力学参数

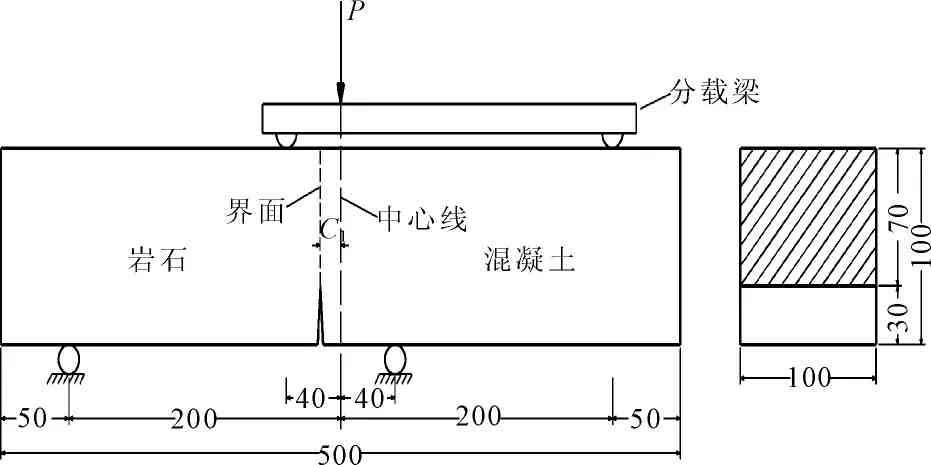
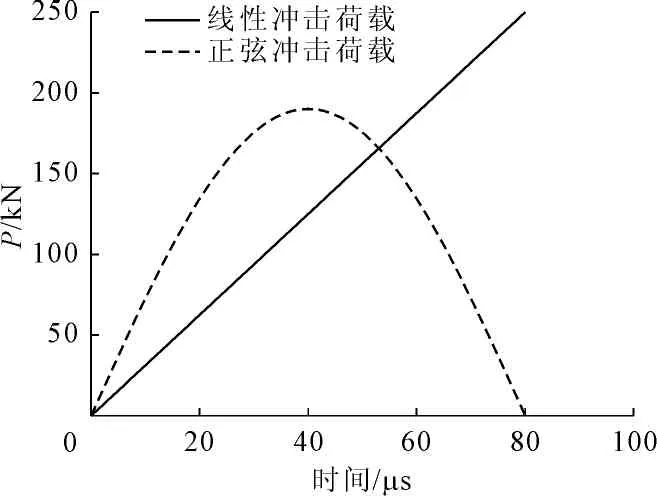
图2 四点剪切试样复合模型(单位：mm)

图3冲击荷载形式

界面力学中将复合模态角ψ定义如下：

ψ=arctan(K2/K1)

(8)

为了使模态角较为均布，通过试算最终选取以下三种情况进行分析。四点剪切复合模型的基本参数如表2所示。

表2 四点剪切复合模型基本参数

本文采用ANSYS软件的中Plane 183单元(Plane 183单元为二维八节点平面奇异单元，利用前处理KSCON命令，可以设置裂缝尖端的奇异性[13]，可用来解决二维断裂问题)对岩石/混凝土四点剪切复合梁进行建模，按照平面应力假定，计算界面动态应力强度因子(计算时取L为2倍裂纹长度)。为了模拟裂缝尖端应力、位移的r1/2奇异性，需要对裂纹尖端网格进行细分，并将裂缝尖端周围的等参单元各条边中的节点移至靠界面裂缝尖端的1/4分点处[14]。

采用双材料界面理论对四点剪切复合模型进行动态响应分析时，只需将对应的材料力学参数输入到软件中，由于母材性质的差异以及模型受力及约束的非对称性，使得在计算的过程中不仅会存在张开型动态应力强度因子K1，还必然会产生剪切型动态应力强度因子K2。利用ANSYS求解完成后，输出裂尖两侧附近节点的位移值，代入K1、K2求解公式，从而计算出瞬态分析各节点每一步的K1i和K2i的值，利用最小二乘法对各步节点的应力强度因子进行线性拟合，外推到r=0即裂尖处的动态应力强度因子[15]。该模型受冲击荷载下的动态应力强度因子分别如图4、图5所示。

从图4、图5中可以发现：

(1) 在0～15 μs左右，K1、K2的值均为零，这是因为试样受到冲击载荷作用产生的应力波传到裂缝尖端需要一段时间；在15 μs之后，K1随着模态角的增加而减小，而K2的绝对值则随着模态角的增加而增大。

图4不同模态下四点剪切复合试样受线性冲击荷载下动态应力强度因子K1和K2

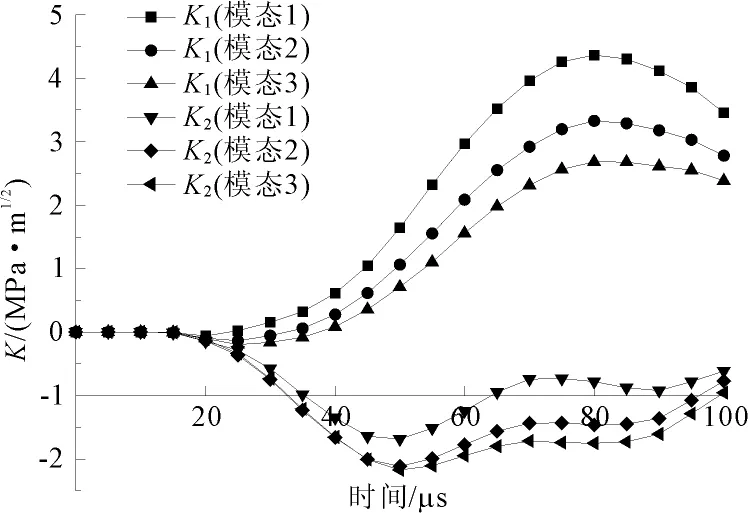
图5不同模态下四点剪切复合试样受正弦冲击荷载下动态应力强度因子K1和K2

(2) 四点剪切复合试样在线性冲击荷载作用下，K1随时间逐渐增大。在40 μs之后不同模态角下的K1的值均基本呈线性增大；而K2的绝对值在线性冲击荷载作用下也随时间逐渐增大，其变化呈现陡-缓-陡趋势，较K1的变化趋势更复杂。

(3) 四点剪切复合试样在正弦冲击荷载作用下，K1先增大后减小。但在模态角较小的情况下，其变化趋势较大，当正弦力在80 μs，即为零时，K1达到最大值，比力达到最大值时要滞后40 μs；而K2的绝对值重复先增大后减小的过程，K2变化趋势同样比K1复杂，在50 μs左右达到峰值，比正弦力达到最大值时也要滞后。

2.2 均质模型验证

利用ANSYS软件对如图6所示的三点弯曲试样模型进行建模，材料的弹性模量E为210 GPa，泊松比ν为0.3，密度ρ为7 800 kg/m3。冲击荷载形式及作用时间均与算例2.1相同，计算时间为100 μs。利用双材料界面理论方法计算该模型在冲击荷载作用下的动态应力强度因子，将计算结果与文献[3]中的结果进行比较。

当使用界面公式计算均质材料的动态应力强度因子时，只需将裂缝两侧设置为同一种材料，即取相同的材料参数进行计算。根据最小二乘法和位移外推的原理，可以得到三点弯曲试样模型受线性冲击荷载和正弦冲击荷载作用下的动态强度因子如图7、图8所示。

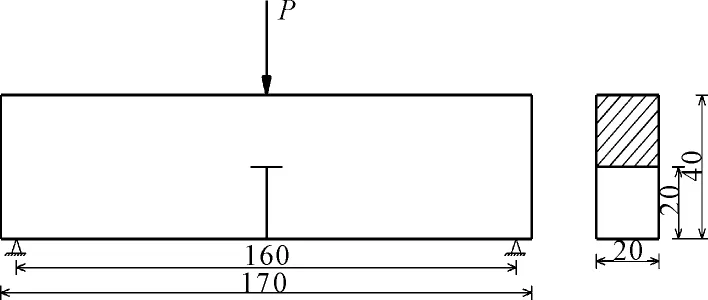
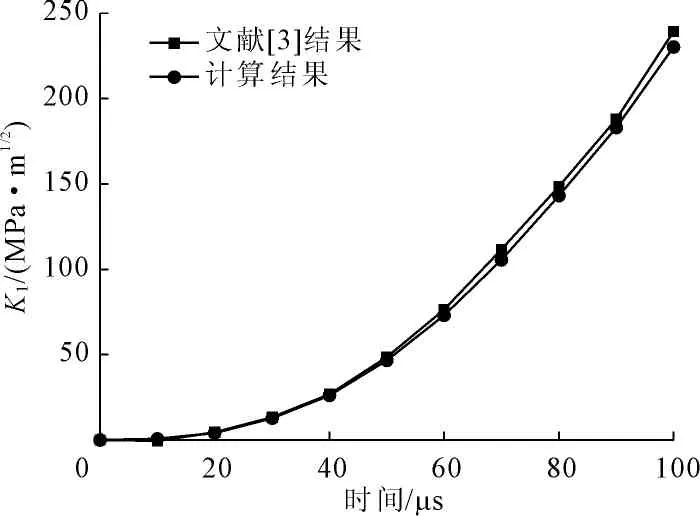
图6 三点弯曲试样模型(单位：mm)

图7线性冲击荷载下动态应力强度因子

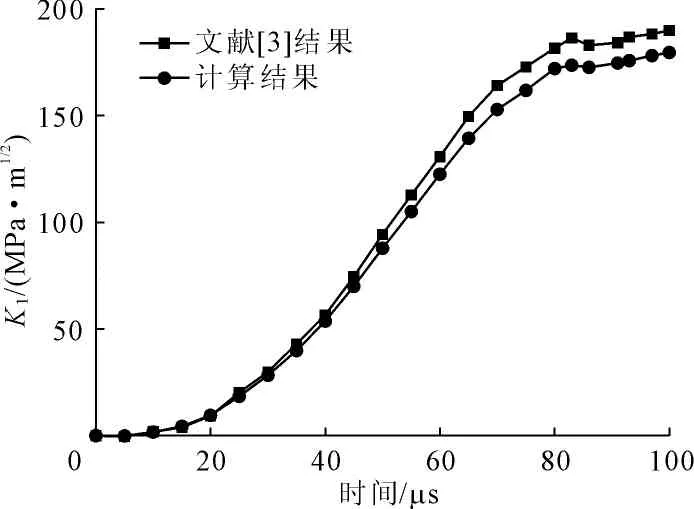
图8正弦冲击荷载下动态应力强度因子

从图7、图8中可以看出，运用双材料界面公式计算出的结果与文献[3]的结果较为接近，表明利用该界面理论方法求解均质材料的动态应力强度因子能够满足一定的精度要求。由于该方法基于双材料界面力学公式，当解决工程实际中复杂的界面动态断裂问题时，该方法便成为一种有效方式。

3 结 论

试样在受到冲击载荷作用的初始时间段内应力强度因子的值为零，这是因为初始应力波从受力位置传到裂纹尖端需要一定时间。试样在冲击载荷下的行为与在静态载荷作用下不同，不是直接把外力随时间变化的最大值代入静态应力强度因子表达式中得到动态应力强度因子最大值，需要对试样加载全过程进行动力响应分析来确定试样的动态应力强度因子。

文中界面应力强度因子公式可以用来计算均质材料三点弯曲试样模型的动态应力强度因子，并满足一定的精度。在进行不同模态下的界面结构动力响应分析时可以发现，K1随着模态角的增加而减小，而K2的绝对值则随着模态角的增加而增大，而且无论是在线性冲击荷载还是正弦冲击荷载作用下，当界面结构受剪切作用时，在计算时间之内剪切型动态应力强度因子K2的变化趋势较张开型动态应力强度因子K1更复杂。