基于双参数强度折减法的优化研究
刘 纯,刘希成,苏立海,李 宁
(1.中国民航工程咨询公司, 北京 100000; 2.空军工程大学, 陕西 西安 710038;3.西安理工大学, 陕西 西安 710048)
现行通用传统强度折减法由于工程实际的深入发展和研究,逐渐暴露除一些缺陷,岩土体强度参数的同步、同量衰减模式无法真正意义上反应边坡失稳过程发生的内在破坏机理,对正确分析边坡稳定性产生了一定的误差,为解决这个问题,工程界长期以来为此进行了大量卓有成效的分析和研究。唐芬等[1-2]认为黏聚力和内摩擦角应采用不同的衰减数值,但是文中缺少相关的理论基础支撑。学者袁维等[3-4]、白冰等[5-6]提出新方法,通过推导验证,补充完善了双参数强度折减法计算边坡稳定性安全系数的理论空缺。Conte等[7]近似地认为边坡土体强度衰减曲线斜率为线性恒值,得到了c、φ强度衰减的解析公式。王强志等[8]和薛海斌等[9]的研究成果未考虑土体强度参数的衰减次序问题,尚待进一步优化。
1 双参数强度折减法
1.1 双参数差异折减的原理
边坡土体材料的强度计算由黏聚力和内摩擦角正切值组成的解析式控制,两者之间的作用关系需要进一步研究和优化[10-13],坡体失稳发生滑动时,c连接链首先断裂失效,当应变逐渐增加时,φ随着颗粒间的滑动发挥作用,为了更加真实的反映c、φ的衰减机制,通过边坡算例做如下探讨。
1.2 双参数差异折减的假设
本章对边坡失稳时岩土体强度参数失效机制进行研究和总结,结合衰减次序间隔系数,提出了适用于边坡稳定性的评价方法。岩土体理想强度软化曲线如图1所示。
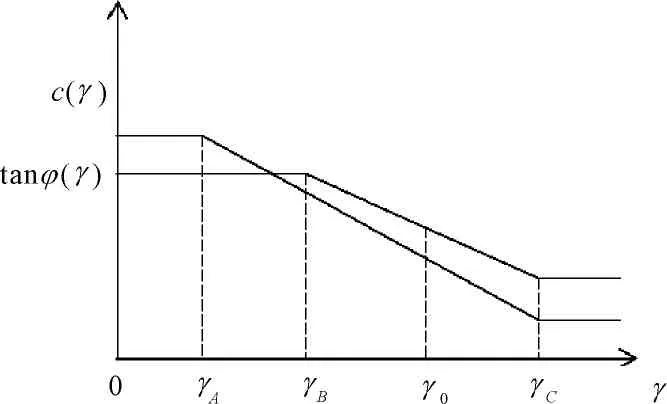
图1岩土体强度参数理想衰减曲线
土体强度参数的失效机制可以通过图1中理想衰减曲线的斜率和特征点很好的反映出来,为进一步推导c、φ差异折减解析公式提供了现实基础。
1.3 双参数差异折减关系推导
基于上述假设根据图1有:
(1)
(2)
通过式(1)和式(2)可见:黏聚力和内摩擦角正切值之间的数学关系可以通过将强度衰减过程理想化处理后的曲线得到,较为全面的反映了边坡岩土体在受到外界荷载和扰动后发生滑坡时,其岩土体材料的强度衰减演变过程,为下一步推演c、φ之间的函数关系奠定了理论基础和现实可能,本节将通过这一假设,对黏聚力和内摩擦角正切值之间的关系进行分析和研究如下:
(3)
(4)
由式(3)和式(4)得:
(5)
γB=aγA
(6)
(7)
将式(6)和式(7)代入式(5)得:
(8)
(9)
(10)
式中:γA、γB、γ0、γC为不同时刻对应的应变量;cA、cB、c0、cC为峰值、tanφ衰减开始、极限平衡状态、残余强度时分别对应的c值;tanφB、tanφ0、tanφC为峰值、极限平衡状态、残余强度时分别对应的tanφ;kc、kφ为黏聚力、内摩擦角的折减系数,即各自的安全系数;a表示岩土体强度参数的衰减次序间隔系数。
2 边坡综合安全系数的选用
双安全系数kc、kφ和边坡综合安全系数ks之间存在必然的关系,唐芬等认为:
ks=(kc+kφ)/2
(11)
Yuan等则认为边坡综合安全系数ks与双折减系数kc、kφ服从关系式:
(12)
Isakov等[14-15]认为边坡综合安全系数的表达式可以表述为:
(13)

关于双安全系数与综合安全系数之间的关系十分复杂,本文根据赵炼恒等[16]的研究,选择Isakov等的研究成果来处理双安全系数kc、kφ和边坡综合安全系数ks之间关系。
3 衰减次序间隔系数讨论
本文结合Dawson等[17]所述的边坡算例,对衰减次序间隔系数a进行讨论,进一步研究岩土体强度参数差异折减情况下边坡稳定性的变化规律。假定c、φ衰减速率恒定,试取a为1.00、1.05、1.10、1.15、1.20、1.25、1.30、1.40、1.60、2.20、3.00时,边坡稳定安全系数的相应变化量,相应结果如表1和表2所示。

表1 ks随a的变化情况表

表2 ks增率随衰减次序间隔系数a的变化表
将表1、表2中的数据反映到图2、图3有:随着a值的增大,ks逐渐增大,但在1.4以后逐渐趋于平缓,表明tanφ相对c有衰减延迟时会对边坡安全系数产生影响,但可以预见的是,当两者之间的衰减间隔达到一定值, 将不再变化,逐渐趋于稳定。
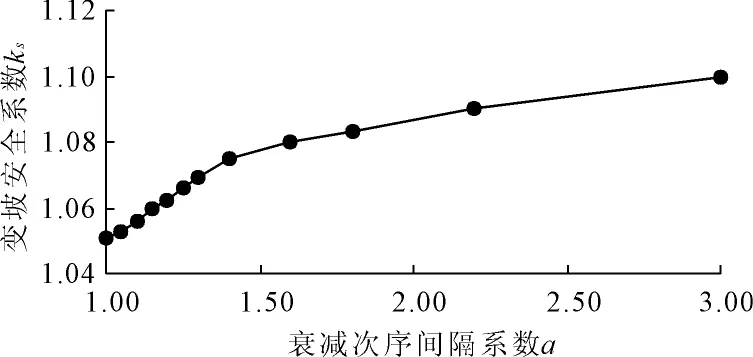
图2边坡安全系数随时间间隔系数的变化曲线
由图3有:随着a值的增大,ks增率可以分为增大、减小和平稳三个变化趋势,其中:ks随a值的增大而逐渐过渡变化,先期增大后减小,并在a=1.6以后,曲线渐趋平稳。

图3边坡安全系数增率随衰减次序间隔系数的变化曲线
综上所述:c、φ衰减的间隔越长,从数据和分析来看,边坡就越稳定,符合本文预测。
为进一步研究a值工作效果,本节选取a=1.00、1.00
1.00 a=1.25,ks增长速率到达峰值最敏感点。 1.25 a=1.60,ks增长速率开始趋于恒定。 a>1.60,ks增长速率趋于稳定并至一恒定值。 结合上述计算结果,本文认为:当1.00 (1) 本文推导了考虑c、φ衰减次序间隔的双参数强度折减解析公式[18],通过算例的分析和验证,建议在评价边坡稳定状况时,可以尝试将过去单一安全系数描述边坡稳定的方法加以改进,将安全系数表述为一个区间范围,以达到弹性评价目标边坡稳定性的目的。 (2) 现阶段关于边坡稳定性分析时a值得研究并不常见,相关结论并不完善,所以仍有很大空间去深入的讨论和研究a值的取值范围和作用机制。4 结 论

