“有的放矢”，让数学课堂追问更有效——以“小数加减法”为例

□王灵勇

数学课堂中教师的追问是启发式教学的重要手段，但“过频”“过浅”“偏离目标”“散乱”的课堂追问，对学生的学习有百害而无一利。要有效进行“追问”，教师应了解学生真实的思维过程，让学生关注学习过程，实现自主学习，体验思考的美妙。下面笔者以“小数加减法”一课为例，提出有效课堂追问的具体策略，和大家一起交流。

一、围绕教材内容，理清追问脉络

数学课堂中什么时候追问，用怎样的方式追问，这是由教学内容所决定的。教师必须理清教材的脉络，梳理教材中的追问点，做到心中有数。笔者在实践中对教材的教学内容进行了整理分析，完成了数学教材追问点的整理。备课时，先找出内容的关键处、重难点处、疑惑处、提升处、盲点处、易错处等，然后进行追问设计。根据不同的教学内容，笔者整理出以下主要的追问方式。

·因果追问。比如计算课，对算理的理解，追问“你是怎么知道的”“为什么”“你是怎么想的”“错在哪里”等问题，可以让学生明因果。

·发散追问。在一题多解、算法多样、学生举例等环节中可以采用发散性追问，追问“还有不同的方法吗”“你更喜欢哪种方法”“这种方法好在哪里”等。这类追问可以使学生既知其一，又知其二，有助于培养学生的发散思维。

·跟踪追问。根据教学重难点设计一个问题，学生回答之后，教师接着追问几个子问题。这种方式的追问可以培养学生的探究习惯。

·逆向追问，即反问。引导学生从不同的角度分析存在的问题，培养学生的思辨能力和批判思维。

此外，教学中还可尝试教师追问、教师引导学生追问、教师引导学生互问互答等追问方式。

二、围绕核心目标，设计递进问题

1.精心设计中心问题。

每节课教师都要根据教学目标，精心设计几个中心问题，以此展开追问。

2.精心设计子问题。

为了顺利解决中心问题，根据新旧知识间的联系以及学生学习的难点等，可以设计追问的1级子问题，为解决1级子问题，还可以设计追问的2级子问题等，形成有层次性的问题脉络。

如笔者在“小数加减法”一课中，进行了如下一系列的追问。

①今天我们学习小数加减法，大家已经认识了小数，小数加减法该怎么计算呢？又为什么这么算？②你能以米为单位表示118 厘米软尺的长度吗？③（出示第一幅尺子图）这是几米？④（出示第二幅尺子图）这是几米？⑤（出示第三幅尺子图）这又是几米？⑥这把尺子缺了一截，想知道剩下有多长，有什么办法？能列式吗？（每人动手）⑦1.18-0.76，这样一位对着一位减的方法，你觉得陌生吗？什么时候用过？⑧你发现小数加减法和整数加减法有什么不同？⑨你觉得他说得怎么样？谁能用一句话概括起来说？⑩小数加减法还有哪些新情况呢？看谁编的题目能给大家带来新情况。（独立思考编题）⑪（指着3.74+0.8）你看出什么新情况了？（独立计算）⑫以前加减法都是末位数字对齐，这道题目为什么不末位对齐呢？⑬为什么一定要小数点对齐，相同数位才对齐？⑭刚才这题让我们收获很多。（指着3-0.6）你又发现什么新情况？（试做中找出对比）⑮一样的题，结果却不一样，哪个对呢？⑯你们给整数后面填上小数点和0，根据是什么？⑰那第二种是什么原因做错了呢？⑱同学们还编出很多好题，（指着9.65-8.75=0.90）结果是怎样的数？（引导化简）⑲还有呢！（指着24.23+14.77）这道题的结果怎么表示呢？根据什么？（引导简写）⑳同学们通过编题，回顾刚才自己做过的题，你发现小数加法和减法在计算的时候要注意什么？

从实践结果看，完成新知教学总共只进行了20 次追问，大大提高了课堂效益。问题之间的层次关系如下:

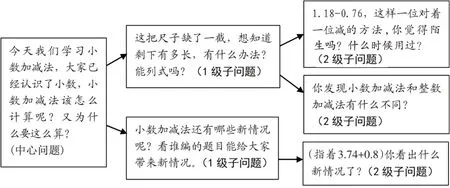
三、引领主动追问，提升思维层次

通过教学实践发现，运用“六学”教学模式能有效培养和提高学生的追问能力。“六学”是指：导学—试学—展学—研学—固学—延学。学生先学、先试、先交流，教师的指导与讲解、师生的共同研讨全部置后。“展学”主要是让学生展示活动成果、讲解思路、提出困惑、生生质疑互动。“展学”最大的亮点是“小先生”上台讲学，学生间的交流通过互相提问、主动追问的方式进行。教师要大胆放手，适时引导，让学生在主动追问中思考，在思考中感悟，在感悟中深入，以此提升思维层次，促进学生思维的有效形成。图示如下：

例如师（指着3.74+0.8）追问：你看出什么新情况了？请用自己喜欢的方法来解决这道题，将你们的思考过程记录下来（生独立计算）。

几分钟后学生将自己的作品呈现在黑板上，接着进入主动追问环节。

师：同学们对黑板上的这些作品有什么想说的吗？

生6 对生5 追问：你为什么把4 和8 对齐加？7和0对齐加？

生5：和整数加法一样，4 和8 都是最低位要对齐。

生6追问：如果是钱的话，3.74元，4表示的是4分，0.8 元，8 表示的是8 角，单位不同能进行相加吗？

生5：哎呀！我弄错了。

生7对生1追问：这种方法你是怎么想的？

生1：我用学过的方法计算，3.74里面有374个0.01，0.8里面有80个0.01，总共有454个0.01，等于4.54。

师引导：用转化为已经学过的知识解决问题，这也是一种好方法。

生8对生2追问：你这种方法是怎么想的？

生2：我是用乘法分配率来解决的。

生8 追问：整数中学过乘法分配律，在小数中还没学过，没有证明过怎么能确定可以呢?（生2用疑惑的表情看着老师）

师引导点拨：这位同学的想法很好，但是乘法分配率这一定律在小数范围内是否适用确实还需要我们进一步进行验证。

生9 对生3 追问：你给0.8 后面添上0，根据是什么？

生3：小数末尾添上0大小不变。

生10对生4追问：0.8后面不添0行吗？

生4：行。

生3：不行。

师引导：其实不添0 也行，我们刚刚学习小数加减法，建议大家还是添上，这样就变成了末位对齐的情况，不容易出错。

生7 对生1 的追问和学生的释疑，强化了运用转化的思想解决新知识的意识，对全班学生都有启发作用。生2的方法，让学生对知识的理解产生了个性化、创造性的见解。生8 对生2 的两次追问加上教师及时进行梳理、提炼和提升，让学生明确整数乘法分配律，在小数范围内是否适用需要进一步进行验证，感受到数学方法的严谨。又如生3、生4、生5的方法，小数的运算是否可以类比整数的运算，很多学生心存“混沌”，正是学生精彩的追问、教师的点拨帮助他们从混沌走向清晰。

四、适时巧妙追问，培养思维品质

“研学”是指教师启发下的师生共同学习。其过程是：教师设问—学生再思考（或再活动）—抽象概括（或数学化符号化）。研学环节，教师要抓住时机，通过针对性的追问，培养学生的思维品质，实现对新知的理解。

（一）回答正确时追问——提升理解

在学生回答正确时，利用针对性的追问将学生的学习引向深处，加深学生对数学的理解。

如针对生3、生4两种正确的竖式计算方法，教师追问：以前加减法都是末位数字对齐，这道题目为什么不末位对齐呢？

生：整数的末位是个位，末位对齐就是个位对齐。但是小数不一样，小数部数位不同的末位就不一样，不能末位对齐。应该小数点对齐。

师追问:为什么要小数点对齐，相同数位才对齐？

生：举个例子，比如长0.8 米和3.74 米，如果把8和4相加，就是把8分米和4厘米相加，肯定错了。

师：这位同学用长度的例子说明小数加减法中深刻的运算道理，也就是说只有相同的计数单位，它们的个数才能相加减。

师小结：其实小数点对齐和整数的末位对齐本质上是一样的，都是确保相同数位对齐。

（二）回答错误时追问——巧妙纠错

当学生回答错误时，教师不要直接否定，更不要直接告知准确答案，而要巧设富有启发性的追问，引导学生的思考逐渐深入、全面，并自行纠错。

如前面提到的问题⑭：“刚才这题让我们收获很多。（指着3-0.6）你又发现什么新情况？”（试做中找出以下两种对比）

师追问：一样的题，结果却不一样，哪个对呢？

生：第一个对，因为在十分位上是0 减6，所以十分位应该得4而不是6。

师追问：你们给整数后面填上小数点和0，根据是什么？

生：小数的性质。

师追问：那第二种是什么原因做错了呢？

生（做错的学生）：我没有添上小数点和0，想成0加6得6了。

师小结：别看这小小的0，添上它一眼就看出是几减6，而且变成可以末位对齐的情况了，这位同学第一次做这样的题，他的错误给了我们重要的提醒。

（三）比较异同时追问——融会贯通

教师要善于抓住知识与方法之间的联系，在比较异同中利用追问，帮助学生将所学的数学知识融会贯通，改变学生思维的孤立性和局限性。

如前面提到的问题⑦：“这样一位对着一位减的方法你觉得陌生吗？什么时候用过？”

教师在让学生比较小数加减法和整数加减法的不同时追问了问题⑧：“你发现小数加减法和整数加减法有什么不同？”

在比较小数加法之间的不同时追问了问题⑪：“（指着3.74+0.8）你看出什么新情况了？”

在与整数加减法区别时追问了问题⑫：“以前加减法都是末位数字对齐，这道题目为什么不末位对齐呢？”

教师在让学生梳理小数加法和减法的计算方法时，追问了问题⑳：“小数加法和减法在计算的时候要注意什么？”

（四）思维受阻时追问——水到渠成

学生思维遇到障碍时，教师要设计循序渐进的追问，帮助学生开拓思路，这也体现教师的教学智慧和功底。如“小数加减法”一课的挑战题。

小马虎做一道一位小数的加法题，把第一个加数个位8 看成了4，把第二个加数十分位的3 看成了6。计算结果是17.5，正确的计算结果是多少？

第一次出现该题，绝大部分学生都无从下手。教师进行了以下引导。

师:加数个位上的8表示什么？4表示什么？生：表示8个1和4个1。

师追问：8个1看成4个1，你发现了什么？

生：少算了4。

师追问：十分位的3表示什么？6表示什么？生：表示3个0.1和6个0.1

师追问：你又有什么新的发现呢？

生：哦！十分位多算了0.3。

师追问：个位少了4，十分位多了0.3，结果怎么变？

生：先补上4，再减去0.3。

生：结果少了3.7。

生：把17.5，补上少算的4，减去多算的0.3，就是17.5+4-0.3=21.2。

教师的层层追问，让学生通过数的“位值制”意义，明确加法中少算要补、多算要减的道理，答案自然水到渠成。