基于直流电动机回馈能量的电流控制Boost变换器特性研究
杨艳,任康成,姚肖勇,武洲
(常州星宇车灯股份有限公司,江苏常州 213022)
0 引言
开关变换器中各种非线性现象及其产生机制得到了广泛的关注和研究[1-7],相应的研究结果对设计更加稳定、可靠的开关电源起到了极大的促进作用。此外,相关研究还可用于探测开关变换器中产生不稳定现象的原因。同样,对于非线性行为的研究也有助于混沌理论在开关变换器的应用探索。
晶闸管可控整流装置带直流电动机负载组成的系统(晶闸管直流电动机系统)是一种主要的电力拖动系统,也是可控整流装置的主要用途之一。随着交流调速的广泛应用和巨大优势,直流调速虽已呈被淘汰之势,但仍有大量直流调速系统投入运营。在电机及其他动力系统的实验中,有大量能量转化为热能被浪费。如何将这些再生的电能回馈给电网,对降低电机的整体能耗、节约能源仍是十分关键的课题,因此对直流电动机回馈能量的电流控制Boost变换器特性进行研究具有重要意义。
近年来,针对电流控制开关DC-DC变换器中存在的次谐波振荡[6-8]、准周期[9]、分岔[10-14]等非线性现象,对其开展了大量的研究工作,相应的研究结果对设计更加稳定、可靠的开关电源起到了极大的促进作用。已有相关文献资料,通过建立离散映射模型,研究了电路参数对分岔及混沌产生的影响。然而,对于变换器用于直流电动机传动应用方面的文献鲜有报道。Boost变换器用于直流电动机传动时,通常是用于直流电动机再生制动时将电能回馈给直流电源。本文作者在传统电流控制型Boost变换器基础上,将直流电动机进行耦合用于回馈能量,将二阶电路转化为一阶电路,构成了直流电动机回馈能量的电流控制Boost变换器,并进行新电路状态方程的精确离散模型建立,利用MATLAB仿真平台得出相关电路参数相对应的分岔图,并分析电路参数变化对该变换器动力学行为的影响。
1 直流电动机回馈能量的电流控制Boost变换器离散时间映射模型
图1所示为直流电动机回馈能量的电流控制Boost变换器原理图。其主电路是由Boost变换器改进而成,电动机的反电动势Em相当于原电路中的电源,而此电路中的直流电源E替换了原有的负载,R为电动机电枢回路电阻与线路电阻之和,因直流电源的电压可视为恒定,故无需并联电容器。控制电路则由比较器、RS触发器、时钟脉冲CP构成[4]。
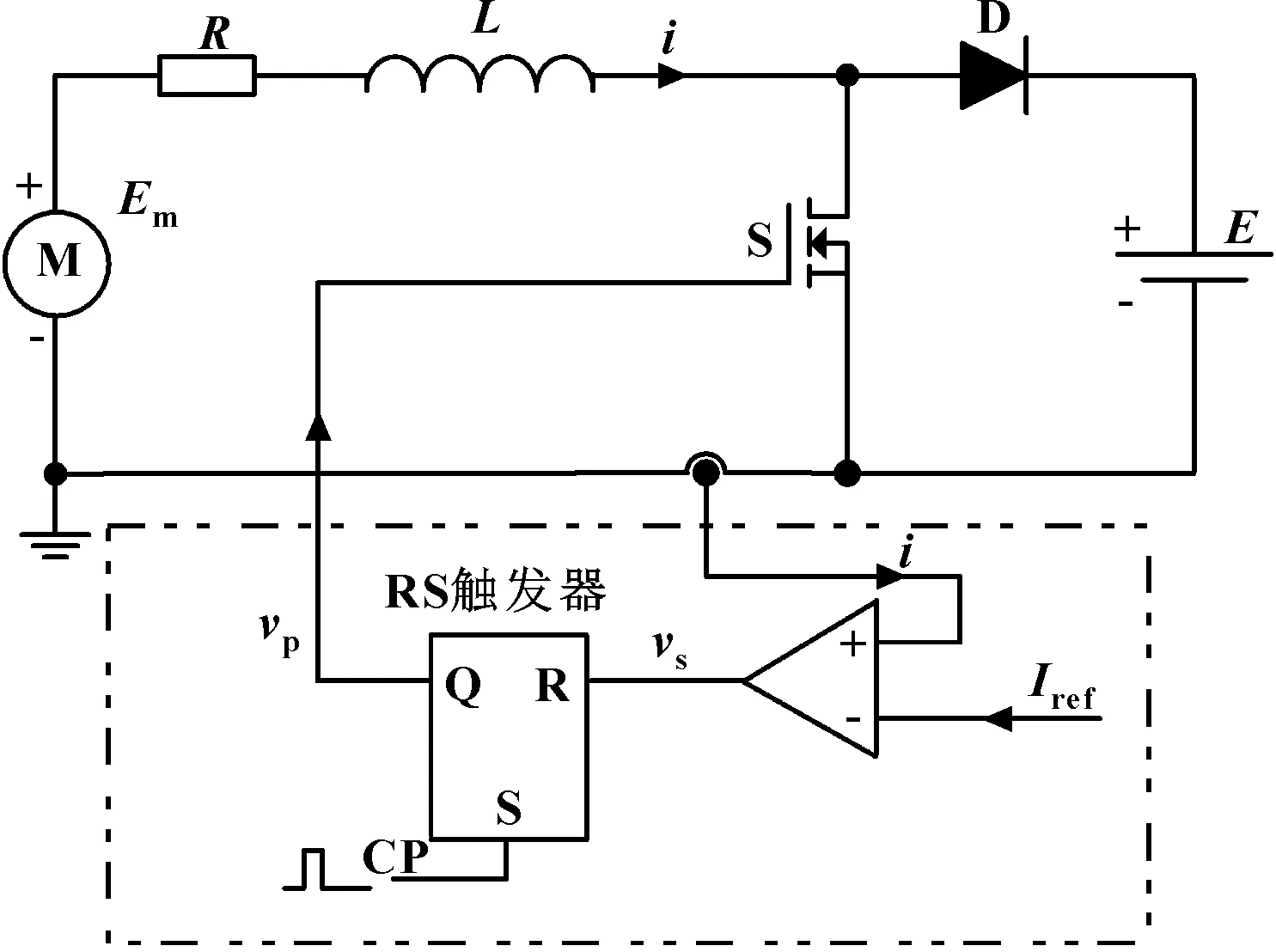
图1 直流电动机回馈能量的电流控制Boost变换器原理图
当时钟信号到来,开关管S导通,当采样电感电流i上升到参考电流Iref时,开关管S由导通状态进入关断状态,而后,采样电感电流i下降,转换到下一个开关周期。若在整个开关周期内,电感电流i未下降到零值,则变换器工作在电感电流连续导电模式(Continuous Conduction Mode, CCM),下降到零值时,则变换器工作在电感电流断续导电模式(Discontinuous Conduction Mode, DCM)。
如图2所示为开关管两端电压v与电感电流i的时域波形图。在第n个开关周期内,t=t0=nT为初始时刻[4-5],t1、t2分别表示开关管S导通与关断的瞬态时间点,t3为该开关周期的截止点。τ1=t1-t0、τ2=t2-t1和τ3=t3-t2分别为3种不同开关状态内的持续时间。状态变量在t=t0=nT为该开关周期的初值,用xn=in表示;在t=(n+1)T时刻为该开关周期的终值,用xn+1=in+1表示。

图2 开关管两端电压v与电感电流i波形示例
根据开关管S和二极管D的不同工作状态,则改进型Boost变换器存在3种开关状态,分别对应3种不同的电路拓扑,如图3所示。当Boost变换器工作在CCM模式,存在开关状态一和开关状态二;当Boost变换器工作在DCM模式,仅存在开关状态三。

图3 不同开关状态对应的电路拓扑
(1)开关状态一:开关管S导通,二极管D关断。电动机的反电动势Em放电,电感电流i增大。即
(1)
相应的时域解为
(2)
式中:a=L/R。
(2)开关状态二:开关管S关断,二极管D导通。电感电流i逐渐减小。即
(3)
当i=Iref时,直流电动机回馈能量的Boost变换器进入开关状态二。在式(2)中代入t=τ1,得i1(τ1) =Iref,算出开关导通时间τ1为
(4)
时域解为
(5)
(3)开关状态三:开关管S关断,二极管D关断。电感电流i恒为零,这时的状态方程为
(6)
在Boost变换器进入开关状态三时,则电感电流i下降为零,即i2(τ2)=0。在式(5)中代入t=τ2,可求出开关状态二区间的持续时间为
(7)
式中:m=Em/E。
相应的时域解有
iL3(t)=0
(8)
直流电动机回馈能量的Boost变换器工作时的电感电流边界情况如图4(a)和4(b)所示,故电流控制Boost变换器从xn到xn+1有3种可能的离散映射,分别表示为
(1)当in≤Ib1时,开关管S处于导通状态。整个开关周期内,Boost变换器只有开关状态一,到该开关周期结束时,其离散时间映射模型为
(9)
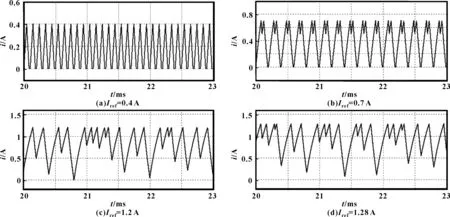
(2)当Ib1 (10) (3)当in≥Ib2时,电感电流i下降到零,则Boost变换器将工作于DCM。此时,Boost变换器经历了3种开关状态,其状态的转变过程为xn→x(τ1)→x(τ2)→xn+1。相应的离散时间映射模型为 xn+1=f3(xn)=0 (11) 图4 两个电感电流边界的示意图 3种离散映射由两个边界情况划分,对于边界Ib1,由图4(a)可知,Boost变换器只经历了开关状态一,把in+1=Iref和in=Ib1代入式(9)解得 (12) 对于边界Ib2,由图4(b)可知,Boost变换器依次经历了开关状态一和开关状态二,把in+1=0和in=Ib2代入式(10)解得 (13) 综上所述,式(9)—(11)构建了直流电动机回馈能量的电流控制Boost变换器的离散时间模型,该模型为一维离散系统,整理写成如下形式: (14) 电路参数E=9 V,Em=8 V,Iref=1.2 A,L=800 μH,R=3.5 Ω和T=100 μs。根据第1节所建立的直流电动机回馈能量的电流控制Boost变换器离散映射模型,采用该电路参数,利用MATLAB仿真软件编程,分别以输入电压E和参考电流Iref为可变参数,记录每个导通时间开始时刻的电感电流采样值i,可作出直流电动机回馈能量的电流控制Boost变换器随输入电压E和参考电流Iref变化的分岔图分别如图5(a)和图5(b)所示。图中两条电感电流边界分别用Ib1、Ib2表示。 图5 随输入电压E和参考电流Iref变化时的分岔图 图5(a)中,Iref=1.2 A,E=9~18 V。当E较小时,电动机回馈能量的电流控制Boost变换器工作在稳定的CCM周期1状态,随着电压E的增大,在E=9.7 V附近,Boost变换器的电感电流与边界Ib1发生了边界碰撞,产生了倍周期分岔,Boost变换器的运行轨道由CCM周期1状态进入到CCM周期2状态。随着电压E的进一步增大,当E=13 V时,Boost变换器电感电流再次与边界Ib1相遇发生了边界碰撞,Boost变换器进入到混沌状态。电压E继续增大,在E=15.6 V点处,Boost变换器的电感电流与边界Ib2发生了新的边界碰撞,Boost变换器将进入DCM混沌状态。当E处在13~15.6 V之间,即电感电流与边界Ib1两次碰撞间,Boost变换器工作在CCM鲁棒混沌状态[7-12]。当E处在15.6~18 V之间,即电感电流与边界Ib2发生碰撞后,Boost变换器将工作在DCM阵发混沌状态(即由周期窗和混沌状态交替出现)。 图5(b)中,E=16 V,Iref=0.4~1.3 A。可知,随着Iref增大,Boost变换器从最初的稳定DCM周期1状态在Iref= 0.492 A附近与电感电流边界Ib2相遇发生了边界碰撞分岔后进入DCM周期2。随后在Iref=0.81 A处,电感电流与边界Ib1碰撞产生折叠,而后又一次在Iref=0.94 A与边界Ib2碰撞进入DCM周期4。约在Iref=1.11 A处,Boost变换器电感电流再次与边界Ib1发生边界碰撞分岔,由DCM周期4进入到DCM阵发混沌状态。当电感电流增加到约1.25 A时,该运行轨道最后一次与Ib2相遇发生了边界碰撞,由DCM阵发混沌状态转为CCM鲁棒混沌状态。 利用PSIM仿真软件,搭建直流电动机回馈能量的电流控制Boost变换器仿真电路,选用图4的参数进行电路仿真,检验第2节分岔分析的准确性。 当输入电压分别为9、11、15和17 V时,直流电动机回馈能量的电流控Boost变换器对应的时域波形图如图6所示。图6(a)中,E=9 V,从时域波形图可以看出,Boost变换器工作在稳定的周期1状态;图6(b)中,E=11 V,Boost变换器工作于稳定的周期2状态;图6(c)中,E=15 V,Boost变换器工作在CCM混沌态;图6(d)中,E=17 V,Boost变换器工作在DCM混沌态。 当参考电流分别为0.4、0.7、1.2、1.28 A时,直流电动机回馈能量的电流控Boost变换器对应的时域波形图如图7所示。 图6 不同输入电压对应的时域波形图 图7 不同参考电流对应的时域波形图 图7(a)中,Iref=0.4 A,可以看出,Boost变换器工作在稳定的DCM周期1状态;图7(b)中,Iref=0.7 A,Boost变换器工作在不稳定的DCM周期2状态;图7(c)中,Iref=1.2 A,Boost变换器工作在DCM混沌态;图7(d)中,Iref=1.28 A,Boost变换器工作在CCM混沌态。 图6和图7所使用的不同参数值仿真的时域波形,分别对应图5(a)和图5(b)分岔图中典型的参数值,PSIM电路仿真结果验证了分岔行为的准确性,表明了输入电压E和参考电流Iref取不同的参数(增大输入电压E和参考电流Iref的值),直流电动机回馈能量的电流控制Boost变换器将工作在多种状态(稳定的周期状态、次谐波振荡状态、混沌状态等不同的非线性现象[4-7])。 通过构建直流电动机回馈能量的电流控制Boost变换器离散时间映射模型,基于该模型,系统地研究了该控制器的分岔行为及其稳定性,随输入电压或参考电流增大时,发生了边界碰撞分岔现象,从而引起状态失稳。结果表明:直流电动机回馈能量的电流控制Boost变换器的分岔行为是由边界碰撞引起的,当电路参数发生变化时,则该变换器将工作在多种周期状态和混沌状态,文中的研究结果可以有效地指导其电路参数的选取。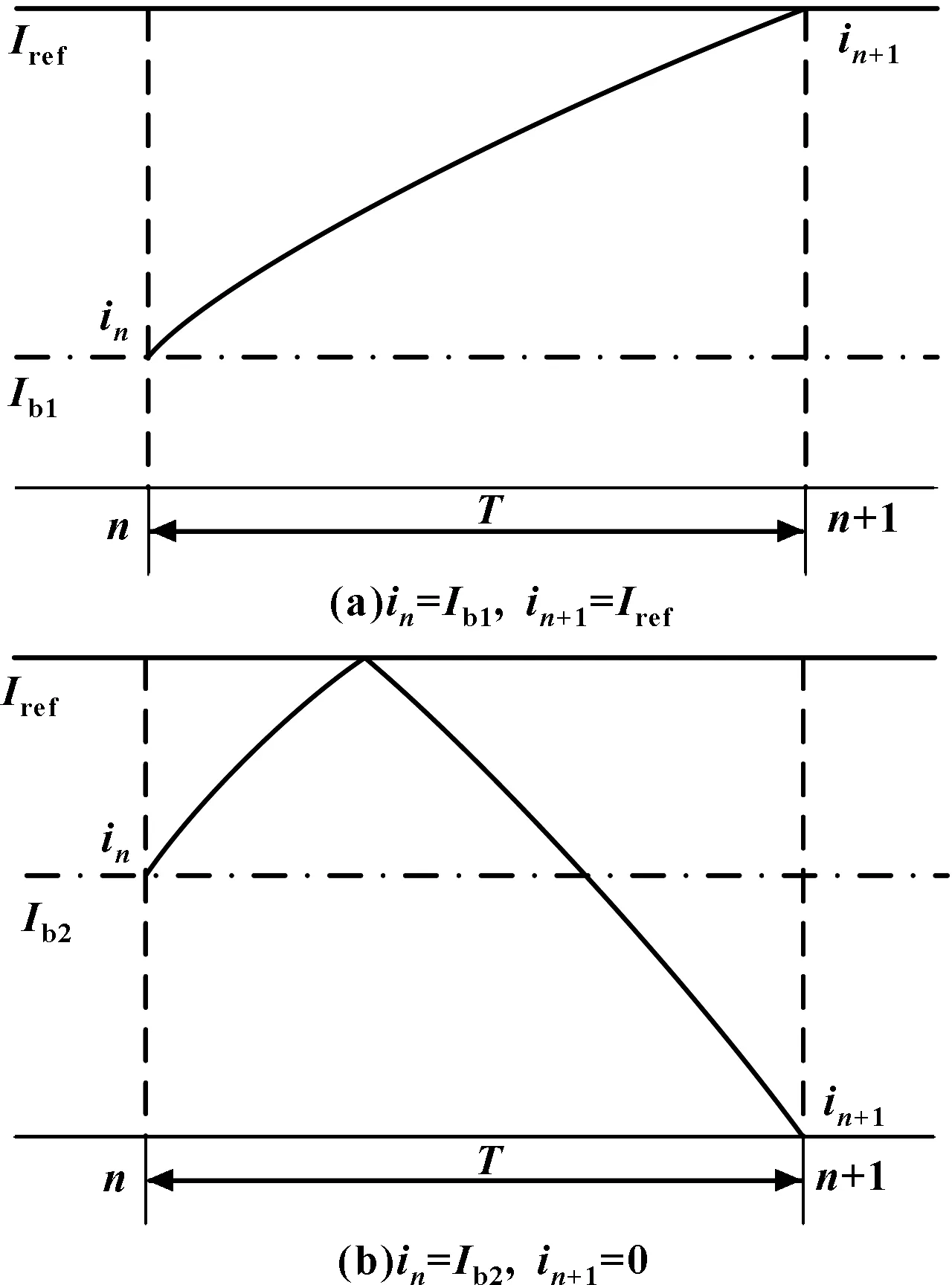
2 基于输入电压与参考电流的分岔分析
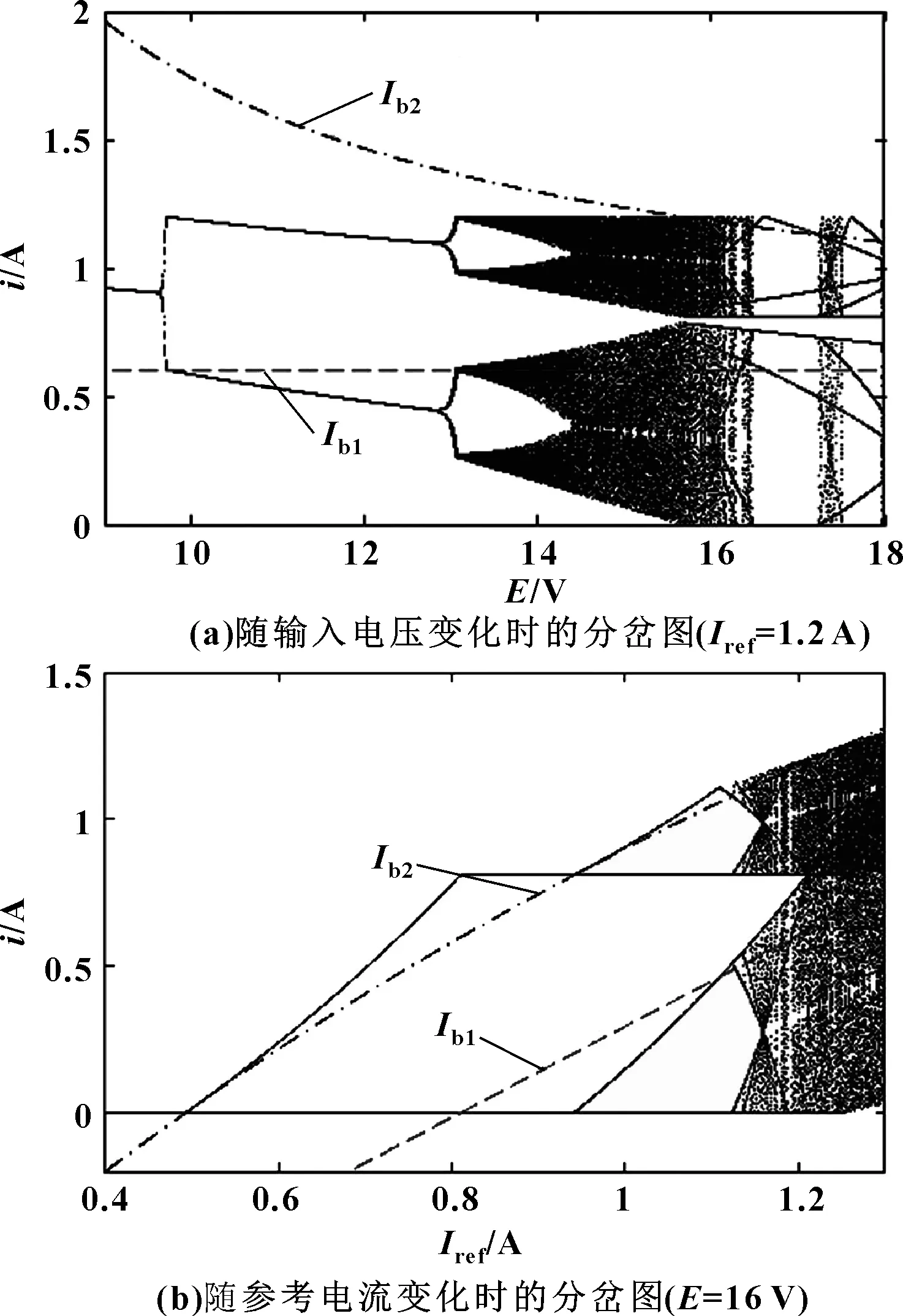
3 电路仿真验证
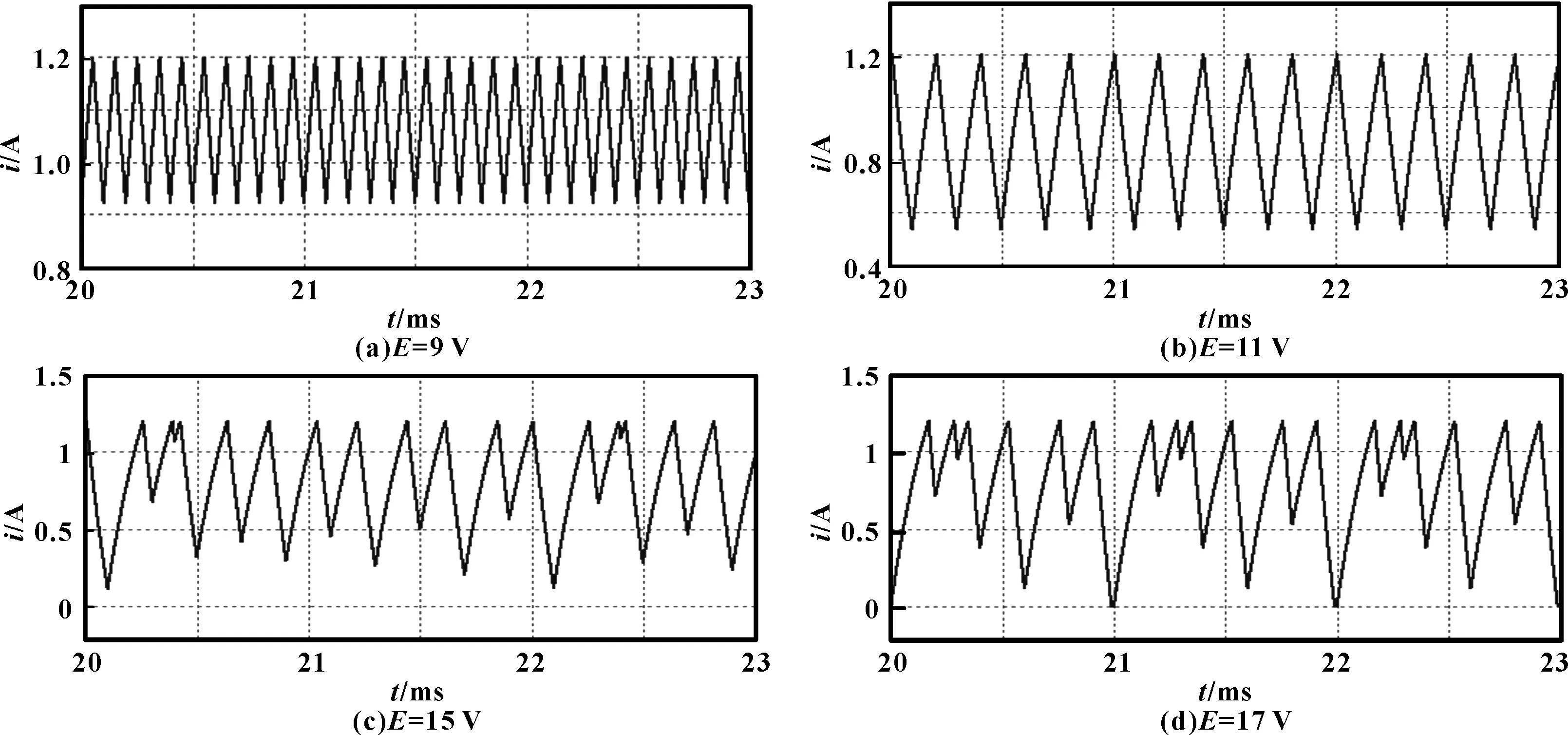
4 结论

