基于直觉模糊集的城市供水安全预警评价模型*

王 威，宋 卓，刘晓然，刘朝峰

(1.北京工业大学 抗震减灾研究所，北京 100124；2.北京工业大学 建筑与城市规划学院，北京 100124； 3.北京建筑大学 理学院，北京 102616；4. 河北工业大学 土木与交通学院，天津 300401)

0 引言

城市供水是城市基础设施的重要组成部分[1]，城市供水安全发生问题不仅会造成巨额经济损失，同时也会给居民生活造成不便，影响城市安全可持续发展。

在对城市供水安全的理解上，国内外学者[2-3]对安全性评价进行了研究，取得了一定成果[4-6]。杨龙江等[7]在建立指标体系的基础上，采用可变模糊评价模型得到城市灾害危险等级、易损性等级、承灾能力等级3方面的评价结果，综合3方面的结果计算出城市综合防灾减灾能力；赵志峰等[8]针对粗糙集应用和熵权计算法不足，提出结合两者特点进行指标权重计算，增加了权重分析的应用性和可靠性；其他的权重确定方法还有属性层次模型法[9]，层次分析法[10]等。宋松柏等[11]根据已有的评价等级标准生成足够数量的指标序列，然后应用BP网络模型建立人工神经网络评价模型，纵观整个过程，人工神经网络法不稳定且运算较繁琐。魏光辉[12]在建立多指标体系的基础上，进行灰色关联分析，并引入熵值法确定指标权重，然后计算关联度，形成了基于熵权的灰色关联模型。

基于此，本文采用直觉模糊集理论[13,15]确定主客观组合权重，进而建立城市供水安全预警评价直觉模糊集模型，并分析了指标权重影响的灵敏度。

1 直觉模糊集评价模型

1)确定属性集和方案集。设城市供水安全预警评价的多属性决策方案集为S，属性集为X，即：

S={s1,s2,…,sk,…,sK}

(1)

X={x1,x2,…,xn,…,xN}

(2)

方案sk(k=1,2,…,K)关于属性xn(n=1,2,…,N)的属性值表示为Ank，所有属性值用矩阵简记为G=(Ank)N×K。

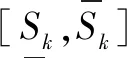
s1s2s3

(3)

3)直觉模糊权重的确定。设城市供水安全预警评价指标的主观权重为：

α=[α1,α2,…,αN]

客观权重为：

β=[β1,β2,…,βN]

则以直觉模糊集方式表达的组合权重[14]为：

ωn=〈min(αn,βn),1-max(αn,βn)〉

(4)

式中：ωn为以直觉模糊集方式表达的组合权重；ρn，τn分别为属性xn∈X的重要性程度和非重要性程度，且0≤ρn，τn≤1。

4)城市供水安全预警评价模型。计算模型如下：

而云南蒙自石榴的在这方面做的比怀远石榴好。在生活中会发现，怀远石榴在蚌埠市内出现的较多，而安徽许多城市多数地区卖的都是蒙自石榴而不是怀远石榴。有许多安徽省内的人甚至不知道怀远产石榴，却知道远在云南的蒙自石榴，这是一个值得深思的问题。

(5)

(6)

(7)

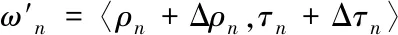
(8)

由式(8)计算出Δρn，Δτn的范围，反映了指标的灵敏度。

2 实例评价

2.1 城市供水安全预警评价指标及标准

根据年鉴数据，本文以2006—2017年郑州市的供水安全数据为基础进行实例分析。城市供水安全预警评价从供水状况、输水状况、用水状况、净水状况4个环节选取12个评价指标构建了城市供水安全预警指标体系，具体情况如表1所示[2，16]。并且将预警等级划分为Ⅰ级、Ⅱ级、Ⅲ级、Ⅳ级、Ⅴ级共5个等级，其每1个等级依次对应的“无警”、“轻警”、“中警”、“重警”、“巨警”5种状态。

根据国家标准、相关部门规定以及国内外研究形成了城市供水安全预警评价指标的分级标准，见表2。

2.2 直觉模糊集评价模型应用

1)确定组合权重。由公式(4)求得的直觉模糊组合权重见表3。

表1 城市供水安全预警指标体系Table 1 Early warning indicators system for urban water supply security

表2 预警指标等级的评价标准Table 2 Evaluation criteria for early warning indicators

表3 指标权重值Table 3 Weight of each index

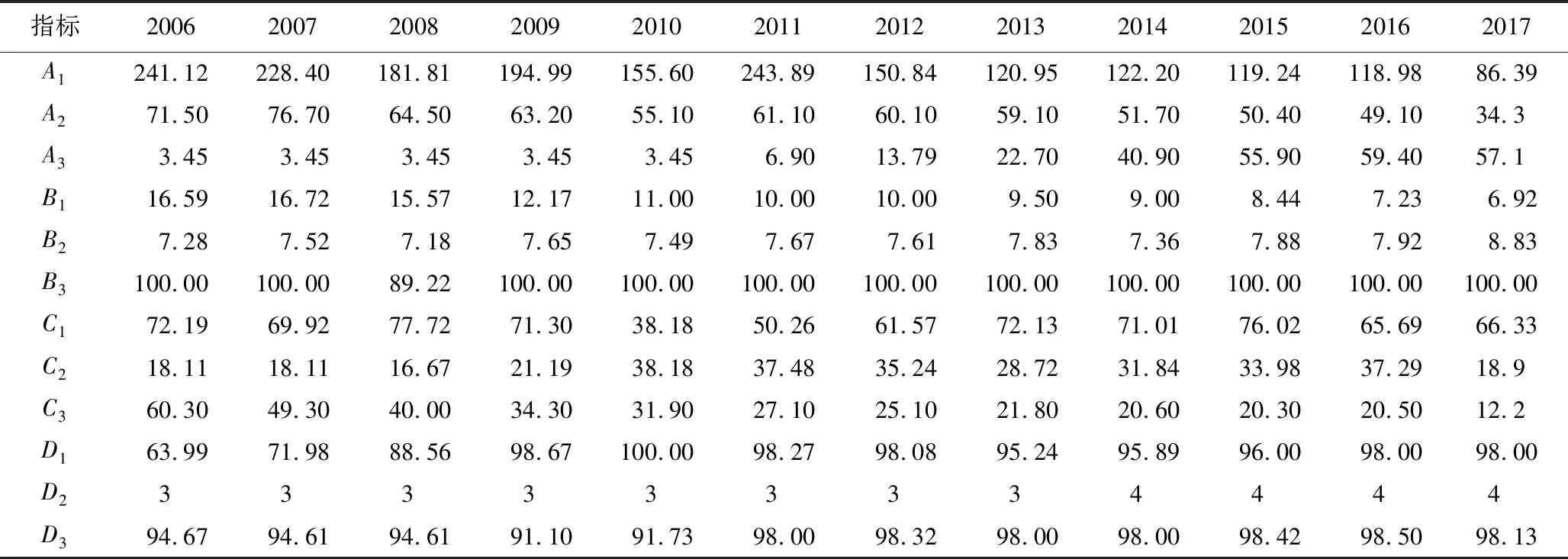
表4 2006—2017年郑州市供水安全预警指标数据Table 4 Water supply safety early warning indicators for Zhengzhou city from 2006 to 2017

根据公式(3)计算直觉模糊集决策矩阵F为：

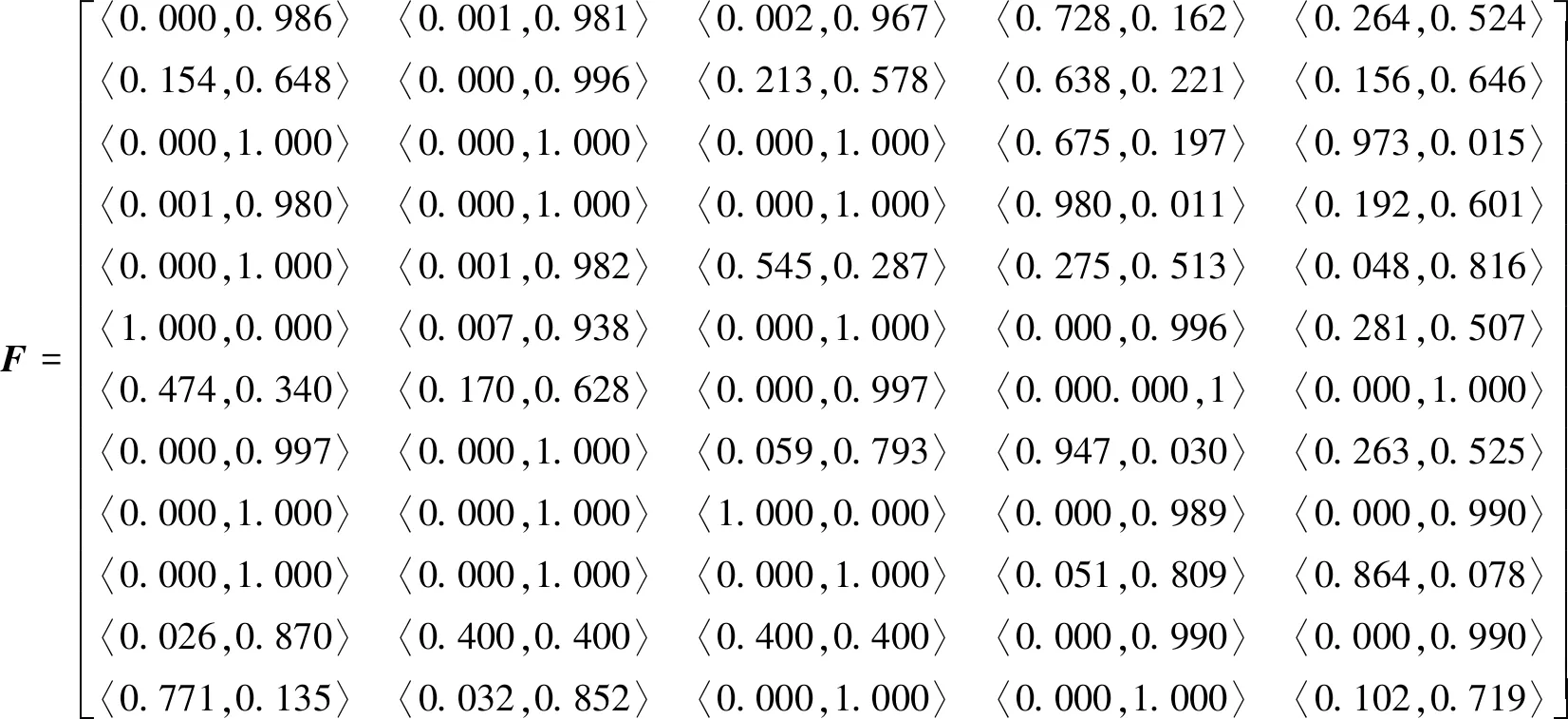
根据公式(6)计算样本综合平均值：V1=〈0.101,0.788〉，V2=〈0.046,0.789〉，V3=〈0.094,0.704〉，V4=〈0.297,0.566〉，V5=〈0.231,0.617〉。

根据式(7)得到样本直觉模糊数得分值：

对2006年样本的直觉模糊数得分值进行大小排序，根据排序结果，可得城市供水安全预警评价等级M1(V4)>M1(V5)>M1(V3)>M1(V1)>M1(V2)，从得分值排序可以得出Ⅳ级最大，Ⅱ级最小，根据直觉模糊理论可知，样本的直觉模糊数得分值最大的对应评价等级即为样本预警评价等级，因此2006年样本的城市供水安全预警评价等级应为Ⅳ级，即进入“重警”状态，表明城市供水系统状态较不安全。

将直觉模糊集理论与物元可拓法的评价结果进行对比分析，结果验证了基于直觉模糊集理论构建的城市供水安全预警评价模型具有可行性和科学有效性，2种方法评价结果的具体对比，见表5。

表5 2006—2016年郑州市供水安全预警指标数据Table 5 Water supply safety early warning indicators for Zhengzhou city from 2006 to 2016

基于直觉模糊集理论的评价结果与采用物元可拓法的评价结果总体接近，其中2010年出现一定的偏差，从相关资料得知,这是因为郑州市政府成立的节水部门提高了居民的节水意识，使得用水状况在2010年出现明显好转，人均日生活用水量(C1)低于其他年份使得供水安全预警等级下降。其后水质达标率(A3)及其他指标逐渐优化使得供水安全预警等级下降，并基本保持在无警等级，城市供水处于安全状态。2010-2012年在权重较高的几类指标上表现良好，使得供水安全性略高于物元可拓法的评价，从整体分析来看直觉模糊集理论评价结果总体接近物元可拓法的评价，表明直觉模糊集理论评价结果较为可靠，应用效果比较好，具有实用性和借鉴性。

2.3 评价指标的灵敏度分析

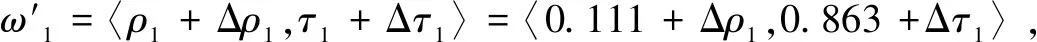
借助MATLAB编程求解不等式组，可以得到Δρ1和Δτ1的可行域，如图1所示，图中阴影部分表示满足不等式组的所有可行解。阴影部分的面积在整个区域中的比重越大，说明该指标敏感性越弱，灵敏度低，其权重的变化对评价结果的影响越小。

图1 指标A1权重敏感性分析Fig.1 Sensitivity analysis of index A1 weight

限于篇幅，以此类推。本文仅对指标B1与C1进行计算，其中，可行域如图2～3所示，其结果如下。

图2 指标B1权重敏感性分析Fig.2 Sensitivity analysis of index B1 weight

图3 指标C1权重敏感性分析Fig.3 Sensitivity analysis of index C1 weight

经计算，图1阴影面积为0.098 61，图2阴影面积为0.386 54，图3阴影面积为0.018 33，图2中阴影部分的面积最大，因此在本文选取的3个指标中，指标B1的敏感性最弱，其指标的权重变化对城市供水安全预警评价结果影响最小。通过对指标敏感性的分析可以发现指标敏感性与指标权重无关，因此可以将指标敏感性作为确定指标权重的重要考量标准。当指标敏感性越强，指标权重的变化对供水安全预警评价结果影响越大，指标权重轻微的变化就可能导致评价结果有相对大的变化，则确定该指标的权重时需要仔细考虑，多方求证，最大程度的保证权重的准确。反之指标敏感性较弱，可适当减少确定权重的工作量。这对于提高评价结果的准确性是十分有利的。

3 结论

1)综合考虑主客观权重，避免单一权重的局限性，按照直觉模糊集理论模糊确定出权重的范围，避免了确定具体权重数值的缺陷，使得评价结果更加灵活可信。

2)对指标A1，B1与C1进行权重的敏感性分析，C1敏感性高于A1高于B1，指标B1的敏感性最弱，其指标的权重变化对城市供水安全预警评价结果影响最小。敏感性分析有利于指导权重的确定，提高评价结果的准确性。

3)通过算例对比表明，直觉模糊集方法评价城市供水安全预警等级具有可行性、合理性、可靠性，可以作为城市供水安全预警等级评价的一种方法。