火星轨道交会自主导航与制导方法

刘 涛，解永春，王晓磊，胡锦昌

(1.北京控制工程研究所,北京 100190; 2.空间智能控制技术国家级重点试验室,北京 100190)

0 引 言

人类从20世纪60年代即开始对火星进行探测，逐步实现了掠过式观测、环绕火星探测、在火星着陆进行现场巡视探测。人类对火星的探测下一阶段将是采样返回(Mars sample return,MSR) 任务。实现MSR任务的一种可行方案为：火星探测器包括轨返组合体和着陆上升组合体2部分。轨返组合体在火星轨道上等待，着陆上升组合体完成采样后由上升器携带样品入轨，轨返组合体与上升器完成交会对接和样品转移，然后轨返组合体返回地球[1-2]。火星轨道交会对接技术是实施MSR的关键技术。从火星动力上升需要耗费大量燃料，上升器规模非常有限，系统配置必须简单，上升器很难具备自主定轨能力，且入轨偏差会较大。这需要轨道返回组合体具备自主确定自身轨道和上升器轨道，并完成椭圆轨道交会对接的能力。

在火星环绕段，探测器能够采用可见光自主导航敏感器捕获到清晰的火星图像；此外，火星属于类地球行星，其大气层主要成分是二氧化碳，火星大气层温度与太空有明显的温度梯度，通过红外探测同样可以确定火星的边缘。获得火星图像后，采用图像处理中的边缘检测与提取算法完成火星轮廓提取，计算包括火星视半径和火星中心在内的观测信息；同时，为完成交会任务，轨返组合体需要配备相对敏感器，可测量两航天器间的相对位置。综合光学自主导航敏感器和相对敏感器的观测信息，通过设计导航滤波器可同时估计得到两航天器的轨道。在光学自主导航敏感器导航系统设计中，行星中心的图像提取是关键环节，主要方法包括重心法和拟合法。重心法的有效性取决于目标能量分布的均匀性，边缘的完整性和边缘特征的提取准确性[3]。拟合法主要利用的是提取行星边缘的特征[4]。文献[5-6]针对可采用三维椭球建模近似描述的天体，研究了成像椭圆匹配和中心提取算法，以得到天体质心和视半径。吴双卿等[7]用otsu最大类间方差法自动分割，提取边缘闭区域轮廓，并用有效轮廓数据进行椭圆拟合计算出目标中心象素位置以获得视线角信息。而吴功友等[8]提出了利用探测器上的光学照相机跟踪火星中心以提高地面无线电定轨预报精度。在相对敏感器研制方面，人类从20世纪60年代开始实施空间交会对接，已研制出多种不同体制不同作用范围的相对测量敏感器，包括：微波雷达、激光雷达、RGPS、成像式交会对接敏感器、可见光/红外捕获相机等。其可提供的观测量包括：相对距离和视线角，或直接输出相对位置，近距离还可输出相对姿态[9]。

在制导方法方面，目前可用于近程交会段的交会制导律主要包括：基于绝对轨道参数的LAMBERT制导，和基于相对轨道参数的C-W制导、视线制导以及T-H制导等，其中LAMBERT制导和T-H制导可用于椭圆轨道交会。美国20世纪所进行的Apollo工程和航天飞机任务均采用LAMBERT制导进行交会轨道控制[10-11]，LAMBERT制导基于航天器绝对轨道参数进行设计，求解较为复杂但可兼顾远程交会和近程交会轨控；T-H制导是一种基于椭圆轨道近距离线性化相对动力学模型的制导律，其计算量较C-W制导大[12]。目前，还没有T-H制导在轨实际应用的报道，但其计算量显著小于LAMBERT制导，而在相对距离较近且转移时间较短时，其精度与LAMBERT制导相当，因此具有良好的应用前景。

目前，有关火星轨道交会技术的研究还比较少。Sotto等[11]以欧空局Aurora计划为背景，讨论了火星椭圆轨道交会对接的实施策略，给出了5 km以内的交会方案，但未就具体的导航和制导技术进行讨论。Pelletier等[14]针对火星近圆轨道交会任务，基于激光雷达测量，设计了相对导航滤波器用于1 km以内的交会控制。还未见文献对火星椭圆轨道近程交会的导航和制导技术进行系统分析，本文以火星采样返回任务为背景，对火星轨道交会自主导航和制导技术进行研究。采用光学自主导航敏感器测量的火心方向和视半径，相对敏感器测量的相对位置等信息，通过设计滤波器同时估计上升器和轨返组合体的轨道。由于涉及图像处理算法，光学自主导航敏感器的更新频率较低。为此，在滤波器设计中，设计了一种连续测量构造方法，确保每个滤波周期均可进行测量更新，以提高导航精度。基于导航估计结果，采用T-H制导设计了4脉冲共椭圆交会策略，从而构成火星轨道近程交会自主导航和制导方案用于完成交会任务。

论文中对矢量通过上标标识对应坐标系中的坐标，如ri,ro,rb分别表示惯性系、轨道系、本体系下的坐标，而通过下标标识具体物理含义。

1 导航滤波器

设定轨返组合体安装有光学自主导航敏感器，并配有激光雷达用于相距数十千米以内的相对测量。光学自主导航敏感器获得的火星图像经图像信息处理后，输出火心方向与火心距；激光雷达可以输出相对距离ρ以及视线仰角α和方位角β，据此得到上升器相对轨返组合体的位置。依据相关敏感器的性能，本文分析所采用的敏感器测量性能见表1。

自主导航系统原理框图如图1所示。采用EKF设计导航滤波器，滤波周期选择为Δt=200 ms(5 Hz)。利用轨道动力学方程对航天器轨道进行外推；由于光学自主导航敏感器的更新频率远低于滤波计算频率，为此依据最近时刻导航敏感器的输出，采用观测量连续化算法构造当前时刻的轨返组合体位置，并与激光雷达所测的相对位置构成总观测量；利用EKF给出对轨道外推的修正量，得到两航天器轨道的最优估计值。

表1 敏感器测量性能(3σ)Table 1 Measurement capability of sensors(3σ)

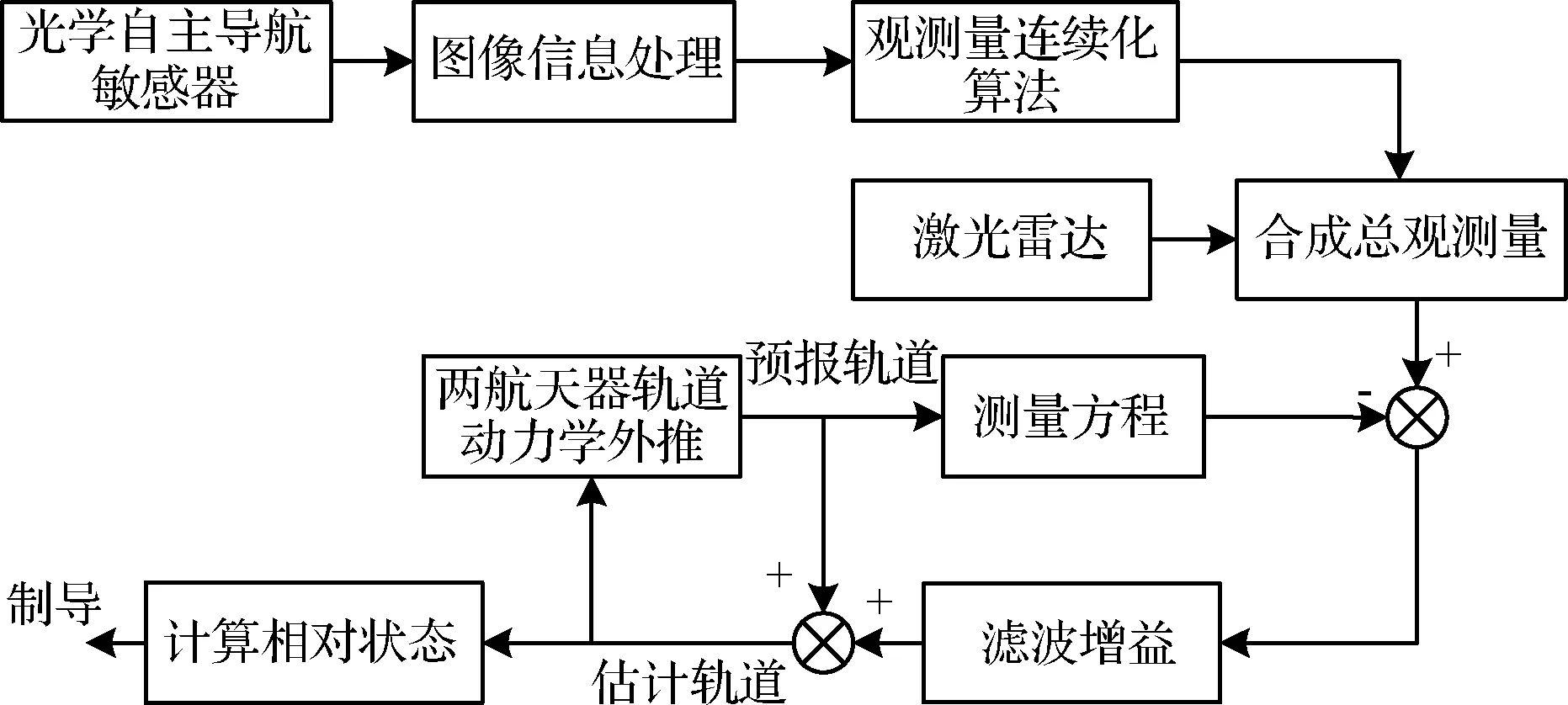
图1 自主导航原理框图Fig.1 Flowchart of autonomous navigation algorithm

1)状态预估

(1)

(2)

(3)

其中，

Fj(Xj)=

Fj的具体形式见文献[15]。再以滤波周期Δt得到离散化干扰方程：

(4)

(5)

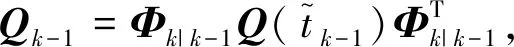
2)观测量连续化算法

(6)

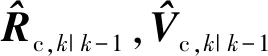
(7)

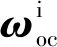
(8)

(9)

(10)

3)总观测量

4)测量方程

光学自主导航敏感器的观测量为火心方向和视半径，结合惯性定姿结果，可以得到惯性系中的火心方向和火心距，对应的测量方程记为h1(Xk)。激光雷达的直接观测量为相对距离和视线角，利用定姿结果，可以得到惯性系中的相对位置，对应的测量方程记为h2(Xk)。总测量方程列写为

(11)

其中，vdir,k为火心方向测量噪声，vρ,k为火心距测量噪声，vrel,k为相对位置测量噪声。测量噪声均值为0，方差依据敏感器性能设置，见表1。

对测量方程进行线性化

(12)

式中：

5)计算相对状态

(13)

(14)

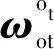
2 交会制导律

为完成交会，需要依据导航结果，采用制导律进行交会轨道控制。以下给出T-H制导的具体计算。

轨道坐标系OoXYZ的定义：其原点Oo为航天器的质心，OoX轴为位置方向且背离火心，OoZ轴指向轨道角速度方向，OoY轴与OoZ，OoX轴构成右手系。

依据二体轨道得到相对动力学模型描述为

(15)

将式(15)在目标航天器轨道系中展开，并对引力加速度差采用Taylor分解且仅保留一阶项：

(16)

其中，θt为目标航天器的真近点角。式(16)为线性时变方程，求取状态转移矩阵并没有统一的方法。Tschauner和Hempel给出了偏近点角表示的解析解，称为T-H方程。Carter用目标轨道真近点角表示得到了相对运动方程[17]，为T-H的应用奠定了基础。以目标器轨道真近点角为自变量，则有

(17)

代入式(16)可得：

(18)

其中，γ=1+etcosθt。

X=ΦTH(θt)d

(19)

展开后有

(20)

(21)

式中：

0.5etsinE0cosE0)

采用状态转移方程得到任意时刻的相对状态与初始状态间的关系为

X(θt)=ΦTH(θt,θt 0)X(θt 0)

(22)

(23)

进而可得t0需要施加的速度增量为

(24)

式(23)和式(24)中的相关参数均采用导航值计算得到。

3 近程交会策略

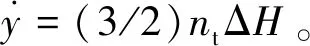
形成“共椭圆轨道”后， Apollo计划中采用了共椭圆视线推力逼近策略进行近程交会段的制导设计[19]。共椭圆视线推力逼近策略中，追踪航天器从目标航天器后下方进入飞向目标器的转移轨道，并与目标航天器逼近，其终段起始位置(TPI)点处的视线角(即仰角)αTPI刚好是TPI处制导脉冲的速度增量方向，若追踪航天始终保持目标指向姿态，则执行该制导脉冲时无需进行调姿机动，进而避免相对测量敏感器丢失目标。Apollo计划中，TPI处的视线角设定为αTPI=27.5°，制导转移时间对应目标航天器所掠过的轨道幅角约为130°，此即对应飞行转移时间ttran[20]。

由于共椭圆视线推力逼近策略转移时间较短且进程稳健，所以本文采用共椭圆视线推力逼近作为火星椭圆轨道近程交会段的交会策略，并将近程交会的瞄准位置直接设定为上升器。近程交会制导方案设计采用四脉冲T-H制导，其中第4脉冲为制动脉冲，第2和第3脉冲为中间修正脉冲，临近脉冲间的时间间隔相等，首末脉冲间的转移时间对应上升器所掠过的轨道幅角约为130°。

4 数值仿真

采用Monte Carlo数值仿真对所设计的近程交会自主导航和制导方法性能进行校验。

1)仿真设置

在历元J2000.火星天球坐标系中定义轨道，并考虑20阶火星非球形摄动。依据共椭圆轨道的特性独立设置200组初始轨道(设置方式见表2)。采用刚体转动方程描述航天器姿态运动；轨返组合体三轴采用2台100 N发动机实施轨控，三轴姿态采用2×25 N发动机以力偶形式实施控制。仿真中忽略定姿误差，加速度计测量误差。敏感器测量值误差依据表1设置。

2)导航滤波器性能分析

表2 初始轨道参数设置Table 2 Initial orbit parameters set

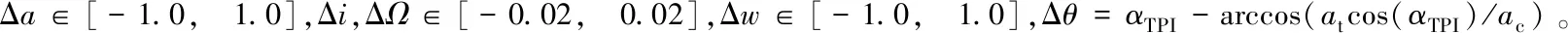
导航滤波器对两航天器轨道的估计精度相当，其中位置误差小于1000 m，速度误差小于3 m/s；相对位置误差小于40 m，速度误差优于0.1 m/s，其中y方向(接近方向)的位置估计误差大于其他两轴。这主要是由于光学自主导航敏感器更新频率低，虽然采用了观测量连续化计算，测量时延仍会造成相对位置估计系统偏差。

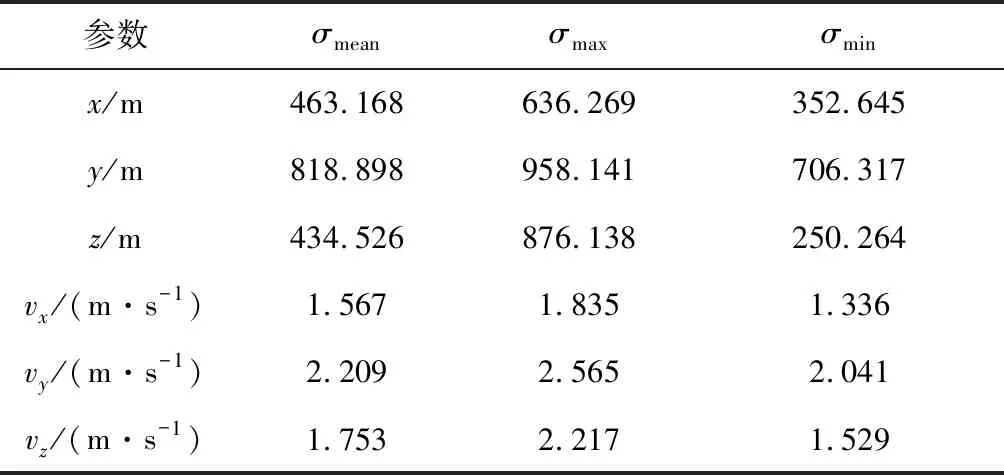
表3 轨返组合体轨道估计误差Table 3 Orbit states estimation error of orbit vehicle

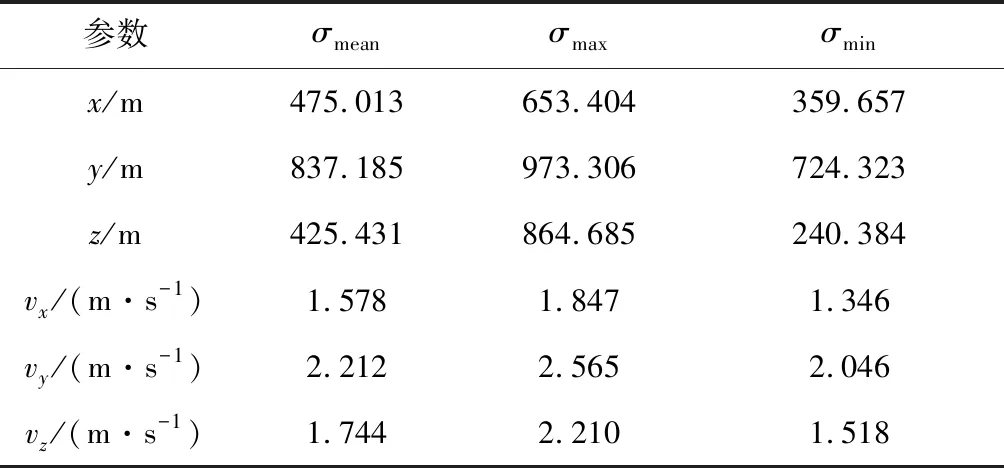
表4 上升器轨道估计误差Table 4 Orbit states estimation error of ascend vehicle

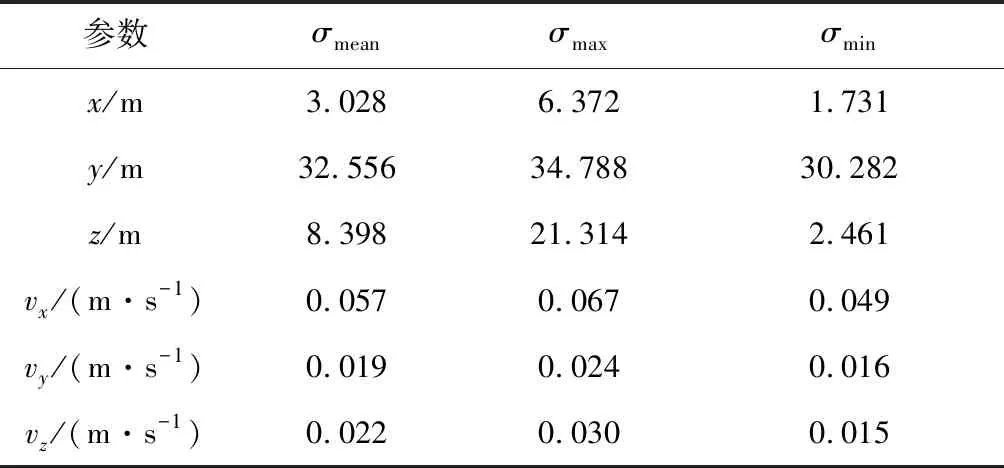
表5 相对运动状态估计误差Table 5 Relative states estimation error

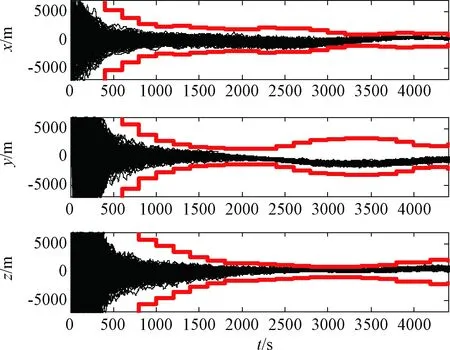
图2 轨返组合体位置估计误差Fig.2 Position estimation error of orbit vehicle

图3 轨返组合体速度估计误差Fig.3 Velocity estimation error of orbit vehicle

图4 上升器位置估计误差Fig.4 Position estimation error of ascend vehicle

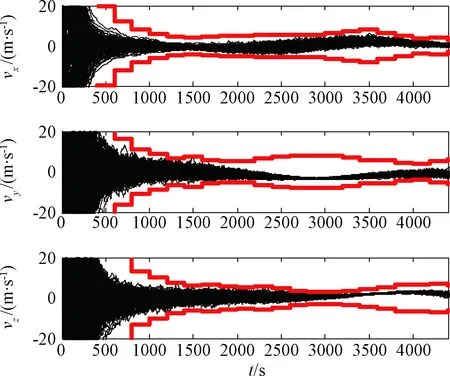
图5 上升器速度估计误差Fig.5 Velocity estimation error of ascend vehicle

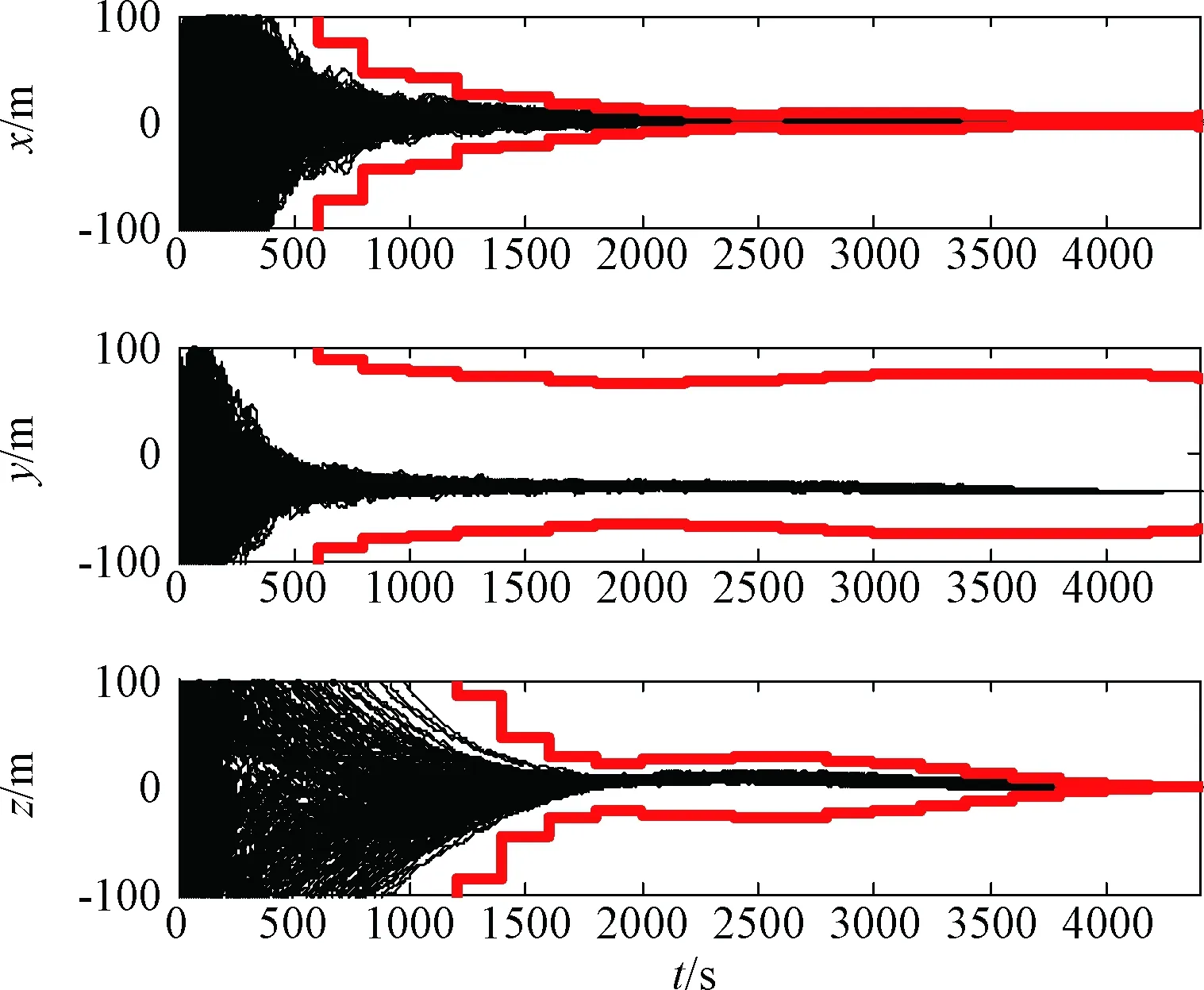
图6 相对位置估计误差Fig.6 Relative position estimation error

图7 相对速度估计误差Fig.7 Relative velocity estimation error

3)制导性能分析

制导结果见表6～7和图8。近程交会末端相对位置误差最大不超过200 m。实际飞行任务中，通常将近程交会细分为寻的段和接近段以及平移靠拢段[21]，仿真分析的阶段相当于寻的段。寻的段的交会目标是捕获目标航天器轨道系中的停泊点，从工程设计的角度，200 m的制导误差完全满足捕获停泊点的要求。由表7可知近程制导最大速度增量不超过12 m/s。综上，所设计的交会导航和制导策略可完成近程交会任务，制导精度较高且燃料消耗不大。

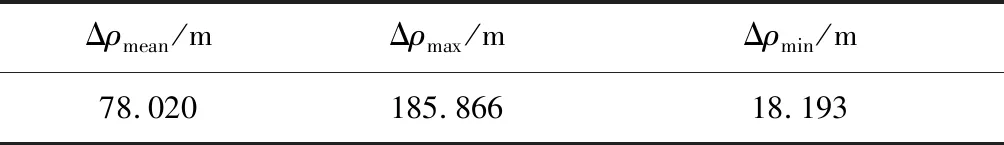
表6 近程交会末端相对位置误差Table 6 Terminal relative position error of RVD

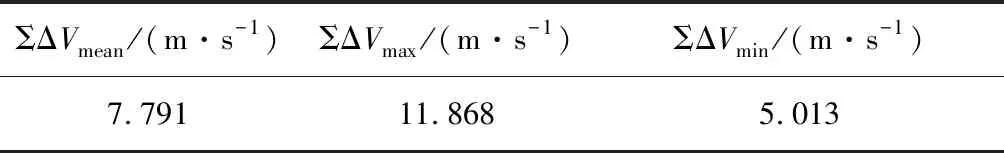
表7 近程交会制导速度增量Table 7 Total velocity increment of guidance impulses

图8 近程交会末端相对位置Fig.8 Relative position results of RVD

5 结 论

进行火星采样返回将是人类深入探测火星的技术发展方向，而火星轨道交会对接是完成采样返回任务的关键技术。本文以火星采样返回任务为背景，对火星轨道交会自主导航和制导技术进行了研究。采用光学自主导航敏感器测量的火心方向和视半径，相对敏感器测量的相对位置等信息，通过设计滤波器同时估计上升器和轨返组合体的轨道。在滤波器设计中，针对光学自主导航敏感器更新频率低导致导航精度不高的问题，设计了连续观测量构造方法，从而确保每个滤波周期均可进行测量更新，以提高导航精度。基于导航估计结果，采用T-H制导设计4脉冲共椭圆策略完成近程交会轨道控制。采用Monte Carlo数值仿真全面校验了所提出的火星轨道近程交会自主导航和制导方法的有效性。所提出的方法为火星采样返回工程设计提供了参考。