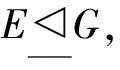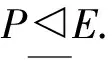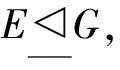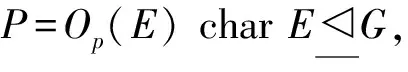几乎M-可补子群对两类拟F-群结构的影响

高百俊，王克科

(1.伊犁师范大学 数学与统计分院，新疆 伊宁 835000；2.扬州大学 数学科学学院， 江苏 扬州 225002)

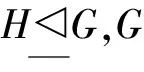
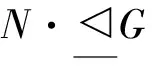
文献[2]通过对有限群的F-离中心主因子上自同构的限制，提出拟F-群的概念，并研究了拟超可解群和p-拟超可解群[3].结合M-可补子群[4]和几乎s-正规子群[5]两种子群的性质，文献[6]给出了几乎M-可补子群的定义，并利用Sylow 子群的极大子群的几乎M-可补性，对p-幂零群、超可解群等饱和群系进行了研究.目前，相关学者利用子群的几乎M-可补性研究饱和群系已取得了一些成果[7-9]，但是关于拟F-群可解饱和群系的研究结果却很少.由于p-超可解群类包含于p-拟超可解群类、超可解群类包含于拟超可解群类，作为饱和群系向可解饱和群系的延伸，论文将继续利用Sylow 子群的极大子群的几乎M-可补性，对p-拟超可解群和拟超可解群这两类可解饱和群系的结构进行探究.

1 预备知识

引理1[7]设G是有限群，有

(1) 若H≤K≤G，且H在G中几乎M-可补，则H在K中几乎M-可补；

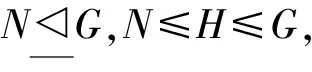
(3) 设π是一个素数集，K是G的正规π′-子群，且H是G的π-子群，若H在G中几乎M-可补，则HK/K在G/K中几乎M-可补；

引理2[7]设G是有限群，P是G的一个Sylowp-子群，p是G的极小素因子.G是p-幂零的当且仅当P的任意极大子群在G中要么有p-幂零补，要么有几乎M-补.

引理3[5]设p∈π(G)，P是群G的一个p-子群且在G中有一个M-补子群B，则

P∩B=P1∩B=Φ(P)∩B，

且|G:P1B|=p，P1是P的任意极大子群.

引理4[10]设P是一个初等交换p-群且|P|=pd，d≥2,p是一个素数，且

Md(P)={M1,…,Md，

有

(a)Xi=∩i≠jMj是p阶循环群；

(b)P=.

引理5[2]若F是一个包含幂零群类的饱和群系，则拟F-群类(p-拟F-群类)是可解饱和群系且拟F-群(p-拟F-群)的正规子群也是一个拟F-群(p-拟F-群).

引理6[11]设G是有限群，N为G的子群，有

(2)F*(F*(G))=F*(G)≥F(G)；如果F*(G)可解，则F*(G)=F(G).

(3) 如果K≤Z(G)，则F*(G/K)=F*(G)/K.

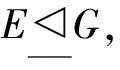
2 主要结论

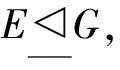
证明假设结论不真，设(G,E)是使|G||E|最小的极小阶反例.

(1)Op′(E)=1.事实上，若K=Op′(E)≠1，考虑商群G/K，由引理1(3)知(G/K,E/K)满足定理的条件，从而由(G,E)的选择可得G/K是p-拟超可解群，故G是p-拟超可解群，矛盾.

(2)E=P.若E=G，则由引理2得E是p-幂零的，又由(1)可知E=G=P.若E

(3) 若L是G的任意一个包含于E的极小正规子群，则L≠P.否则，由引理1(4)得|L|=p.又由(2)及已知得G/L=G/E是p-拟超可解群，所以G也是p-拟超可解群，矛盾.

考虑

P∩PiK=Pi(P∩K)，

则必有P∩K

Pj(P∩K)=P.

由于Pj在PjK中是M-可补的，由引理3，有

Pj∩K=Φ(Pj)∩K=1，

即

|P|=|Pj||P∩K|，

即|P∩K|=p.

考虑(G/(P∩K),E/(P∩K))，由引理1(2)和(G,E)的选择，可得G/(P∩K)是p-拟超可解群，故G也是p-拟超可解群，矛盾.因此∀Pi<·P，都有P∩K≤Pi，从而，有

P∩K≤Φ(P)=1，

即

以上结论是借助群阶的极小素因子，利用几乎M-可补子群的性质对p-拟超可解群的结构进行了研究.接下来，将从群扩张的角度来考查几乎M-可补子群对拟超可解群的影响.

证明假设结论不真，设(G,E)是使|G||E|最小的极小阶反例.

考虑

P∩PiK=Pi(P∩K)，

易见P∩K

从而，有

P∩K≤Φ(P)=1，

即

证明假设结论不真，设(G,E)是使|G||E|最小的极小阶反例.

(1)F*(E)=F(E)≠E.由文献[7]中定理3.3.6可知F*(E)是超可解的，又由引理6(2)得F*(E)=F(E)，最后，由定理2知F*(E)=F(E)≠E.

(2) 存在p∈π(F*(E))，使得P是F*(E)的非循环Sylowp-子群且P=Op(E).如果F*(E)的每个Sylow 子群都是循环群，那么由引理7可知E的每个G-主因子都是循环的，因此E≤ZU(G).又G/E是拟超可解群，故G是拟超可解群，矛盾.

F*(E)=F(E)≤CE(L)，L≤Z(CE(L))，

所以由引理6(1)和(3)，有

F*(CE(L)/L)=F*(CE(L))/L=F*(E)/L.

由引理1(2)及(G,E)的选择，得G/L是拟超可解群，故G也是拟超可解群，矛盾.

考虑

P∩PiB=Pi(P∩B)，

易见P∩B

由引理4可知P的每一个极小子群在G中均正规，这与(3)矛盾. 于是∃Pj<·P，使得P∩B≤Pj，于是Pj(P∩B)=P. 因为Pj在PjB中是M-可补的，由引理3，得

Pj∩B=Φ(Pj)∩B=1，

|P|=|Pj||P∩B|，