一类拟周期非线性哈密顿系统的约化性

李 佳，朱春鹏

(徐州工程学院 数学与物理科学学院, 江苏 徐州 221111)

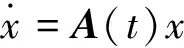
受文献[4-5]的启发,论文把文献[5]的结果推广到矩阵A可以有重特征值但并不要求A能够对角化的情况.

定义1如果f(t)=F(ω1t,ω2t,…,ωrt)， 其中F(θ1,θ2,…,θr)所有变量都是2π周期的，且θi=ωit，i=1,2,…,r，则称函数f是频率为ω=(ω1,ω2,…,ωr)的拟周期函数.

如果F(θ)，θ=(θ1,θ2,…,θr)在Dρ={θ∈Cr||Imθi|≤ρ,i=1,2,…,r}上解析,则称f(t)在Dρ上是解析拟周期的.记f(t)在Dρ上的最大值范数为

定义2如果所有的qij(t)(i,j=1,2,…,n)在Dρ上是解析拟周期的,则称矩阵函数Q(t)=(qij(t))1≤i,j≤n在Dρ上是解析拟周期的.

定义Q的范数

||Q||ρ=n×max1≤i,j≤n||qij||ρ，

则

||Q1Q2||ρ≤||Q1||ρ||Q2||ρ.

为了简单起见,如果Q是一常数矩阵,记||Q||=||Q||ρ.Q的平均记为

[Q]=([qij])1≤i,j≤n，

1 主要定理及相关假设

定理考虑非线性哈密顿系统

(1)

假设A可以有重特征值λi,λi≠0，i=1,2,…,2n. 假设Q(t,ε),g(t,ε),h(x,t,ε)在Dρ上是频率为ω=(ω1,ω2,…,ωr)的解析拟周期矩阵，并且关于ε解析.此外，h(x,t,ε)在Ba(0)上关于x是解析的，h(0,t,ε)=0，Dxh(0,t,ε)=0，其中Ba(0)是中心在原点、半径为a的球，ε∈(0,ε0)是参数.

假设1(非共振条件)λ=(λ1,λ2,…,λn)和ω=(ω1,ω2,…,ωr) 满足

(2)

(3)

其中:k∈Zr{0}，τ>r-1，α>0是一个小常数.

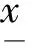
其中:k1≠k2，k,k1,k2=1,2,…,2n,ε∈(0,ε0),δ,δ1,δ2是常数.

假设3||Dxxh(x,t,ε)||≤K， 其中x∈Ba(0)，ε∈(0,ε0).

则存在一个具有正Lebesgue测度的Cantor集E*⊂(0,ε0)，使得当ε∈E*时, 存在一个拟周期辛变换x=ψ(t,ε)+φ(t,ε)y，其中ψ(t,ε) 和φ(t,ε)是频率为ω的解析拟周期矩阵, 使得 (1) 式变为哈密顿系统

(4)

其中:B(ε)是常数矩阵,h∞(y,t,ε)=O(y2),y→0. 此时，meas((0,ε0)E*)=o(ε0)，当ε0→0.

注1一般来说,Q,g,h都依赖于ε. 下面为了简单起见，有时省略其中的参数ε.

注2子集E*⊂(0,ε0)是一个Cantor集. 于是，函数在E*上关于ε的光滑性理解为Whitney光滑. 具体见文献[11].

2 定理的证明

事实上，论文重特征值但并不要求A能够对角化的情况，可参考文献[5]中的第一步KAM(Kolmogorov-Arnold-Moser theorem)步骤.因此，首先给出第一步KAM步骤，而以后的KAM迭代变为不同特征值的情况，完全类似文献[5].

首先，在第一步KAM步骤中，对于(1)式，通过做一个辛变换，使得εg(t)中的ε的次数变为ε2.

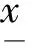
(5)

其中

解方程

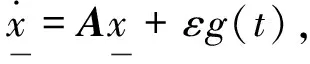
(6)

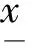
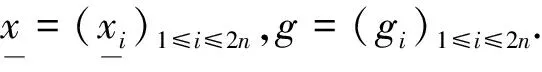
比较方程(6)两边的Fourier系数，则方程(6)变为

(7)

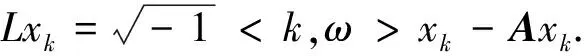
Lxk=εgk.

(8)

(9)

对于哈密顿系统(5)，做辛变换y=eεP0x1，其中哈密顿矩阵P0满足

得到哈密顿系统

(10)

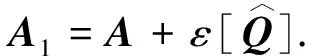
第一步以后的KAM步骤、KAM迭代的收敛性以及测度估计的证明完全类似于文献[5]，此略.