多定位源数据分析的特征向量空间滤波模型及仿真实验

姚海云，舒红，汪善华，曾坤

(1.武汉大学测绘遥感信息工程国家重点实验室，湖北 武汉 430079； 2. 深圳市地籍测绘大队，广东 深圳 518034；3.武汉益士天慧科技有限公司，湖北 武汉 430000)

1 引 言

由于障碍物遮挡、墙壁阻隔和多路径效应等因素存在以及室内环境极为复杂，全球卫星定位系统无法实现室内精确定位。近年来，随着近距离无线通信和移动网络技术发展，基于位置的服务(LBS)越来越受到重视[1]。根据美国环境保护局报告统计，人们有近70% ～ 90%的时间是在室内度过[2]。为了克服卫星定位缺陷并实现在室内环境中的精确定位，国内外研究人员在室内定位中引入了红外传播、WLAN、超声波、射频识别(RFID)、低功耗蓝牙、紫蜂(ZigBee)、无线传感器网络(WSNs)等多种技术[3]，但是以上技术多数要布设相应定位设备方可展开定位工作。室内定位源合理布设对于最终的定位精度存在很大的影响。文献[4]将评价卫星空间几何布局结构的定位精度影响的PDOP指标借鉴到UWB技术室内定位中，仿真PDOP值研究了室内定位测站布设的定位精度影响，结论是合理位置的测站布设会降低环境对信号的干扰，提高定位精度。本文通过特征向量空间滤波模型分离表达定位源结果的空间自相关获得更为可靠的定位结果。为了更方便表征定位源的空间布局，仿真的定位源是发射定位源，即需要布设相应测站的定位源，仿真情景参考现实场景，如应用UWB、Wi-Fi、LED、超声波、蓝牙等一系列定位源定位时均需要布设测站。

1970年，美国地理学家W.R.Tobler提出了“地理学第一定律(Everything is related to everything else，but near things are more related than distant things)”[5]，指导着自然地理和人文地理的观测数据分析。室内定位中，众多定位源结果可以看作是多个相关随机变量的一次实现。同样，众多定位源存在一定的空间布局及空间结构效应，可以统计解释为定位源结果的空间自相关。空间自相关会导致不同定位源影响系数(回归系数)的方差膨胀效应，方差膨胀导致参数估值的不确定性被低估[6]，导致回归模型正确性检验不显著，定位粗差的误判性也将大大增加。从定位系统功能角度，定位粗差可近似解译为系统故障。Griffith(2000，2003)、Tiefelsdorf和Griffith(2007)提出了特征向量空间滤波方法，空间滤波的基本思想是通过对空间邻接矩阵进行特征向量分解，从中提取一组特征向量作为解释变量或空间结构代理变量加入模型中，这样可以保证回归模型满足空间独立性前提假设(非空间自相关假设)[7，8]。该方法最大的优势在于利用这些代理变量有助于空间数据空间自相关性识别并分离开来，使得空间结构效应分离后的随机变量间是彼此独立的，再使用传统回归模型来分析数据。空间滤波的思想来源于时间序列滤波的思想，通过不同手段来分离表征时间或空间自相关性。空间统计及空间计量经济学中，空间滤波(Spatial Filtering)可以看作地理数据稳健统计方法，构造的数理算子用于将空间结构效应(正向结构信息或负向冗余影响)、趋势和噪声从信号中逐一分离出来，最终获得更加自然更加准确的统计推断结果[8]。

本文设定一种定位源布设，在此基础上展开研究。通过空间邻接矩阵来表达定位源的空间布局，对空间邻接矩阵进行特征向量的分解，运用特征向量空间滤波模型来分离定位源空间自相关。仿真结果表明，通过特征向量空间滤波模型，使得用户定位结果和回归系数的估值得到了明显的提高。本文研究为定位源空间自相关的分离表达提供了一种简便可行的方法。

2 多定位源空间邻接矩阵与特征向量空间滤波模型

2.1 定位源空间邻接矩阵

空间邻接矩阵(Spatial Adjacency Matrix，SAM)直接表达了定位源之间的邻接关系或空间布局。同时，空间邻接的确定也是度量空间相关性的基础，犹如集合邻域定义作为拓扑模型的基础。基于定位源两两可见(无信号传输遮挡)来定义定位源空间邻接矩阵。定位源之间可见，则认为它们是空间邻接(直接邻接或一阶邻接)，设置权重值为1，反之，权重值为0。具体的表达式为：

(1)

其中，i和j是不同的定位源，假设有n个定位源，则空间邻接矩阵W是n×n阶。这里，假设场景存在12个定位源，一种定位源布局如图1所示，图中带有双向箭头的线段表示定位源是互相可见的。由定位源布局图以及式(1)进而可以给出多定位源邻接矩阵如表1所示：

图1 室内定位定位源布局示意图

定位源邻接矩阵 表1

由表1可知，定位源网络是一个无向图，SAM是对称方阵。

2.2 特征向量空间滤波模型

特征向量空间滤波模型使用了一组特征向量合成的代理变量，特征向量通过表达多定位源空间结构关系的n×n空间邻接矩阵W分解获得，这些代理变量表征并分离了定位源数据空间相关性。代理或控制变量加入一个传统设定模型(线性回归模型)，就可以用于具有空间结构的多定位源变量或观测变量的数据融合分析。

空间统计中，存在两种空间自相关性建模方式：①空间滤波中空间代理变量的回归系数；②空间自回归中Moran系数。空间滤波中，空间结构代理变量直接来自邻接矩阵的特征向量分解。自然地，表达空间自相关性的这两种方法存在内在联系。

给出n×n空间权重矩阵W，取值为0和1，则随机变量y的空间自相关度量可以用Moran系数表示：

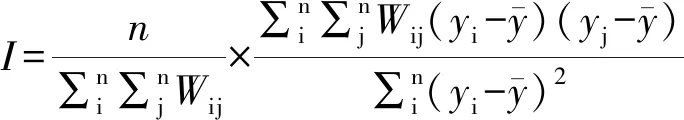
(2)

写成矩阵形式可表示为：

(3)

(4)

进而可解得n个特征值λ=λ1，λ2，…，λn，亦可通过(W*-λI)E=0解得特征向量E，每个特征值λj都有一组对应的特征向量Eij=E1j，E2j，…，Enj，这些特征向量的均值为0，并且互为正交。对于每个独特的空间组合，Moran系数由对应的特征值决定：

(5)

3 多定位源数据融合的统计模型及仿真分析

3.1 多定位源数据融合模型

多个定位源协同工作时，单个定位源融合以得到精度更高的用户定位结果。我们研究应用特征向量空间滤波分离表达不同定位源空间自相关，暂且没有给定不同类型定位源的具体观测方程，这里将多元线性回归模型作为定位源数据融合模型。通常，Wi-Fi指纹匹配定位和LED等定位方式下，观测方程均为线性观测方程。再者，一般非线性化观测方程可进行线性化观测方程。所以这里的定位源数据融合模型采用多元线性回归模型。

假设场景存在6个定位源正常工作，分别记为X1，X2，X3，X4，X5，X6，最终的多定位源数据融合的统计模型如下表示：

Y=β1X1+β2X2+β3X3+β4X4+β5X5+β6X6+ε

(6)

其中，ε表示扰动项，假设扰动项为服从独立同分布的高斯变量，Y表示最终融合的用户定位结果。

在上述模型中加入空间代理变量后，模型结构调整为：

Y=β1X1+β2X2+β3X3+β4X4+β5X5+β6X6

(7)

其中，空间代理变量Eq是从W*中提取的向量，γq是空间效应系数。关于n维定位源向量中提取有代表性的特征向量作为空间代理项，Griffith(2009)给出了一种经验方案，即从所有的特征向量中提取一组特征值大于某一阈值的候选特征向量，该阈值满足下列Moran系数条件式(8)：

I/Imax>0.25

(8)

上式中I是通过式(5)求出的Moran系数，Imax为Moran系数最大值。

3.2 特定空间布局的多定位源仿真数据生成

正如引言中提到的，定位源结果是存在一定空间自相关的。所以在本文研究中，实验数据采用高斯分布空间自相关随机变量的计算机抽样随机数。由于高斯分布具有线性变换下保持分布规律不变的性质，因此多维相关高斯分布随机数可以通过协方差矩阵的Cholesky因子对独立高斯分布随机变量抽样序列进行线性变换来产生[9～14]。令每个变量Xi(i=1，2，…，n) 均为m个随机数序列构成的列向量，Xm×n=(X1，X2，…，Xn)为需要产生的n维统计相关的高斯分布随机变量抽样序列，其均值为μ=(μ1，μ2，…，μn)，协方差矩阵为：

(9)

则产生随机变量X的n维相关高斯分布的随机数步骤如下：

(1)产生n维独立标准高斯分布随机变量随机数，Ym×n=(Y1，Y2，…，Yn)，每个序列的随机变量随机数个数为m；

(3)进行线性变换，令：

Xm×n=Ym×n·Cv+μm×n

(10)

即可生成n维相关高斯分布随机变量Xm×n=(X1，X2，…，Xn)抽样序列。

4 室内定位多源数据融合的场景仿真分析

相对于室外定位，比如在大型商场、电影院、展馆、机场等室内环境相当复杂，外界干扰无法控制。运用仿真分析方法可控制上述无法预测的环境干扰，实现局部环节技术的针对性研究。因而，本文研究场景采用仿真的方式实现，定位源布局采用2.1中的解决方案。

4.1 多元线性回归模型仿真

根据3.2章节内容生成实验数据，假设场景有6个定位源工作，假设它们定位结果均值分别为 0.8 m、1.7 m、1.0 m、0.5 m、1.6 m、0.7 m，定位源融合后均值为 1.0 m。协方差矩阵为设定的满足对称正定7×7矩阵。令式(10)中的m=12，n=7，将X12×7矩阵中的第7列作为多定位源数据融合结果，X12×7矩阵中的第1～第6列作为各个定位源结果。生成的这些数据均为高斯分布相关随机变量的样本，对其应用多元线性回归分析，显著性水平α=0.01，得到结果如表2所示：

传统多元线性回归模型估计结果 表2

表2中，R2表示判定系数，R2越接近1说明回归方程越显著；F表示统计量，F值越大，说明回归方程越显著，p值越小说明模型参数越显著，RMSE表示多定位源数据融合结果的中误差。

4.2 特征向量空间滤波模型仿真

在4.1的基础上，在一般多元线性回归变量中根据式(8)加入空间代理变量，再次进行特征向量空间滤波模型ESF分析，回归分析结果如表3所示：

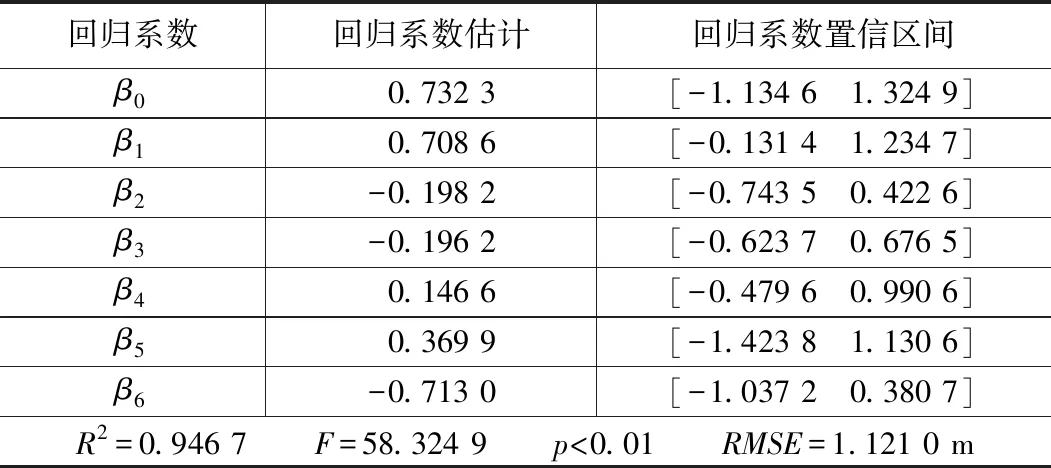
空间滤波模型估计结果 表3

以上结果均是在0.01显著性水平下得到的估计结果。显然，由表2和表3对比可以看出，在传统多元回归模型的基础上加入空间代理变量后的空间滤波模型，衡量模型拟合优度的判决系数R2从 0.701 9提高至 0.946 7，F统计量从 37.689 5增大到 58.324 9。RMSE从 1.437 4 m降低到 1.121 0 m。其次，空间滤波模型回归系数估计值以及回归系数置信区间相对于多元线性回归系数估计值以及置信区间也有所改善。

5 结论与展望

应用特征向量空间滤波，我们将多定位源空间布局这一重要因素通过空间代理变量加入多元线性回归模型中，进行多定位源数据融合分析。仿真分析表明，在多元线性回归模型的基础上加入空间代理变量可分离表征回归原始解释变量的空间自相关，消除回归变量系数估计的方差膨胀。特征向量空间滤波模型更加显著(统计模型更加符合实际定位源数据结构)，融合定位精度得到了进一步提高。

事实上，考虑空间结构信息(空间自相关效应)，不仅可以改善统计推断(参数估计和假设检验)准确性，而且可以优化统计抽样设计(即室内定位的定位源网络布设方案设计)。室内定位融合分析(统计推断)与室内定位源布设(统计抽样)存在辩证关系，优化室内定位源布局有助于提高室内定位精度。下一步，我们将继续考虑特征向量空间滤波模型来优化室内定位源观测网络布局。