两类矩阵对角化问题的研究

徐香勤

两类矩阵对角化问题的研究

徐香勤

河南牧业经济学院, 河南 郑州 450011

矩阵对角化在高等代数中占据着重要位置，成为求解矩阵论问题的必需工具。本文针对矩阵对角化的理论问题，利用Smith标准型，刻划了一类数字特殊分块矩阵可对角化的若干性质，并将结论推广到一般的域上。同时讨论了方阵族可同时对角化的充要条件以及正规矩阵族可同时酉对角化的充要条件。实例结果表明：两个对称正定（半正定）Hermit矩阵充要条件必要性是显然的，幂零阵的所有特征值都为零，＋和有相同特征值。

极小多项式; Simth标准型; 同时对角化; 特征值

高等代数是数学专业的必修课，而矩阵对角化则是高等代数的重要内容之一，在求解矩阵论问题时不可或缺。同时，矩阵对角化还在求解数列通项、微分方程以及信号处理、算法设计等领域都有很高的实用价值[1,2]。研究证明，实对称的矩阵一定能对角化，普通的数字矩阵不一定能对角化，但是两个普通的数字矩阵有可能同时对角化[3-6]。本文通过Smith标准型刻划一类分块矩阵可对角化的若干性质，并讨论可同时对角化方阵族的充要条件，给出了正规矩阵族可同时酉对角化的充要条件。本文中，表示复数集合，表示一个域，M()表示复数集上的阶方阵的集合。()表示方阵的全部特征值的集合。0∈()，0()={∈C|=0}称为关于特征值0的特征子空间。

1 方阵对角化的几个特质

引理1：∈M()，()为极小多项式，则可对角化的充要条件是()没有重根[7]。

引理2：数字方阵相似于数字方阵的充要条件是-等价于-[7]。

引理3：方阵可对角化的充要条件是的初等因子都是线性（无重根）[8]。

证明：的极小多项式和的极小多项式分别记为m()和m()，则m()=0。根据极小多项式的定义可知m()=0，于是m()|m()。由于可对角化，故m()没有重根，从而m()没有重根，因此矩阵可对角化。同理矩阵也可对角化。

证明：设-的Smith标准型为(1(),…,α())，设-的Smith标准型为(1(),…,β())。由于()∩()=，故：(β(),β())=1=1,2,…,;=1,2,…,(1)

考虑-的初等变换，可知其Smith标准型等价于：(1(),…,α(),1(),…,β()) (2)

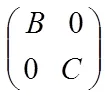
对于域上的矩阵，定理2有如下类似结论。

证明：充分性是显然的，以下证明必要性。

若可对角化，则的初等因子都是线性的，而的初等因子由和的初等因子合并组成，因此和的初等因子都是线性的，从而和都可以对角化。

2 同时对角化方阵族的几个性质

定理5：QÍM()为一个非空矩阵族，则Q可同时对角化的充要条件是：

（1）Q是可交换矩阵族；

（2）Q中每个矩阵均可对角化。

证明：任取1,2∈Q，存在可逆矩阵∈M()，满足-1AP=L,=1,2。从而12=L1-1L2-1=L1L2-1=L2L1-1=L2-1L1-1=21。必要性得证。

充分性：对矩阵的阶数采用数学归纳法。

=1结论是显然的。假设对所有阶数小于的矩阵结论均成立，以下考虑阶数为的矩阵。

若Q中每个矩阵均为数乘矩阵λI，结论显然成立。

若存在∈Q特征值个数至少为2，设存在可逆矩阵∈M()，使得：

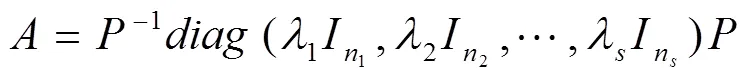
其中1，2，…，为的个不同的特征值(≥2)。

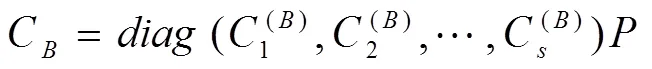
令：S={,λI|∈Q} (=1,2,…,) (5)

=(1,…,Q) (6)

从而对于"∈Q,()()-1为对角形。

考虑到正规矩阵（满足AA=AA）均可酉对角化[9]，利用与定理5相同的证明方法得以下结论：

推论1：QÍM()为一个非空正规矩阵族（Hermite矩阵族），则Q可同时酉对角化的充要条件是Q是可换族。

定理6：QÍM()为一个非空矩阵族，若Q是可换族，则Q可同时上（下）三角化。

证明:对矩阵的阶数采用数学归纳法。

=1是显然的。假设对所有阶数小于的矩阵结论均成立，以下考虑阶数为的矩阵。

情形1：若对于"∈Q,存在的一个特征子空间V0()的维数为,则必为数乘矩阵，此时定理成立；

情形2：$∈Q,存在的一个特征子空间V0()的维数小于,取出V0()的一个基1,2,…,α(<),将其扩充为C的一组基1,2,…,α,1,2,…,β(+=),令={1,2,…,α,1,2,…,β} (+=)，则：

注意到Q是可交换族，因此对于"∈Q,V0()均为的不变子空间，于是：

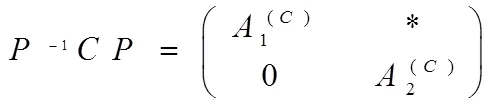
易知"∈Q，-1与-1均可交换，故1={|∈Q}È{0I}和诸2={(C)2|∈Q}È{2}是一个可交换族。由归纳假设矩阵族1,2可同时对角化。即存在可逆矩阵Q∈M()=1,2，使得"∈S，=-1 iLQ=1,2，其中诸L(∈Q)为对角形矩阵(=1,2)。令=(1,2)，易知对于"∈Q,()()-1为上三角阵。

考虑转置矩阵，可知Q可同时上（下）三角化。

推论2,∈M()。若=,1,2,…,λ是的全部特征值，1,2,…,µ是的全部特征值，则存在1,2,…,的排列,，使得λµ(i)(=1,2,…,)构成的全部特征值，λ+(i)(=1,2,…,)构成+的全部特征值。

3 两个例子

例1：,∈M()是两个对称正定（半正定）Hermit矩阵，则对称正定（半正定）的充要条件是＝。

证明：必要性是显然的，以下证明充分性。

若＝，由于Hermit矩阵是正规阵，根据推论1，则，可同时酉对角化。由推论2，的任意一个特征值必然为，其中∈()，∈()。当都正定时，>0（当都半正定时，≥0），故正定（半正定）。

例2：∈M()是一个幂零阵，＝，则det (＋)＝det ()。

证明：由于是一个幂零阵，因此的所有特征值都为零，由引理2，＋和有相同的特征值，故det (＋)＝det ()。

4 讨论

矩阵的理论和方法已成为现代科技领域必不可少的工具，当今电子计算机及计算技术的迅速发展为矩阵理论的应用开辟了更广阔的前景。矩阵对角化作为矩阵论的重要组成部分,对其研究主要集中在各类特殊矩阵可对角化对的条件判定以及相关应用。邓勇对主理想环上矩阵可对角化问题进行了探讨，给出了主理想环上一类具有特殊类型最小多项式的矩阵可对角化的充要条件[9]。程薇给出了一个四元数矩阵对同时实对角化的定义，讨论了两个四元数矩阵可同时实对角化的充分必要条件并给出了可行的算法，讨论了一个四元数长矩阵集可同时实对角化的情况[10]。Choreño E和Zhou J等人利用对角化方法在较好地解决了-光子-模型的求解问题[11,12]。相对而说，矩阵对角化的理论研究滞后于实践应用，但随着学者们的广泛重视，在理论研究方面将会有较大的进展。

5 结论

求解矩阵对角化的理论问题有较大的研究价值，本文通过Smith标准型刻划了一类数字特殊分块矩阵可对角化的若干性质，并将结论推广到一般的域上。同时讨论了方阵族可同时对角化的充要条件，以及正规矩阵族可同时酉对角化的充要条件。最后利用文中定理，通过实例证明了两个矩阵论中的结论。

[1] 岳嵘.利用矩阵对角化求数列通项[J].高等数学研究,2007,10(4):66-68

[2] 龚丽燕,陈益智,蔡俊树.递推数列通项的矩阵解法[J].高等数学研究,2014(5):3-6

[3] 李丽花.矩阵可对角化问题的研究[J].考试周刊,2012(64):48-48

[4] 赵利强,陈坤云,王建林,等.基于矩阵对角化变换的高阶容积卡尔曼滤波[J].控制与决策,2016,31(6):1080-1086

[5] 汪芳宗,王永,宋墩文,等.基于矩阵对角化的电磁暂态时间并行计算方法[J].电网技术,2017,41(8):2521-2527

[6] 韩如意,王川龙.对称矩阵填充的线性交替最速下降算法研究[J].中北大学学报:自然科学版,2018,39(1):14-20

[7] 陈公宁.矩阵理论与应用[M].北京:高等教育出版社,1990:72

[8] Horn RA, Johnson CR. Matrix Analysis[M]. Cambridge: Cambridge University Press 2012:137

[9] 邓勇.主理想环上矩阵可对角化的新判据[J].山东农业大学学报:自然科学版,2015,46(4):625-627

[10] 程薇.四元数矩阵代数中的若干问题研究[D].北京:国防科学技术大学,2009

[11] Choreño E, Ojeda-Guillén D, Granados VD. Matrix diagonalization and exact solution of the k-photon Jaynes–Cummings model[J]. The European Physical Journal D, 2018,72(8):142-157

[12] Zhou J, Su HY, Zhang FL,. Solving the Jaynes-Cummings Model with Shift Operators Constructed by Means of the Matrix-Diagonalizing Technique[J]. Chinese Physics Letters,2018,35(1):15-18

Study on Diagonalization of Two Kinds of Matrices

XU Xiang-qin

450011,

Matrix diagonalization plays an important role in Higher Algebra and becomes a necessary tool for solving matrix theory problems. In this paper, some properties of the diagonalization of a class of special block matrices are characterized by using Smith's canonical form, and the conclusion is extended to the general field F. At the same time, the necessary and sufficient conditions for the simultaneous diagonalization of square matrices and the simultaneous unitary diagonalization of normal matrices are discussed. The results show that the necessary and sufficient conditions for two symmetric positive definite (semi-positive definite) Hermit matrices are obvious. All eigenvalues of nilpotent matrix A are zero, and A+B and B have the same eigenvalues.

Minimal polynomial; smith form; simultaneous diagonalization; eigenvalue

O151.21

A

1000-2324(2019)02-0350-03

10.3969/j.issn.1000-2324.2019.02.037

2018-03-04

2018-05-12

河南省科技厅软科学研究计划项目(182400410584)

徐香勤(1979-),女,硕士,讲师,主要研究方向为矩阵论、偏微分方程、应用数学. E-mail:xiangqinxu@163.com