基于竞争失效的综合传动剩余寿命预测*
闫书法,马 彪,郑长松
(北京理工大学机械与车辆学院,北京 100081)
前言
随着工业科技的快速发展和全球化竞争的日益激烈,现代军用装甲车辆传动系统呈现出规模大、复杂度高和效率高的发展趋势,机械传动系统的可靠性与安全性受到了广泛的重视[1]。车辆综合传动装置作为复杂时变的机电系统,在高速重载的运行过程中,齿轮、摩擦片和轴承等关键零部件会不断地磨损,当磨损经过一段时间的积累期并达到一定的阈值后,会导致综合传动装置损伤的出现,如果不能及时地发现和预防,最终会导致综合传动装置的失效[2]。一旦发生失效事故,所造成的军事和经济损失往往是不可估量的。因此,必须采取积极主动的方法,在综合传动失效之前,准确地制定视情维修策略。因此,通过综合传动装置的运行状态监测数据,对综合传动装置开展状态监测与寿命预测研究,进而实现综合传动装置的预防性维修是保障其可靠运行的切实可行的方法。
目前针对综合传动装置的状态监测与寿命预测问题,已有学者利用油液光谱数据开展了部分研究工作[3-7]。这些代表性研究只考虑了一元劣化失效模式下的劣化建模与寿命预测问题,针对复杂失效模式的研究较少,主要有两方面原因:(1)综合传动装置的状态监测数据具有高维非线性的特点,状态监测信息的合理利用较为困难;(2)综合传动装置是一个复杂时变的机电系统,具有多种失效过程,失效机理复杂,失效模型的准确建立较为困难。
针对综合传动装置等复杂装备存在多劣化失效模式问题,本文中提出了一种基于劣化失效和突发失效竞争的剩余寿命预测方法。针对综合传动装置的多维状态监测数据,采用主元分析和状态空间模型融合劣化监测数据;采用随机过程Wiener模型建立装置劣化失效模型,采用Weibull分布模型建立装置突发失效模型,进一步在劣化失效与突发失效相关的基础上建立综合传动装置竞争失效模型;最终实现综合传动装置的剩余寿命预测。
1 综合传动装置竞争失效模型
为及时掌握综合传动装置的磨损状态并准确实施预防性维护策略,避免异常停机的产生,提高综合传动装置的可维护性与可靠性,有必要在竞争失效框架下开展综合传动装置的剩余寿命预测工作。基于劣化失效和突发失效竞争的综合传动装置剩余寿命预测框架如图1所示。
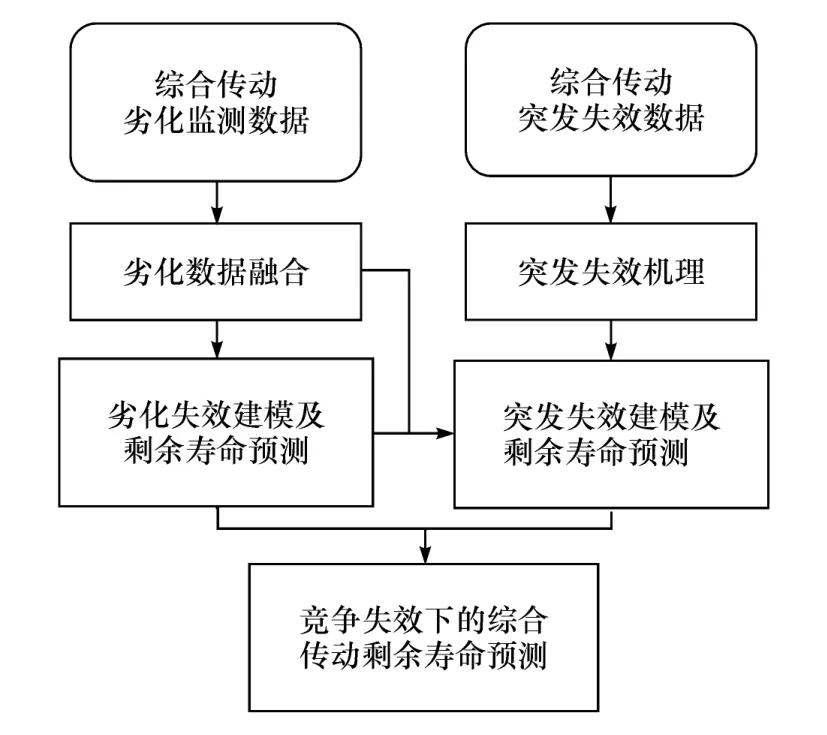
图1 竞争失效下的综合传动剩余寿命预测框架
1.1 多维劣化数据的数据融合
综合传动装置的主要磨损部位包括湿式离合器、齿轮、密封环、轴承和汇流行星排等,磨损零部件众多,磨损机理复杂[2]。金属磨粒作为主要的磨损产物,来自于不同的摩擦副表面且在油液中均匀混合。MOA II原子发射光谱仪可分析油液中微小磨粒的元素浓度,实现基于磨粒元素浓度的磨损劣化建模。然而,由于油液光谱数据众多,信息冗余量大,无法直接将光谱测量数据用于综合传动装置的磨损劣化建模。
核主元分析方法可有效降低光谱数据的变量维数,利用较少维数的主元代替原来较多的变量,并能够反映原来的变量信息,在求解特征变量中得到了广泛的应用。但是,核主元分析方法对数据样本点分布特征具有较大的敏感性,且当测量数据中存在离群值时,会对分析结果产生较大的影响[8]。针对传统核主元分析对测量数据样本点分布特征和离群值敏感性的问题,基于模糊隶属度的核主元分析是一种行之有效的方法。但该方法仅是将数据集划分为一个类,并未有约束条件。为此,Ichihashi[9]提出了一种熵劣化函数:

式中:等号右侧第1项为重构误差的加权和;等号右侧第2项为正则化项;e(xi)为真实值与估计值的均方误差;ui为隶属度。对式(1)求导可得 ui=exp(-e(xi)/σ2),可以看出,e(xi)越小,表示估计值与真实值越接近,隶属度 ui越大;反之,e(xi)越大,真实值为离群值的概率越大。
将模糊隶属度赋予特征空间中的数据集,在核主元分析的特征空间中对测量数据进行鲁棒改进,最终形成鲁棒核主元分析方法,以减少离群值对核主元分析过程的影响。具体分析方法如下:
(1)初始化隶属度 U0=(u1,u2,…,u3)=(1,1,…,1),在 t=0时计算主元矩阵 V0;
(2)令 t=t+1,计算矩阵 K,~K,得到特征值 λk和特征向量αk,进而计算隶属度向量Ut;
(3)如果 max|uti-1-uti|<ε,则进行下一步,否则返回第2步;
(4)计算观测数据 xi(j=1,2,…,n)投影于特征向量 vk(k=1,2,…,p)上的投影值,则基于模糊隶属度的鲁棒主元为

综合传动装置的性能状态可分为健康状态、报警状态和失效状态[7]。其在健康状态和报警状态的油液光谱数据矩阵的特征矩阵具有不同的数据结构和不同的状态子空间。假设综合传动装置在健康状态的状态子空间为S0,在劣化时刻t的状态子空间为St,通过空间基向量的主夹角表示两类状态子空间的相似性。Hamm等[10]提出了一种基于基矢量内积矩阵奇异值分解的主夹角数值计算方法。基向量的内积矩阵为

对内积矩阵进行奇异值分解,得到特征值k1,k2,…,kd,计算特征值的反余弦值,即可得到主夹角:

式中 0≪θi≪π/2,θi越小,说明 S0与 St之间的相似性越大,综合传动装置的劣化程度越低。
得到主夹角向量为 θ=(θ1,θ2,…,θi),最小主夹角min(θi)体现了状态子空间 S0与St的最主要的相似信息。因此,利用min(θi)的正弦值表示综合传动装置的劣化程度:

式中劣化程度τ的取值范围为[0,1]。健康状态时劣化程度τ趋近于0,失效状态时劣化程度τ趋近于1。
1.2 劣化失效模型
综合传动装置中的金属磨粒主要由磨损过程产生,由于磨损程度变化的不确定性,金属磨粒的生成可以被近似为扩散过程,即是由布朗运动驱动的连续时间连续状态的随机过程。近年来,在描述系统随机劣化过程中,Wiener过程模型得到了广泛应用[11]。因此,本文中采用状态监测数据,利用Wiener过程模型对综合传动装置劣化过程{τ(t),t≥0}进行建模。
一般来说,基于Wiener过程的系统劣化模型可具体描述为

式中:劣化过程{τ(t),t≥0}是由标准布朗运动{B(t),t≥0}驱动的;σ为扩散系数;θ为漂移系数;且有 σB(t)~N(0,σ2t),以用来表示劣化过程的随机性和随时间变化的不确定性。不失一般性,本文中令初始劣化状态等于0,即 t=0时,τ(0)=0,则劣化过程在 t时刻为正态分布,即 τt~N(θt,σ2t)。劣化状态的概率密度函数(probability density function,PDF)为

通过随机劣化过程首中时间(first hitting time,FHT)的概念来定义综合传动装置的寿命,即如果随机劣化过程{τ(t),t≥0}首次达到预先给定的失效阈值,则认为综合传动装置失效,需要进行维护。根据首中时间的概念,给定失效阈值为ω,综合传动装置的寿命T定义为
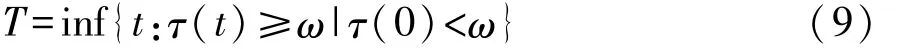
根据随机过程理论可知,Weiner过程到达固定阈值的首中时间为逆高斯分布,因此,在当前劣化状态 τk(τk<ω)已知的情况,寿命 T具有如下性质[12]:
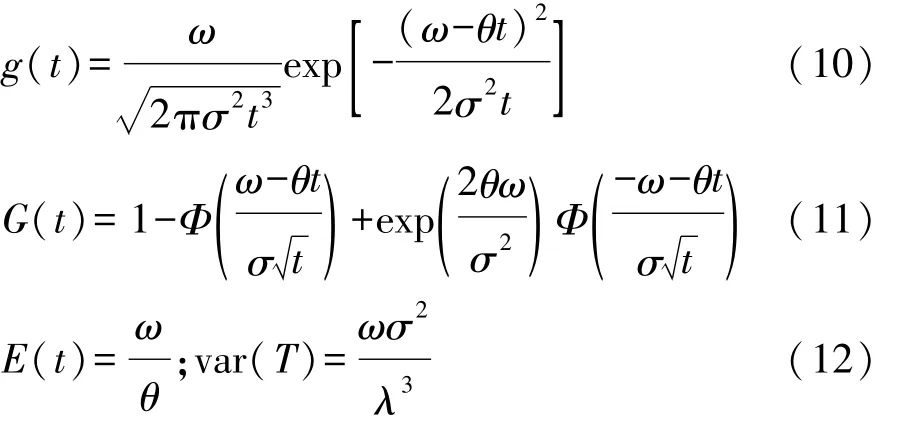
1.3 突发失效模型
在工程实际中,设备的突发失效一般采用Weibull分布描述,且突发失效概率受设备劣化程度的影响,即劣化程度越大,突发失效的可能性越高。假设综合传动装置的突发失效时间ξc符合Weibull分布,形状参数b与劣化程度τ无关,尺度参数η与劣化程度τ有关,关系为η=a/τ。则突发失效的故障率函数为

综合传动装置突发失效时间的概率密度函数(PDF)和累积分布函数(cumulative density function,CDF)为

1.4 竞争失效模型
根据前述内容,综合传动装置在竞争失效模式下的可靠度函数为
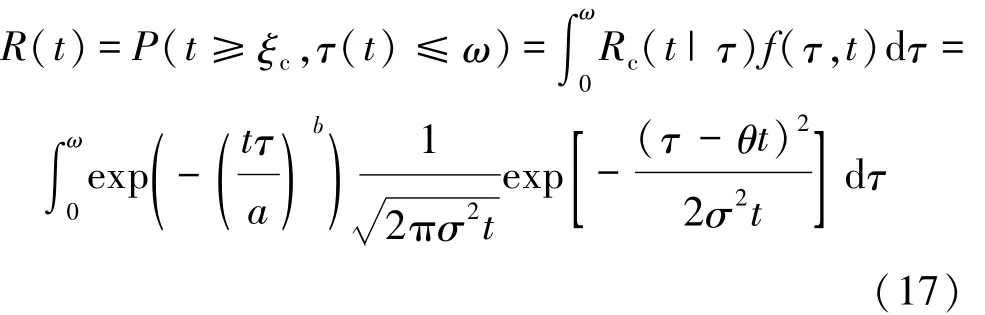
如果劣化失效与竞争失效不相关,则综合传动装置的可靠度函数为
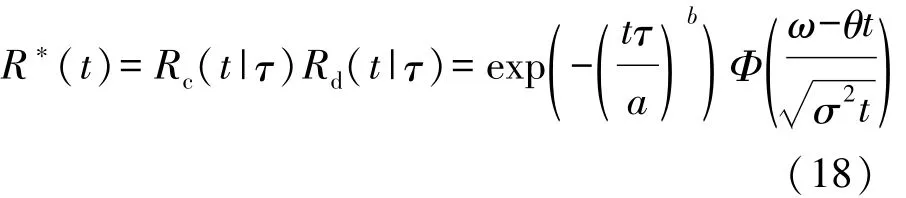
2 参数估计与剩余寿命的估计
为实现综合传动装置的剩余寿命预测,需要利用历史失效数据确定失效模型的参数。假设一共有M+N台综合传动装置,其中因为劣化失效而发生故障的有M台,因为突发失效而发生故障的有N台。
根据综合传动装置全寿命实验油液光谱测量数据,利用1.1节的数据融合方法得到综合传动装置在时间ti的劣化程度τi,然后利用极大似然方法估计劣化失效模型参数。根据式(8),第k台综合传动装置在第i观测时刻的性能劣化程度的概论密度函数(PDF)为[13]
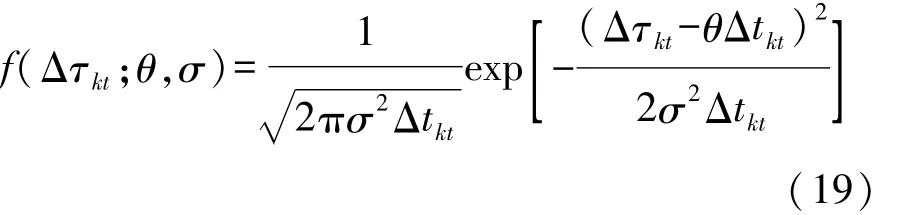
则似然函数为

对上式两边取对数,然后对θ和σ2求偏导,并令偏导数为0,即可求得θ和σ2为

根据N台发生突发失效的综合传动装置的突发失效时间(ξc1,ξc2,…,ξcN),以及相对应的性能劣化程度(τ1,τ2,.,τN),根据式(14)得到突发失效的似然函数为
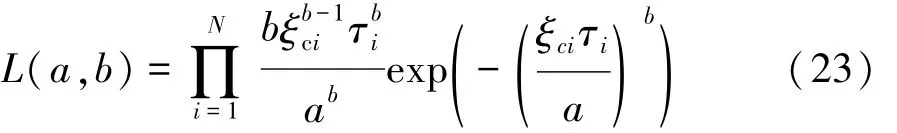

综合传动装置运行至t时刻时的剩余寿命为

3 实验研究
综合传动装置是基于双功率流传动原理,集变速、转向和制动等机构于一体的复杂机电系统,主要零部件包括:前传动装置、传动齿轮、多片湿式离合器、液压换挡阀和柱塞泵电机等,其系统构成如图2所示。
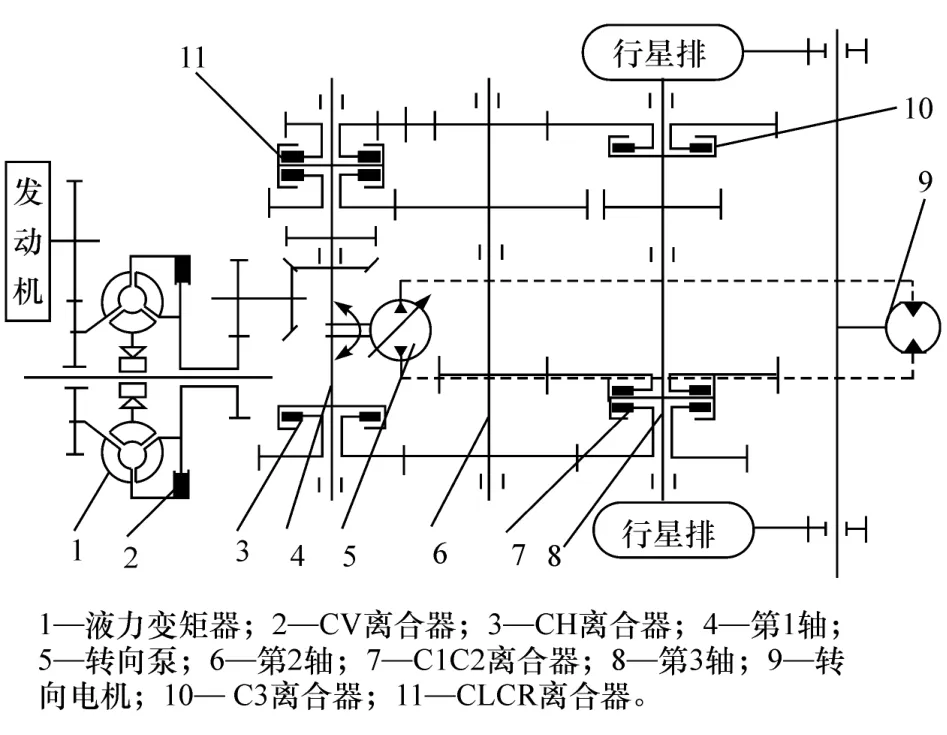
图2 综合传动系统构成示意图
以综合传动装置状态监测数据中的油液光谱金属元素浓度为劣化监测数据,以突发失效时间作为突发失效数据,应用本文中提出的竞争失效分析方法,就可实现综合传动装置的剩余寿命预测。本文中研究所用的失效数据来自于综合传动装置全寿命周期可靠性实验,实验台如图3所示。
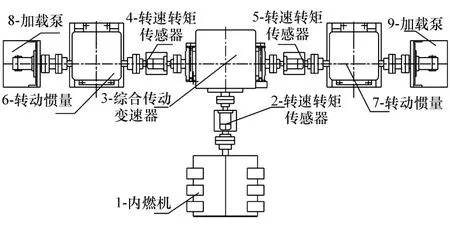
图3 综合传动全寿命磨损实验台
依据可靠性实验大纲,实验工况为多挡位、变负荷、多转速循环工况,油液取样位置为精滤器上游,取样时间区间为30-250 h,取样间隔为10 h,具体的取样操作规范与原则可以参见文献[6]。其中一台综合传动装置在运行至253 h时发生故障,在失效之前共取得24个实验油液样本。
采用MOA II型原子发射光谱仪,对上述24个综合传动装置磨损实验油液样本进行分析,得到21种常见元素的光谱分析浓度值数据,根据文献[6]剔除油液光谱数据中与表征综合传动装置磨损状态无关的元素,最终得到表征综合传动装置劣化状态的元素光谱数据,如表1所示。

表1 综合传动装置可靠性实验光谱数据
针对表1中的油液光谱数据,利用1.1节的数据融合方法,得到综合传动装置在各测量时刻的劣化程度,如表2所示。
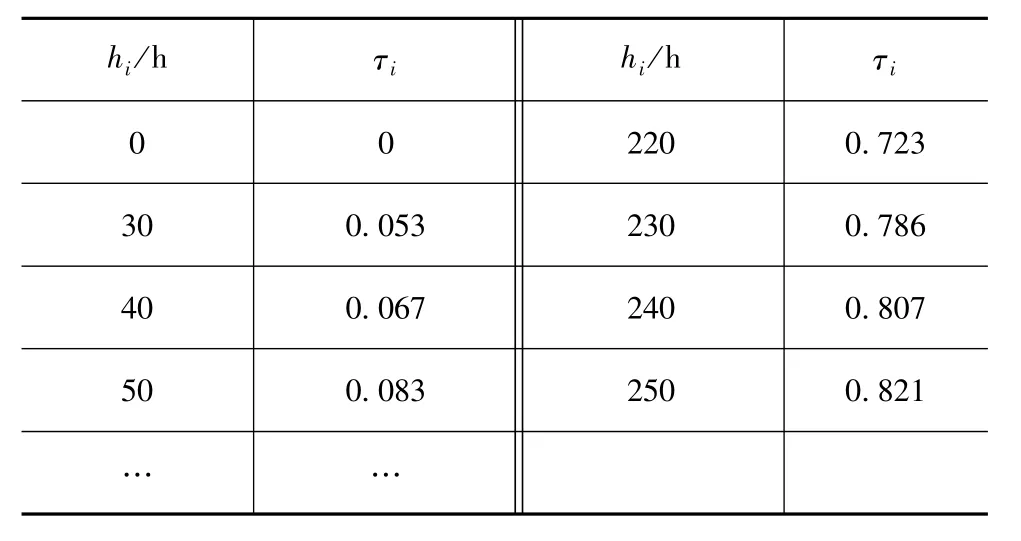
表2 综合传动装置性能劣化程度
为实现综合传动装置的劣化失效建模,需要利用性能劣化监测历史数据确定劣化失效模型的参数σ2,θ。根据式(21)和式(22),利用极大似然方法估计得到劣化模型参数为=0.00331,=0.00027。
已知同型号5台发生突发失效的综合传动装置的失效时间数据和相应的劣化状态如表3所示。

得到的综合传动装置在竞争失效模式下的可靠度曲线如图4所示。其中R(t)为本文中提出的竞争失效模式下的可靠度曲线,R*(t)为劣化失效与突发失效不相关的竞争失效模式下的可靠度曲线,Rd为仅考虑劣化失效模式下的可靠度曲线。
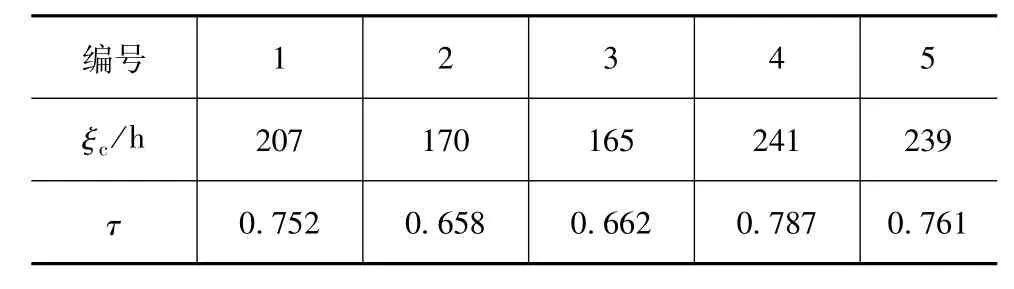
表3 综合传动装置突发失效数据

图4 综合传动装置可靠度曲线
由图4可知,在综合传动装置的任意工作时刻,Rd(t)恒大于等于 R*(t),即仅考虑劣化失效对综合传动装置进行可靠度估计会导致可靠度估计结果偏大;R(t)恒小于等于 R*(t),说明考虑竞争失效的可靠度估计结果较为稳健,这有利于对综合传动装置的安全评估和预防性维护。
进一步,利用蒙特卡罗方法对式(24)进行随机抽样平均,得到竞争失效模式下的综合传动装置的寿命估计值ξ为253.7 h。为验证基于劣化失效和突发失效竞争的综合传动装置寿命估计方法的准确性,定义剩余寿命估计值与对应真实剩余寿命的相对误差为

应用式(26),分别在综合传动装置运行至第50,110和170 h时,计算并比较考虑竞争失效和仅考虑劣化失效时剩余寿命估计与对应真实剩余寿命的相对误差,如表4所示。
由表4可见,本文中提出的考虑劣化失效与突发失效竞争的综合传动装置剩余寿命预测方法具有较小的相对误差,能够提高剩余寿命预测的准确性,这为综合传动装置的视情维修策略的合理制定提供了有益的参考。
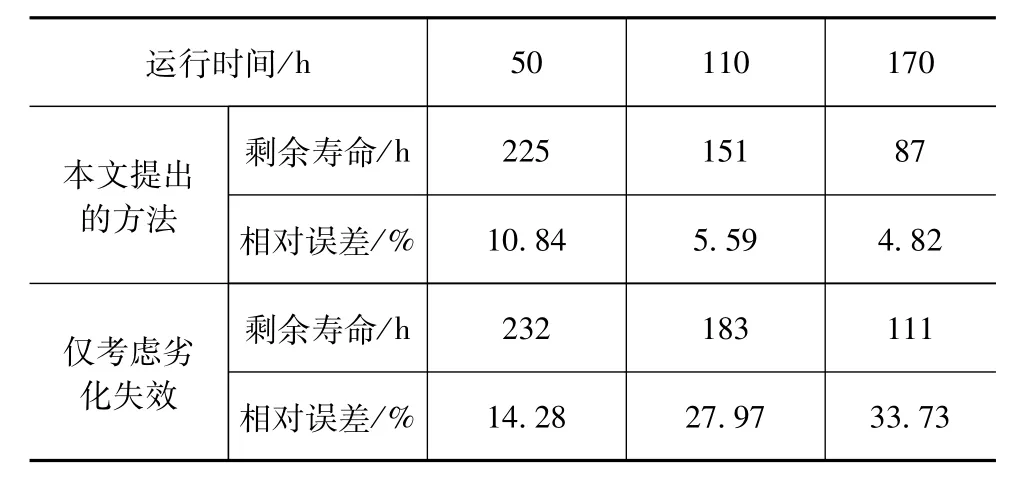
表4 估计的平均剩余寿命和相对误差
4 结论
为提高综合传动装置可靠性建模的合理性和剩余寿命预测的准确性,本文中研究了基于劣化失效模式和突发失效模式竞争失效的综合传动装置剩余寿命预测方法,具体结论如下。
(1)基于主元分析与状态空间模型的多维劣化数据融合方法能够有效降低综合传动装置状态监测数据的变量维数,将性能劣化数据有效的融合,并能够反映原来的状态信息,为综合传动装置的劣化失效建模及剩余寿命预测提供了基础,对其它具有多维监测数据的装备劣化指标融合具有借鉴意义。
(2)考虑综合传动装置劣化失效与突发失效竞争的可靠性建模与剩余寿命预测方法,能够建立装备性能劣化与突发失效之间的作用机制,能够客观地描述综合传动装置的性能劣化与失效机理,为深入了解综合传动装置的失效机理和规律提供了有益的参考。
(3)综合传动装置全寿命实验表明,与仅考虑劣化失效的剩余寿命预测结果相比,本文中提出的方法得到的剩余寿命预测结果具有较小的相对误差,与综合传动装置的真实剩余寿命更为接近,预测结果更为准确,有利于综合传动装置视情维修策略的合理制定。

