三维内埋式航弹与载机分离非定常流场数值模拟

李 菁，陈 帮,胡俊香

(1.安徽神剑科技股份有限公司， 合肥 230000； 2.陆军南京军代局， 南京 210024)

机弹分离过程中，载机和航弹间会产生复杂的非定常气动干扰，特别是在分离初期，气动干扰会使航弹的气动力特性和飞行特性产生很大的变化，影响到安全分离，甚至可能会造成弹体与载机相撞的飞行事故。因此研究载机与航弹分离的非定常流场[1-3]，分析航弹发射过程中机弹气动干扰力以及分离过程中弹的气动特性及气动干扰机理十分必要。基于动态网格[4-6]的CFD计算技术是近年计算流体动力学最新发展成熟的重大成果，用于解决由于流场边界运动造成的流场域随时间变化解算问题，动网格耦合求解Euler/N-S方程和弹道方程可用于模拟分离和多体相对运动的非定常复杂流场。

1 国内外研究概况

从20世纪90年代开始，求解Euler/N-S方程及弹道方程的数值模拟方法的研究大部分采用准定常方法，如Rainaidd、 Gillybeof等[7-9]进行的研究。结果表明，在预测弹体分离轨迹等方面与实验得到的结果较为一致，但无法准确得到多体分离过程中的非定常流场气动参数。21世纪，Pieter、KAC和KDA公司等[10-14]在数值模拟方法对分离问题进行的研究有了新成果。随着动网格技术的发展，国外采用各种动网格技术并耦合求解Euler/N-S方程和弹道方程来模拟分离和多体相对运动的非定常复杂流场。Baum和Loher等[15]研究了采用非结构动网格技术及耦合求解Navier-Stokes方程和弹道方程的非定常数值模拟方法，并成功应用于机载外挂物分离、飞行员及座椅与载机的分离等问题的研究。

国内采用准定常数值模拟方法研究多体干扰流场的工作取得了大量的成果，而采用非定常方法耦合求解N-S方程及弹道方程研究多体干扰分离问题的工作仍处于起步阶段。20世纪90年代开始，机弹分离[16]与气动干扰问题日益突出。上海大学、上海交通大学1011研究室等[17-19]对飞机外挂分离过程的机弹干扰问题进行了卓有成效的研究。随着航空航天飞行器的发展，CFD工作者逐渐展开了耦合求解N-S方程及弹道方程的非定常数值模拟方法研究。从成果看，数值方法能很好地捕捉机弹干扰复杂流场的流动特性，机弹干扰的流场复杂，对于不同的发射条件和导弹挂载方式的不同，导弹分离受到的干扰程度和规律有所不同。

2 计算模型及计算条件

以长深比L/D为三维空腔作为载机的内埋弹舱计算模型，对三维内埋式航弹与载机的非定常分离过程进行了数值模拟。其中初始时刻航弹与载机内埋弹舱的相对位置示意图如图1，航弹三维计算外形如图2。

采用非结构网格对内埋式航弹与载机分离的非定常流场区域进行离散，计算时首先保持弹体与载机内埋弹舱空腔的初始相对位置不变进行定常计算获得一个定常解，然后在此基础上再开始自由投放进行非定常动态网格数值计算。

计算条件为：L/D=3；来流Ma=2，；α=0°,2°,4°；航弹初始下抛速度为Vs0=10 m/s，15 m/s；气压为30 116.5 Pa，温度为228.2 K。

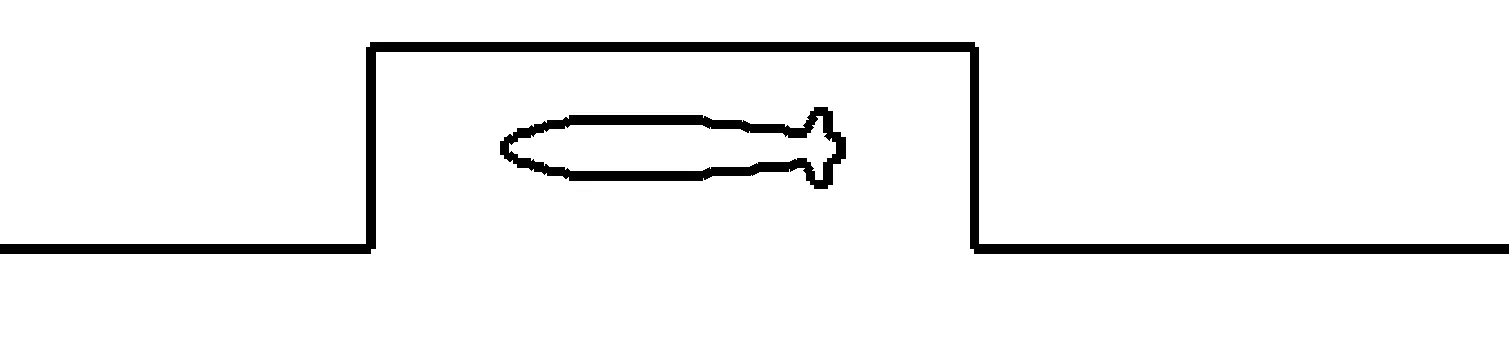
图1 三维机弹分离计算模型对称面示意图

图2 三维航弹计算模型示意图

3 非定常数值模拟结果

3.1 非定常流场数值模拟结果

图3～图6为L/D=3，Vs0=10 m/s，Ma=2，α=0°条件下分离过程中不同时刻航弹对称面的等压力线图。从图3～图6可以看出，在机弹分离的过程中，载机弹舱敞开后，在弹舱空腔和航弹间存在强烈的气动干扰，这种干扰随着航弹与弹舱间距的增大逐渐减弱。当来流为超音速时，弹舱空腔前缘出现激波，在分离过程中，航弹要穿过此激波，导致弹体气动力变化剧烈。当航弹穿过弹舱空腔前缘激波后，就不再受弹舱空腔周围流动的影响，即脱离了弹舱干扰区。

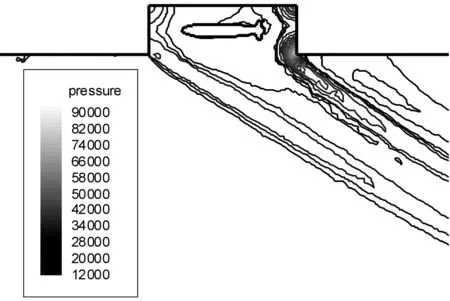
图3 T=0 s时航弹对称面的等压力线

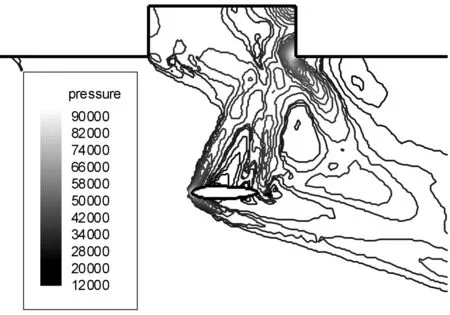
图5 T=0.4 s时航弹对称面的等压力线

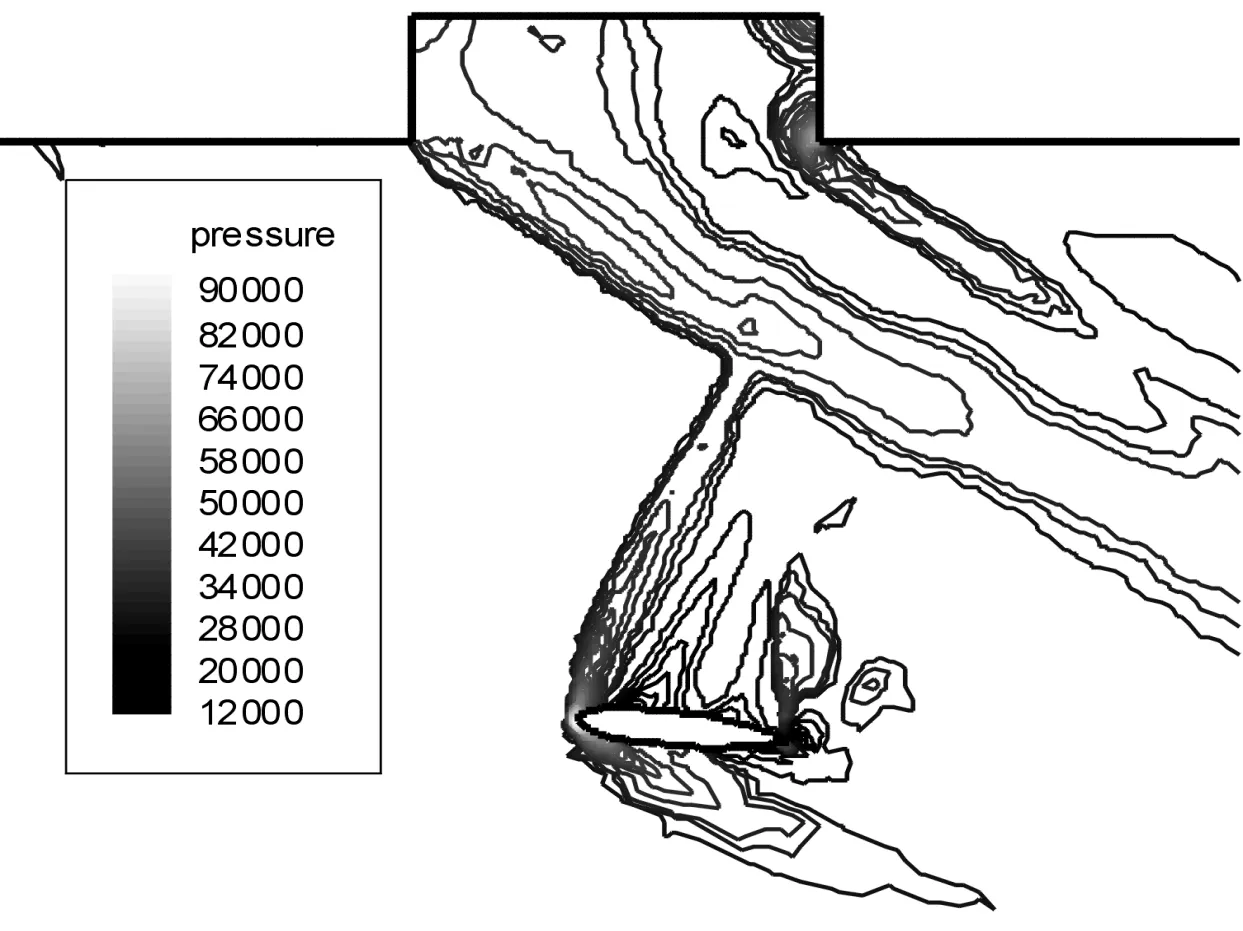
图6 T=0.6 s时航弹对称面的等压力线

3.2 非定常分离过程中航弹气动特性变化规律

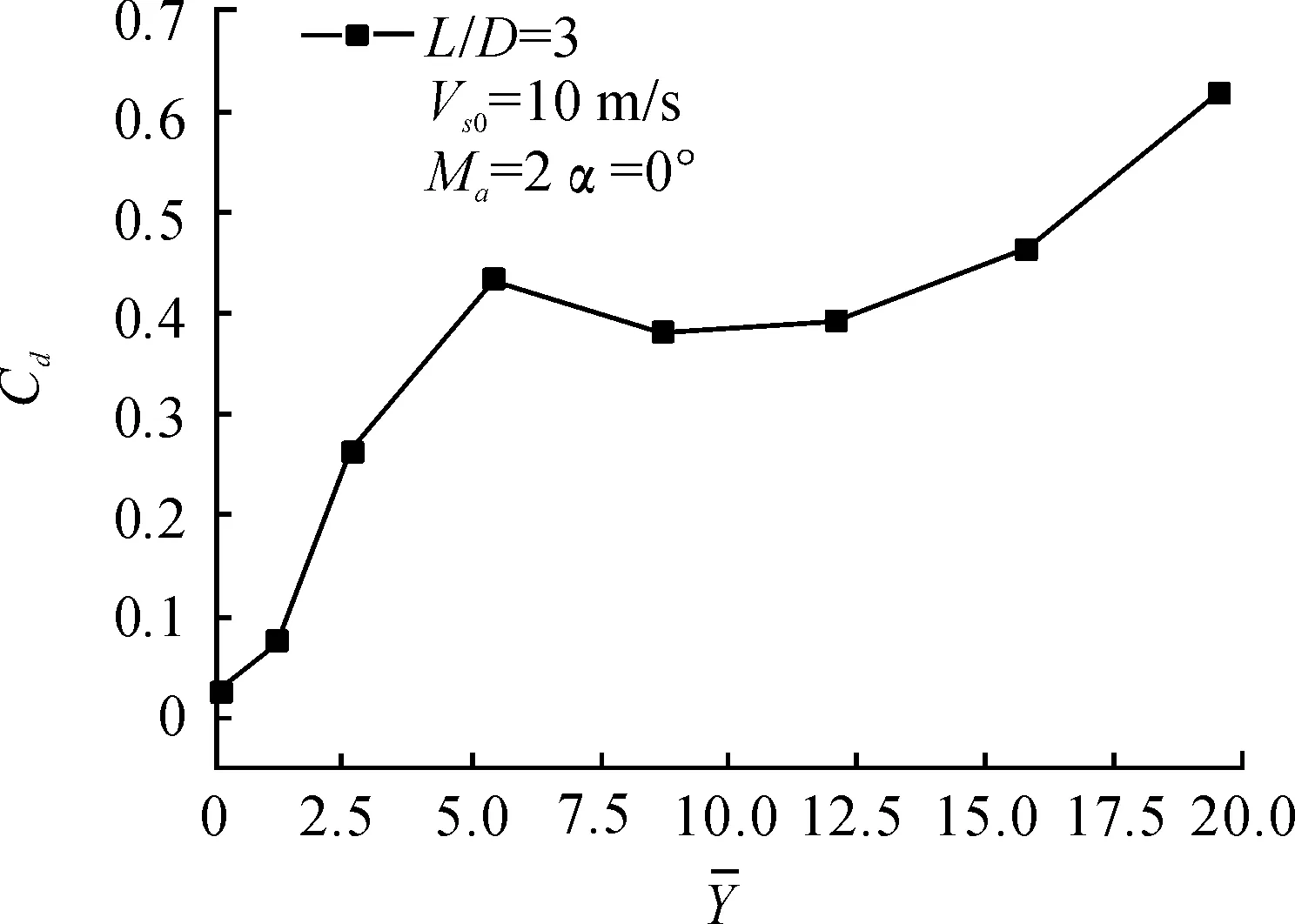
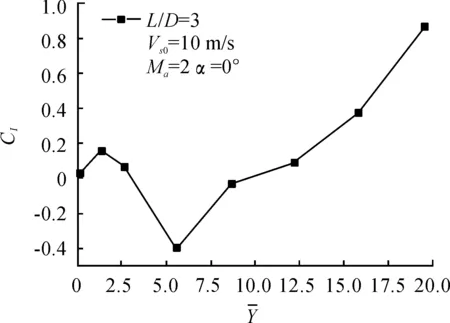
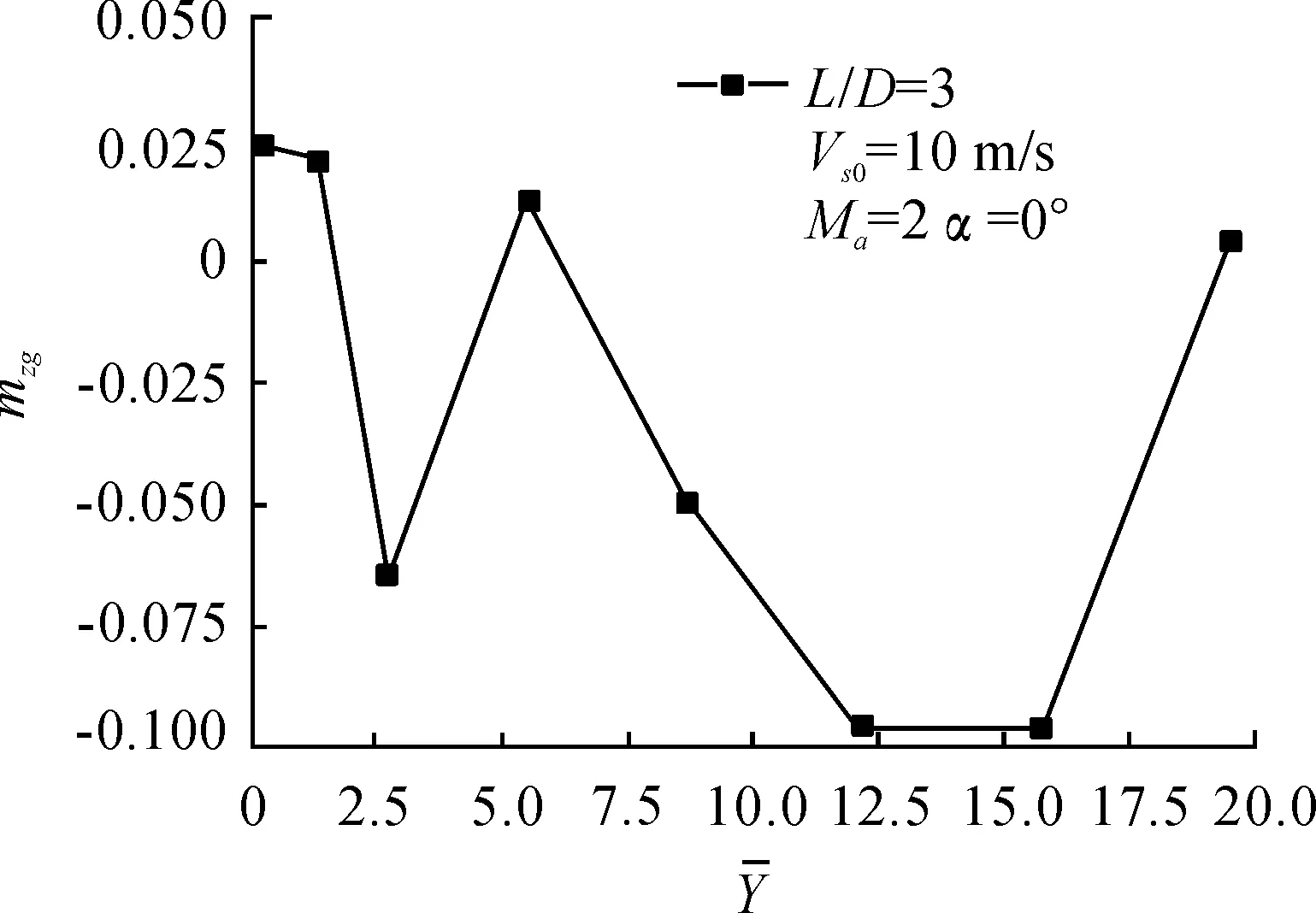
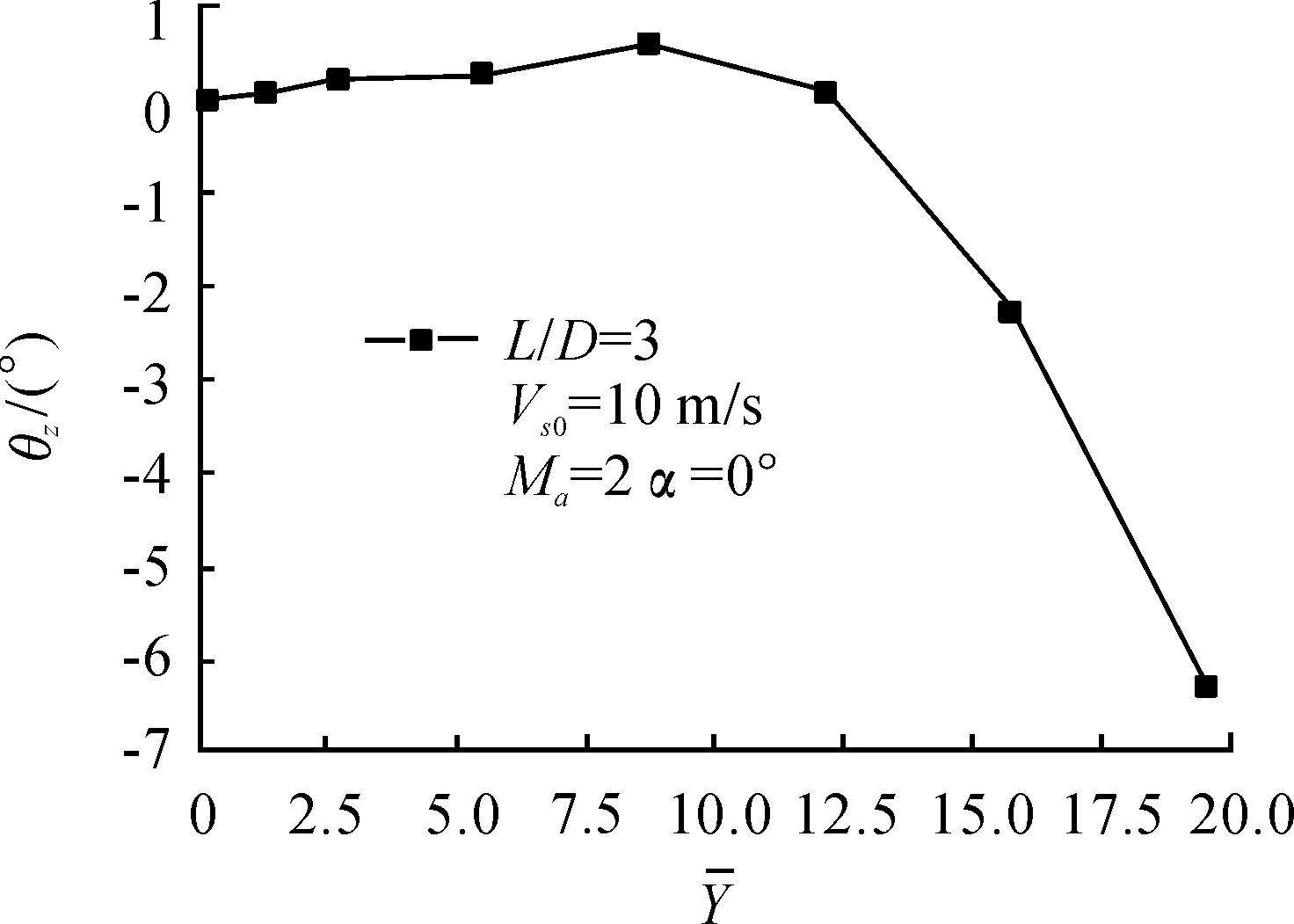
图7～图10所示为机弹分离过程中，当来流马赫数为Ma=2、来流攻角为α=0°,航弹初始下抛速度为Vs0=10 m/s时，航弹的阻力系数、升力系数、俯仰力矩系数和姿态角随机弹间距变化曲线。

图曲线

图曲线

由图7可看出，航弹的阻力系数随着机弹间距的增大呈增大趋势，且在空腔近区变化较大，但是到一定距离以后变化趋于平缓，当航弹脱离载机的干扰区后，又有一个大的变化。

由图8可看出，航弹在初始下抛的过程中，升力系数为正，随着机弹间距的增大，升力系数逐渐变为负值，随后又变为正值，且随机弹间距增大而增大。

图曲线

图曲线

由图9可看出，在分离过程中，航弹的俯仰力矩变化剧烈，呈振荡变化。

由图10可看出，随着机弹间距的增大航弹的姿态角先为小的正值，当机弹间距增大到一定程度后，姿态角变为负值，且随着机弹间距离增大，负值增大。

造成航弹气动力剧烈变化的原因主要是，机弹间距较小时载机武器舱敞开舱室对航弹周围流场的干扰剧烈引起的。

图11和图12分别是分离过程中，航弹姿态角随时间变化曲线和机弹垂向间距随时间变化曲线。可看出，随着下落时间的增加，航弹下落速度加快，且航弹的姿态角先为小的正值，后变为负值，且负值逐渐增大。

3.3 航弹初始下抛速度对非定常分离的影响

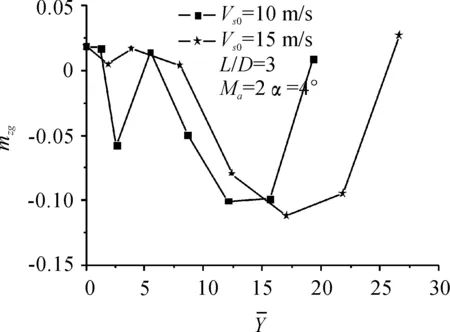
图13～图16所示为机弹分离过程中，在来流马赫数为Ma=2，来流攻角为α=4°，航弹初始下抛速度为Vs0=10 m/s和15 m/s时，航弹的阻力系数、升力系数、俯仰力矩系数和姿态角随机弹间距变化曲线。

由图13～图16可以看出，当航弹初始下抛速度为Vs0=10 m/s时，分离过程中其气动特性变化较大。当航弹下抛速度增大到Vs0=15 m/s时，情况有明显改善，易分离。

图17和图18分别是不同的航弹初始下抛速度的情况下，在机弹分离过程中，航弹姿态角随时间变化曲线和机弹垂向间距随时间变化曲线。

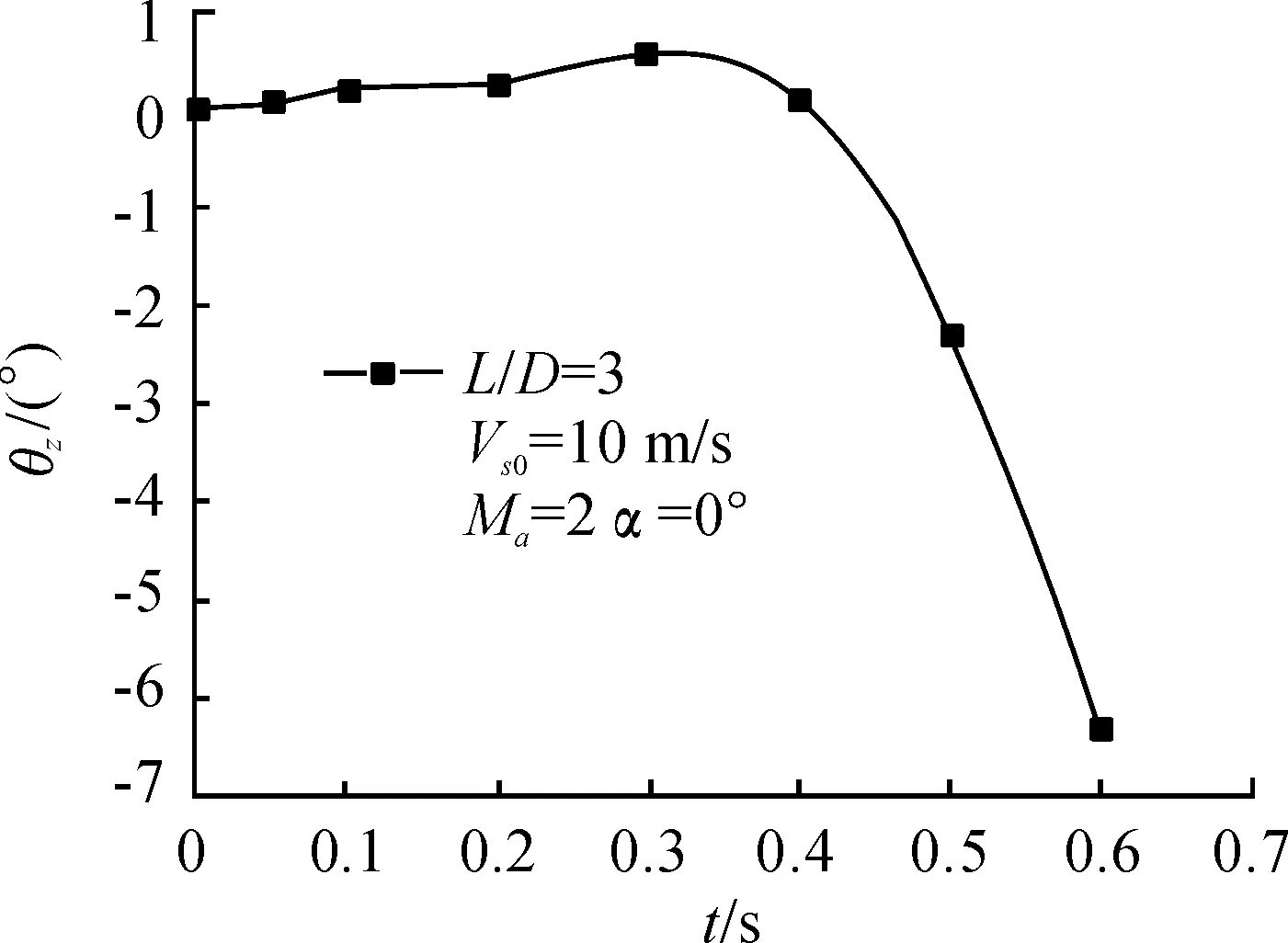
图11 姿态角随时间的变化曲线

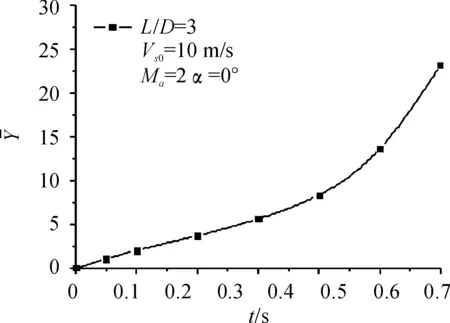
图12 机弹垂向间距随时间变化曲线

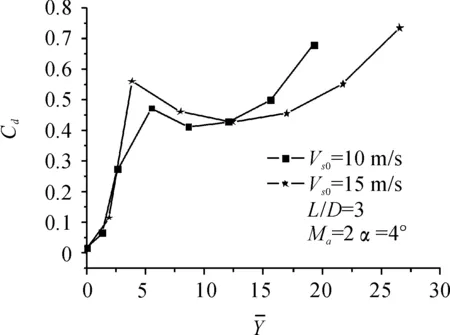
图曲线

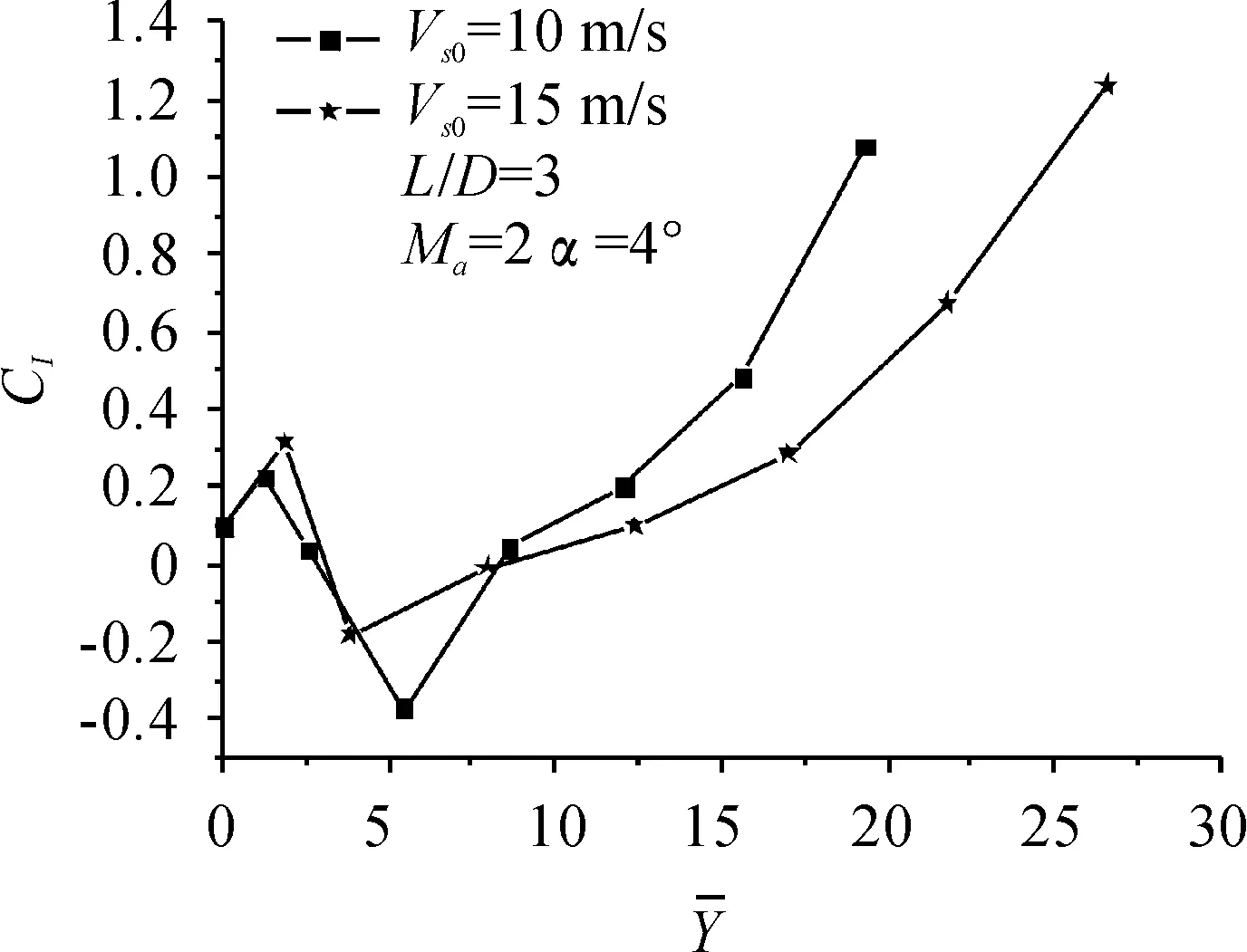
图曲线

图曲线

图曲线

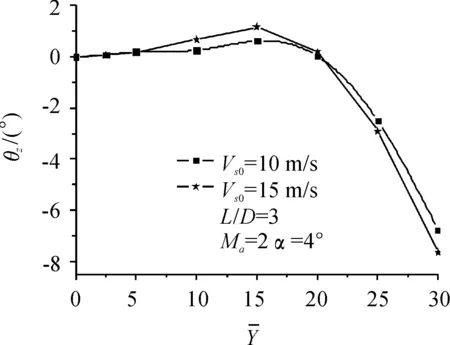
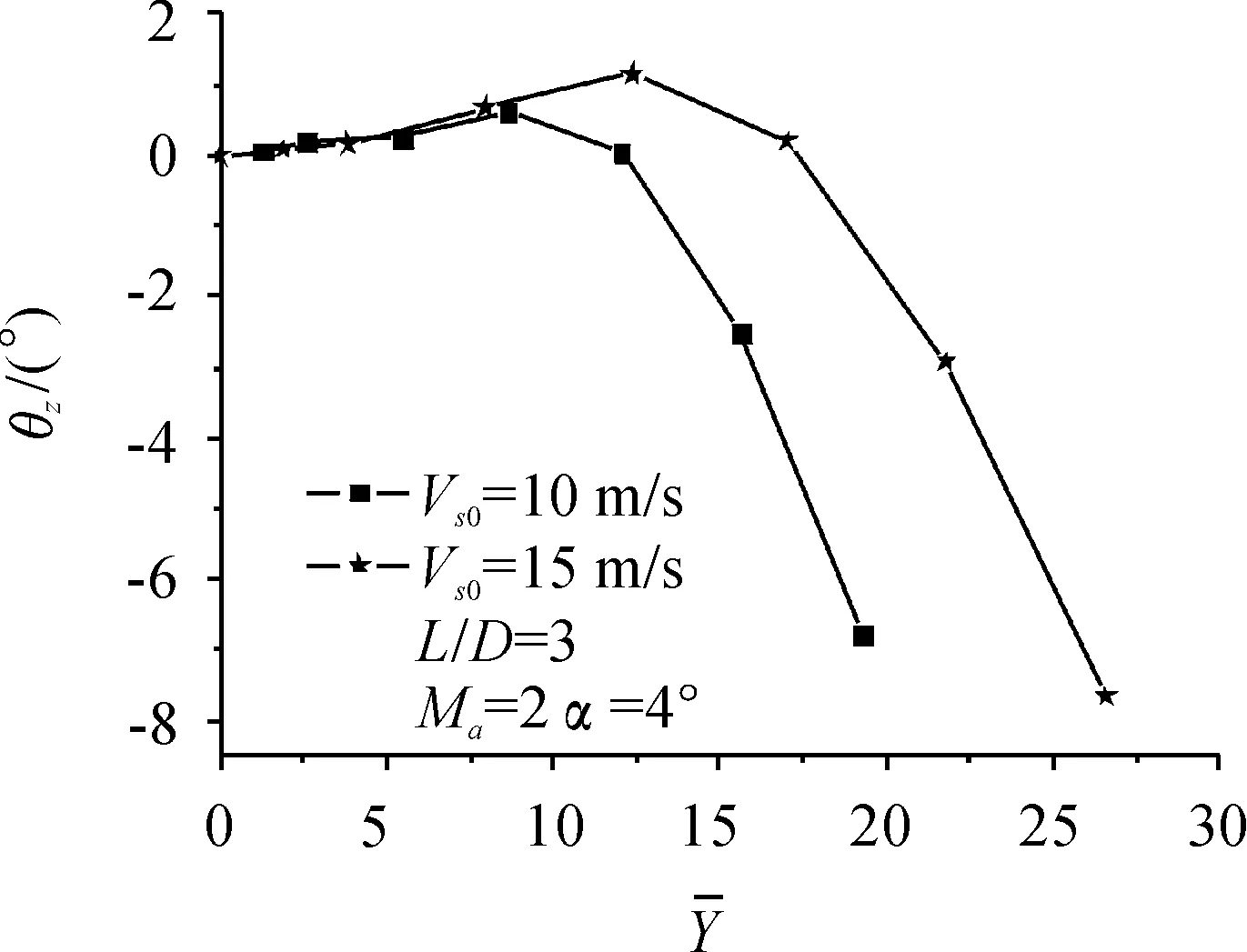
图17 姿态角随时间变化曲线

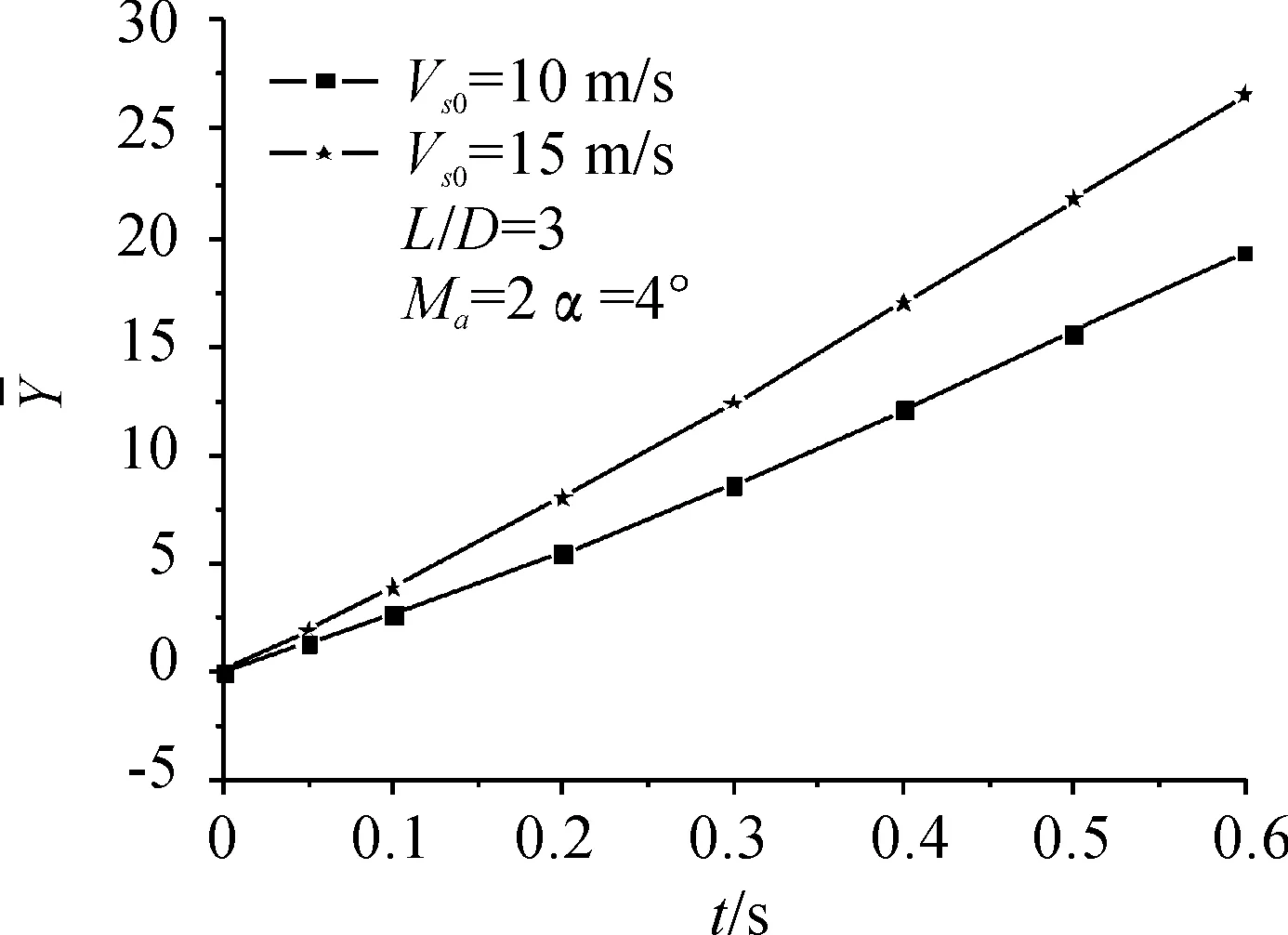
图18 机弹垂向间距随时间变化曲线

从图17可以看出，在分离的过程中，初始速度为Vs0=15 m/s的情况下航弹的姿态角随时间的变化与初始速度为Vs0=10 m/s时航弹的姿态角随时间的变化基本一致。从图18可看出，航弹下落到一定距离所用的时间，初始速度为Vs0=15 m/s的比初始速度为Vs0=10 m/s的明显短，即初始下抛速度越大，离开载机干扰区的时间就越短。

综上所述，航弹的初始下抛速度决定了机弹分离时间的长短和分离过程中航弹姿态的变化。初始下抛速度越大，机弹分离的时间就越短，航弹姿态角变化越小，有利于分离过程中航弹姿态的稳定，从而有利于机弹安全分离。反之，初始下抛速度越小，航弹姿态角变化越大，不利于分离过程中航弹姿态的稳定，甚至会出现航弹翻转或撞击载机的危险。

3.4 非定常分离轨迹图

图19显示的是来流马赫数为Ma=2，来流攻角为α=2°，航弹初始下抛速度为Vs0=10 m/s，长深比L/D=3的武器舱抛撒航弹时机弹分离过程中航弹的运动轨迹。从图19中看出随着时间的推移，航弹下落得更快，且向后移动的位移量越来越大，航弹姿态变化越来越大。

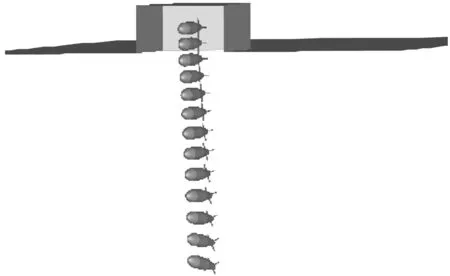
图19 Ma=2、α=2°、Vs0=10 m/s时机弹分离过程中航弹的运动轨迹

4 结论

1) 内埋式航弹与载机的分离时，弹舱空腔对航弹与载机的分离流场有很大影响，特别是分离初期，当航弹还位于弹舱内部和弹舱附近时，影响尤其严重。

2) 航弹的初始下抛速度决定了机弹分离时间的长短和分离过程中航弹姿态的变化。初始下抛速度越大，机弹分离的时间就越短，航弹姿态角变化越小，有利于分离过程中航弹姿态的稳定，从而有利于机弹安全分离。反之，初始下抛速度越小，航弹姿态角变化越大，不利于分离过程中航弹姿态的稳定。