基于事故树的弹药方舱防护需求分析

宣兆龙，李天鹏，刘亚超

(1.陆军工程大学石家庄校区， 石家庄 050003； 2.陆军炮兵防空兵学院， 郑州 450000)

弹药作为武器装备重要的组成部分，具有特殊的社会属性和技术属性，使得弹药保障相对于其他物资的保障具有更多的储运要求，这些要求贯穿于弹药保障的各个环节。弹药方舱作为一种新型弹药集装单元，综合运用了托盘、集装箱和方舱技术[1]，是未来弹药保障系统的重要形式。

事故树分析是通过从结果到原因的逻辑树推理及图形演绎，对可能造成系统事故的各种因素进行层层分析的一种方法，用于揭示导致事故发生的直接、间接原因，并寻求防止结果发生的防范措施[2]。本文采用事故树分析法，以弹药保障任务失败为弹药保障系统事故树的顶事件，研究弹药保障系统中火灾、爆炸和弹药技术损伤等3类事故事件，利用逻辑或门将顶事件与这3类事故事件相连接，通过对每个事故事件建立逻辑模型，研究分析整个弹药保障系统的诱发因素，可以有效指导弹药方舱的防护设计工作。

1 事故树分析法

事故树分析法是在20世纪60年代由美国贝尔实验室基于图论提出的一种安全评价方法，是一种表示导致灾害事故有关的各种因素之间因果关系和逻辑关系的分析法[3]。事故树分析主要是针对既定系统可能出现的事故条件，以及可能导致的灾害后果，按流程的先后次序和事故发生原因的各种因果关系绘制成程序方框图，也就是画出表示导致灾害事故的各种因素之间的逻辑关系图；根据这种逻辑关系图分析系统的安全问题或系统的运行问题，进而针对各因素制定防范措施[4]。

事故树是一种逻辑图模型，不能够采用数学方法进行分析，更不能有效说明基本事件之间的关系。而研究分析基本事件之间的关系，是改善系统，防止事故发生的关键。为了进一步研究基本事件之间的关系，必须把图形模型转换成数学表达式，也就是所谓的数学模型。事故树的数学模型基本组成单元为逻辑乘积与逻辑和。其中，逻辑乘积对应的逻辑关系是与门；逻辑和对应的逻辑关系是或门。下面将针对图1所示的事故树模型，对事故树模型的转化和化简进行系统地阐述。

事故树模型转化为数学模型的方法一般有自下而上法和自上而下法。这里主要介绍自上而下法。自上而下的转化方法一般自顶事件开始，根据事件间的逻辑关系，层层向下推进，直至最后全部用基本事件表示顶事件为止，得到事故数模型的数学表达式。

首先，给事故树模型中的事件进行编号，如图1所示。

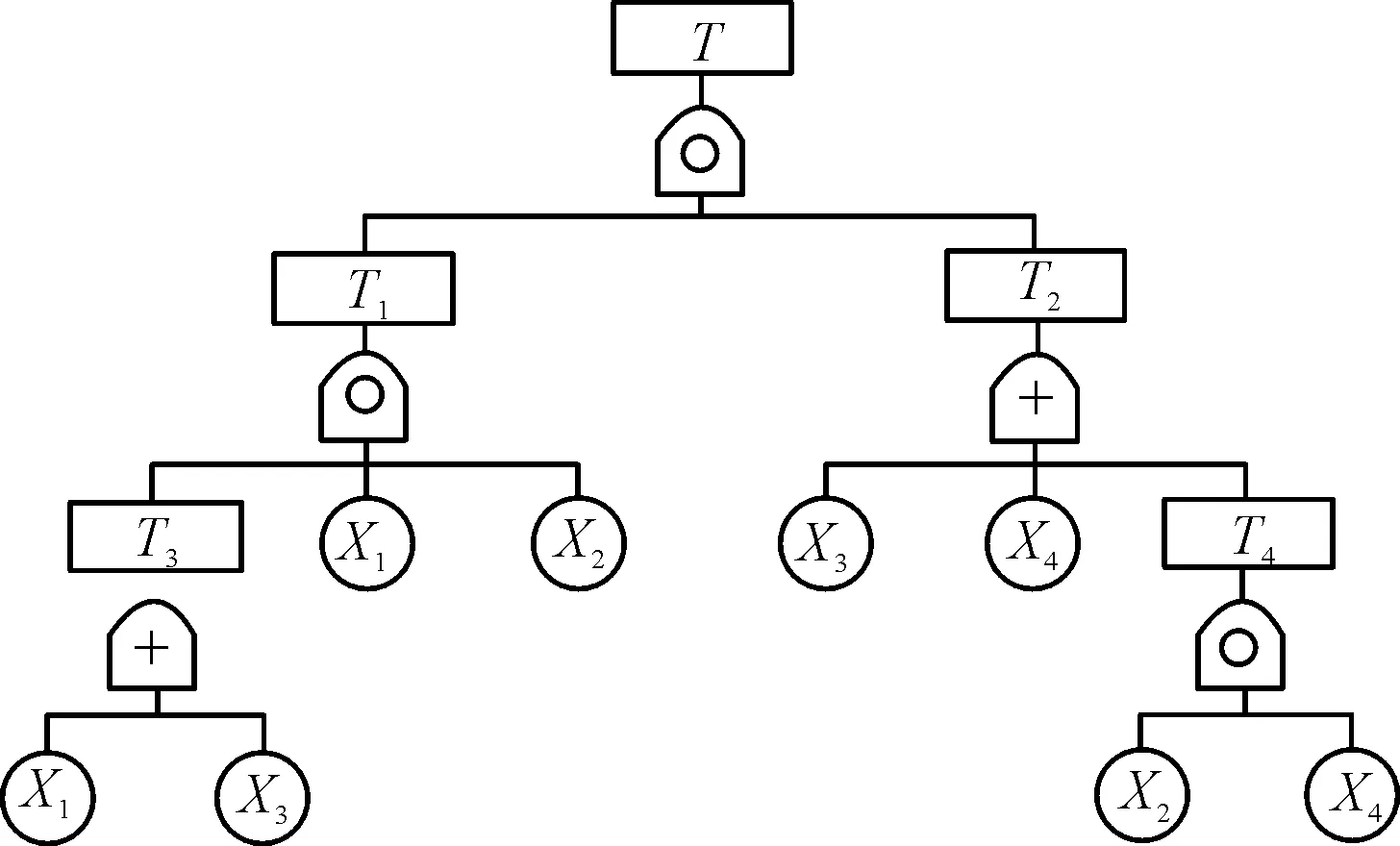
图1 事故树模型

由事故树模型首先得到：

T=T1T2

其中，T1=T3X1X2，T2=T4+X3+X4。

然后得到

T=T3X1X2(T4+X3+X4)

又因

T3=X1+X3，T4=X2X4

最后得到

T=(X1+X3)X1X2(X2X4+X3+X4)

(1)

由此可见，将事故树模型转化成数学模型后，数学关系式也很复杂，无法说明基本事件之间的关系。这就需要对事故树的数学表达式进行整理，以便于在后续的分析工作中，获得较理想的结果。

对事故树的数学表达式进行整理的过程成为数学表达式的化简。化简的方法一般采用布尔代数运算法则。以A、B、C、D分别表示四个集合，A′、B′、C′、D′分别表示对应集合的补集，其化简公式主要有：

AB+AB′=A，A+AB=A，A+A′B=A+B，

AB+A′CD+BCD=AB+A′CD

(AB+A′C)′=AB′+A′C′

因此，式(1)可化简为

T=X1X2X4+X1X2X3

(2)

或者

T=X1X2(X4+X3)

(3)

采用事故树分析方法研究弹药保障系统事故的最终目的是分析如何避免事故事件的发生。显然，若事故树图模型中所有的基本事件都不发生，则顶事件肯定不会发生，这些基本事件的集合称为径集。实际上，分析径集没有研究意义。在弹药保障系统中，最关心的是分析、控制那些关键因素，事故就不会发生，所以只需要研究最小径集。最小径集为不发生顶事件时，至少需要那些基本事件不发生的集合。式(3)中{X1}，{X2}，{X3，X4}即为事故树的3个最小径集。

分析可知，只要控制基本事件X1，X2的发生，就可以有效避免顶事件的发生；同时控制X3与X4不发生，也可以控制顶事件不发生；控制基本事件X3或X4不发生则可以很大程度的减少顶事件发生的概率。

2 火灾事故分析

无论是平时还是战时，火灾都是弹药保障系统特别是弹药储存保管环节重点防范的事故事件之一。该事故事件的发生势必会导致弹药的技术损伤及断供事件的发生，而且很可能会诱使爆炸事件的发生。不仅会严重影响弹药保障工作的顺利进行，还会给部队和国家带来重大的经济损失与人员伤亡。根据火灾事故分析，建立弹药保障系统的火灾事故树[5]，如图2所示。

图2 弹药保障系统的火灾事故树

图2中，T1表示火灾，为该事故图中的顶事件；T2，T3，T4，T5，T6，T7及T8分别依次表示库内火灾、库外火灾、可燃物、火种、自燃、库内火花及机械应力，为该事故树的中间事件；X1，X2，X3，X4，X5，X6，X7，X8及X9分别依次表示木质包装、装药分解、库内明火、静电、雷击、高温、摩擦、跌落与振动，为该事故树的基本事件。

根据弹药保障系统火灾事故树图，采用自上而下的方式，将该逻辑模型转化为数学模型，其化简结果为

T1=(X1+X2+X4+X5+X7+X8+X9)·

(X2+X3+X4+X5+X7+X8+X9)·

(X3+X4+X5+X6+X7+X8+X9)

(4)

由式(4)可知，弹药保障系统火灾事故树的最小径集为{X1，X2，X4，X5，X7，X8，X9}，{X2，X3，X4，X5，X7，X8，X9}，{X3，X4，X5，X6，X7，X8，X9}。由最小径集定义可知，只需控制3个事件集合中的其中一个集合内的事件均不发生，即可有效防止弹药保障系统火灾事故。

3 爆炸事故分析

爆炸事件往往会给部队造成重大损失，严重影响部队的作战能力。因此爆炸也是弹药保障系统，特别是在对弹药进行装卸、运输等作业时重点防范的事故事件之一。根据爆炸事故分析，建立弹药保障系统的爆炸事故树图[6]，如图3。

图3 弹药保障系统的爆炸事故树

图3中，T9表示爆炸事件，为该事故树的顶事件；T10，T11，T12，T13，T14分别表示库内爆炸、库外爆炸、包装破损、运输冲击及腐蚀；其他编号与上述表示意义相同。

根据弹药保障系统爆炸事故树图，采用自上而下的转换方法，将事故树模型转化为数学模型，其化简结果为

T9=(X4+X5+X8+X9+X10+X11+

X12+X13+X14+X15)·

(X4+X5+X7+X8+X9)

(5)

由式(5)可知，弹药保障系统爆炸事故树的最小径集为{X4，X5，X8，X9，X10，X11，X12，X13，X14，X15}，{X4，X5，X7，X8，X9}，即若防止弹药保障系统爆炸事件的发生，只需控制其中任何一个最小径集中的所有基本事件不发生。

4 弹药技术损伤事故分析

弹药的技术损伤是指影响弹药作战效能的结构或者功能元件的变化，它也是弹药保障系统重点防范的事故事件之一。根据弹药技术损伤事故分析，建立弹药保障系统的技术损伤事故树图[7]，如图4。

图4 弹药保障系统的弹药技术损伤事故树

图4中，T15表示弹药的技术损伤事件，为该事故树的顶事件；T16表示环境应力；X10，X11，X12，X13，X14，X15分别表示高温、低温、高湿、盐雾、沙尘及淋雨；其他编号与上述表示意义相同。

根据弹药保障系统弹药技术损伤事故树图，采用自上而下的转换方法，将事故树模型转化为数学模型，其化简结果如下。

T14=(X8+X9+X10+X11+X12+X13+X14+X15)

(6)

由式(6)可知，弹药保障系统的弹药技术损伤事故树的最小径集为{X8，X9，X10，X11，X12，X13，X14，X15}。

针对弹药保障系统中火灾、爆炸和弹药技术损伤3类事故事件，其基本事件有15种之多[8]。通过分析发现，这3类事故事件具有许多相同的诱发因素，为进一步明确弹药保障系统事故事件的诱发因素之间的关系，将3类事件的数学表达式进行化简，结果如下：

T=(X8+X9+X10+X11+X12+X13+X14+X15)

(7)

由式(7)可知，只要同时降低跌落、振动等8类基本事件的发生概率，就可有效降低弹药保障系统火灾、爆炸和弹药技术损伤等3类事故事件发生的概率，使部队可以快速、准确、有效的完成弹药保障任务。

上述8类基本事件中的高温、低温、高湿、盐雾、沙尘、淋雨均是弹药保障系统的气候环境因素，是不可改变的基本事件。若要防止此类基本事件诱发弹药保障系统的事故事件，只能通过截断影响途径的方式，即在弹药方舱的结构设计中加入相关防护功能，为弹药储存提供一个稳定的环境条件。跌落和振动是弹药保障系统的力学环境因素，长时间的振动激励会给弹药造成损伤[9-10]。因为弹药保障系统的运行离不开装卸和运输作业，所以这两个力学环境因素也是弹药保障系统不可避免的基本事件。为防止跌落和振动事件诱发弹药保障系统事故事件的发生，只能通过增加弹药方舱的结构强度和衰减能量传递的方式，避免方舱结构损伤，保证弹药方舱内部环境的稳定性。因此，为了避免弹药保障系统事故事件的发生，弹药方舱必须要针对高温、低温、高湿、淋雨、盐雾、沙尘、跌落、振动等8类环境条件进行相应的防护功能设计。其中高温、低温要求弹药方舱具备良好的保温和密封性能；高湿、淋雨要求弹药方舱具备较好地密封条件；盐雾、沙尘要求弹药方舱具备较强的防腐蚀能力；跌落与振动要求弹药方舱具备抗冲击和减振的能力。

5 结论

弹药方舱必须要具有保温、密封、防腐蚀和抗冲击减振等防护功能，保证其内部环境的稳定性，为弹药提供一个适于储存的环境条件，才能有效降低弹药保障系统事故事件的发生概率。