基于涡流检测的轨道炮沉积层厚度测试仿真

向红军，王俊晓,2，郝雁军，鲁 飞，肖 静

(1.陆军工程大学， 石家庄 050003； 2. 73146部队, 福建 泉州 362000;3.北京军事代表局， 北京 100000; 4.陆军第81集团军， 河北 张家口 075000)

电磁轨道炮由于具有初速精确可控、高初速、超远程打击等优点，在远程火力支援、火力压制、临近空间攻防等方面具有广阔的应用前景，是当前各国研究的热点[1-2]。轨道炮从提出到现在已经过去半个多世纪，但是仍然处于工程样机研制阶段，没有走向战场，主要是因为其电源小型化和集成技术、轨道寿命技术、超远程一体化弹药技术等关键技术还没有完全攻克，制约了其工程化研制进程。轨道在发射铝质电枢时，由于轨道和电枢界面之间的高速滑动电接触，在欧姆热、摩擦热和冲击电流等作用下，铝质电枢和轨道的接触面会出现熔蚀，大大降低摩擦阻力，并在轨道表面产生沉积，形成类似电镀效应的沉积层[3-6]。在重复发射时，沉积层将对发射轨道的寿命和发射性能产生影响。为此，分析轨道炮重复发射轨道的沉积层特性，对研究电磁轨道的寿命和重复发射性能具有非常重要的作用。沉积层厚度测量是分析其特性的重要环节。

传统的厚度测量方法有很多，包括接触式测量和非接触式测量。接触式测量容易造成轨道表面的损伤和污染；非接触式测量包括电磁超声测厚、激光测厚和射线测厚等[7]。由于沉积层厚度大约在微米级，而电磁超声测厚由于其自身的测量盲区，很难对涂敷薄层进行厚度测量。因此，利用电磁超声测厚技术难以满足使用要求。激光测厚的成本较高、系统复杂；射线测厚又存在射线源，对安全要求高。因此，上述方法均不适用于轨道沉积层厚度的测量。

涡流检测具有灵敏度高，操作使用方便的特点，非常适合用于涂敷表面和金属薄板厚度的测量[8]。为此，本研究将基于涡流检测技术，对沉积层的厚度进行测量，构建相应的仿真模型，分析不同参数下的测试性能，为沉积层厚度的测量提供有效的方法手段。

1 涡流测厚工作原理

涡流测厚的工作原理如图1所示。涡流测厚探头主要由检测线圈、激励线圈、铁芯等构成。当在激励线圈中通入正弦交流电流时，激励线圈将产生激励磁场[9-10]。根据电磁感应定律可知，激励磁场将在铝沉积层和铜轨道上感应出涡流。涡流产生涡流场。由于沉积层和铜轨道电导率不同，使得该涡流场与无沉积层时的涡流场存在一定的差异。该涡流场被检测线圈接收后，在接收线圈两端产生感应电压，该感应电压包含了沉积层的厚度信息。通过分析该感应电压，即可得到沉积层的厚度。

2 沉积层厚度检测有限元模型

通过建立基于涡流的沉积层厚度检测有限元模型，分析不同参数下的沉积层厚度检测性能，不断提高涡流检测探头的灵敏度。

2.1 几何模型构建

根据涡流检测沉积层厚度的工作原理可知，其仿真分析涉及磁场和涡流的分析计算，因此可以选择Comsol Multi-physics中的Magnetic Fields磁场模块进行仿真计算，求解器选择频域求解器。

涡流检测探头为轴对称模型，如图1。为此，为提高仿真效率，可以建立涡流检测探头的二维轴对称模型。基于Comsol Multi-physics建立的沉积层厚度检测有限元几何模型如图2所示。其中，各部分的尺寸如下：磁芯的直径为20 mm，高度为50 mm；检测线圈的内径为20 mm，外径为50mm，高度为50 mm，匝数位1 400匝；激励线圈的内径为50 mm，外径为70 mm，高度为50 mm，匝数为1 000匝；金属铜轨道的直径为200 mm，高度为40 mm，其中沉积层高度为10 μm；涡流探头和待测金属轨道之间的距离为1 mm；根据磁场仿真需要，设置的空气域直径为400 mm，高度为200 mm。

图1 涡流测厚工作原理

图2 有限元几何模型

2.2 材料添加

图2中，需要对不同的域赋予不同的材料属性。其中空气域的材料设置为空气，为了提高计算模型的收敛性，将其电导率设置为1 S/m，其余各材料属性参数的设置如表1所示。表1中，σ为材料的电导率，μr为材料的相对磁导率，εr为相对介电常数。

表1 材料属性参数

2.3 物理场设置

整个模型的边界条件设定为狄利克莱边界条件，即边界上磁矢势为0。此外 ，由于所选模型为二维轴对称模型，在对称面上会设置对称边界条件。磁场设置中，将激励线圈和检测线圈均设为均匀多匝线圈，其中激励线圈的激励源设为电流0.56 A，检测线圈的激励源设为电流0 A，表明检测线圈为开路。两种线圈的线径均设为直径0.5 mm。

2.4 网格剖分

由于需要关注的是待测轨道和沉积层中的涡流，因此需要对沉积层和轨道的网格进行细化。设置沉积层网格的最大尺寸为8 μm，轨道的网格最大尺寸为1 mm，剖分后的网格如图3所示。

图3 网格剖分

2.5 求解与计算

在求解器参数设置中，设置求解频率分别为100 Hz、600 Hz、1 100 Hz和1 600 Hz，然后进行求解计算，从而得到不同频率下待测轨道和沉积层中的涡流分布，以及检测线圈的输出电压。其中频率为1 100 Hz时，待测轨道和沉积层中的涡流密度分布如图4所示。从图4可以看出，铜轨道中的涡流密度大约为-4.5×106A/mm2，沉积层中的涡流密度大约为-1×106A/mm2。

图4 涡流密度分布

同时，通过仿真，得到不同激励频率下，检测线圈的感应电压的幅值如图5所示。从图5可以看出，随着频率的升高，检测线圈中的电压幅值逐渐增大，有利于沉积层厚度的检测。

3 不同参数对涡流探头性能的影响

在利用涡流探头测量厚度时，通常利用差分法来减小测量误差。将检测探头得到的幅值电压信号与标准轨道测得的幅值电压信号的差值作为探头输出信号，并对不同参数情况下的仿真模型进行仿真计算。

3.1 不同激励频率对探头性能的影响

利用上述仿真模型，对不同沉积层厚度、不同激励频率下的沉积层进行仿真分析，得到的电压幅值信号差分曲线和相位差信号曲线如图6、图7所示。

图5 电压幅值曲线

图6 差分幅值电压曲线

图7 相位差曲线

从图6和图7可以看出，相同频率下，沉积层厚度越大，输出的幅值电压信号越大，但是相位差变化不大。因此，可以选择幅值电压的差分信号作为沉积层厚度的检测信号。根据幅值电压信号的差值，即可计算得出沉积层厚度。

同时，从图6还可以看出，在相同厚度下，随着频率的增大，输出电压的幅值越大。因此，适当增大激励频率，可以提高涡流探头对沉积层厚度检测的灵敏度。

3.2 不同提离距离对探头性能的影响

为了避免对轨道表面造成损伤，涡流探头和轨道之间是一种非接触式测量。此时探头和轨道之间的距离也会对测量结果产生影响。从模型可知，上述仿真是在提离距离为1 mm时进行的。下面利用上述仿真模型，对探头的提离距离进行仿真计算，其中沉积层厚度为10 μm。通过仿真，得到不同频率和不同提离距离下的结果如图8所示。

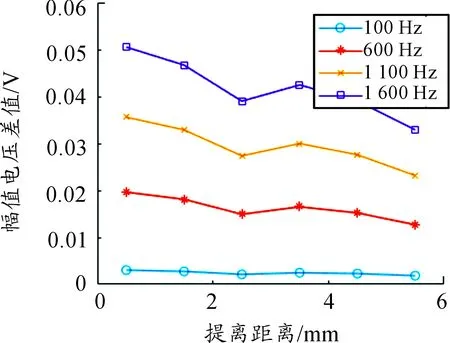
图8 差分幅值电压曲线

从图8可以看出，随着提离距离的增大，涡流探头幅值电压的差值先减小然后小幅增大，最后再快速减小。因此，从总体变化趋势看，较小的提离距离有利于提高涡流探头的灵敏度。

3.3 铁芯对涡流探头性能的影响

铁芯会增加耦合磁场的强度，为分析铁芯对涡流探头的影响。在沉积层厚度为10 μm，激励频率为1 600 Hz时，对有无铁芯两种情况下的模型进行了仿真计算，得到涡流探头的幅值电压差值如图9所示。

从图9可以看出，在涡流检测探头中增加铁芯时，幅值电压差值随着沉积层厚度的变化趋势更快，曲线具有更高的斜率。因此，铁芯可以增加涡流探头的灵敏度，从而提高涡流探头的测试性能。

图9 有无铁芯时的差分幅值电压曲线

3.4 不同线圈高度对探头性能的影响

在激励线圈和检测线圈的半径保持不变的情况下，通过改变两线圈的高度，则线圈的匝数也会发生相应变化。虽然线圈高度变大、匝数增多会增大线圈和待测轨道之间的磁场耦合程度，但是匝数增多也会导致线圈电阻的变大，影响激励线圈中的电流。为此，需要分析线圈的高度或匝数对探头性能的影响。根据图2建立的仿真模型可知，在线圈内外径和导线截面保持不变的情况下，激励线圈高度h1和其匝数N1之间的关系为

N1=h1/50×1 000

(1)

同理，检测线圈高度h2和其匝数N2之间的关系可以表示为：

N2=h2/50×1 400

(2)

在激励线圈和检测线圈高度保持一致的情况下，利用上述仿真模型进行计算，得到仿真结果如图10所示。

图10 差分幅值电压曲线

从图10可以看出，随着线圈高度的增大，差分幅值电压先不断增大，然后逐渐趋于平缓，其理想的线圈高度大约为55 mm。因此，对于涡流探头来说，存在最佳的线圈高度，使其差分幅值电压达到最大值。

4 结论

通过对基于涡流检测技术的沉积层厚度测试的仿真分析，可以看出：随着沉积层厚度的增加，涡流探头的差分幅值信号逐渐增大，因此，利用涡流检测技术，能够实现沉积层厚度的测量。同时，随着激励频率的增大、提离距离的减小和铁芯的增加，涡流探头的灵敏度会增大；此外，线圈存在最佳的高度，可使涡流探头得到最大的差分幅值。因此，要提高涡流探头对沉积厚度的测试效果，可以适当增大激励频率、减小提离距离并增加铁芯，选择最佳的线圈高度。