大弯曲弹道捷联导引头制导律研究

李 菁,张 雷，胡俊香

(1.安徽神剑科技股份有限公司， 合肥 230000； 2 陆军南京军代局， 南京 210024)

现代战争是高技术战争，精确制导武器是决定现代战争胜负的关键因素。捷联式激光导引头因其技术成熟、低成本、抗过载性能良好等特点，多用于精确打击弹药。捷联式导引头可根据探测到的激光光斑位置信息，可为弹上控制系统提供准确的弹目偏差量信息(含弹目偏差量R、自转角θ)[1-7]。如国内已装备的激光制导类弹药多为平射直瞄类弹药，在采用的弹体追踪制导律中，根据导引头的光斑位置信息，可确定具体的修正方位[8-10]。图1表示了导引头输出弹目偏差量在弹体坐标系上的情况。

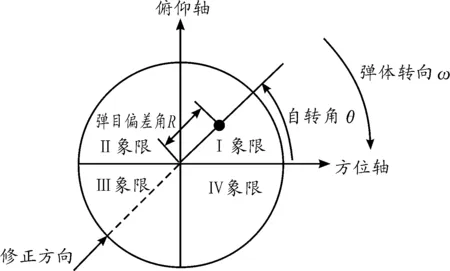
图1 导引头输出弹目偏差量在弹体坐标系上的情况示意图

1 迫弹弹道特性分析

常用于山地作战的迫弹平台，以45°～80°大射角射击，全弹道为典型大弯曲弹道全装药条件下全弹道曲线见图2。

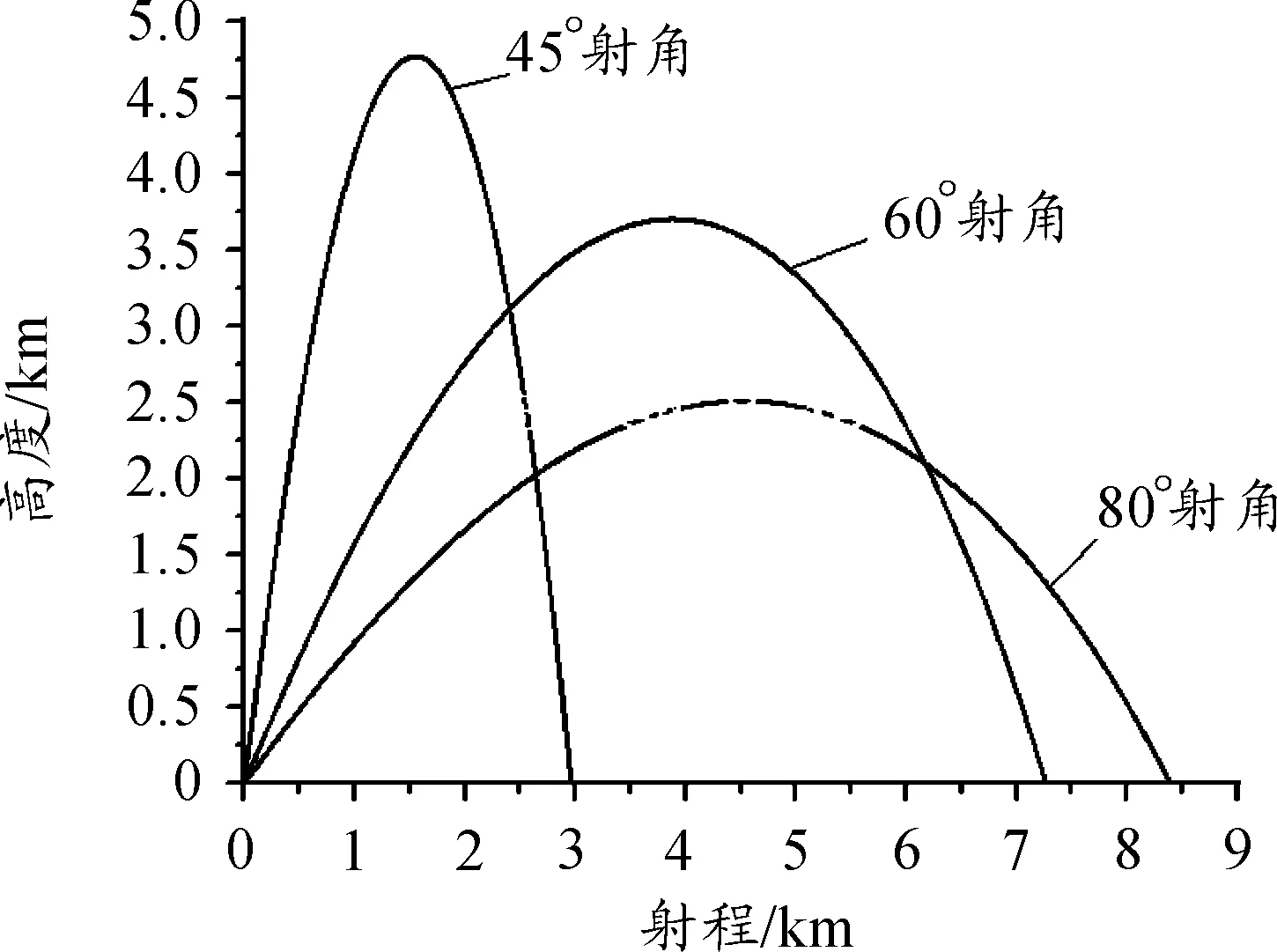
图2 全装药条件下全弹道曲线

弹道的弯曲特性及导引头的捷联式固定方式决定了弹丸沿标准弹道(无需修正即可命中目标的理想弹道)飞行的情况下也存在随弹道倾角变化的固有弹目偏差角，标准弹道下弹目偏差角R与弹道倾角随时间的变化见图3。

由于存在弹道固有的弹目，按照图1根据导引头光斑信息确定修正方向将会带来较大的偏差，弯曲弹道特性决定了导引头光斑变化规律不同于平射直瞄类位置平台变化规律，受重力影响而无法直接获得弹目相对位置关系，如仍按照图1进行控制决策，将导致修正偏差较大，不足以保证修正精度的实现，常规的弹体追踪制导律控制方式已不能适用于迫弹平台。因此对捷联式激光导引头在迫弹平台上的光斑变化规律进行分析研究，是迫弹平台制导类产品控制方案制定、算法设计的基础。

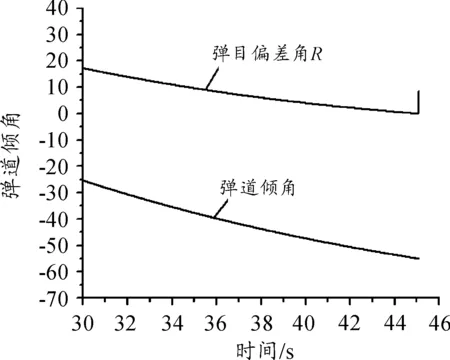
图3 标准弹道下弹目偏差角R与弹道倾角与时间的关系

2 弹道解算模型建立

根据迫弹弹道特性，建立弹道解算模型为：

其中：V为存速；c为平均弹道系数；Cx0(Ma)为43年阻力定律；θ为弹道倾角；g为重力加速度；L为弹目距；R为理论弹目偏差角；X0为射程；Δy为炮目高程差。激光光斑位置信息的坐标转化模型如图4所示。

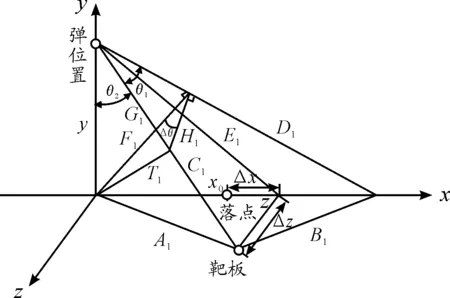
图4 激光光斑位置信息的坐标转化模型

弹丸转速为ω，惯导组件实测重力方向夹角为θ。已知目标靶板与落点间的位置：Δx=X靶-X0，Δz=Z靶-Z0，导引头实测光斑位置信息：弹目偏差角R′=θ1、θ′=θg+Δθ。

3 激光光斑变化规律分析

根据仿真计算可知，当弹道预测落点在目标前方偏左方时，光斑相对重力方向变化规律示意图如图5(近10侧10代表弹丸落点落于目标左前方位置，纵向射程差为10 m，横向距离差为10 m)，当弹道预测落点在目标后方偏左方时，光斑相对重力方向变化规律示意图如图6所示(远10侧20代表弹丸落点落于目标左后方置，纵向射程差为-10 m，横向距离差为20 m)。

4 激光光斑变化规律在弹体追踪制导律中的运用

考虑重力影响，修正方向应为实测光斑与理论弹道光斑的连线方向，考虑导引头光斑变化规律后修正方向在弹体坐标系上的示意图如图7。通过蒙特卡洛打靶法进行对比仿真分析，考虑修正弹道对导引头变化规律的影响量，图8表示了蒙特卡洛仿真结果从图8和表1(未考虑导引头光斑变化规律的修正仿真结果，考虑导引头光斑变化规律的修正仿真结果)仿真结果，考虑重力影响，将导引头光斑变化规律运用至制导律设计方案中，可有效抑制因修正方向偏差引起的弹丸离群现象，从而提高CEP修正精度。

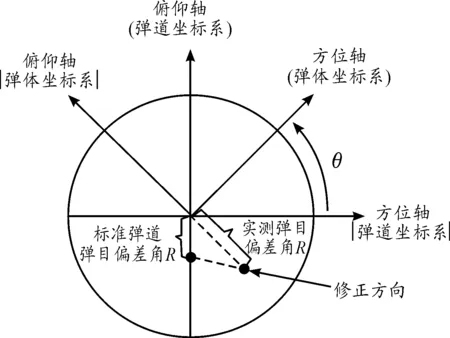
图7 考虑导引头光斑变化规律后修正方向在弹体坐标系上的示意图

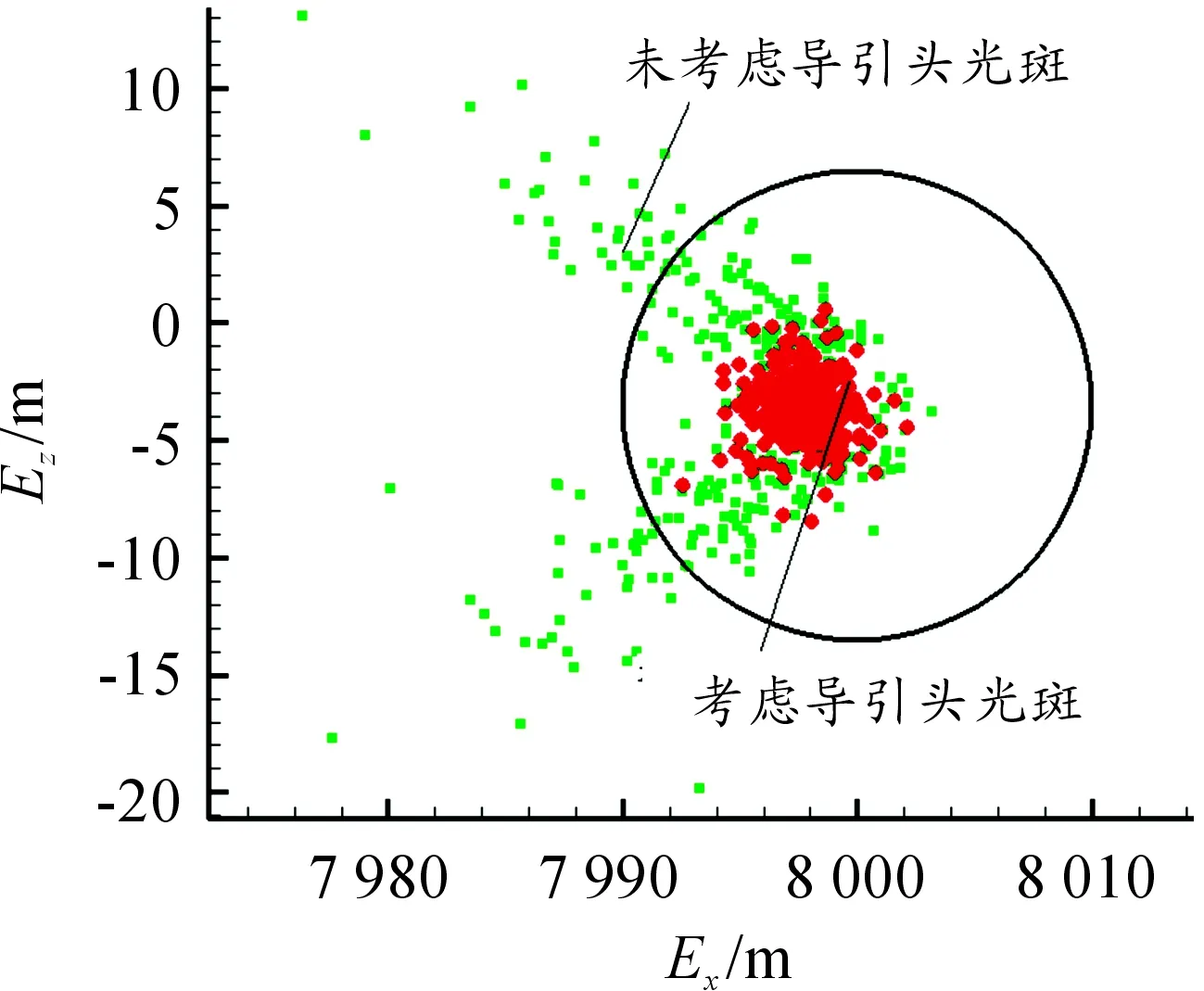
图8 蒙特卡洛仿真结果

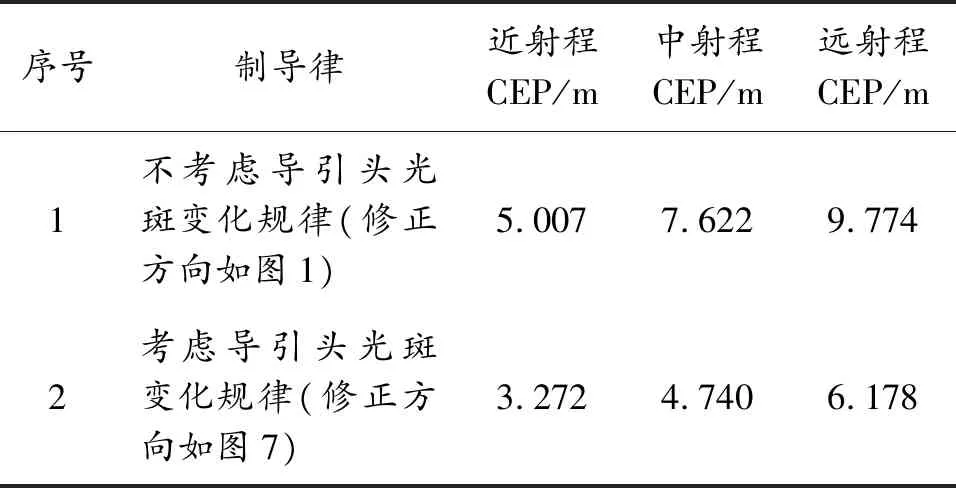
序号制导律近射程CEP/m中射程CEP/m远射程CEP/m1不考虑导引头光斑变化规律(修正方向如图1)5.0077.6229.7742考虑导引头光斑变化规律(修正方向如图7)3.2724.7406.178

5 结论

将捷联式激光导引头在弹道末端修正段的探测光斑变化规律运用至制导律中，可有利提高弹药的修正精度，提升迫弹平台的攻击效能。