基于自适应网格的急流条件下污染物输运高效高精度模拟

曹 引，冶运涛，梁犁丽，赵红莉，蒋云钟，王 浩

（1.东华大学 环境科学与工程学院，上海 201620；2.中国水利水电科学研究院 水资源研究所，北京 100038）

1 研究背景

近年来，突发水污染事件频发，导致局部水域水质恶化，严重威胁周围及下游区域居民的用水安全，同时会造成巨大的经济损失和严重的生态环境问题［1］。突发水污染事件的影响范围和水流条件密切相关，如果在暴雨洪水和溃坝水流等急流条件下突发水污染事件，释放的污染物将随着急速演进的洪水快速运移和扩散，导致水质在短时间内迅速恶化，可能造成自来水厂停水和工业停产等问题，威胁下游居民的用水安全，极易引发社会恐慌［2］。

水污染事件突发后，需要了解污染物在水体中的运移和扩散规律，及时判断突发水污染事件的危害范围和持续时间，以助于快速评估突发水污染事件的危害并及时预警［3-4］。水动力水质模型是评估突发水污染事件危害程度的有效手段，在突发水污染事件管理中得到有效应用［5］。陶亚等［6-7］分别采用基于有限差分方法的平面二维水动力水质模型和EFDC水动力及污染物模型预测了河流突发水污染事故后下游城市的应急响应时间，模拟了不同应对措施的处理效果；饶清华等［8］基于有限元法构建了模拟闽江下游突发水污染事件中污染物迁移扩散的水动力及水质模型，定量模拟了污染物的时空分布；Dong等［9］将基于有限体积法的MIKE21模型用于突发水污染事件的风险分析，模拟了沿海河流和近岸海域化学污染物输移扩散过程。目前研究多集中于缓流条件下突发水污染事件中污染物的输运模拟，准确模拟暴雨洪水和溃坝洪水等急流条件下污染物的输运规律充满了挑战［5］:（1）突发水污染事件的地点和时间的随机性，需要快速获取水污染事件发生区域的地形、初始条件和出入流边界条件，为水质模型提供建模数据；（2）洪水演进过程中会产生激波和动态变化的干湿边界，模型需要能够有效捕捉激波和模拟干湿边界；（3）实际应用中水流常流经复杂地形区域，如山谷、河流和城市区域等，模型必须能够有效描述复杂的地形条件；（4）突发水污染事件危害评估和预警要求很高的时效性，模型必须具有很高的计算效率。水质模型构建所需的地形条件可以通过SRTM 30米DEM数据、历史地形观测数据、人工测量和插值等方式快速获取；初始条件和出入流边界可以通过上下游水文站、水质在线监测站或者便携式水质分析仪测量获取。水质模型构建后，求解模型控制方程获得稳定和谐的数值解是应用水动力水质模型模拟污染物输运过程的关键，相比于有限元法和有限差分方法，Godunov有限体积法由于可以有效捕捉急流条件下突发水污染事件中产生的激波间断和污染物浓度间断［10］，适合急流条件下污染物的输运模拟［11］。水动力水质模型利用网格离散计算区域，结构网格和非结构网格是水动力水质模型最常用的网格类型。非结构网格对复杂地形和边界具有较强的拟合能力，但生成过程复杂［12］；结构网格生成简单，但对复杂地形的拟合能力较差，为了提升模型模拟精度，必须增加网格数量，这势必会降低模型计算效率。基于结构网格的自适应网格技术可以根据水流特性和污染物浓度分布自适应调整网格大小，保证模型模拟精度的前提下可以明显提升模型计算效率［5，13］。

本文基于自适应结构网格构建了适用于复杂地形和急流条件下突发水污染事件中污染物输运模拟的二维水流-输运耦合模型，模型采用能够有效捕捉激波的Godunov有限体积法离散二维水流-输运控制方程，利用具有时空二阶精度的MUSCL-Hancock方法求解，界面通量采用HLLC近似黎曼求解器求解，为了保证干湿边界处模型的稳定性和守恒性，采用非负重构技术［11］和局部底部高程修正方法［13］重构界面两侧黎曼变量。最后分别利用水槽试验、物理模型和实际算例检验了模型模拟突发水污染事件中污染物输移的精度和稳定性。

2 自适应网格生成技术

本文采用的自适应网格为递归的层次结构网格（图1），叶网格（如网格（i，j）和（i，j+1））划分层级lev为0，网格最大划分层级为div_max，叶网格大小为Δx0和Δy0。对叶网格进行细化可以得到子网格，子网格大小为Δx=Δx0/2lev，Δy=Δy0/2lev。任何网格和其邻居网格大小必须满足2倍关系，即网格大小必须是其邻居网格大小的2倍、1倍和1/2倍（2∶1准则），该过程需要存储邻居网格信息，为了减少存储要求，邻居网格信息采用网格之间的相对关系来确定［14］。自适应网格可以快速生成，具体生成步骤如下:

（1）生成能覆盖计算域的叶网格（i，j），i=1，2，…，M，j=1，2，…，N，M和N分别为x和y方向上的网格数，设置叶网格划分层级为0，即lev（i，j）=0；

（2）根据研究区边界种子点识别参与计算的网格单元；

（3）依次计算内部网格单元（i，j，is，js）（图1）的水位梯度（gradη）和污染物守恒浓度梯度（gradqc）（式（1）—式（4）），取两者最大值gradΦ=max（gradη，gradqc）作为该网格划分层级的判定梯度；

（4）如果gradΦ大于网格划分阈值Φsub，或者网格（i，j，is，js）位于干湿边界处，设置叶网格的划分层级为lev（i，j）=lev（i，j）+1，如果lev（i，j）=div_max，则保持lev（i，j）=div_max；

（5）采用三角形线性插值获取子网格中心高程，然后根据质量守恒定律和动量守恒定律确定子网格水位、流量和污染物浓度［15］；

（6）判断并调整子网格（i，j，is，js）大小和其8个邻居网格大小之间满足2∶1准则［13］；

（7）如果gradΦ，is=1，…，Ms，js=1，…，Ms，Ms=2lev（i，j）均小于网格合并阈值Φcoar，则叶网格的划分层级设置为lev（i，j）=lev（i，j）-1，如果lev（i，j）=0，则保持lev（i，j）=0，合并得到的母网格中心状态变量为4个子网格中心状态变量的平均值，该过程同样保证网格（i，j，is，js）大小和其8个邻居网格大小满足2∶1准则。

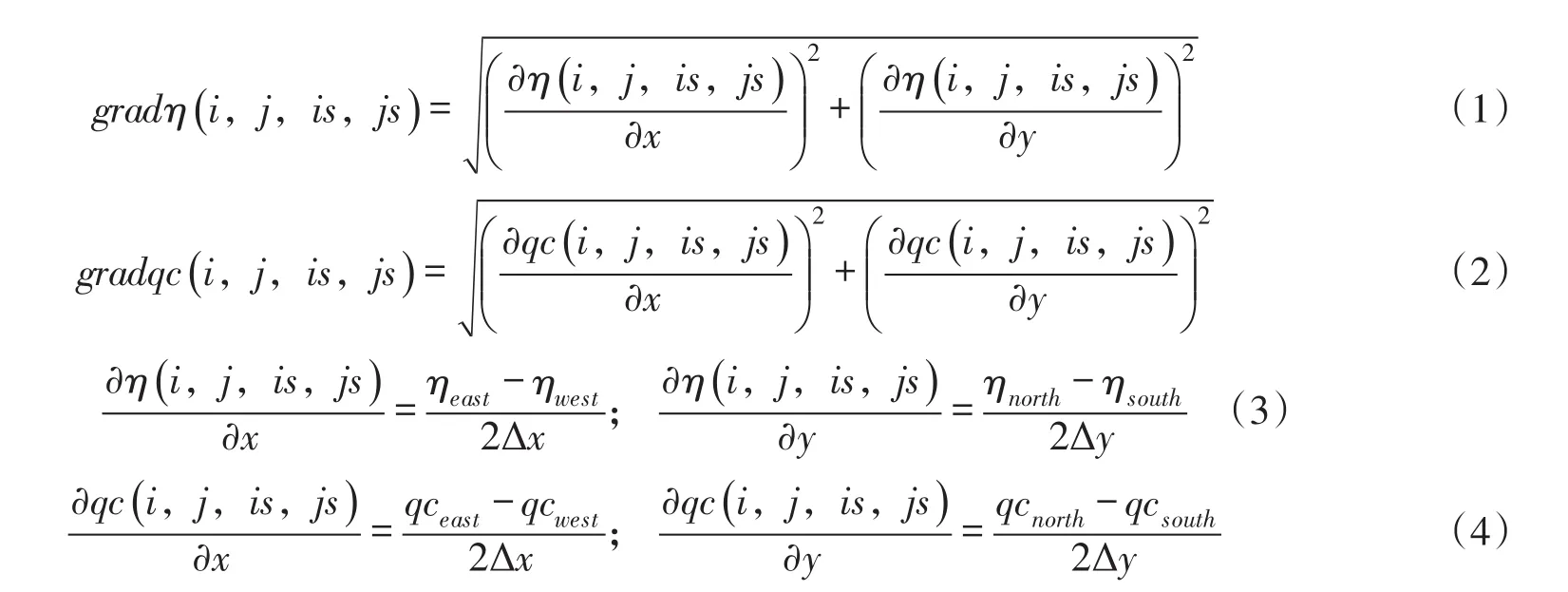
式中:ηeast、ηwest、ηnorth、ηsouth和qceast、qcwest、qcnorth、qcsouth分别为单元（i，j，is，js）东、西、北、南4个方向的水位和污染物守恒浓度，当网格（i，j，is，js）的划分层级和其邻居网格的划分层级相同时，则网格（i，j，is，js）邻居方向的水位和污染物守恒浓度直接取邻居网格中心的水位和污染物守恒浓度，否则通过自然邻近插值获取该方向的水位和污染物守恒浓度［16-17］。

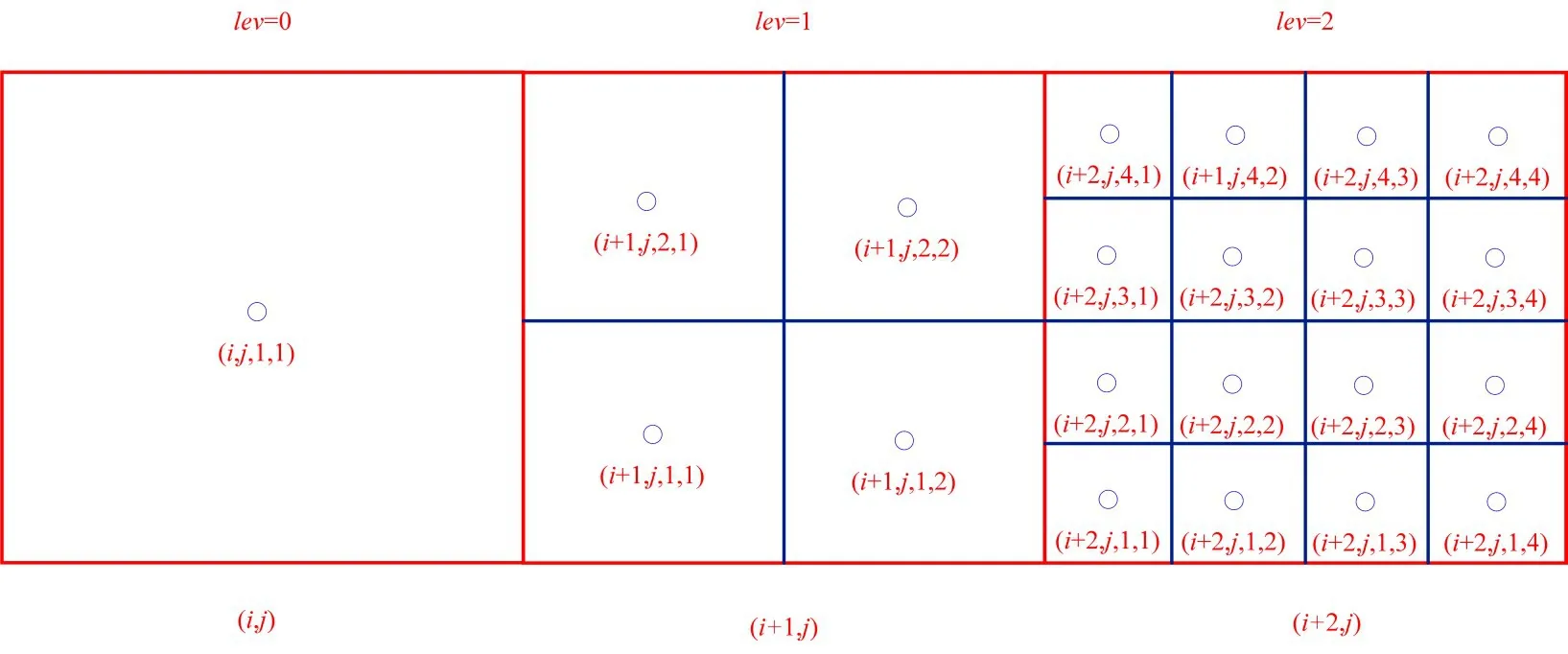
图1 自适应网格示意图

自适应网格生成技术常采用水位、水深、流速或者污染物质量、浓度梯度等设置网格划分阈值，阈值设置存在两种形式:相对阈值［5］和绝对阈值［13］。相对阈值通过对所有计算网格梯度grad进行降序排列，取某个分位数Sa处的梯度作为阈值，相对阈值在计算过程中会不断变化；相对阈值设置简单，但当多数网格均存在较大梯度时，基于相对阈值的自适应网格技术只能识别和细化部分（计算网格总数×Sa）大梯度网格，影响模型模拟精度；当水流趋于平稳，大部分网格梯度均较小时，基于相对阈值的自适应网格技术仍会对部分网格（计算网格总数×Sa）进行细化，影响计算效率。绝对阈值采用固定梯度作为阈值，对梯度大于该阈值的网格进行细化，直至达到最大划分层级；当多数网格均存在较大梯度时，基于绝对阈值的自适应网格技术能够更准确地识别并细化大梯度网格，当多数网格梯度均较小时，低于绝对阈值的子网格将会被识别和合并。相比于相对阈值，绝对阈值可以更好地识别和细化大梯度网格、合并小梯度网格，提高模型模拟精度和计算效率。

3 控制方程

在满足静水压力和忽略水体垂向加速条件下，利用水深平均的三维Navier-Stokes方程可以推导得到二维浅水方程［13，18］，加上描述物质输移的对流-扩散方程［19］，二维水流-输运方程形式如下:

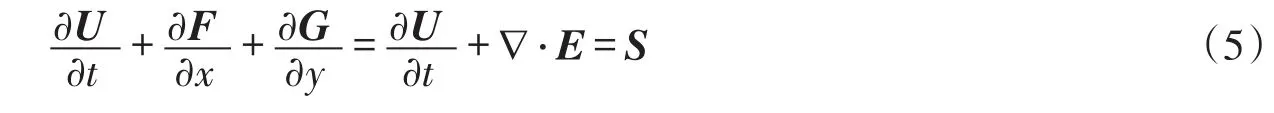
式中:t为时间，x和y分别为水平横向和纵向坐标；U为守恒变量；E为对流项通量，E=（F，G）；F、G分别代表x、y方向的对流通量；S为源项。

其中U、F、G和S表示如下:

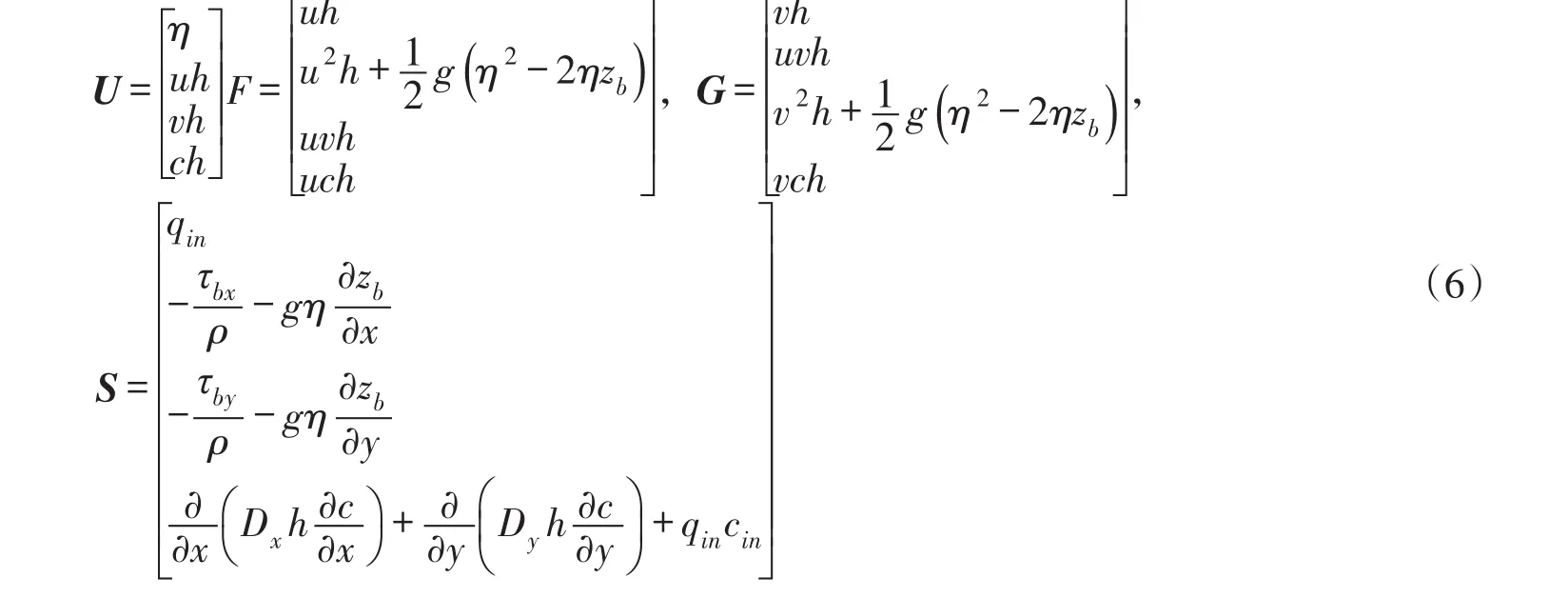
式中:η、h和zb分别为水位、水深和河底高程，η=zb+h；u和v分别为x和y方向流速；g为重力加速度；ρ为水密度；Dx和Dy表示x和y方向的扩散系数，c为物质的垂线平均浓度，qin和cin分别表示点源的流量强度和物质垂线平均浓度；τbx和τby为x和y方向的床面摩擦应力，表示因床面摩擦导致的水流能量耗散（式（7））。

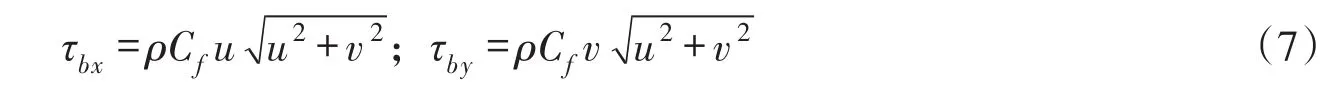
式中:Cf为床面摩擦系数，Cf=gn2/h1/3，n为Manning糙率系数，s/m1/3。在涉及干湿边界计算的案例中，设置一个最小水深，当单元水深小于最小水深时，Cf取0。

4 数值求解

采用有限体积法离散控制方程，在任意控制体Ω上对式（5）进行积分:

通过高斯-格林公式将∫Ω∇⋅E dΩ转化为沿控制体边界的面积分，得到式（9）:

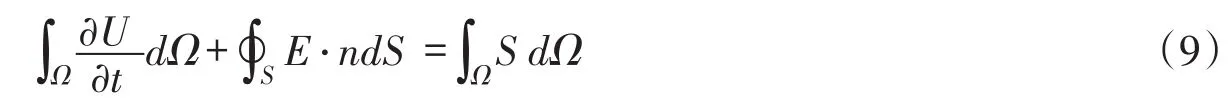
式中:U为单元均值；S为控制体Ω的边界；n为垂直于面元dS的单位向量。在笛卡尔坐标系下，式（9）中的曲面积分项可以转换为:

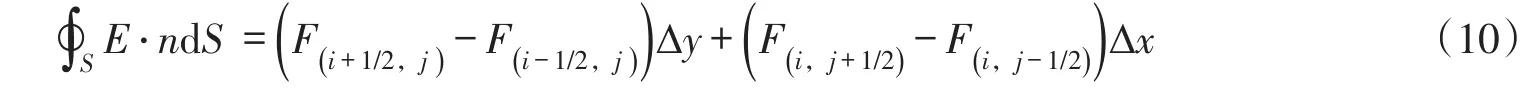
式中:Δx和Δy分别为笛卡尔坐标系中网格单元（i，j）的左右和上下边长，F（i+1/2，j）、F（i-1/2，j）、F（i，j+1/2）和F（i，j-1/2）分别为单元东、西、南和北4个界面的界面通量（图2）。

采用自适应网格时，网格单元和邻居网格单元可能处于不同的划分层级，当网格单元右侧的邻居网格划分层级大于该网格单元的划分层级时，此时通过东边界面的通量的计算需要w1、e1、w2和e2位置的状态变量，e1和e2位置状态变量可以直接获取，w1和w2位置状态变量可以通过自然邻近插值获取（图2）［16-17］。

由式（9）—式（10）可以得到由n时层到n+1时层推进的守恒有限体积公式:

为了使模型数值解具有时空二阶精度，采用MUSCL-Hancock方法求解控制方程，MUSCL-Hancock方法包括预测步和校正步两步。

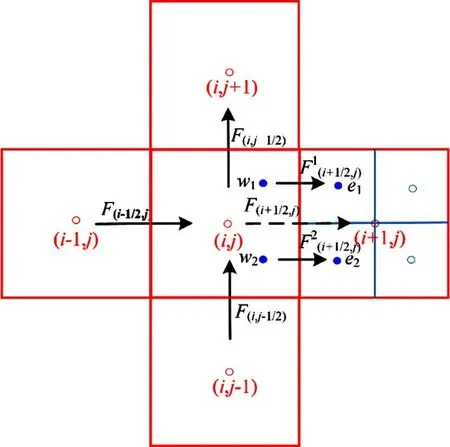
图2 自适应网格通量计算示意图

预测步中，利用n时层单元（i，j）和4个邻近单元中心状态变量U重构单元（i，j）4个界面左右的状态变量，以界面（i+1/2，j）为例，界面左侧状态变量UL（i+1/2，j）和右侧状态变量UR（i+1/2，j）重构如下:

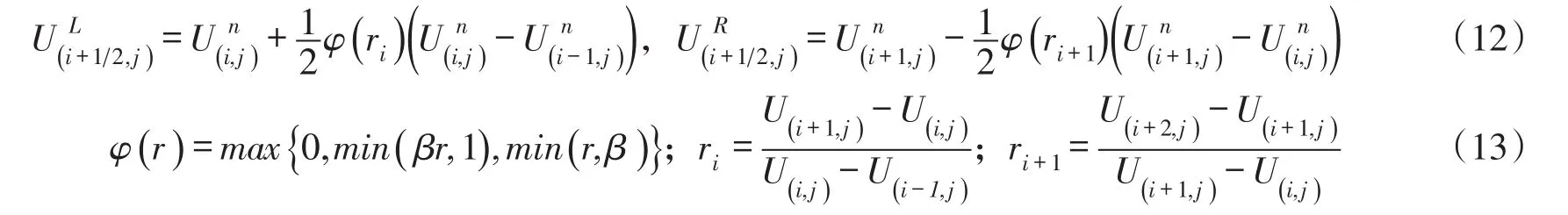
式中:φ()r为坡度限制器，限制器根据β（1≤β≤2）取值不同分为Roe’s minmod限制器（β=1）和Roe’s superbee限制器（β=2）。本文采用Roe’s minmod限制器。

基于重构后的界面左右状态变量，计算界面数值通量F*，然后代入式（14）计算n+1/2时层单元（i，j）中心状态变量值

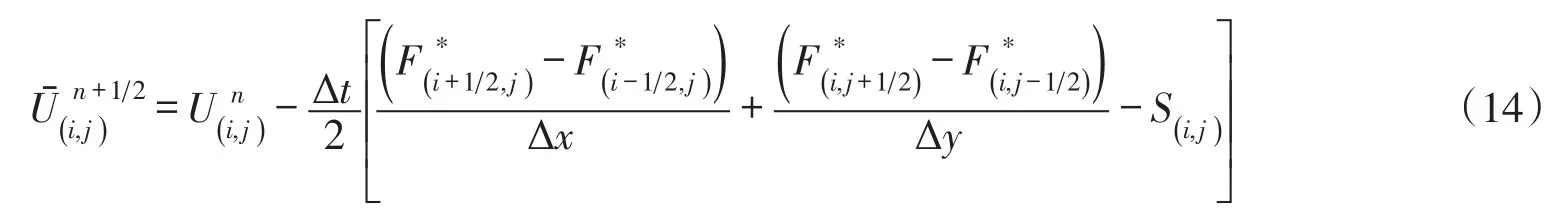
校正步中，基于预测步获取的n+1/2时层单元（i，j）和4个邻近单元中心状态变量12采用非负线性重构技术［11］和局部底部高程修正方法［13］对界面左右状态变量进行空间重构，利用HLLC近似黎曼求解器［20］计算界面通量F*n+12，然后代入式（15）计算n+1时层单元（i，j）中心状态变量值

5 结果与讨论

为了检验模型模拟急流条件下污染物输移的能力，分别利用水槽试验、物理模型和实际案例等经典算例检验模型模拟精度、稳定性以及模拟效率。3个算例中网格细化和粗化的绝对阈值分别设置为0.08（Φsub）和0.05（Φcoar）。所有算例中重力加速度g取9.81 m/s2，水体密度ρ取1000 kg/m3。

5.1 均匀浓度的水槽溃坝水流-输运模拟本算例［20］常用于检验模型的计算精度以及动态变化干湿边界处理的有效性。计算域为75 m×30 m，大坝位于x=16 m，忽略大坝厚度。糙率n=0.018 s/m1/3。底部高程计算公式为:

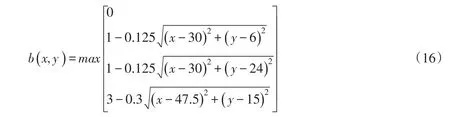
大坝上游初始水位和物质浓度分别取1.875 m和1 mg/L，流速设为0；下游水深为0，即干河床；模拟污染物输移过程中不考虑物质降解。x和y方向的扩散系数Dx和Dy均取0.5 m2/s。假设t=0 s时大坝瞬时全溃。由于初始条件为均匀浓度水体，因此，水体的物质浓度不随时间变化，始终为1 mg/L。

初始条件（t=0 s）及不同时刻（t=10、20、30 s）的流场、物质浓度计算结果如图3所示，不同时刻的网格分布和网格数如图4和图5所示。由图3可知，溃坝水流演进过程中水体的物质浓度始终保持为1 mg/L，模型模拟准确。由图4可以看出，网格划分层级随着溃坝水流演进不断的变化，由于地形和初始条件的对称性，水体流速和水质状态时刻保持对称，因此自适应生成的网格同样具有对称性；由图5可以看出t=14 s时网格最多，网格数为18 411，随后网格数逐渐降低，最后网格数稳定在11 226附近。自适应网格技术可以自动捕捉高水位梯度和高污染物浓度梯度所在区域以及干湿边界区域，对这些区域的网格进行细化，提升模型对这些区域水流和物质输移的捕捉能力。此外，自适应网格技术可以提高模型模拟效率，t=300 s时基于自适应网格的模型模拟时间为1055.8 s，如果采用自适应网格中最大划分层级的网格作为固定网格，模型模拟时间为2370.5 s，自适应网格技术可以节约55.5%的计算时间。

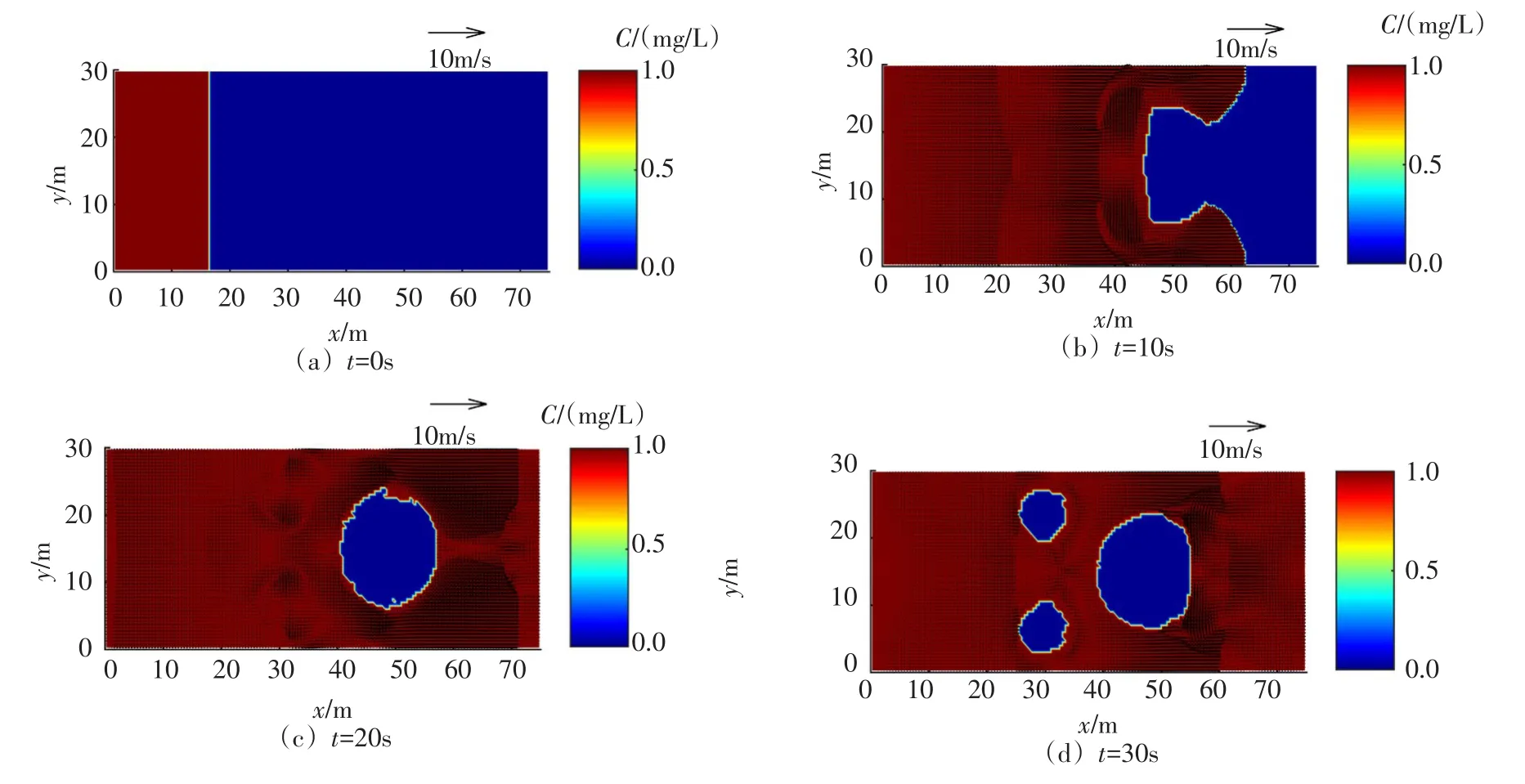
图3 不同时刻溃坝水流流场和污染物浓度模拟结果

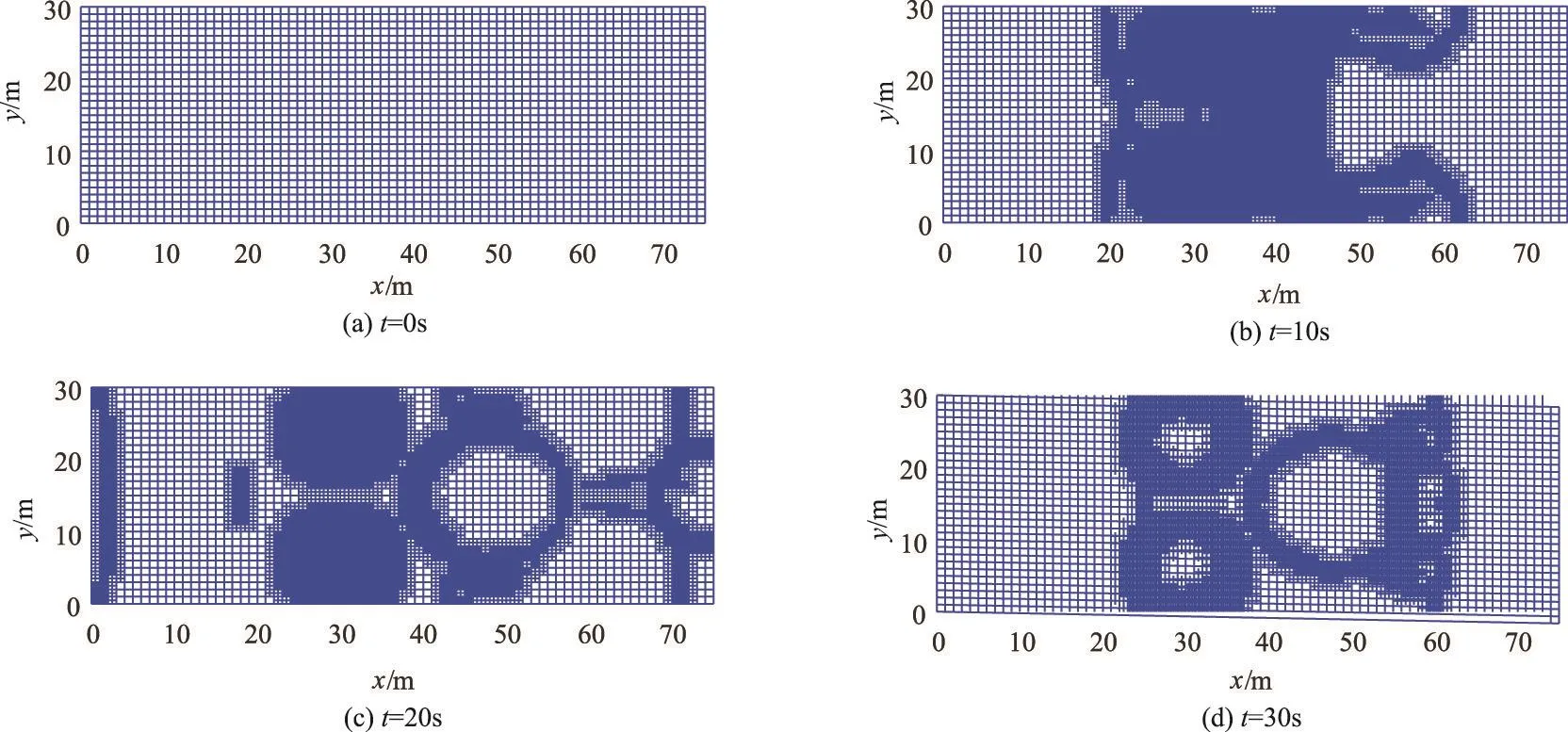
图4 不同时刻网格分布

5.2 Toce河溃坝物理模型案例Toce河模型［21］是意大利国家电力公司ENEL按1∶100的比例尺对意大利米兰市Toce河上游约5 km范围内建立的物理模型，该模型常用于验证各种溃坝数学模型的精度和稳定性。该物理模型长约50 m，宽约11 m。模型提供空间分辨率为5 cm的高程点，比较精确地描述了Toce河的真实地形。Toce河物理模型的地形、观测点位置以及出入流边界位置如图6所示，Toce河中部有一个空水库，水库在靠近河流一侧有个开口。Toce物理模型入流流量过程如图7所示。模型初始水深为0 m，出口为自由出流边界（图6）；糙率取ENEL推荐的0.0162 s/m1/3；模型模拟初始网格大小为0.4 m×0.4 m，最大细分水平设置为2。假设从溃坝发生后第25秒开始，位于［7.868，5.882］处的一个点源开始释放污染物，污染物释放速度为1 m/s，污染物浓度为1 kg/m3，污染物的扩散系数为0.01 m2/s。

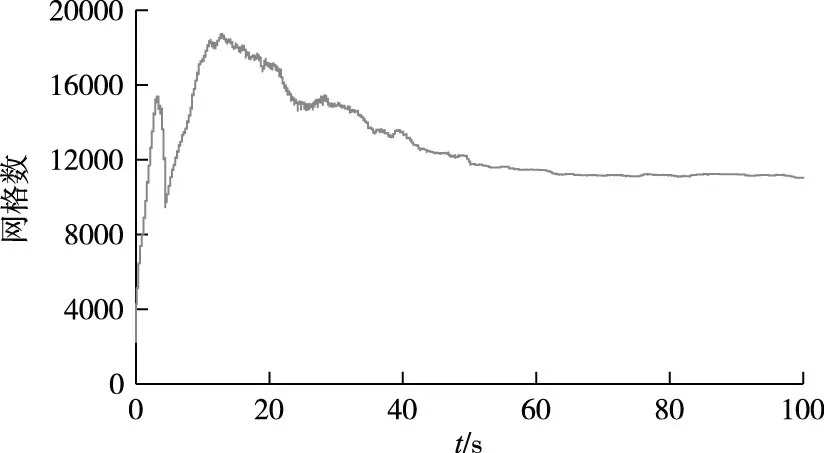
图5 自适应网格数随时间变化图

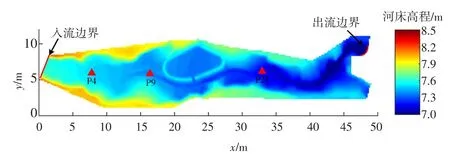
图6 Toce河物理模型地形

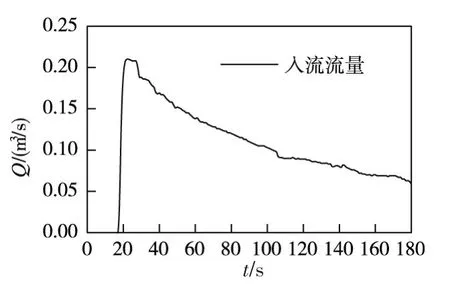
图7 入流流量过程

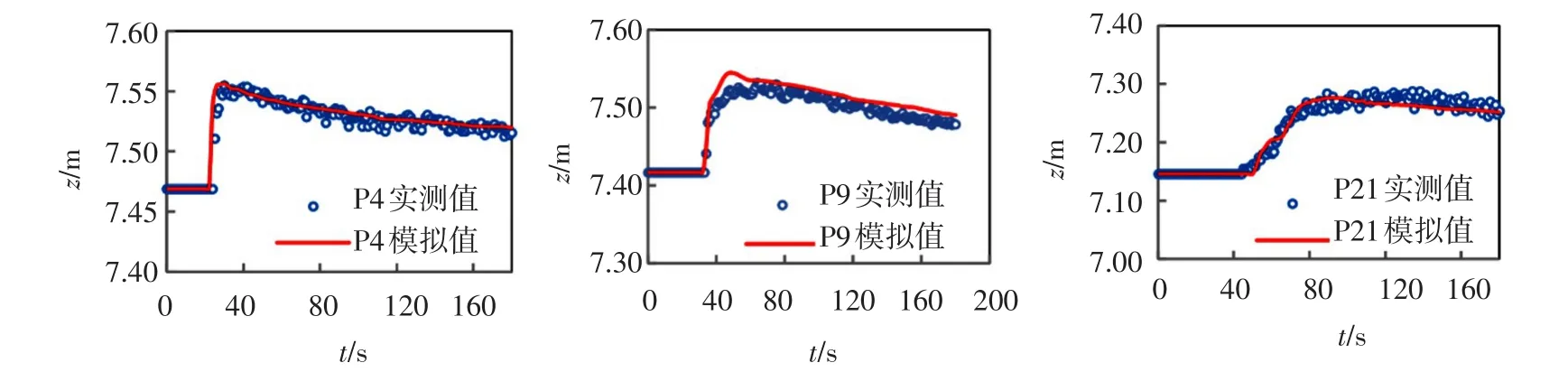
图8 水位实测值和模拟值

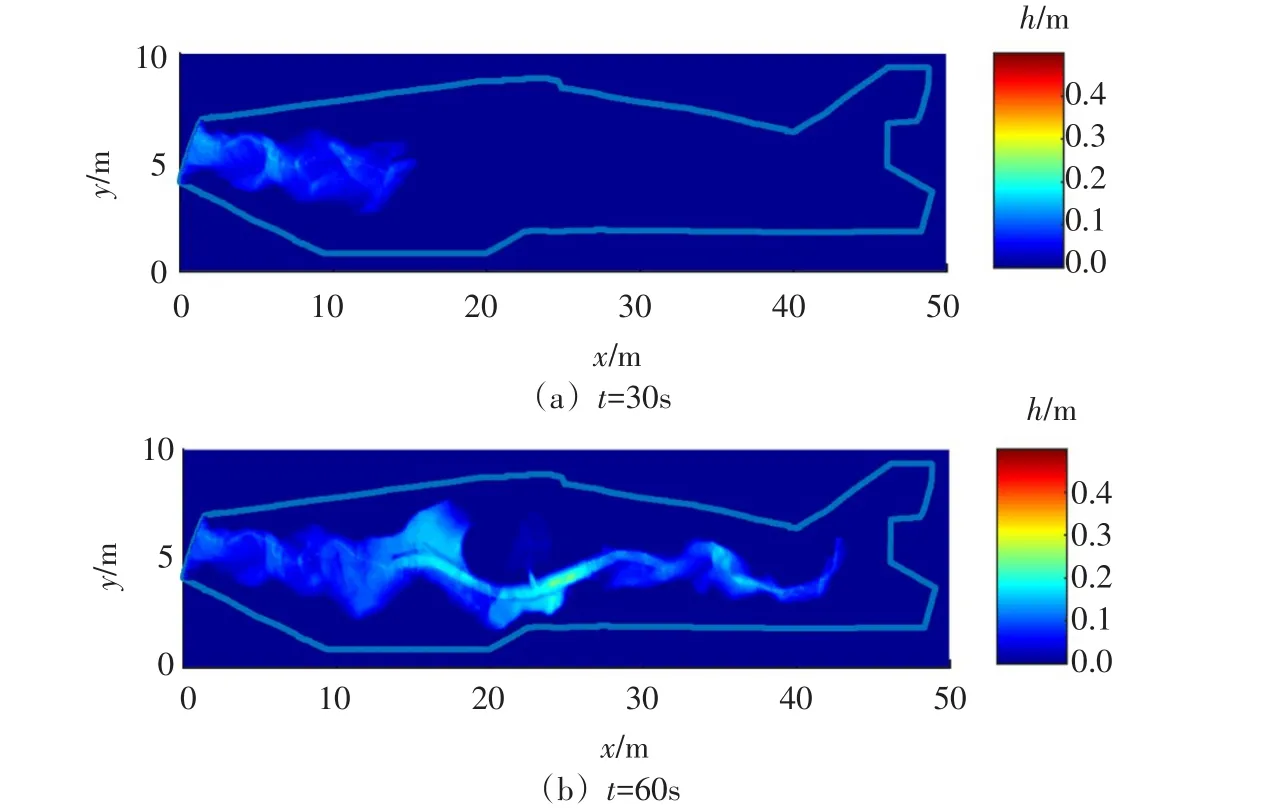
图9 t=30s和60s模拟水深分布

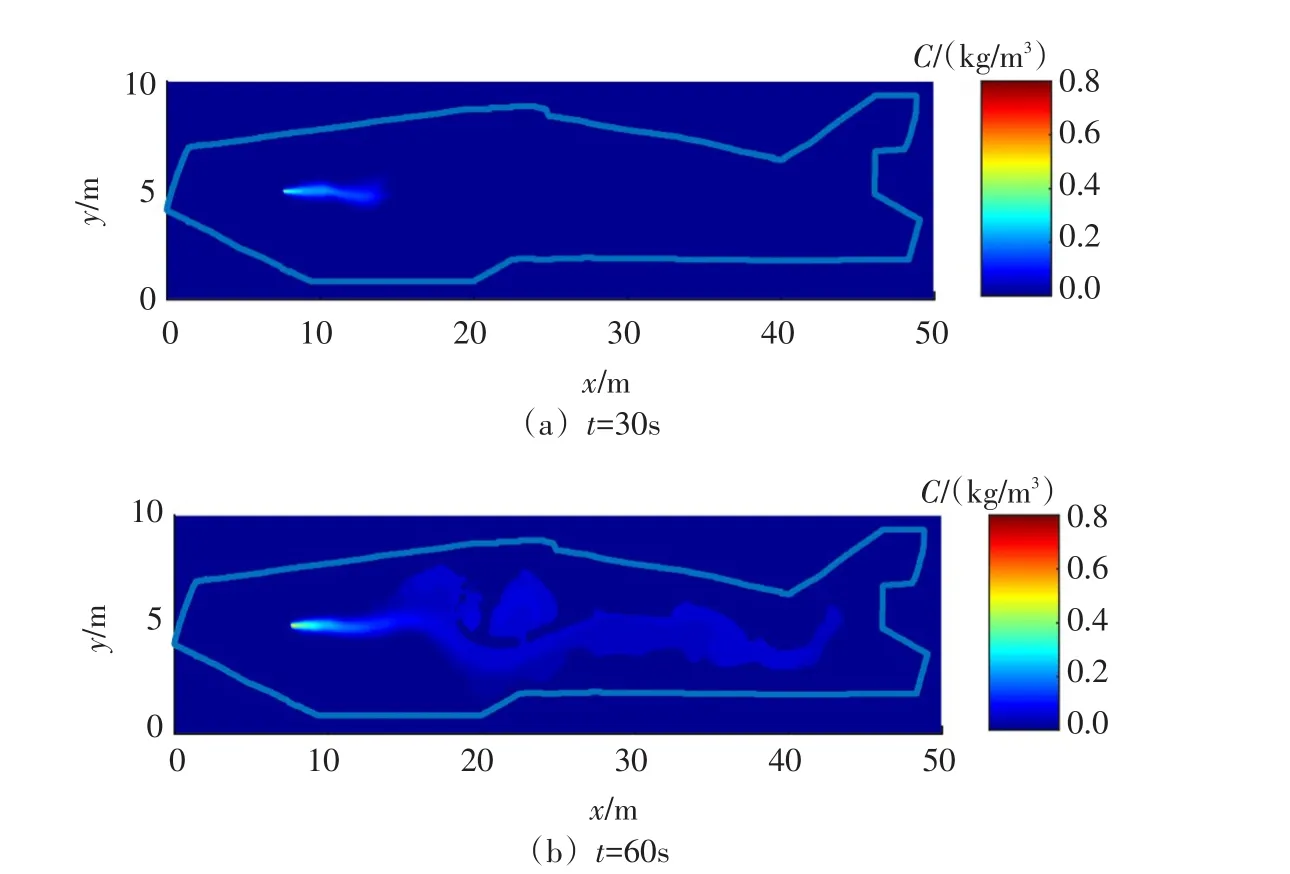
图10 t=30s和60s模拟水质分布

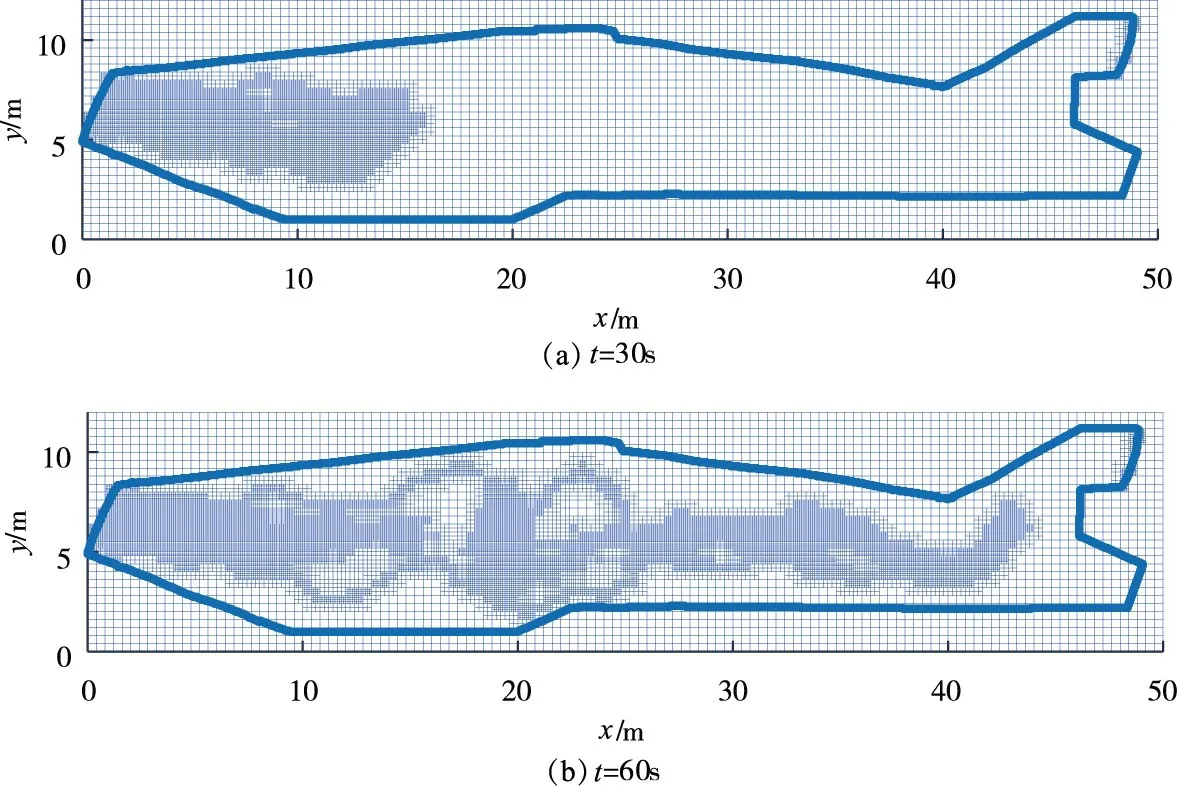
图11 t=30s和60s模型网格分布

图8为t=0～180 s模拟时间内P4、P9和P21点水位模拟值和观测值对比图，3个观测点处模拟水位和观测水位基本一致，模型具有很高的模拟精度。图9为t=30 s和60 s的模拟水深分布，可以看出随着t=18 s溃坝开始（图7），溃坝洪水流速很快，快速向下游演进。图10为t=30 s和60 s模拟污染物浓度分布，可以看出，急流条件下如果突发水

污染事故，污染物会随着水流迅速向下游扩散。图11和图12为t=30 s和60 s的网格分布以及模拟过程中网格数的变化情况，溃坝开始前，计算网格为2461，t=18 s溃坝开始后，溃坝水流向下游快速演进，洪水经过区域具有较高的水位梯度，加上点源污染物释放后的运移产生的污染物浓度梯度，导致网格数快速增加，t=78 s时达到最大值16 930个，随后逐渐降低，稳定在15 300附近。t=180 s时基于自适应网格的模型模拟时间为365.3 s，相较于基于固定网格的模型模拟时间（435.2 s），节省了16.1%的模拟时间。由于溃坝水流经过的大部分区域均具有较高的水位或污染物浓度梯度，因此，需要相对较细的网格捕捉水流和污染物输运特性，自适应网格可以自动捕捉具有高水位梯度和高污染物浓度梯度以及干湿边界区域，细化该区域网格，保证该区域模型模拟精度。

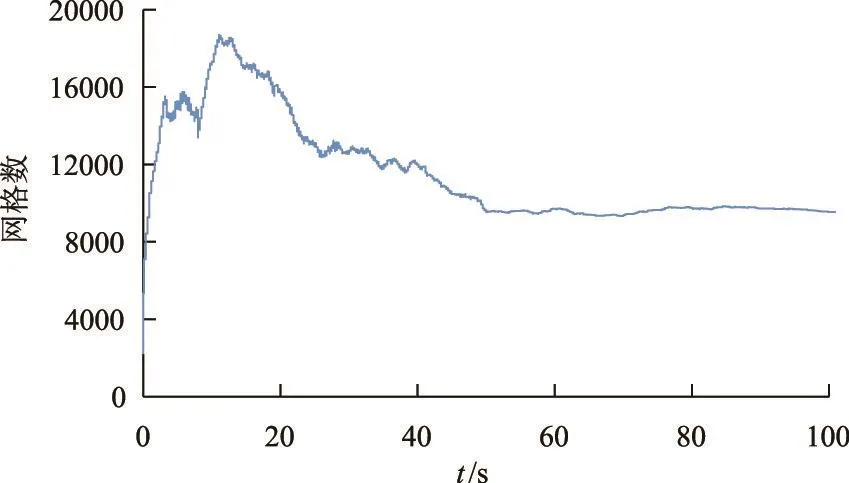
图12 t=0～180s自适应网格数随模拟时间变化图

5.3 Malpasset溃坝实际案例法国Malpasset大坝建于1956年，最大库容为5500万m3，主要用于农业灌溉和城市用水。由于1959年11月底连降暴雨，Malpasset大坝水位短时间内迅速上升，大坝最终于12月2日21时14分溃决，溃坝历时很短，可认为是瞬时溃坝，Malpasset水库及下游地形如图13所示。溃坝水流迅速向下游演进，最终进入大海，海面高程为0 m；溃坝前，大坝上游水位为100 m，下游水深为0 m。假设溃坝900 s后位于（9660 m，3074 m）的位置突发污染物排放，排放的污染物浓度为1 kg/m3，排放强度为1 m/s，污染物扩散系数为0.5 m2/s。利用基于自适应网格的二维水流-输运耦合模型模拟溃坝水流演进和污染物迁移扩散，初始网格大小为80 m×80 m，最大细分水位设为2，Manning糙率系数取0.033 s/m1/3。

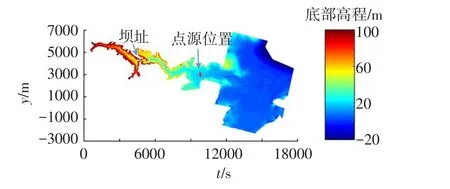
图13 Malpasset水库及下游地形

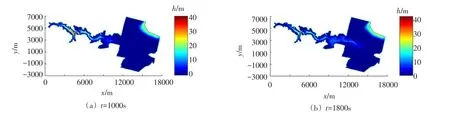
图14 Malpasset溃坝洪水演进过程

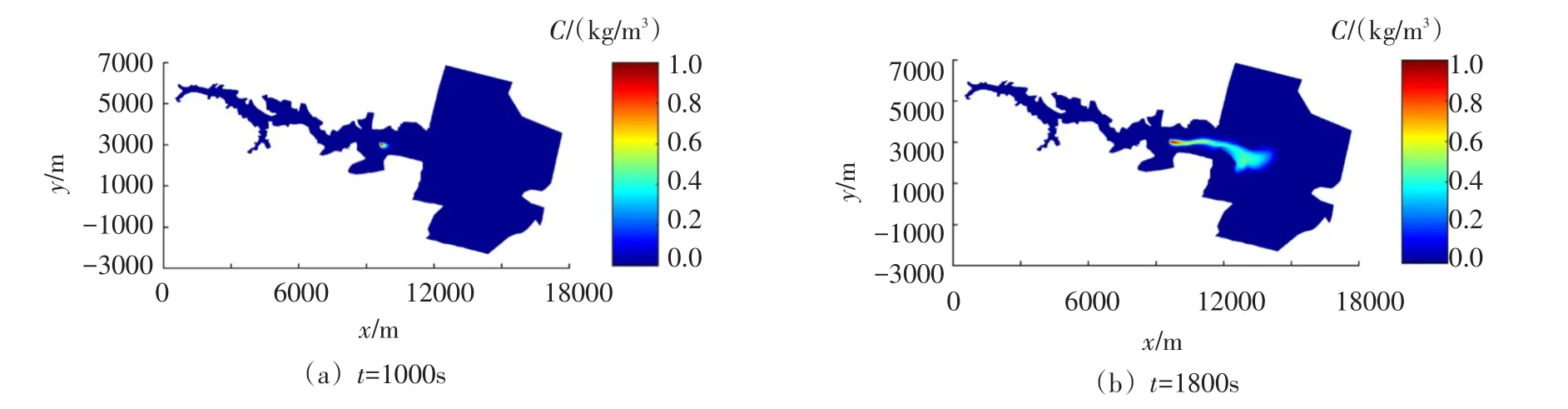
图15 Malpasset溃坝水流污染物运移和扩散过程

图16 不同时刻网格分布

模型模拟溃坝后1000 s和1800 s的水深和污染物浓度分布分别如图14和图15所示。溃坝后洪水向下游快速演进，t=1800 s时水流已经到达下游平原，和Hou等［22］模拟结果一致。t=900 s时水流已经经过（9660 m，3074 m），随着污染物的释放，污染物随水流往下游迁移，同时由于浓度梯度的存在污染物逐渐向周围扩散，污染物浓度沿着水流演进方向逐渐降低。图16为1000 s和1800 s模型网格分布，自适应网格技术可以识别水位和污染物浓度梯度，自适应调整网格大小，同时可以捕捉干湿边界变化，在干湿边界处对网格进行细化，提高水位梯度和污染物浓度梯度较大区域以及干湿边界处数值模拟精度。t=3000 s时基于自适应网格的模型模拟时间为860.4 s，相较于基于固定网格的模型模拟时间（1515.1 s），节省了43.2%的模拟时间。

6 结论

本文基于自适应网格技术构建了一种适用于复杂地形和急流条件下突发水污染事件中污染物输运模拟的二维水流-输运耦合模型，分别利用水槽试验、物理模型以及实际算例验证了模型精度和稳定性。验证结果表明:（1）基于自适应网格技术的二维水流-输运耦合模型可以捕捉高水位梯度、高物质浓度梯度和干湿边界区域，并对这些区域网格进行细化，模拟精度高；（2）自适应网格技术在保证模型模拟精度的同时，可以提升模拟效率；（3）基于自适应网格技术的二维水流-输运耦合模型能够准确高效地模拟急流条件下污染物的输运过程，适用于突发水污染事件的评估、预警和应急管理，具有推广应用价值。未来将在模型中考虑COD、BOD、TN和TP等水质指标，研究突发水污染事件中多种目标污染物的输运规律。