考虑河流流速和横向扩散系数变化的污染混合区理论分析及其分类

武周虎

（青岛理工大学 环境与市政工程学院，山东 青岛 266033）

1 研究背景

市政、工业和其它来源的污/废水经处理后，通过岸边排放口泄入河流。在河流中经初始稀释阶段之后，污染物在垂向上可以达到均匀混合，再进入污染带扩展阶段。因此除近区以外，可以作为二维移流扩散问题处理［1-3］。通常应用物理模型或数学模型来研究污染带的横向扩展以及对于环境的影响，而横向扩散系数（又称横向混合系数）是模型的重要参数和解决问题的关键之一［4-5］。在环境水力学中，常常是按照污染物浓度横向分布服从正态分布规律，结合室内或现场试验资料采用浓度矩法、直线图解法、线性回归法和模型演算法等方法［6-10］，或者采用基于剪切流分散理论的横向速度与深度平均值的偏差流速［11-13］，来确定矩形断面明渠和天然河流横向扩散系数，其分析结果是将横向扩散系数处理成常数，即横向扩散系数在整个断面上采用常数。长期的研究大多致力于寻求横向扩散系数与河段（或断面）平均水力学参数之间的半理论半经验关系式［14-20］。在实践中，通常采用常数横向扩散系数来进行河流水环境影响预测和计算河流排污混合区［21-24］。

赵振祥等［25］通过采用断面平均方法，对具有相同横断面面积、水面宽度、平均水深和平均流速的矩形与梯形断面的扩散浓度分布比较发现，梯形断面岸边斜坡上的浓度明显高于矩形断面岸边区域的浓度。Fischer H B等人［1］根据独立实验给出横向扩散系数Ey∝h（其中h是平均水深），即水深浅的地方横向扩散系数小，据此赵振祥等［25］提出横向扩散系数在整个断面上是变化的概念。并对莱茵河某河段的横向扩散系数进行了计算，得出全断面上无量纲横向扩散系数为αy=0.20，岸边污染带（y=60 m）内的无量纲横向扩散系数为αy1=0.14，相对误差为30%。在大江大河中岸边排放的污染带通常位于具有斜坡的岸边，斜坡上的横向扩散系数与整个断面上的平均横向扩散系数是不一样的。因此，采用整个断面上的平均物理量去反映河流岸边的局部地形特征，取横向扩散系数为常数是不妥的。

由于在以往的河流横向扩散系数确定中，常常是根据污染物浓度的横向分布监测结果进行，忽视了对于河流移流扩散污染物二维浓度分布特征的监测分析，导致河流横向扩散系数在整个断面上的变化特征未得到应有的重视。直到武周虎等［26］和Wu等［27］基于河流平均流速和常数横向扩散系数，在顺直河流岸边稳定点源条件下推导出二维移流扩散污染混合区边界归一化（等浓度）曲线方程才发现，据此得到的污染混合区形状特征，如最大宽度对应的纵向坐标与最大长度之比等于1/e（数学常数e=2.7183），不能解释黄真理等［28］在长江三峡建水库前库区水环境现状及水文水质污染负荷同步观测中得到的黄沙溪排污混合区形状。事实上，污染混合区边界曲线能很好地反映污染物的二维浓度分布特征，河流横向扩散系数在整个断面上的变化，会直接影响污染混合区边界曲线的形状特征［29-31］。

Wu等［29-30］分析了河流大涡紊动对“污染云”扩散的主导作用，参照有风时大气扩散参数的指数形式，假定河流变横向扩散系数Ey(x)=γxα，式中:γ，α为正常数。在顺直河流岸边稳定点源条件下，求解了二维移流扩散方程浓度分布的解析解，推导出污染混合区边界曲线方程，给出最大宽度对应的纵向坐标与最大长度之比等于exp［-1（/1+α）］。虽然现场观测的污染混合区最大宽度对应的纵向坐标位置，可以通过拟合变横向扩散系数中的正常数指数α得到满足，但是污染混合区形状曲线的吻合程度还是相差较大［28］；Wu等［31］又分析了河流从岸边到中间的流速和横向扩散系数的变化特征，参照下层大气水平流速和垂向扩散系数随高度按指数律变化的经验公式，假定河流深度平均流速和横向扩散系数的横向分布服从u=u1(y/y1)m，Ey=Ey1(y/y1)n，式中:u1和Ey1分别代表离岸横向坐标y（1≤W/2）点的流速和横向扩散系数值，W为河流宽度。在顺直河流岸边稳定点源条件下，求解了二维移流扩散方程浓度分布的解析解，推导出污染混合区边界曲线方程。污染混合区最大宽度对应的纵向坐标相对位置与常数横向扩散系数时相同，现场观测的污染混合区形状曲线的吻合程度，可以通过拟合流速和横向扩散系数横向分布的正常数指数m和n得到满足。由此可以看出，单独考虑横向扩散系数随纵向坐标x的变化，只能反映现场观测的污染混合区形状在纵向坐标方向的变化特征；而单独考虑流速和横向扩散系数的横向分布，也只能反映现场观测的污染混合区形状在横向坐标y方向的变化特征。因此，只有同时考虑以上两种情况，才能全面反映现场观测污染混合区形状的二维变化特征。

针对上述问题，本文通过对长江黄沙溪排污混合区平水期同步观测资料的分析，提出深度平均流速的横向指数分布和横向扩散系数的二维变化关系式。在宽阔河流顺直岸边稳定点源条件下，求解变系数二维移流扩散方程浓度分布的解析解，推导污染混合区最大长度、最大宽度和对应纵向坐标以及面积的理论公式，给出污染混合区边界归一化（等浓度）曲线方程。在结果分析基础上，提出污染混合区的类别、分类条件和变横向扩散系数的估算方法，可作为河流污染混合区范围的计算依据，也可以对水质建模起到理论指导作用。

2 浓度分布求解与特性分析

2.1 流速和横向扩散系数的关系式

（1）流速的横向分布在分析了黄真理等［28］给出的长江三峡建水库前库区水环境现状及水文水质污染负荷同步观测中，黄沙溪排污混合段平水期6个断面的深度平均流速横向分布观测值（如图1数据点所示）的基础上，对深度平均流速的横向分布选择指数分布规律［31］进行曲线拟合。

式中:u和u1分别为距离排放岸横向坐标y点和y1（≤W/2）点的深度平均流速；W为河流宽度；m是正常数指数。

对于按顺直河流进行简化处理的黄沙溪排污混合段，将全部6个断面的深度平均流速横向分布观测值一并采用指数分布式（1）进行回归分析得到:y1=150 m，u1=1.4 m/s，m=0.25，相关系数R2=0.7483，其相关性较好，在图1中以实线显示。

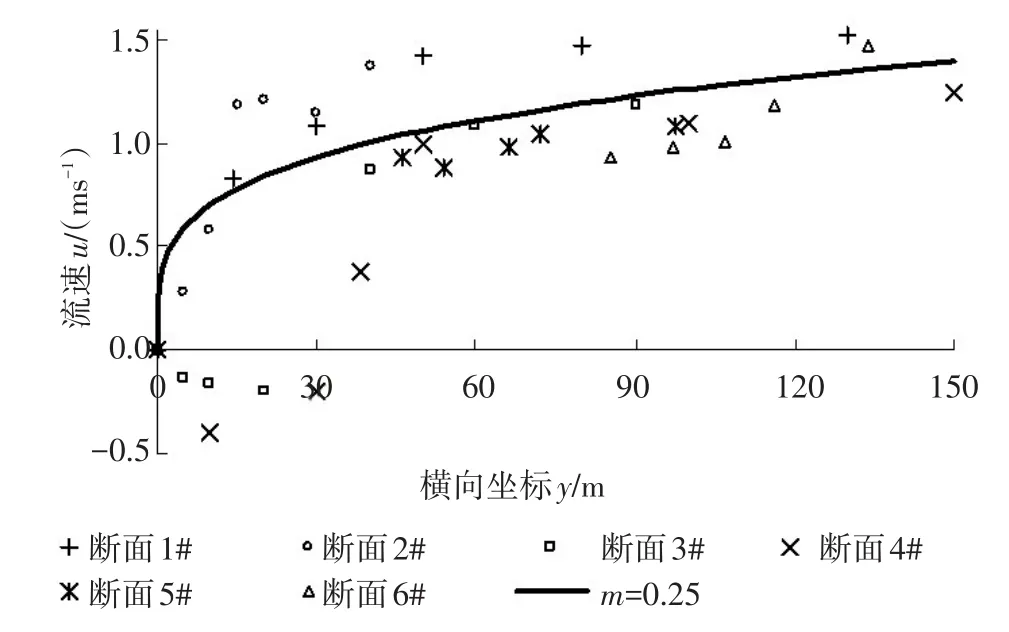
图1 黄沙溪排污混合段平水期深度平均流速的横向分布

（2）横向扩散系数的关系式根据Wu等［29-30］对河流二维移流扩散问题的分析，从岸边排污口排出的污染物扩散时间越长，迁移距离越远，扩散范围不断增大，大尺度涡旋体的扩散作用逐渐增强。考虑到大涡对“污染云”扩散的主导作用，因此有横向扩散系数随着污染云的扩散范围增大而增大，即河流横向扩散系数与迁移距离x成比例。另一方面，由于河岸地形对水流的摩擦阻力作用，河流近岸区域的流速一般低于中间区域，离岸距离越大，流速越大，横向扩散系数也越大。Wu等［31］根据河流深度平均流速的横向指数分布规律，提出横向扩散系数的横向分布同样服从指数分布规律。综合以上两种点，假设横向扩散系数既服从横向指数分布规律，又随纵向坐标x呈指数变化的关系式为:

式中:Ey为从排放口沿水流纵向坐标x、距离排放岸横向坐标y点的横向扩散系数；γ、α、n均为正常数。

2.2 岸边排放源在非均匀流场中的扩散根据张书农［4］、Wu等［31］和Li［32］在稳态条件下，对河流二维移流扩散方程的简化处理，在离开排放口一定距离后的远区，即xu≫Ex，纵向坐标x方向的扩散项与移流项相比，在纵向上的扩散作用微不足道，可以忽略不计；按照一般环境水力学概念，河流中的横向流速可以略去，在横向上的污染物主要表现为扩散与混合。因此，河流中的简化二维移流扩散方程为:

式中:x为自排污口沿河流流向的纵向坐标；y为垂直于x轴从排污口指向河心的横向坐标；u为深度平均流速；Ex和Ey分别是纵向和横向扩散系数；C为污染物浓度。

将式（1）和式（2）代入式（3），整理得到变系数二维移流扩散方程为:

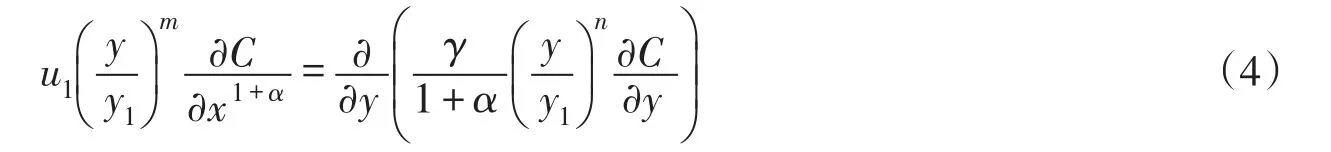
令X=x1+α，E=γ/( )1+α，式（4）变为:

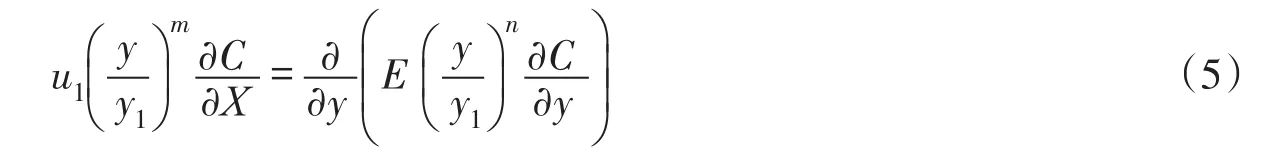
根据Wu等［31］在顺直矩形河渠中，在岸边稳定线源单位时间单位水深的排放质量m˙=M˙/H的条件下，对于保守物质，由式（5）给出深度平均流速和横向扩散系数均服从指数分布规律决定的河流二维移流扩散污染物浓度分布为:

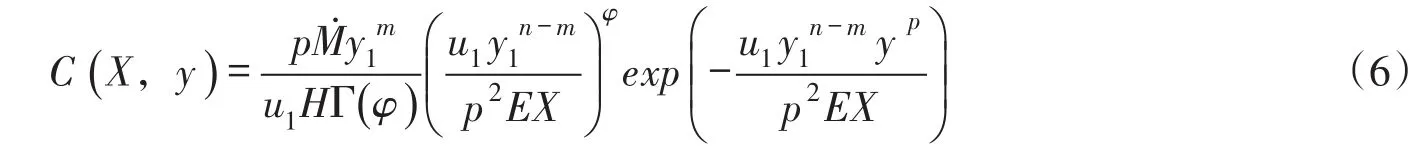
式中:p=2+m-n＞1；φ=（1+m）/p；Г（φ）为完全伽玛函数；M˙为岸边稳定点源单位时间的排放质量；H为平均水深。

将X和E代入式（6）整理得到，由深度平均流速的横向指数分布式（1）和横向扩散系数的二维变化关系式（2）确定的河流二维移流扩散污染物浓度分布为:

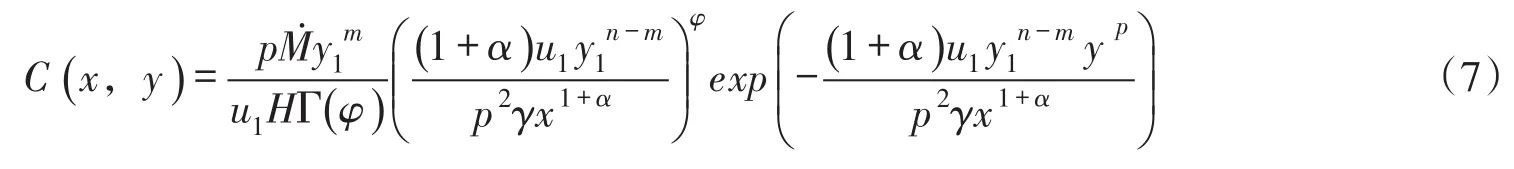
2.3 浓度分布特性分析由式（7）可以得到，对于纵向坐标的给定值（xi，i=1，2，3，…），河流岸边排放二维移流扩散污染物浓度的横向分布特征主要取决于exp（-yp）。即污染物浓度随横向坐标y的增大单调下降，横向浓度分布曲线类似于半正态分布形式；当纵向坐标x增大时，横截面上的最大浓度沿程逐渐减小，污染物浓度迅速在横向上扩展，浓度梯度迅速减小，如图2所示。

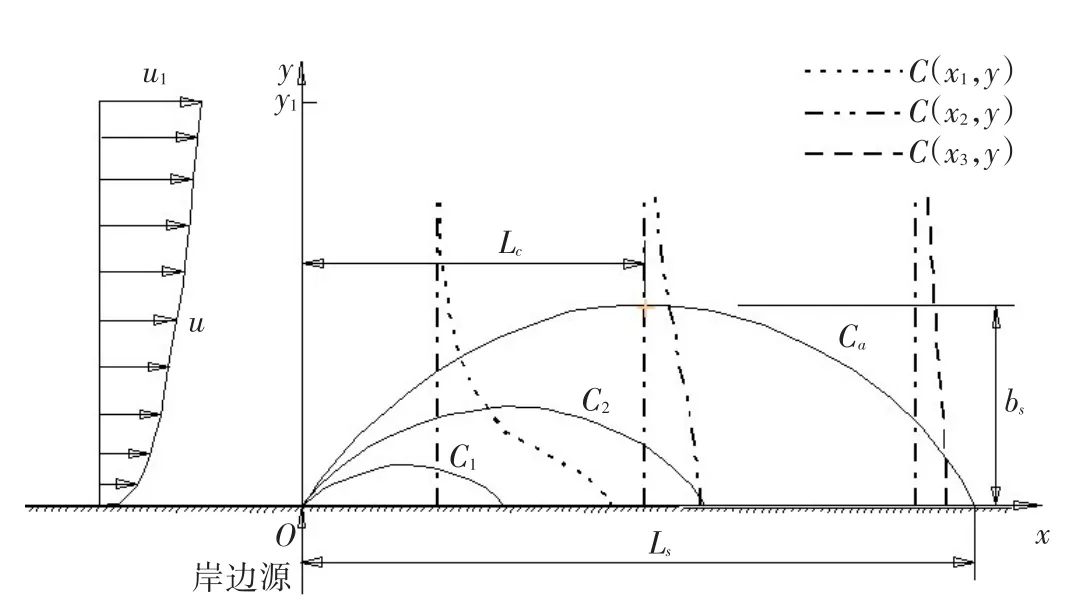
图2 河流岸边排放污染物浓度分布和等浓度线

令y=0，由式（7）可以得到横截面上污染物最大浓度的沿程分布为:

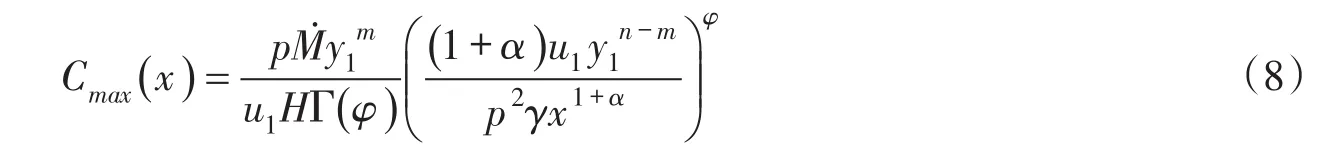
即横截面上的最大浓度随纵向坐标x的［-φ（1+α）］次方下降。

由于深度平均流速的横向分布不是常数，因此，河流中污染物浓度的横向分布不能代表污染物通量q（xi，y）=uC的横向分布。对于保守物质，在纵向坐标取任意值（xi）时，则有河流各断面的污染物总通量相等，即有:

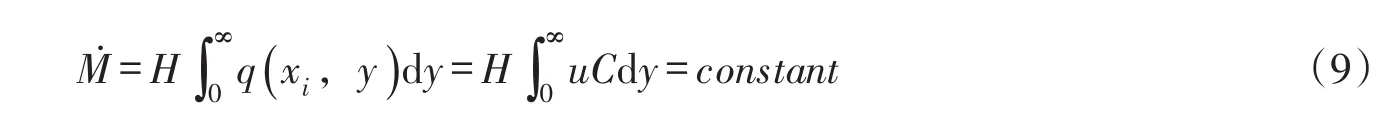
当α=0时，横向扩散系数与纵向坐标x无关，横向扩散系数和深度平均流速的横向分布均服从指数规律，式（7）变为与相同条件下Wu等［31］给出的结果一致；当m=n=0时，横向扩散系数和深度平均流速均在横向上保持常数，横向扩散系数仅随纵向坐标x呈现指数变化规律，式（7）变为与相同条件下Wu等［29-30］给出的结果一致；当α=m=n=0时，横向扩散系数和深度平均流速均取常数，式（7）变为与相同条件下Wu等［26-27］给出的结果一致。

3 污染混合区几何特征

根据污染混合区的概念，河流背景污染物浓度Cb与排放产生的允许升高浓度Ca的总和应符合水环境功能区所执行的浓度标准值Cstd，即有Ca=Cstd-Cb，该等浓度线所包围的区域称为污染混合区。

由式（7）可知，河流岸边排放的污染混合区边界（等浓度）曲线方程为:

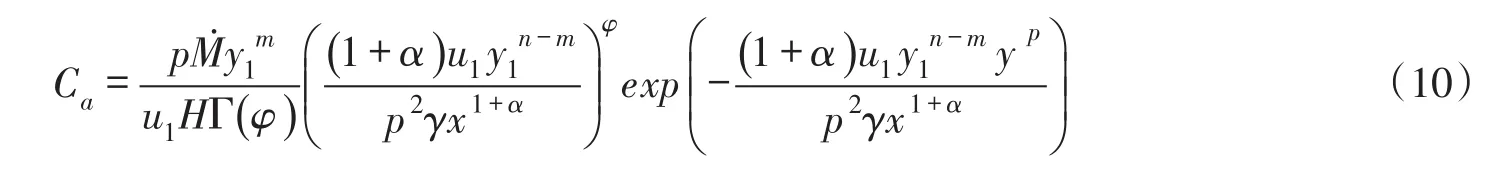
在图2中，绘制了3个水平C1＞C2＞Ca的浓度等值线。在以下小节中，将由方程式（10）具体分析污染混合区边界（等浓度）曲线几何特征参数的理论公式。

3.1 最大长度在式（10）中，令y=0，可以得到河流岸边排放污染混合区最大长度Ls的理论公式:

3.2 最大宽度和对应纵向坐标为了方便推导河流岸边排放污染混合区最大宽度和最大宽度对应的纵向坐标位置，改写式（10）为:

为了获得等浓度线上横向坐标y达到极大值点的坐标关系，给式（12）两边分别对x求导，并令dy/dx=0，整理得到:

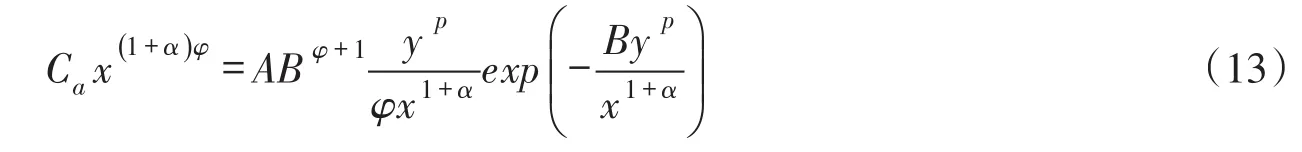
注意到，式（12）与式（13）的左边相同，则右边应该相等。据此，可以得到污染混合区最大宽度极值点的纵向坐标Lc和横向坐标bs应满足的关系式为:

将式（14）代入式（12），整理得到污染混合区最大宽度的理论公式为:

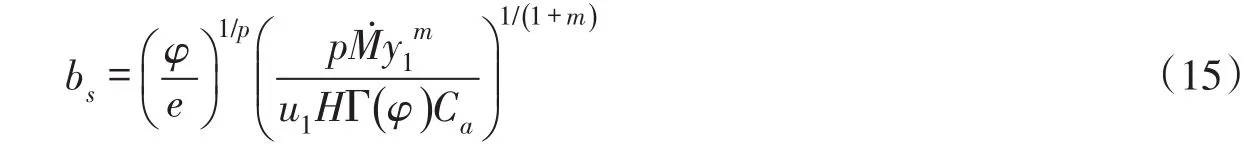
考虑到式（11），可以得到污染混合区最大宽度与最大长度的关系式为:

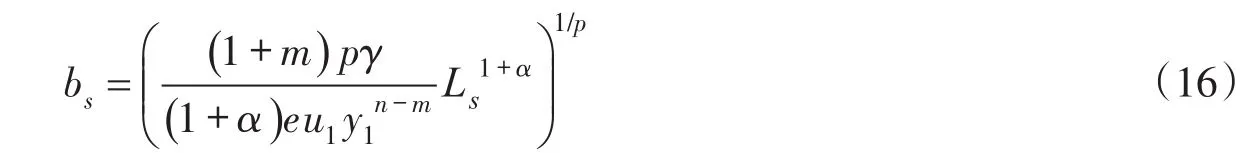
将式（16）代入式（14）化简得到污染混合区最大宽度对应纵向坐标与最大长度的关系式为:

其中:q=1+α＞1。

3.3 边界（等浓度）曲线方程在式（10）中，对坐标变量x除以Ls可以得到归一化坐标（x/Ls），同时乘以式（11）右边的最大长度表达式；对坐标变量y除以bs可以得到归一化坐标（y/bs），同时乘以式（15）右边的最大半宽度表达式，整理得到通用形式的河流岸边排放污染混合区边界曲线方程为:

或

值得注意的是，河流岸边排放污染混合区归一化坐标边界的曲线方程仅是p（=2+m-n）和q的函数。其它参数（m，n，γ，α，y1，u1，H，Ca和˙）仅改变用于归一化的两个几何特征参数Ls和bs。

3.4 面积和面积系数在纵向坐标x∈［0，Ls］上，对式（19）求定积分，可以推导河流岸边排放的污染混合区面积S如下:

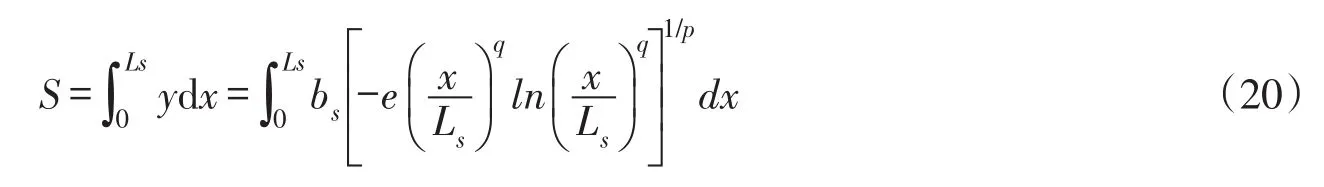
进行变量替换，令x/Ls=ζ，积分区间变为［0，1］，式（20）变为:

其中面积系数函数μ为:

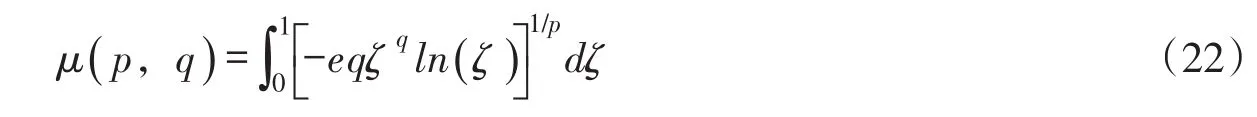
（1）在特定条件下，面积系数的理论公式

当p=1时，式（22）改写为:

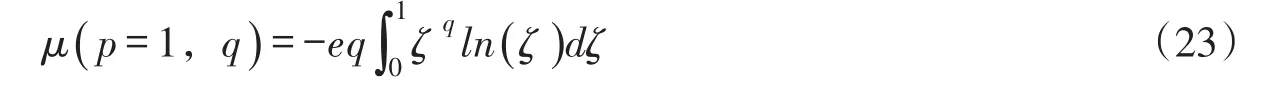
当p=2时，令η=ζ(2+q)/2，代入式（22）化简得到:

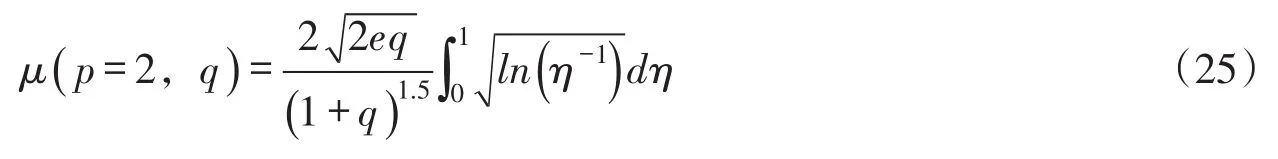
（2）在其它条件下，面积系数的数值积分公式

除p=1和p=2以外，式（22）不存在直接积分公式。可以借助于梯形法求定积分的公式，由式（22）得到污染混合区面积系数的数值积分公式为:

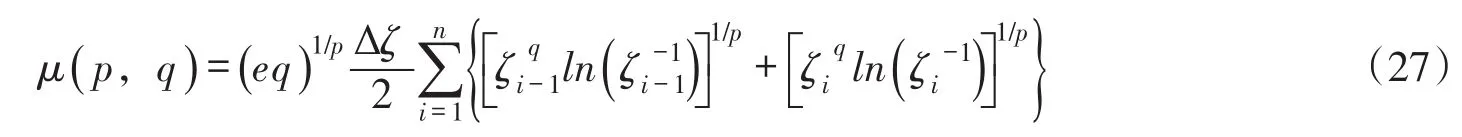
在式（27）中，将自变量ζ的积分区间［0，1］划分为n（=1/Δζ）等分，每一等分的长度Δζ取1×10-4，一般就可以实现数值积分值与理论值的误差绝对值小于1×10-4。若需进一步提高数值积分的精度，可以通过缩小等分长度或更换数值积分方法。

在河流流速和横向扩散系数均为常数（p=2，q=1）、仅横向扩散系数随纵向坐标x呈指数变化（p=2，q=1+α）以及流速和横向扩散系数为指数分布（p=2+m-n，q=1）条件下，式（24）或式（26）或式（27）可简化为与相同条件下Wu等［27，29，31］给出的结果一致。

4 结果分析与讨论

4.1 结果分析由式（18）和式（22）可以看出，河流岸边排放污染混合区边界归一化曲线的形状和面积系数，两者都只是参数p（=2+m-n）和q（=1+α）的函数。下面分别绘制污染混合区边界归一化曲线分类图谱和面积系数变化曲线族来做进一步分析。

首先，选择参数p=2、p＜2（以p=1代表）、p＞2（以p=4代表）和q=1、q＞1（以q=3代表），针对（p，q）的6种组合情况，由式（18）分别绘制污染混合区边界归一化曲线，见图3。图中，标准型、Ⅰ型、Ⅱ型分别对应（p=2，q=1）、（p＜2，q=1）、（p＞2，q=1）情况，此时α=0，污染混合区最大宽度对应的归一化纵向坐标Lc/Ls=1/e≈0.368；α-标准型、α-Ⅰ型、α-Ⅱ型分别对应（p=2，q＞1）、（p＜2，q＞1）、（p＞2，q＞1）情况，此时α＞0，污染混合区最大宽度对应的归一化纵向坐标Lc/Ls＞0.368。

其次，选择参数p=1.0，1.5，2.0，3.0，4.0和5.0，在参数q=1～5区间内取一系列值，采用式（24）或式（26）或式（27）分别计算污染混合区面积系数μ（p，q），给出以p为参数的面积系数μ（q）变化曲线族，见图4。

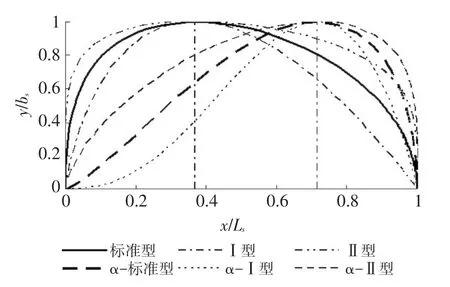
图3 河流岸边排放污染混合区边界归一化曲线分类图谱

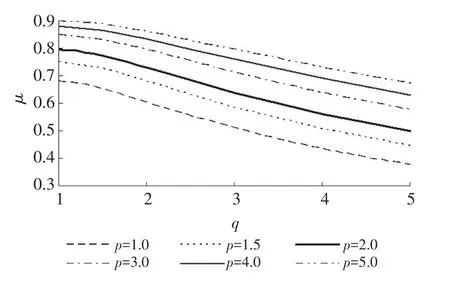
图4 河流岸边排放污染混合区面积系数变化曲线族

由图3和绘制条件可知，当参数q不变，参数p变化时，污染混合区边界归一化曲线最大宽度对应的归一化纵向坐标位置保持不变，只有污染混合区边界归一化曲线的形状随着参数p的增大，逐渐由尖瘦变为钝肥；而当参数p不变，参数q变化时，污染混合区边界归一化曲线最大宽度对应的归一化纵向坐标位置将随着参数q的增大，沿着流向逐渐偏离原来位置，其形状随之发生变化。

由图4可以看出，当参数p不变时，污染混合区的面积系数μ（q）为单调下降曲线，在q=1时的面积系数最大；当参数q不变时，污染混合区的面积系数随着参数p的增大而增加，这一点与污染混合区边界归一化曲线形状的分析结果一致。

通过以上分析，并注意到式（17）和式（18），可以得出的重要结论是:参数q值决定着污染混合区形状最大宽度对应的归一化纵向坐标位置，参数p值决定着污染混合区形状的丰满程度。

4.2 污染混合区的分类条件通过上述对河流岸边排放污染混合区边界归一化曲线分类图谱和面积系数变化曲线族的规律分析，发现:

当参数（p=2，q=1）时，对应河流流速和横向扩散系数均为常数（m=n=0）以及流速和横向扩散系数均服从横向指数分布（满足m=n）情况，这时的污染混合区形状定义为标准型；当（p＜2，q=1）时，对应流速和横向扩散系数横向分布（满足0＜m＜n）情况，定义为Ⅰ型；当（p＞2，q=1）时，对应流速和横向扩散系数横向分布（满足m＞n＞0）情况，定义为Ⅱ型。

当（p=2，q＞1）时，对应流速为常数，横向扩散系数仅随纵向坐标x呈指数变化（满足m=n=0、α＞0）以及流速和横向扩散系数均服从横向指数分布，同时横向扩散系数又随纵向坐标x呈指数变化（满足m=n、α＞0）情况，定义为α-标准型；当（p＜2，q＞1）时，对应流速和横向扩散系数分布（满足0＜m＜n、α＞0）情况，定义为α-Ⅰ型；当（p＞2，q＞1）时，对应流速和横向扩散系数分布（满足m＞n＞0、α＞0）情况，定义为α-Ⅱ型。具体描述，详见表1。

由表1可以看出，河流岸边排放污染混合区的形状与深度平均流速和横向扩散系数变化的特性参数（p=2+m-n，q=1+α），具有一一对应的关系。在表1分类中，河流岸边排放污染混合区的部分类型与已有研究特例的对应关系为:标准型与文献［26-27］、α-标准型与文献［29-30］、Ⅰ型和Ⅱ型与文献［31］中的研究条件和结果分别对应一致。表1给出的河流岸边排放污染混合区类别、形状特征与分类条件是科学探究从特殊性到普遍性的系列研究成果。该成果全面科学系统地反映了用于表征河流深度平均流速和横向扩散系数变化的特性参数（m，n和α）直接影响河流二维移流扩散污染物浓度分布规律和污染混合区几何形状特征的对应关系。

表1 河流岸边排放污染混合区类别、形状特征与分类条件

长期以来，寻找河流断面平均横向扩散系数（常数）的通常做法是根据横向浓度分布与断面平均水力学要素之间的关系，来建立基于常数的横向扩散系数经验公式。而忽视了对河流二维浓度分布和水力学要素的同步观测与综合分析，使得各自给出的横向扩散系数经验公式数量多，形式繁杂，各个公式的计算结果扑朔迷离［5］。其问题可能出在人们一直试图采用常数横向扩散系数来表征纵、横向变化的河流横向扩散系数。研究发现宽阔河流的中部深槽和远岸地形变化，对排放岸附近污染混合区的污染物输移扩散作用很小，因此在大江大河采用断面平均横向扩散系数是不合适的。

4.3 反问题：变横向扩散系数的估算方法河流岸边排放污染混合区边界几何特征尺度的理论公式和等浓度线方程，可以反向使用以便获得变横向扩散系数的具体表达式。该方法仅需要对岸边污染混合区边界曲线的宏观几何特征尺度和流速横向分布进行测量，为从业者提供现场使用的有效方法，在大江大河中非常实用。

首先，在拟观测的宽阔河流上，选择一个稳定的岸边排污口或排放点，在排水中以恒定速率均匀地投加无毒害有色荧光染料（如罗丹明B）溶液。岸边污染混合区中的染料浓度与颜色的阴影成比例，即有同色度线表示等浓度线。需强调的是，当河岸倾角小于28°时，水面与深度平均浓度近似相等，水面浓度分布可作为污染混合区的确定依据［33］。这种要求通常在天然河流中很容易得到满足。

其次，按照水文测量技术观测河流中的流速横向分布，采用式（1）拟合确定u1，y1和m的值。速度测量不需要覆盖整个河流，只需要覆盖形成污染混合区的近岸区域。

第三，采用无人机摄像装置，从上空拍摄岸边污染混合区的彩色图像资料。经导入计算机、图像筛选、坐标定位和图像处理，初步读取单条同色度线的最大长度Ls、最大宽度bs与对应的纵向坐标Lc。采用式（17）反推得到q的初值:

再对污染混合区边界（等浓度）曲线的形状，采用式（18）进行试错法拟合比较，最终确定出一条与该单条同色度线吻合程度较高曲线的最大长度Ls、最大宽度bs和参数p、q值，从而可以求出正常数指数n=2+m-p和α=q-1。进而采用式（16）反推出正常数系数γ:

最后，将γ，α，y1和n代入式（2）得到变横向扩散系数的具体表达式。

该方法的最大优点是无需测量排污量和浓度分布的具体数值，因为河流流速和横向扩散系数变化形式决定了污染混合区的不同形状，而排污量和浓度分布的具体数值主要是影响河流污染混合区的范围大小。

5 实例

下面根据黄真理等［28］在长江三峡建水库前库区水环境现状及水文水质污染负荷同步观测中，给出的黄沙溪排污混合区平水期同步观测资料，采用本文理论来估算该河段岸边排放的变横向扩散系数式（2）中的正常数参数和经验公式。

黄沙溪排污混合区平水期CODCr现场观测等值线与理论拟合曲线，参见图5。图中彩色渲染浓度部分摘自文献［28］，3条浓度等值线均由式（18）拟合而得。表2给出了黄沙溪排污混合区平水期CODCr=9.85、10.00和10.81 mg/L相应的等值线最大长度、最大宽度和其对应纵向坐标的观测值。经采用同一组参数（p，q）值和式（18）对图5中的3条浓度等值线分别进行理论拟合。结果表明，当参数（p=1.50，q=1.65）时，对应表1中的α-Ⅰ型污染混合区，Lc/Ls=0.545，面积系数μ=0.713，3条浓度等值线的总体吻合程度最好，并给出了3条CODCr等值线的最大长度、最大宽度和其对应纵向坐标的理论拟合值，见表2。

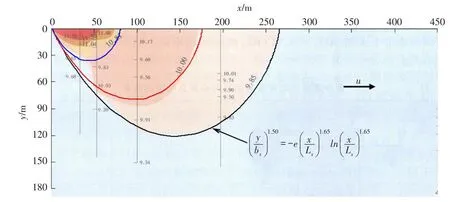
图5 黄沙溪排污混合区平水期CODCr现场观测等值线与理论拟合曲线

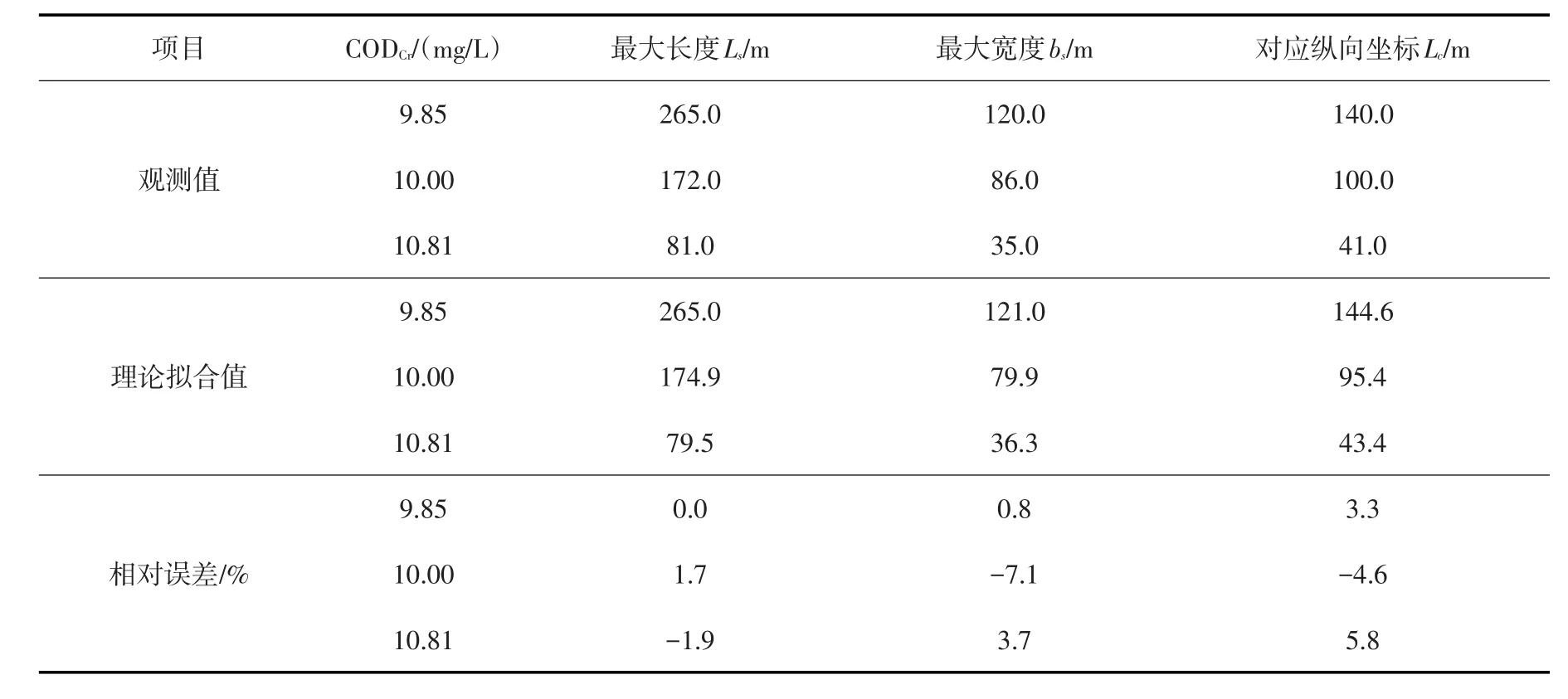
表2 黄沙溪排污混合区平水期CODCr等值线几何特征参数

由表2可以看出，黄沙溪排污混合区平水期3条CODCr等值线最大长度、最大宽度和其对应纵向坐标的理论拟合值与观测值的最大相对误差绝对值分别为1.9%，7.1%和5.8%，结合图5判断两者吻合良好。

基于2.1节中获得的黄沙溪排污混合段平水期深度平均流速横向分布式（1）中的有关参数:y1=150 m，u1=1.4 m/s，m=0.25，考虑到参数（p=1.50，q=1.65），求出正常数指数n=0.75和α=0.65。再根据黄沙溪排污混合区平水期3条CODCr等值线理论拟合的最大长度Ls、最大宽度bs和有关参数，采用式（29）分别计算出变横向扩散系数中正常数系数，从而得到其平均值γ=5.96。最后，将γ，α，y1和n代入式（2）得到长江黄沙溪排污混合区平水期的变横向扩散系数经验公式为:

式中物理量采用国际单位制。

长江黄沙溪排污混合区平水期深度平均流速和横向扩散系数的横向分布指数m、n之和恰巧等于1，这与Li［32］在低层大气扩散研究中，建议n值通常取为（1-m）一致。这是巧合还是有某种规律有待进一步深入研究。

需要说明的是:在野外水体中，虽然CODCr具有一定的降减能力，但根据文献［26］给出的判别条件，当降解数De=KLs/U≤0.027时，可以忽略反应降解作用，按保守物质计算污染混合区范围。如果取CODCr的较大降解系数K=0.4 d-1=4.63×10-6s-1，黄沙溪岸边区域的平均流速U≈1.0 m/s，当CODCr=9.85 mg/L时的污染混合区最大长度Ls=265.0 m，由此计算得到降解数De=KLs/U=0.0012≪0.027。所以，上述实例计算忽略反应降解作用是合理的。在文献［28］中，对于黄沙溪排污混合区CODCr浓度场的验证、污染混合区的模拟预测和实用化计算公式，同样忽略了CODCr的降解作用。

6 结论

（1）这项研究在宽阔河流顺直岸边稳定点源条件下，考虑深度平均流速的横向指数分布和横向扩散系数的二维变化关系，基于变系数二维移流扩散方程，推导了污染物浓度分布解析解，提出了污染混合区最大长度、最大宽度和对应纵向坐标以及面积的理论公式。

（2）给出了污染混合区边界归一化曲线方程。表明河流岸边排放污染混合区的形状与深度平均流速和横向扩散系数变化特性参数（p=2+m-n，q=1+α），具有一一对应的关系，提出了河流岸边排放污染混合区的类别、形状特征、分类条件和变横向扩散系数的估算方法。

（3）实例表明，α-Ⅰ型污染混合区能够较好地表征长江黄沙溪排污混合区平水期CODCr现场观测等值线形状。给出了黄沙溪深度平均流速和横向扩散系数变化特性参数以及排污混合区平水期的变横向扩散系数经验公式。

（4）研究发现宽阔河流的中部深槽和远岸地形变化，对排放岸附近污染混合区范围的影响很小。因此，在大江大河考虑河流流速和横向扩散系数的变化特性非常必要，应引起河流污染混合区几何特征计算和水质建模工作者的高度重视。