基于向量地震动强度指标的拱坝地震易损性分析

范书立，田 硕，陈健云

（海岸与近海工程国家重点实验室 大连理工大学，辽宁 大连 116023）

1 研究背景

我国西南强震区拥有我国约80%的水能资源，在这些地区建设高坝大库很难避让大坝结构抗震安全问题，高坝在地震中一旦溃坝将对下游地区造成严重的次生灾害［1-2］。强震区建设的高坝设防烈度大，地基条件复杂，面临着许多重大关键技术问题的挑战，所以需要采用合理的方法评价高坝的抗震安全性能［3-4］。大坝地震易损性分析可以预测不同强度地震作用下大坝发生不同等级破损的概率，从而可以为基于性能的大坝抗震安全评价与决策提供科学依据［5］。因此，研究地震易损性对于强震区高坝的抗震设计、合理判断其抗震能力具有十分重要的意义。

Ellingwood等［6-7］将易损性分析方法引入到水工结构领域，对美国某混凝土重力坝进行了不同洪水水平下以及不同地震水平下的易损性分析。沈怀至等［8］通过调整12条地震波的峰值加速度，建立了金安桥重力坝-地基系统的易损性曲线，提出了大坝-地基系统整体的易损性评价方法。钟红等［9］在考虑混凝土材料细观非均匀性的基础上，分析了金安桥重力坝的易损性，得到了以地震动峰值加速度为变量的大坝易损性曲线。姚霄雯等［10］以拱坝拱冠最大位移为响应量定义了3个性能水准，结合结构反应回归分析得到的概率地震需求模型，建立了基于拱冠位移的易损性曲线。李浩瑾等［11］以地震动峰值加速度为变量建立了最小二乘支持向量机模型，结合Monte Carlo仿真分析对大坝动力稳定性进行了易损性分析。Kadkhodayan等［12］以坝面超应力面积为响应量，以谱加速度、峰值加速度和峰值速度为地震动强度指标，分别进行增量动力分析，通过拟合增量动力分析结果定义性能水准，建立了易损性曲线。马智勇等［13］通过调整地震动峰值加速度进行不同水平的标准化，采用增量动力分析研究了位移和坝体损伤破坏形态之间的相关性，结合SAC-FEMA方法提出了重力坝的易损性分析方法。Wang等［14］考虑多个响应量分别采用Monte Carlo方法和增量动力分析方法建立了大岗山拱坝的地震易损性曲线。上述大坝地震易损性分析中均是采用标量形式的地震动强度指标（intensity measure，IM），即以单个地震动强度指标建立易损性曲线。但是由于地震动所包含信息的复杂性，采用标量IM忽视了其它地震动强度信息，不能较好的表征地震动特性，会导致对结构的需求估计存在较大的离散性［15］。

针对标量IM存在的问题，Baker等［16］提出了一个向量地震动强度指标，能够考虑结构第一阶周期对应的地震动反应谱值以及反应谱形状对结构动力反应估计的影响。Seyedi等［17］基于向量IM建立了框架结构的地震易损性曲面，降低了框架结构响应预测的离散度。Gehl等［18］采用向量IM对某框架结构进行了易损性分析，研究了峰值加速度、速度、不同周期谱加速度、震级、持时等组合情况下结构的地震易损性曲面，分析了结构的抗震性能。Li等［19］采用基于向量IM的地震易损性曲面对钢筋混凝土桥墩进行了易损性分析，对不同损伤状态下桥墩的易损性进行了研究。Alembagheri［20］研究了不同向量IM在重力坝地震需求评估中的应用，比较了不同的向量IM的效率。陈力波等［21］采用受试者工作特性分析方法选取了有效性较好的两个地震动强度指标，建立了双地震动强度指标的桥墩易损性模型。向量IM考虑了多个反应地震动强度的指标，因此它与标量IM相比能够更加充分地描述地震动的不确定性，在进行结构风险分析时能够考虑地震动强度参数不确定性的影响。

本文选取20条地震动，将混凝土抗压强度、地基弹性模量和阻尼比作为随机材料参数，以拱冠顺河向最大相对位移、拱冠横缝最大开度和坝体损伤体积比为性能指标，以地震动顺河向分量的一、二阶谱加速度和地震动横河向、顺河向分量的一阶谱加速度分别作为向量地震动强度指标，对白鹤滩拱坝进行地震易损性分析，建立基于向量IM的易损性曲面，提出了基于向量IM的拱坝地震易损性分析方法，为高混凝土拱坝的抗震安全评价及风险评估提供参考。

2 基于向量IM的结构地震易损性分析方法

结构响应与向量IM=（IM1，IM2）之间满足线性关系［16］:

式中:R′为拟合的结构响应；a、b、c为拟合系数；IM1、IM2为向量IM中的两个强度参数。

结构地震易损性描述了结构在某一强度地震作用下响应超过性能水准的概率，通常采用对数正态累积分布函数描述，基于向量IM的易损性函数可表示为［16］:

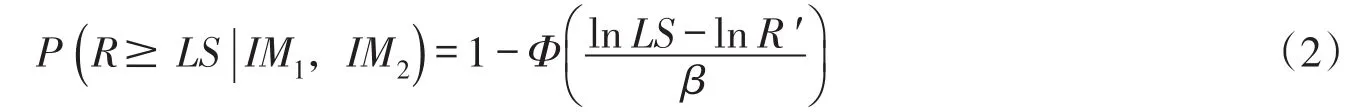
式中:R为结构的响应；LS为结构性能水准，是结构处于不同破坏状态时结构响应的界限值，本文采用拱冠位移、横缝开度和损伤体积作为表示拱坝性能水准的指标，其取值在5.1节详述；Φ()⋅为标准正态累积分布函数；β为结构响应的对数标准差，计算公式为:

式中:Ri为第i次结构有限元分析得到的响应；n为结构瞬态分析的次数。

将式（1）和性能水准代入到式（2）中，即可得到基于向量IM的结构地震易损性曲面。

3 拱坝有限元模型和不确定性分析

3.1 拱坝有限元模型本文以白鹤滩拱坝为例进行计算分析。白鹤滩拱坝是非对称双曲拱坝，最大坝高289.0 m，坝顶高程834.0 m，上游正常蓄水位825.0 m，相应下游水位604.0 m。坝址区地震基本烈度为Ⅷ度，按100年基准期内超越概率2%的水准设防，相应的基岩水平峰值加速度为0.325g。按照100年基准期内超越概率1%的水准进行校核，相应的基岩水平峰值加速度为0.420g。除坝肩有少数六节点棱柱体单元外，坝体和地基均剖分成八节点六面体等参单元。参考文献［22-23］中采用的拱坝计算模型，本文沿坝体厚度方向剖分4层单元，从而能够观察到沿厚度方向的损伤扩展。拱坝的横缝在强震作用下会发生张开、闭合现象，横缝的张开使拱坝在强震作用下避免出现较大的拱向应力，内力由拱向向梁向分配传递。白鹤滩拱坝设计有30条横缝，根据其他学者对白鹤滩拱坝抗震分析的研究成果［24-25］，本文白鹤滩有限元模型简化模拟了13条坝体横缝，拱冠处的横缝间距为48.0 m。地基为辐射状，外围设置一层无限元，模拟无限地基的辐射阻尼。白鹤滩拱坝有限元模型如图1所示。模型包括了两种非线性:考虑混凝土损伤的材料非线性和考虑横缝开合的接触非线性。混凝土损伤破坏力学特性采用混凝土损伤塑性本构模型模拟［26］。横缝采用考虑键槽咬合作用的接触模型模拟，忽略两接触面之间的切向滑移，只考虑横缝的张开闭合。计算荷载考虑了坝体自重、正常蓄水位时静水压力以及地震荷载，动水压力采用Westergaard附加质量模型模拟。对白鹤滩拱坝进行模态分析，获得拱坝顺河向第一、二阶频率分别为1.14 Hz、1.93 Hz；拱坝横河向一阶频率为1.30 Hz。

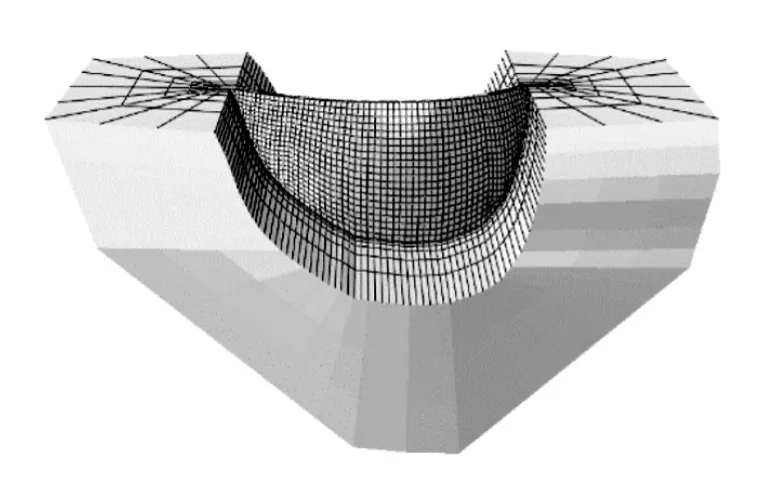
图1 拱坝有限元模型

图2 地震波放大系数谱

3.2 地震动及材料的不确定性地震动和材料的随机性会导致结构响应的离散性，所以结构地震易损性分析时应考虑二者的随机性。本文依据工程场地条件选取大量的实际地震动记录，通过实际记录的不同来反应地震动的不确定性。匹配水工建筑物抗震设计规范的设计反应谱，排除近场脉冲地震动，从美国太平洋地震工程研究中心强震数据库中选取20条地震动记录，具体选择参数为:震级4.5～8.0级，震中距10～100 km，剪切波速Vs＞500 m/s。地震动记录的信息如表1所示。

各条地震波在阻尼比为5%时的放大系数谱如图2所示。由图2可知，选取的20条地震记录的平均放大系数谱与规范设计反应谱基本一致，能够应用于拱坝易损性分析。20条地震记录顺河向分量在拱坝顺河向第一、二阶周期的放大系数分布如图3（a）所示，20条地震记录横河向分量在拱坝横河向一阶周期处的放大系数分布如图3（b）所示。

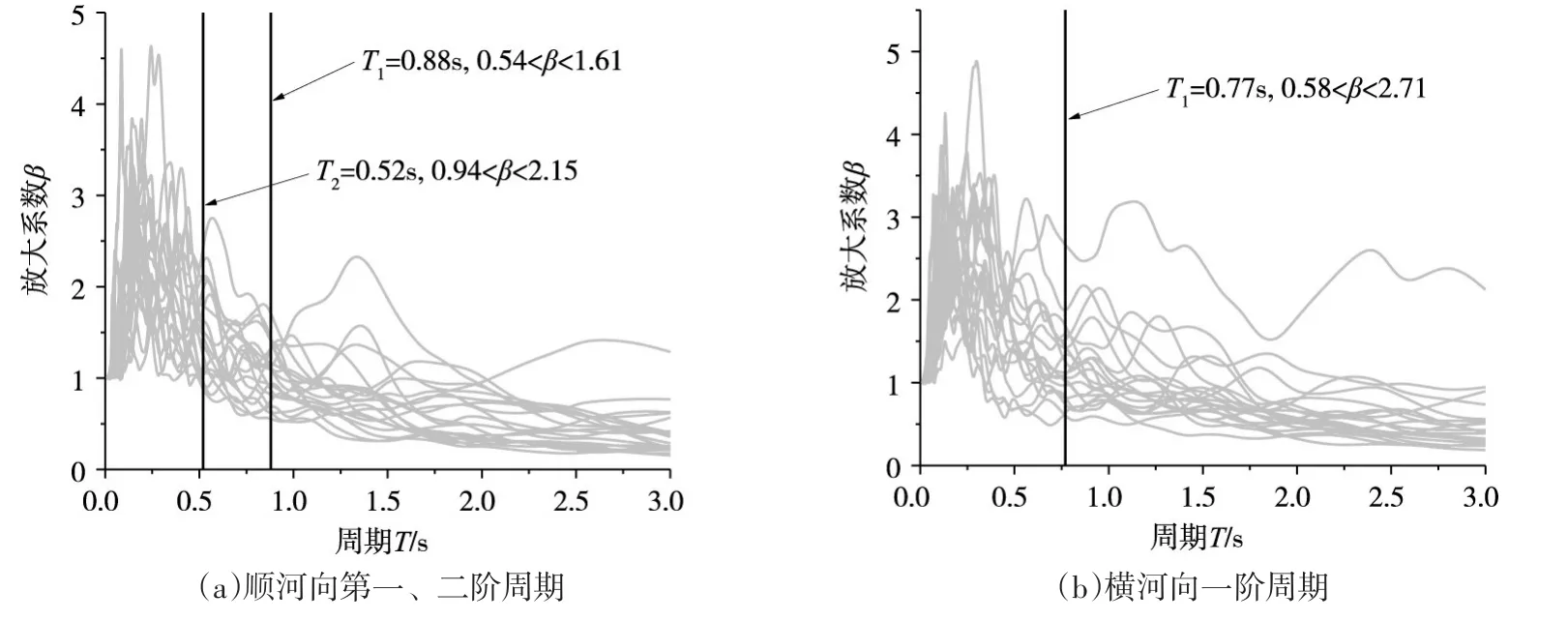
图3 放大系数分布

拱坝坝体的不确定性主要来源于混凝土材料的变异性，从而导致坝体地震响应的不确定性。本文考虑混凝土强度的变异性，将混凝土抗压强度假定为随机变量，抗拉强度取为0.1倍的抗压强度。考虑到有限元模型中地基按均质材料处理，为反应地基材料的变异性对拱坝响应的影响，将地基弹性模量视为随机变量。同时，将拱坝-地基系统阻尼比假定为随机变量。混凝土抗压强度、地基变形模量服从正态分布，阻尼比服从均匀分布［8］。根据《水电工程水工建筑物抗震设计规范》（NB 35047-2015），混凝土动抗压强度均值比静抗压强度均值提高20%，取为27.5 MPa，变异系数为0.16。地基弹性模量均值为19.5 GPa，变异系数为0.2。阻尼比变化范围为3%～7%。不考虑3个随机变量的相关性，采用高效的拉丁超立方抽样法对这3个随机变量进行抽样，获得5组材料样本，如表2所示。编号1～4的地震动记录与第一组材料结合，编号5～8的地震动记录与第二组材料结合，依次类推，形成拱坝有限元计算样本。

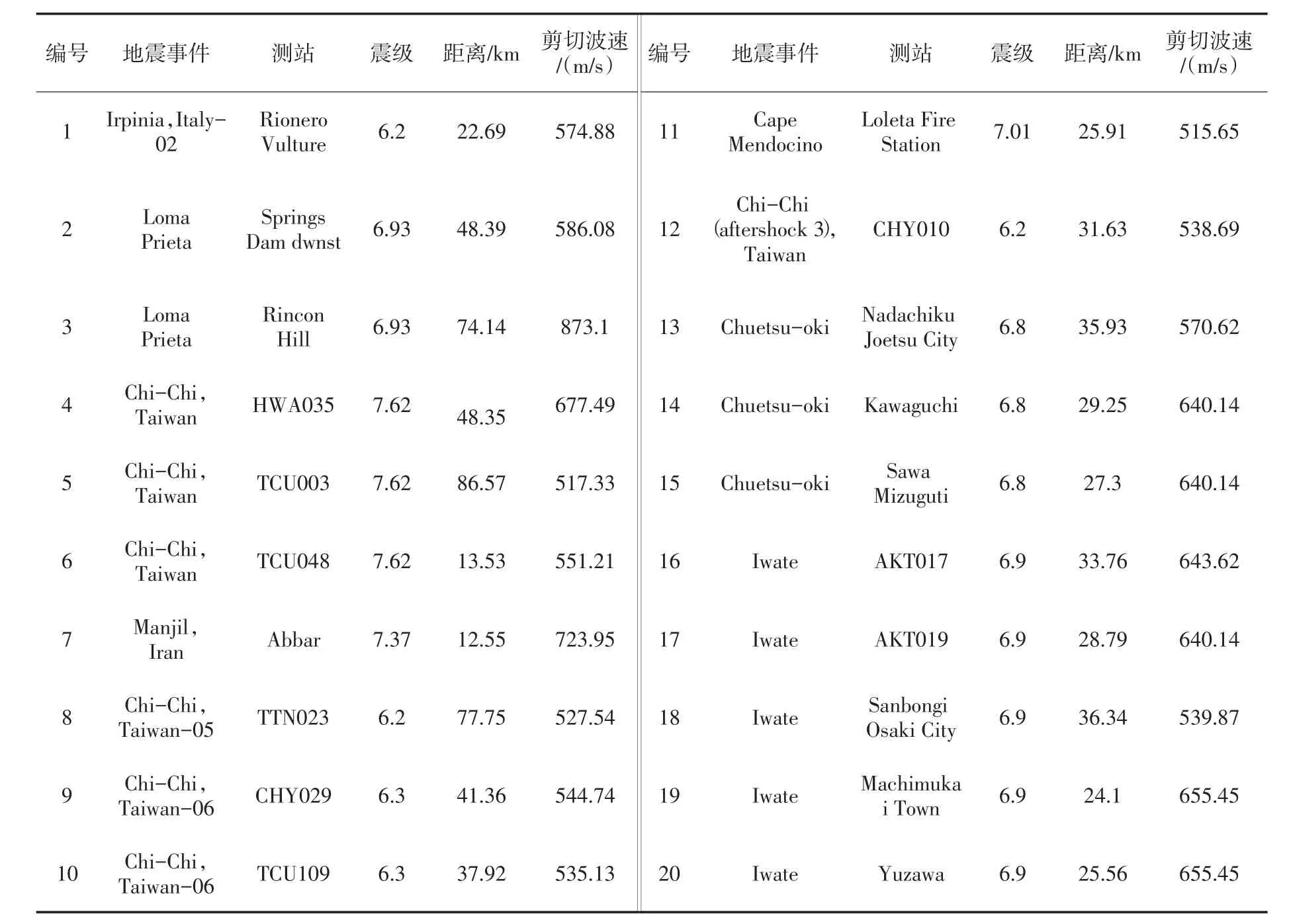
表1 地震动记录的信息

表2 材料样本

4 拱坝增量动力分析

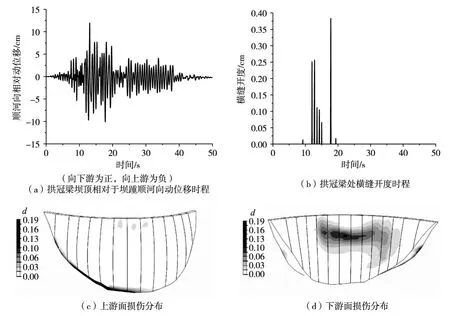
图4 设计地震动水平下的响应

4.1 设计地震水平下拱坝的动力反应分析对编号3地震动记录和第一组材料组成的有限元计算样本，在设计地震动水平下的拱冠梁坝顶相对于坝踵顺河向动位移时程、拱冠梁处横缝开度时程和损伤分布如图4所示。由图4可见，拱冠梁坝顶相对于坝踵最大顺河向动位移为11.95 cm（向下游），拱冠梁处最大横缝开度为0.39 cm；拱坝上游面损伤主要发生在左侧坝基、坝肩处，损伤因子分布在0.1～0.2；拱坝下游面损伤主要发生在中上部区域，损伤因子分布在0.1左右。

4.2 性能指标和向量地震动强度指标的选取本文选取拱冠梁坝顶相对于坝踵最大顺河向位移D、拱冠横缝最大开度C以及坝体损伤体积比DVR作为拱坝的抗震性能指标，其中坝体损伤体积比指的是坝体损伤体积（各单元的体积乘以单元损伤因子再求和）与坝体体积之比，可以表征拱坝整体损伤程度［27-28］。

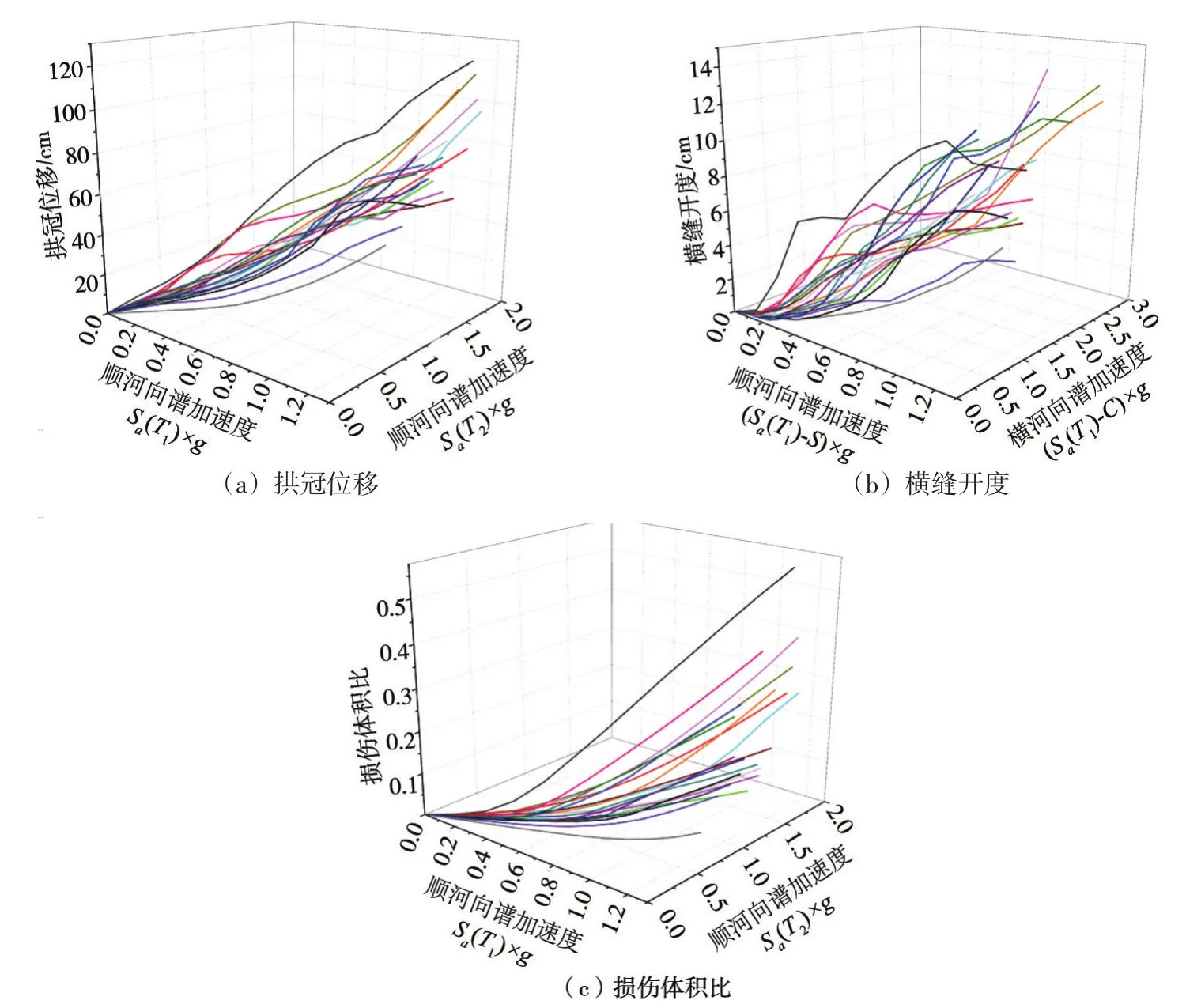
图5 增量动力分析曲线簇

对于拱冠位移，本文主要考虑地震动顺河向分量的影响。拱冠梁在强震作用下发生很强的非线性反应，所以选择向量地震动强度指标时需将非线性的影响考虑在内，根据文献［29］建议的方法，地震动强度指标选为地震动顺河向分量的一阶和二阶谱加速度，即向量IM=(Sa(T1)，Sa(T2))。对于横缝开度，除地震动顺河向分量外，横河向分量的影响也比较大，所以地震动强度指标选为顺河向谱加速度Sa(T1)-S与横河向谱加速度Sa(T1)-C，即向量IM=(Sa(T1)-S，Sa(T1)-C)。对于损伤体积比，拱坝损伤最为严重的下游面中上部区域主要受到地震动顺河向分量的影响，地震动强度指标选为地震动顺河向分量的一阶和二阶谱加速度，即向量IM=(Sa(T1)，Sa(T2) )。

4.3 增量动力分析结果以拱坝基本周期所对应的地震动顺河向分量加速度反应谱的谱加速度为调幅参数，将每条地震动在0.1g～1.2g之间连续调幅，间隔为0.1g，每条地震动的3个分量同时乘以相同的调幅系数，以保持比例关系不变。对于所选择的20条地震动共需进行240次非线性有限元动力时程计算，按照前述性能指标和向量地震动强度指标整理计算结果，如图5所示。

5 基于向量IM的拱坝地震易损性分析

5.1 性能水准定义通过大量的拱坝地震时程计算，从损伤破坏过程中直观的统计出拱冠位移、横缝开度和损伤体积比这3个性能指标与拱坝破坏等级之间的定量关系。随着地震强度的增加，拱坝典型破坏模式为坝踵坝肩先开裂，然后下游坝面中上部开裂，最后裂缝贯穿坝体。将坝基坝肩处起裂（损伤因子大于0.75可认为混凝土开裂［22］）、坝体下游面中上部区域起裂和裂缝贯穿整个坝体分别视为进入轻微、中等和严重破坏阶段的标志，根据损伤开裂云图统计每条地震动作用下大坝达到轻微、中等和严重破坏时的性能指标值，将20条地震动达到各破坏阶段的性能指标值取平均作为性能指标界限值，详细等级区分标准如表3所示。

表3 性能指标界限值

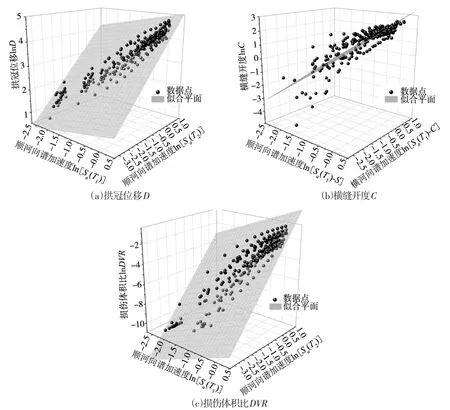
图6 概率地震需求模型

5.2 地震易损性曲面的建立将拱冠位移D、横缝开度C和损伤体积比DVR的增量动力分析结果分别取对数进行二元线性回归，得到概率地震需求模型，如图6所示。各概率地震需求模型的回归方程见表4。

表4 各概率地震需求模型的回归方程

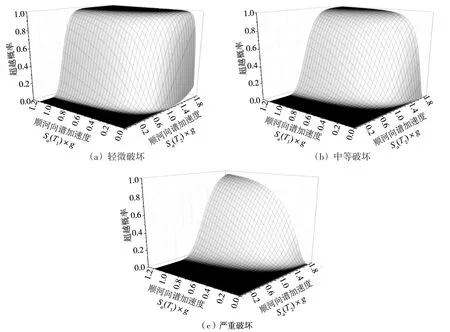
图7 拱冠位移的易损性曲面

把地震需求模型代入到计算易损性曲面的式（2）中，结合相应的性能指标界限值，即可得到地震易损性曲面。基于向量IM建立的拱冠位移、横缝开度和损伤体积比这3个性能指标的不同破坏等级的易损性曲面分别如图7—9所示，由得到的地震易损性曲面可以预测拱坝在不同强度等级地震作用下发生各级破坏的概率。

在设计地震动和校核地震动水平下，依据不同性能指标得出的拱坝各级破坏概率如表5所示。由表5可知，白鹤滩拱坝具有较高的抗震安全裕度。由于向量IM包含了两个地震动强度指标，得到的易损性曲面可以有效地反映不同地震动强度指标引起的拱坝失效概率的变化，为大坝的抗震设计、维修加固和风险评估提供更合理的理论依据。

由于向量IM的两个参数之间具有很强的相关性，所以易损性曲面自变量的有效取值范围并不是整个平面，需根据5.3节合理确定。

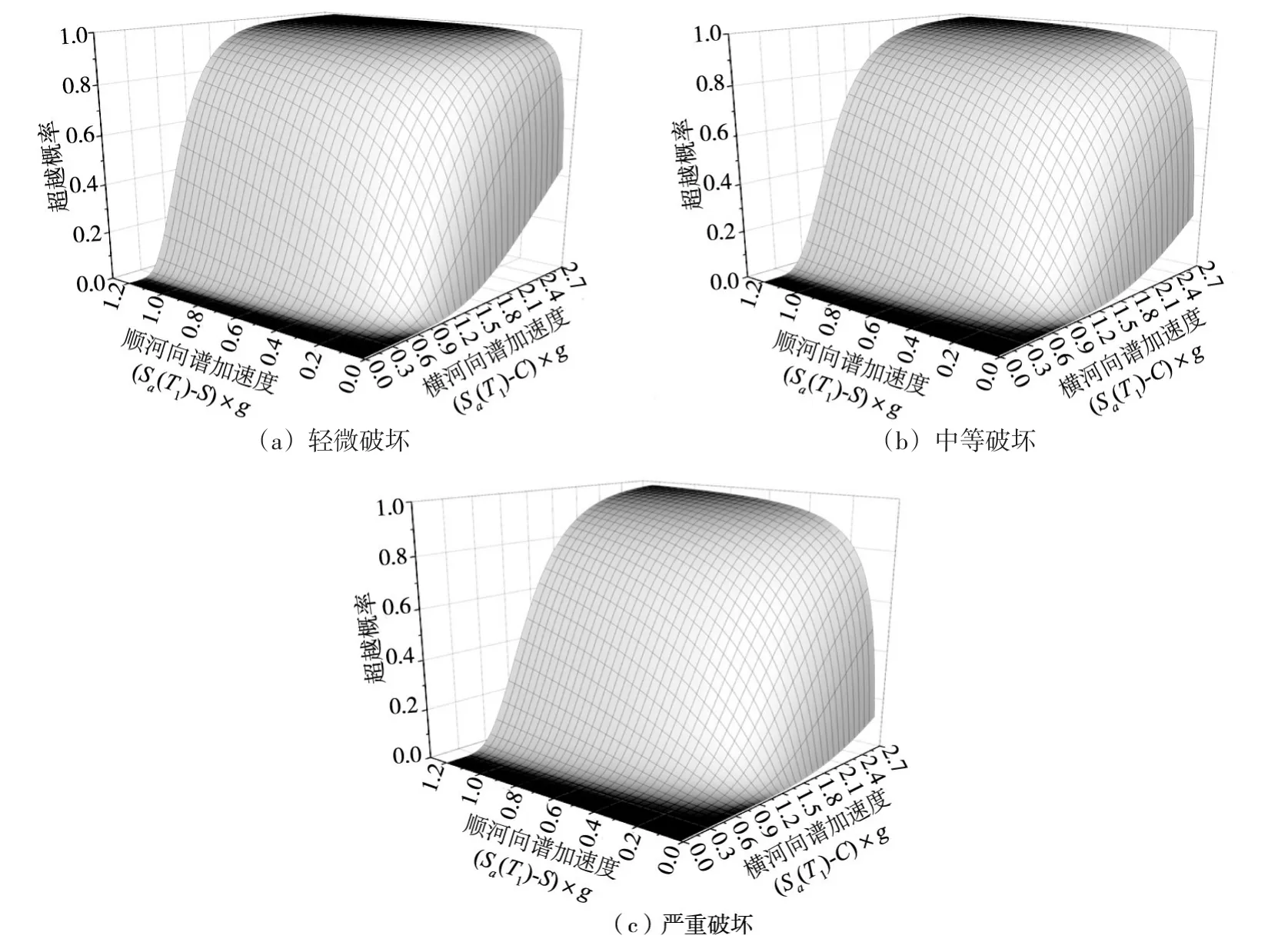
图8 横缝开度的易损性曲面

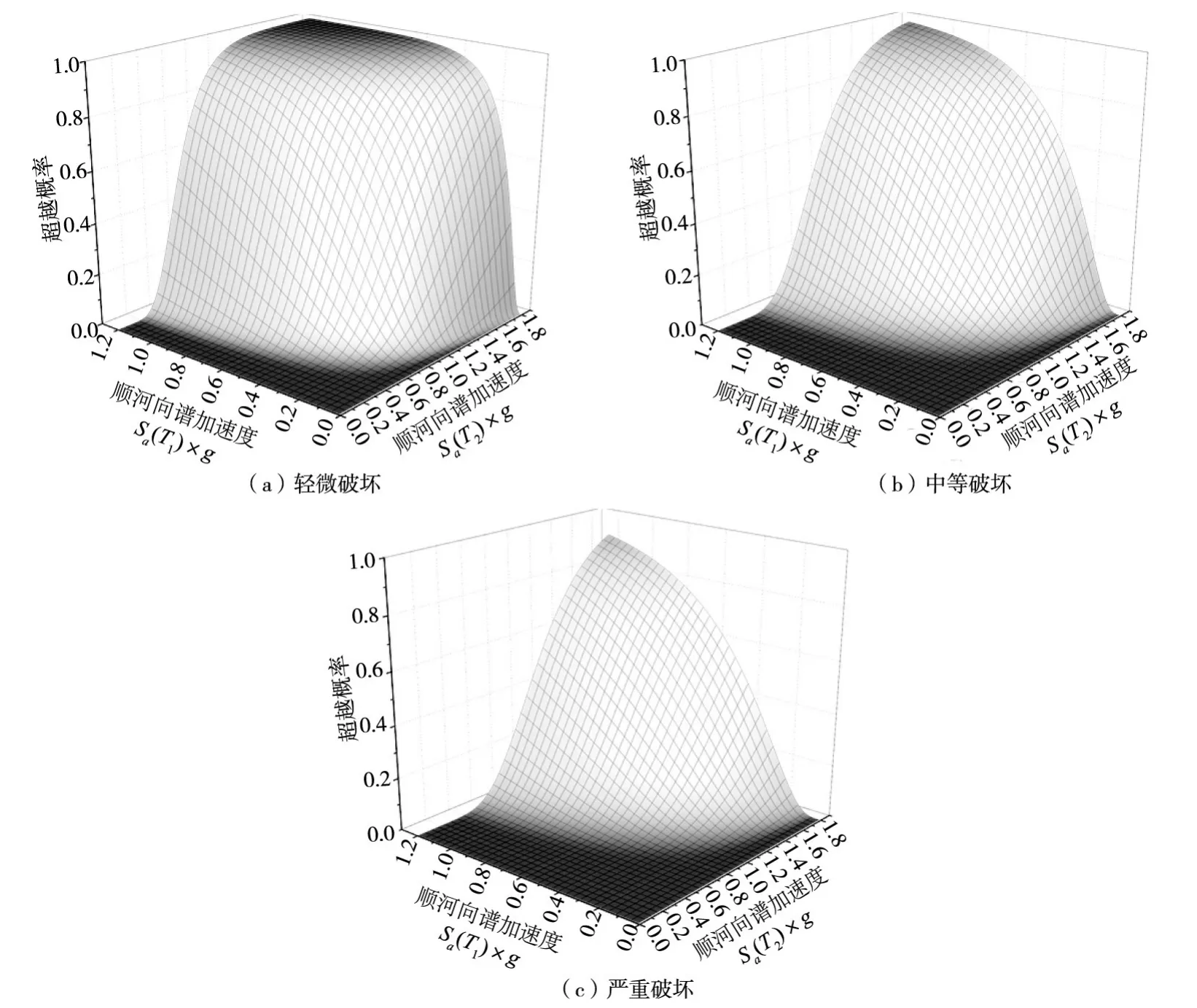
图9 损伤体积比的易损性曲面

5.3 易损性曲面自变量取值范围根据文献［18］提出的相关联向量IM的处理方法，本文采用统计学置信区间来确定易损性曲面自变量的有效取值范围。

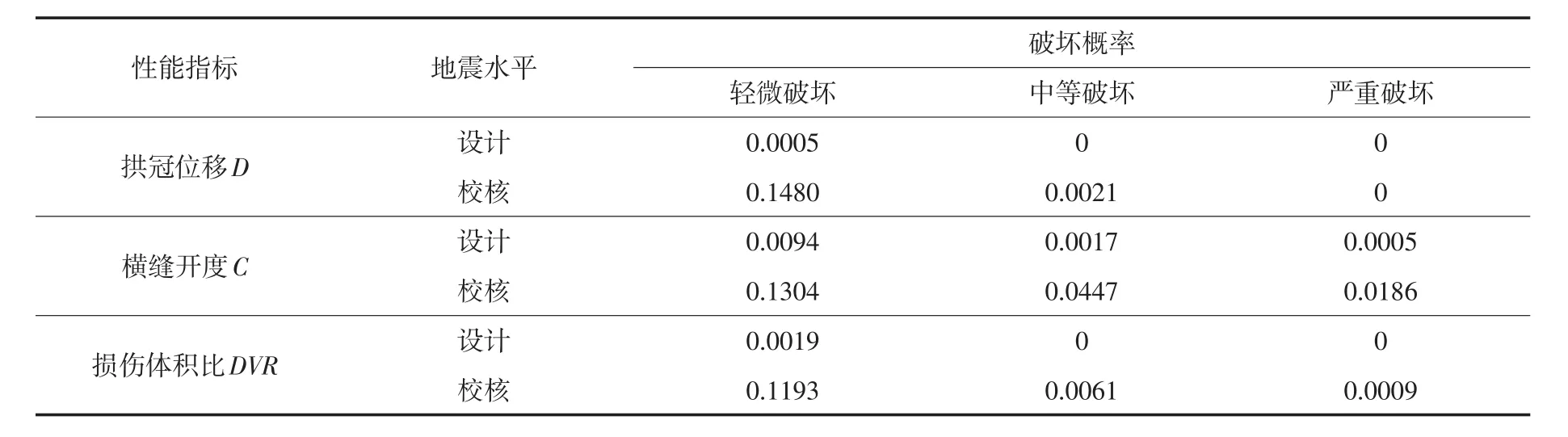
表5 设计和校核地震水平下拱坝破坏概率

对地震动强度指标顺河向谱加速度向量IM=(Sa(T1)，Sa(T2))的两个参数进行线性回归分析，取置信水平为95%的置信区间所围成的区域为向量IM的有效区间，如图10所示。对地震动强度指标横河向与顺河向谱加速度向量IM=(Sa(T1)-S，Sa(T2)-C) 进行相同的处理，结果见图11。

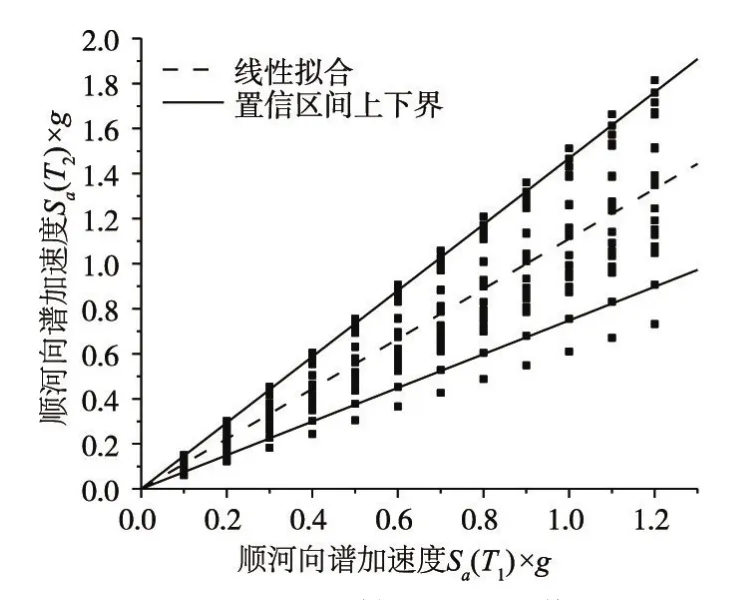
图10 顺河向谱加速度的取值范围

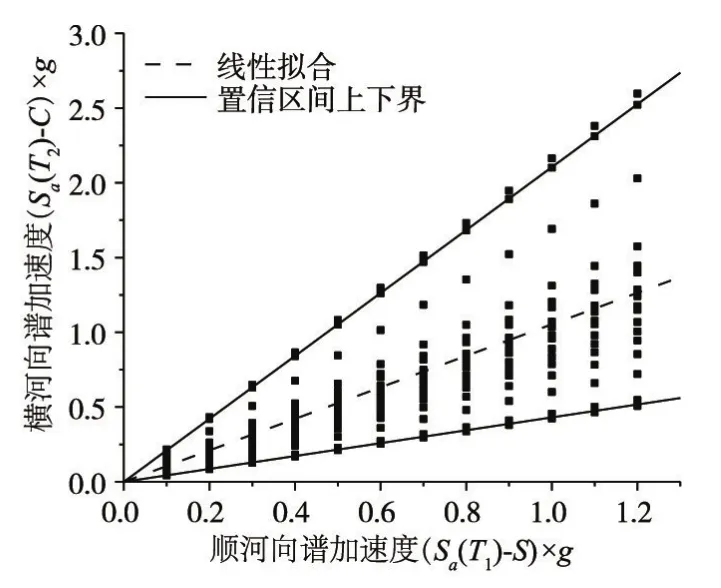
图11 横河向与顺河向谱加速度的取值范围

5.4 向量IM和标量IM的比较地震动强度指标最重要的特性就是它的效率，效率高的强度指标可以降低结构地震需求预测的离散性，由高效强度指标建立的地震易损性曲线也就更加合理。评价地震动强度指标是否高效可以采用拟合的概率地震需求模型的残差平方RSS和和线性相关系数R2。残差平方和越小，强度指标越高效；线性相关系数越接近于1，强度指标越高效。对拱冠位移D、横缝开度C和损伤体积比DVR这3个性能指标，对比向量IM和标量IM的效率，向量IM如前文所定义，标量IM选为地震动顺河向分量的一阶谱加速度，对比结果如表6所示。由表6可知，对于性能指标横缝开度C，向量IM在值上优于标量IM，但是在值上不如标量IM。对于拱冠位移D和损伤体积比DVR这两个性能指标，向量IM均比标量IM更加高效。拱冠位移D和顺河向谱加速度向量IM=(Sa(T1)，Sa(T2))的组合方式最为高效。

表6 向量IM和标量IM的比较

6 结论

本文将地震动顺河向分量的一、二阶谱加速度以及地震动横河向、顺河向分量的一阶谱加速度分别作为向量地震动强度指标，建立了白鹤滩拱坝拱冠位移、横缝开度和损伤体积比这3个性能指标的不同破坏等级的地震易损性曲面，并对易损性曲面自变量取值范围进行了研究，对比分析了向量IM和标量IM的效率，得到以下结论:（1）向量IM的两个参数具有很强的相关性，在建立地震易损性曲面时要考虑这个因素，合理地确定易损性曲面自变量取值范围。（2）对于不同的拱坝性能指标，基于向量IM建立的地震易损性曲面降低了拱坝地震需求预测的离散性，提高了预测精度，能够更高效地评估拱坝的抗震性能。拱冠位移D和顺河向谱加速度向量IM=(Sa(T1)，Sa(T2))的组合方式最为高效。（3）由于向量IM包含更多的地震动强度信息，基于向量IM建立的地震易损性曲面可以有效地反应由多个强度参数引起的拱坝失效概率的变化，能够更加准确地对拱坝的抗震性能作出评估。基于本文方法给出了在设计地震动和校核地震动水平下，依据不同性能指标得出的白鹤滩拱坝各级破坏概率。

本文在选取拱冠位移和损伤体积比这两个性能指标的向量地震动强度指标时，考虑了地震动顺河向分量的一阶和二阶谱加速度。当拱坝在强震作用下产生很强的非线性反应时，更高阶周期对应的谱加速度可能也是反映地震动强度的一个有效参数，所以建立包括更高阶谱加速度在内的多维向量地震动强度指标将是笔者下一步重点研究的内容。