考虑法向初始抗拉强度和切向抗剪强度变化的拱坝横缝模型研究
牛智勇,胡志强,林 皋
(大连理工大学 建设工程学部,辽宁省大连市 116024)
考虑法向初始抗拉强度和切向抗剪强度变化的拱坝横缝模型研究
牛智勇,胡志强,林 皋
(大连理工大学 建设工程学部,辽宁省大连市 116024)
拱坝横缝在灌浆后保证了坝体的整体性,横缝中的灌浆体具有一定抗拉强度,且球形、梯形键槽对切向滑动的约束与横缝张开度相关。本文在B-可微方程组形式的横缝接触模型基础上,针对法向、切向约束条件进行了修正,提出了考虑横缝初始抗拉强度、键槽切向抗剪力与张开度相关的修正接触模型。数值试验表明,该模型能够模拟拉应力通过横缝在坝块之间传递,以及在横缝张开时,键槽仍能提供较大的切向约束力。
拱坝;横缝;初始抗拉强度;键槽
0 引言
拱坝是作为整体结构来承受水、砂和温度等荷载等作用的,但在施工过程中,为防止坝体混凝土受温度荷载影响产生裂缝,需采用分块浇筑,在各块之间设置横向收缩缝的施工措施,待坝体混凝土冷却到年平均气温,混凝土充分收缩后,再用压力灌浆封拱。但横向收缩缝的存在降低了拱坝的整体性,实际工程中在横缝内设置键槽,以提高坝体的抗剪强度[1]。拱坝接缝处的抗拉强度较低,在温降、强震作用下横缝可能会发生张开、闭合及滑动的现象。这种现象将对拱坝的变形、应力等工作形态运行一定的影响。美国Pacoima拱坝在1971年San Fernando地震和1994年Northridge地震中,坝体横缝均发生张开,大坝在加固后仍可正常工作。美国加州大学Clough等人在拱圈地震激励试验中也观察到横缝在动荷载下出现“时开时合”的现象[2]。同时数值试验结果也表明[3],与整体坝模型相比,这种横缝张合现象将降低坝体中上部的拱向拉应力,对坝体地震响应产生重要影响。横缝的变形和受力过程看作是摩擦接触现象,使得坝体响应呈现非线性特性。基于横缝的几何、变形特性,学者们在横缝计算模型方面进行了深入的研究。Dowling[4]采用了二维两节点非线性弹簧模型; Fenves[5]、徐艳杰[3]采用的是三维接触单元模型;杜修力、涂劲[6],林皋、胡志强[7],赵兰浩[8]等人采用是的接触力学模型,包括:动接触模型[9]、非光滑方程组模型[10]、有限元混合法模型[11]。在接触本构方面,对于法向,大多采用接触力为压力的假定,在切向常采用库伦摩擦定律或者切向约束无限大的假设。在求解方法方面,常采用“试验-误差”迭代法、数学规划方法。上述研究工作一般假设缝面为平面,除文献[8]外,大多没有考虑横缝法向初始抗拉强度的影响,而在切向,常假定键槽仅在横缝闭合时才具有较强的抗剪能力,当横缝张开后其切向约束作用则不再有效。然而,对于实际拱坝工程,横缝灌浆后也具有一定的抗拉强度,可以在一定程度上承受拱向拉应力,并对两侧坝块的应力分布产生一定的影响。另一方面,横缝一般采用矩形、梯形和球形键槽来约束坝块之间的切向运动,提高坝体的整体性。近年来,我国高拱坝建设常采用球形键槽,具有可避免应力集中、施工方便的特点。其中,采用梯形或球形键槽的横缝张开时,只要张开度小于键槽高度,键槽仍具有抗剪切能力,且抗剪强度并不是常数,而是与横缝张开度相关。
本文基于摩擦接触条件的B-可微方程组表示形式,对其进行修正,提出了能够考虑拱坝横缝初始抗拉强度和键槽切向约束作用随横缝开度变化的接触模型。
1 考虑初始抗拉强度和键槽约束变化的横缝接触模型
1.1 弹性摩擦接触问题的B-可微方程组方法[12]
下面对弹性摩擦接触问题的B-可微方程组解法作简单介绍。
本文采用小变形、小位移假定,因此可采用点-点接触模型,即横缝两侧坝块节点一一对应。对于两体(分别用体1和体2来表示)接触情形,在接触点对处,定义局部坐标系nab,其中表示接触面的法向,由体2指向体表示接触面上互相垂直的两个切向单位向量。Pn、Pa、Pb表示局部坐标系下接触点对的接触力。假设接触系统中,总的接触点对个数为NC。对于三维弹性摩擦接触问题,每个接触点对i处的接触条件可表示成如下的B-可微方程组形式:
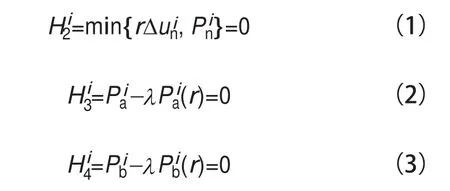
其中,

式(1)表示法向接触条件,包括法向不能互相嵌入以及法向接触力为压力的条件,这里假定接触表面的压力为正值,拉力为负值;法向张开为正值,法向嵌入为负值。式(2)和式(3)表示切向接触条件,这里我们假定切向运动服从库仑摩擦接触条件,即:滑动时,切向接触力大小等于法向接触力乘以摩擦系数滑动方向与切向接触力方向在一条直线上且方向相反;无相对滑动时,切向接触力小于法向接触力乘以摩擦系数
1.2 考虑横缝初始抗拉强度和键槽约束作用变化的修正B-可微方程组接触模型
横缝灌浆后,砂浆仍具有一定的抗拉强度,可以在相邻坝块之间传递拉应力,这就使得横缝间的接触力可能出现拉力的情形,为此,法向接触条件式(1)可修改成下面的形式:
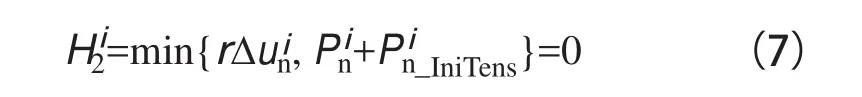
为了反映键槽抗剪能力与横缝张开度相关,可将式(6)修改为下式的形式:
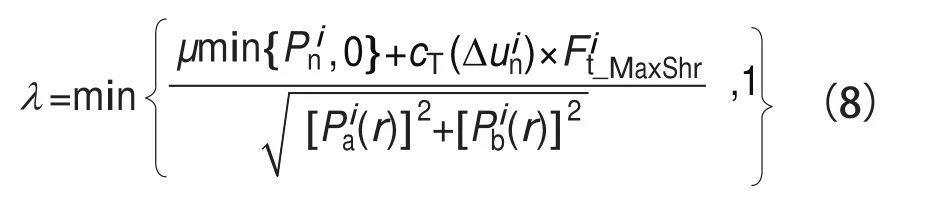
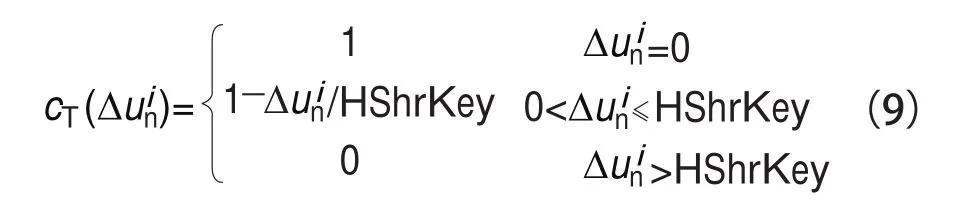
由式(8)可见,当横缝闭合时,切向抗剪力由两部分组成,一部分为摩擦力,一部分为键槽引起的抗剪力;当横缝张开时,若张开度小于横缝键槽高度,则切向剪力仅由键槽产生,若张开度大于横缝键槽高度,切向剪力为0。
1.3 修正B-可微方程组接触模型的求解
除了上述接触条件H2=0,H3=0和H4=0,对于接触问题的求解,还需要整体结构的平衡方程,如下式所示:

其中,K表示结构的刚度阵;u表示位移;R表示外荷载;P;表示接触力,其中,u和Pc为未知量。
这样,平衡方程和接触方程就构成了弹性摩擦接触问题的数学模型:
(5)可靠性原则。系统应满足电网企业运营监测业务应用24小时可靠运行的要求,系统关键环节软硬件资源设计采用高可用方案,保证系统运行的高度可靠,避免出现数据不及时和信息失真等现象。

在求解上述方程组时,H1的方程数为结构的总自由度个数,H2~H4的方程总数为3NC,其中NC为接触点对的个数。假设坝体为线弹性材料,为了提高求解效率,可先利用平衡方程求解出接触柔度阵,即接触力和接触点对相对位移之间的关系,记做矩阵F,然后再利用接触柔度阵F求解接触方程组,求出接触力,最后,将接触力代入到平衡方程中,求出结构位移u。
对于接触条件所形成的B-可微接触方程组或修正的B可微方程组,均可采用B-可微阻尼牛顿方法求解,该方法具有较好的全局收敛特性,具体解法可见参考文献[13]。本文采用有限元软件ANSYS建立拱坝有限元离散模型,根据上文介绍的横缝计算模型采用Fortran语言编制了拱坝横缝计算程序进行计算。
2 工程算例
某双曲拱坝坝高210m,设置横缝27条,如图1所示,坝体有限元离散模型如图2所示。静荷载作用包括分缝自重、温降荷载和水荷载,其中,为了检验本文横缝模型对初始抗拉强度和键槽影响的模拟,采用较低的水位,假设自由表面距坝底为100m,这样温降荷载可以在横缝间产生一定的拉应力。
图1 拱坝横缝布置图Fig. 1 The layout of arch dam contraction joint

图2 拱坝坝体有限元离散Fig. 2 The finite element discretization of arch dam
混凝土材料的弹性模量2.1×1010Pa,质量2400kg/m3,泊松比0.17,热膨胀系数1×10-5,横缝之间的摩擦系数取为1.0。假定缝面为平面,键槽高度HShrKey为10cm,混凝土的抗剪强度fs取为2×106Pa,横缝的初始抗拉强度ft取为0.5×106Pa。分别针对三种横缝模型进行计算:①模型1:横缝无初始抗拉强度,键槽在横缝张开后对切向运动无约束;②模型2:考虑横缝初始抗拉强度和键槽抗剪能力随横缝张开度变化,即本文提出的修正横缝模型;③模型3:整体坝模型,即假设横缝的初始抗拉强度和键槽抗剪强度无限大。
图3~图8分别为采用3种不同横缝模型所得到的拱坝上、下游坝面最大主应力、最小主应力的分布图。3种不同横缝模型的最大主应力和最小主应力见表1。
图9和图10分别为采用横缝模型1、2所得到的拱坝上、下游坝面横缝开度分布图。
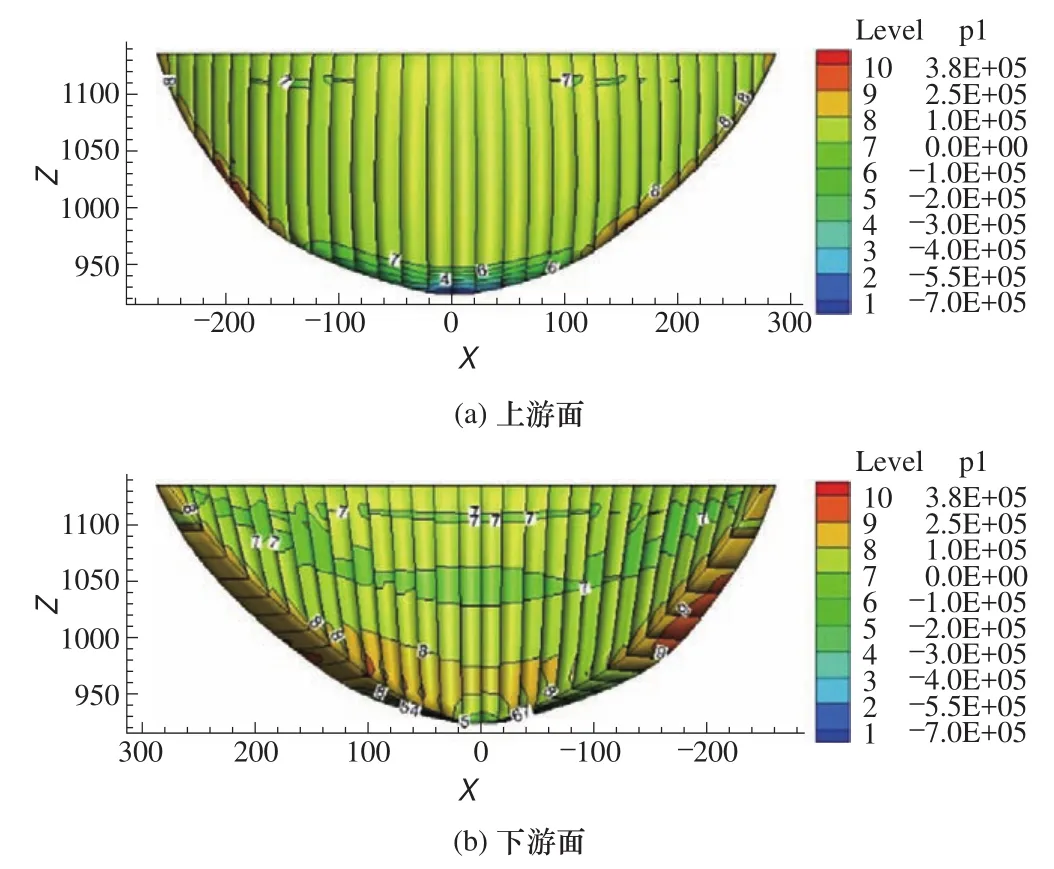
图3 横缝模型1的拱坝上、下游面最大主应力分布图Fig. 3 The arch dam upstream and downstream surface maximum principal stress distribution of contraction joint model 1
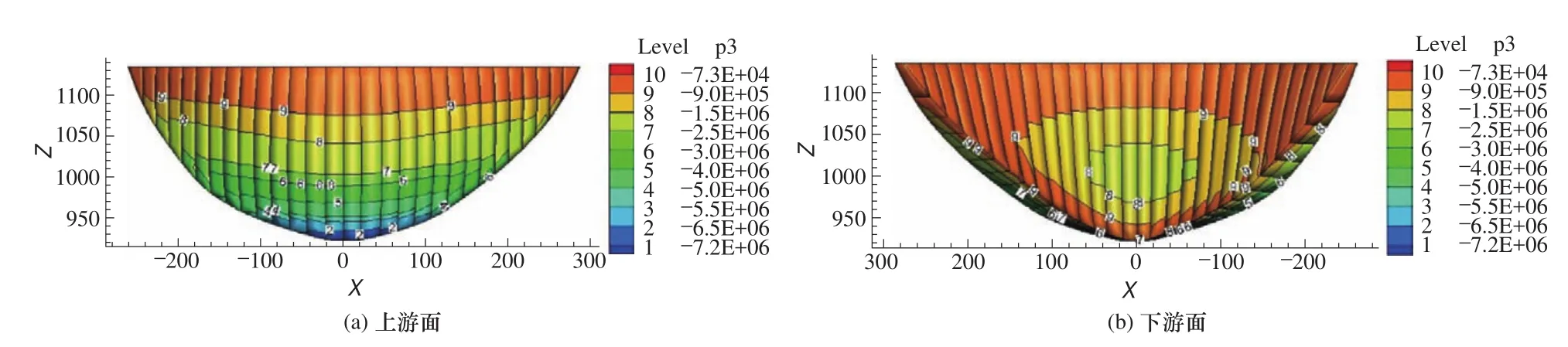
图4 横缝模型1的拱坝上、下游面最小主应力分布图Fig. 4 The arch dam upstream and downstream surface minimum principal stress distribution of contraction joint model 1
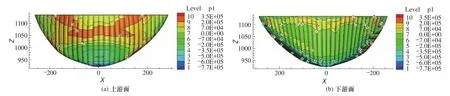
图5 横缝模型2的拱坝上、下游面最大主应力分布图Fig. 5 The arch dam upstream and downstream surface maximum principal stress distribution of contraction joint model 2
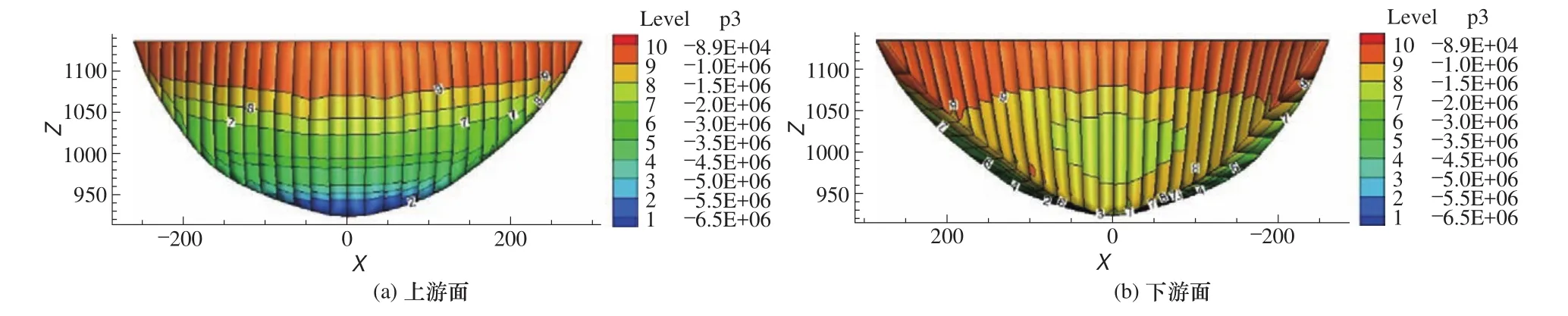
图6 横缝模型2的拱坝上、下游面最小主应力分布图Fig. 6 The arch dam upstream and downstream surface minimum principal stress distribution of contraction joint model 2

图7 横缝模型3的拱坝上、下游面最大主应力分布图Fig. 7 The arch dam upstream and downstream surface maximum principal stress distribution of contraction joint model 3

图8 横缝模型3的拱坝上、下游面最小主应力分布图Fig. 8 The arch dam upstream and downstream surface minimum principal stress distribution of contraction joint model 3

表1 3种不同横缝模型的主应力极值Tab.1 The principal stress extremum of 3 contraction joint models
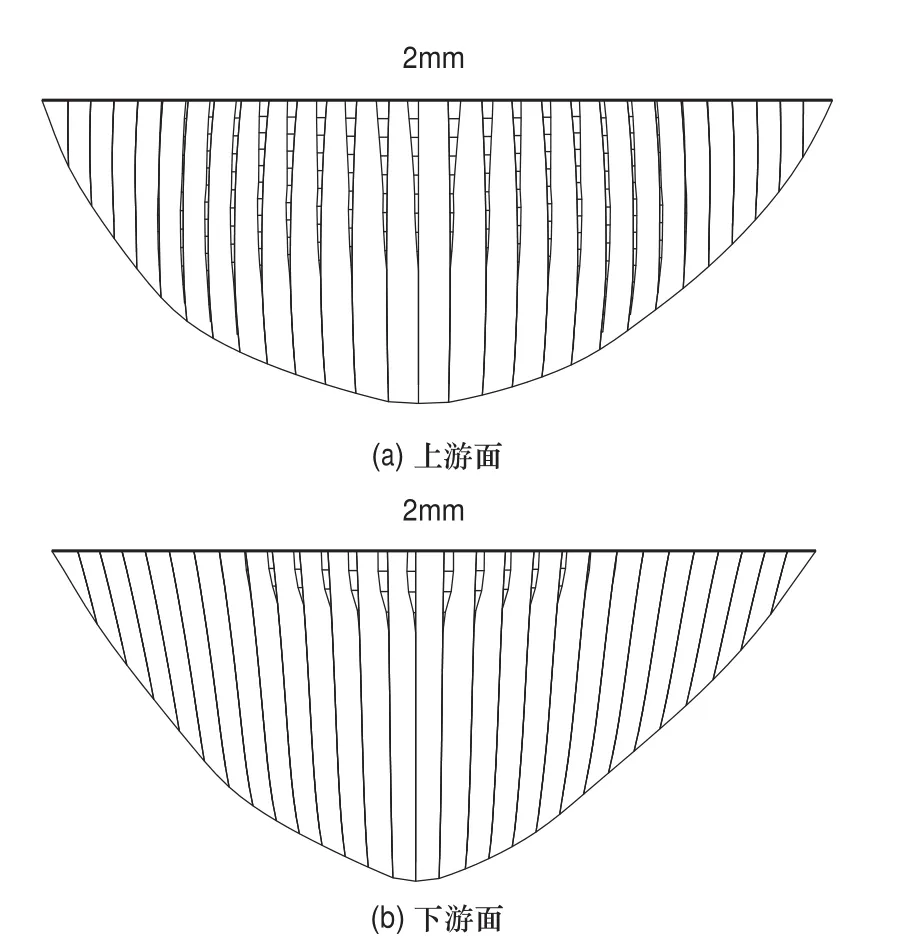
图9 横缝模型1的拱坝上、下游面横缝开度分布图Fig. 9 The arch dam upstream and downstream surface opening width distribution of contraction joint model 1
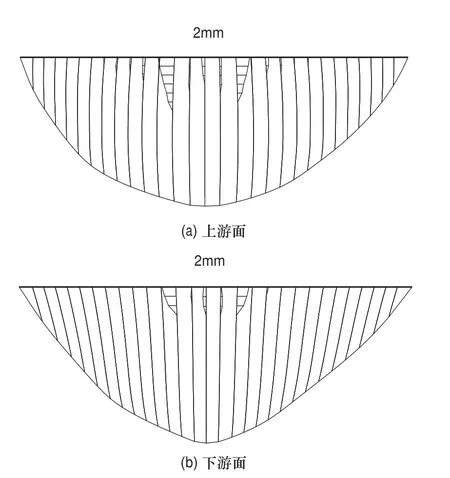
图10 横缝模型2的拱坝上、下游面横缝开度分布图Fig. 10 The arch dam upstream and downstream surface opening width distribution of contraction joint model 2
图11和图12分别为采用横缝模型1、2、3所得到的拱坝上游坝面沿横河向、顺河向的位移分布图。对于竖向位移,不同横缝模型得到的计算结果基本相同。
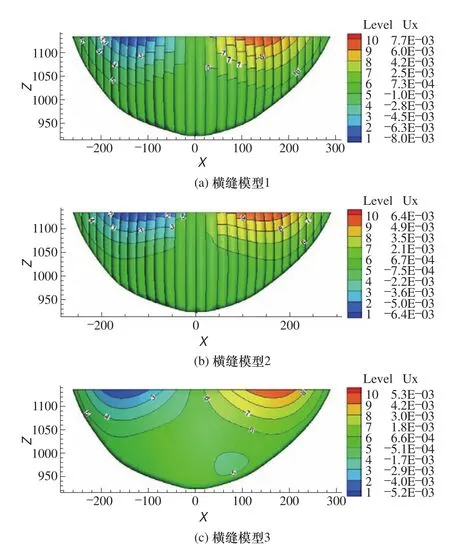
图11 不同横缝模型的拱坝上游面横河向位移分布图Fig. 11 The arch dam upstream surface transverse displacement maps of different contraction joint models
(1)对于模型1,在上游坝面拉应力较小,大部分为0~0.1MPa;对于模型2,上游坝面中上部的局部区域拉应力为0.1~0.3MPa;两种模型的上游面拉应力分布有较大的差别。这是因为:模型1中横缝不承受拉应力,这样对于温降荷载引起的坝体体积收缩而产生的拱向拉应力无法在坝体中上部高程范围内的坝块之间传递;而模型2中,只要横缝拉应力小于灌浆材料的抗拉强度,则拱向拉应力可以在坝块之间进行传递。
(2)对于模型2,坝体顶拱中部拉应力较小,而且从横缝开度图10可见,在顶拱中部横缝张开,说明此处由温降产生的拱向拉应力较大,超过横缝灌浆材料的抗拉强度,但在坝体中、下部,应力大小和数值基本相同,说明在这些位置,横缝未张开。
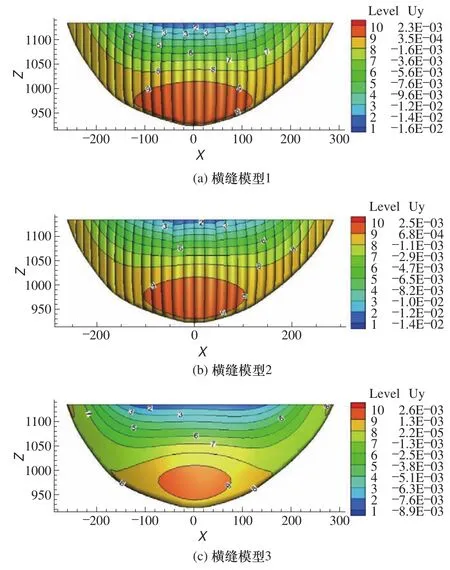
图12 不同横缝模型的拱坝上游面顺河向位移分布图Fig. 12 The arch dam upstream surface along river displacement maps of different contraction joint models
(3)对于压应力,在下游坝面,三种模型得到的上、下游坝面应力分布基本相似,其中,模型2、3得到的数值基本相同,模型1的应力在坝踵处略大,其余部位与模型2、3基本相同。这说明压应力的大小和分布主要以水荷载作用为主。
由表1可知:模型2的最大主应力小于模型1和模型3;模型2的最小主应力与模型3的最小主应力相等,比模型1的小。说明不同的横缝模型对温降荷载作用下坝体主应力数值大小有较大的影响。
由坝面横缝开度分布图9和图10可见:
当采用模型1时,左、右1/4拱之间的坝块的中上部高程横缝张开度较大;采用模型2时,相比于模型1,横缝张开的范围减小,仅拱冠及其附近坝块的横缝上部高程发生张开现象,且横缝最大张开度超过模型1的最大张开度将近2~3倍,这与横缝张开时,键槽仍保持较大的切向约束能力有关。
由上游坝面横河向、顺河向位移分布图11和图12可见:
(1)沿横河向,三种横缝模型得到的位移分布基本相同,在坝体下部,位移的数值基本一致;模型1的位移值最大,且在横缝处,特别是坝顶部,位移分布呈现较为明显的不连续性,坝体中上部横缝张开范围较大;模型3的位移最小;模型2的位移分布在拱冠及其附近横缝的顶部出现较为明显的不连续性,在其余的横缝处,位移场基本连续。
(2)沿顺河向,三种缝模型得到的位移分布基本相同,特别是坝体中下部、坝踵处的位移值相差不大;在中上部坝面,模型1、2得到的位移值相差不大,并略高于模型3的位移值。当横缝闭合时,模型1、2的切向约束都比较强;当横缝张开时,通过对计算结果的检验,发现模型1出现切向滑动,错动量的量级为1e-2mm,与相应部位的顺河向位移相比,数值相对较小,而模型2中,由于横缝开度较小,则键槽仍保持较强的切向约束作用,使得切向滑动几乎为0。因此,模型1、2沿顺河向的位移相差不大。
3 结束语
本文提出了一种可以考虑法向初始抗拉强度、切向抗剪强度变化的横缝接触模型,用于模拟拱坝横缝灌浆后所具有的初始抗拉强度、键槽抗剪能力随横缝开度变化的变形特点。数值试验表明,在低水位条件下,不同的横缝模型对温降荷载作用下坝体上游面中上部高程的拉应力分布和数值大小有较大的影响。一方面,当水位较低、坝体上部的拱向压力较小,温降荷载可能会引起拱向拉应力,本文提出的模型可以通过考虑法向初始抗拉强度,使得这种拉应力可通过横缝在相邻坝块中进行传递。另一方面,由于键槽切向约束与张开度相关,因此,当横缝张开时,仍能提供一定的切向约束。因此,本文提出的横缝计算模型将有助于更合理地模拟静荷载作用下拱坝横缝的工作形态。但对于模型中的切向抗剪强度、横缝内砂浆抗拉强度等参数还需要与实际工程条件相符合;另外,本文中的平缝假设与实际键槽具有较为复杂的几何形状不相符,还需对相应的摩擦系数、键槽抗剪强度等等效参数的确定做进一步的研究。
[1] 林继镛. 水工建筑物[M]. 第5版. 北京: 中国水利水电出版社,2009.
[2] Niwa A,Clough W R. Non-linear seismic response of arch dams[J]. Earthquake Engineering and Structural Dynamics,1982(10):267-281.
[3] 徐艳杰,张楚汉,王光纶,等. 小湾拱坝模拟实际横缝间距的非线性地震反应分析[J]. 水利学报,2001,(04):68-74.XU Yanjie,ZHANG Chuhan,WANG Guanglun,et al. Nonlinear Seismic Response Analysis of Arch Dam with Contraction Joints[J]. Journal of Hydraulic Engineering,2001,(04):68-74.
[4] Dowling M L,Hall J F. Nonlinear Seismic Analysis of Arch Dams[J]. Journal of Engineering Mechanics,1989,115(4):768-789.
[5] Fenves G L,Mojtahedi S,Reimer R B. ADAP-88: A Computer Program for Nonlinear Earthquake Analysis of Concrete Arch Dams[R]. Report No. UCB/EERC-89/12,1989.
[6] 杜修力,涂劲,陈厚群. 有缝拱坝-地基系统非线性地震波动反应分析方法[J]. 地震工程与工程振动,2000,20(1):11-20.DU Xiuli,TU Jin,CHEN Houqun. Nonlinear Seismic Response Anslysis of Arch Dam-foundation Systems with Cracked Surfaces[J]. Earthquake Engineering and Engineering Vibration,2000,20(1):11-20.
[7] 林皋,胡志强. 拱坝横缝影响及有效抗震措施的研究[J]. 世界地震工程,2004,(03):1-8.LIN Gao,HU Zhiqiang. Studies of the effect of contracion joints and the effective earthquake-resistant measures for arch dams[J].World Earthquake Engineering,2004,(03):1-8.
[8] 赵兰浩. 考虑坝体—库水—地基相互作用的有横缝拱坝地震响应分析[D]. 河海大学,2006.
[9] LIU J B,WANG D,YAO L. Contact Force Model in the Dynamic Analysis of Contactable Cracks[J]. Acta Mechanica Solida Sinica,1993,6(4):439-452.
[10] 胡志强. 考虑坝—基动力相互作用的有横缝拱坝地震响应分析[D]. 大连理工大学,2004.
[11] 赵兰浩,李同春,牛志伟. 有横缝高拱坝非线性地震响应动接触模型[J]. 水力发电学报,2007,(04):91-95.ZHAO Lanhao,LI Tongchun,NIU Zhiwei. The Dynamic Contact Model of Nonlinear Seismic Response of High Arch Dams with Contraction Joints[J]. Journal of Hydroelectric Engineering,2007,(04):91-95.
[12] Christensen P W,Klarbring A,Pang J S,et al. Formulation and Comparison of Algorithms for Frictional Contact Problems[J]. Int.J. Num. Meth. Engrg,1998,42:145-173.
[13] Pang J S. Newton’s method for B-differentiable equations[J].Mathematics of Operations Research. 1990,15:311-341.
2017-03-23
2017-05-19
牛智勇(1994—),男,硕士研究生,主要从事拱坝结构分析。E-mial: nzyee@mail.dlut.edu.cn
胡志强(1972—),男,副教授,博士,主要从事混凝土坝-库水-地基系统抗震分析方法研究。E-mail: huzhq@dlut.edu.cn
林 皋(1929—),男,教授,中国科学院院士,主要从事大坝、核电结构抗震理论和模型试验技术研究。E-mail: gaolin@dlut.edu.cn
A study on contraction joint model with normal initial tensile strength and variable tangential shear strength for arch dam
NIU Zhiyong,HU Zhiqiang,LIN Gao
(Faculty of Infrastructure Engineering,Dalian University of Technology,Dalian 116024,China)
The integrity of arch dam can be obtained after the contraction joints are grouted. The mortar in the joints is able to bear the tensile stresses below the tensile strength. Moreover,the constraints of sphere or trapezoidal shear keys in tangential direction will vary with the opening of the joints. In this paper,based on the contact model represented by the B-differential Equations,an updated model is proposed in which the initial tensile strength and relationship between shear strength of shear key and joint opening is taken into consideration. Numerical example shows that the tensile stresses can be transferred between adjacent dam monoliths through joints,and the shear keys can provide large tangential constraints even if the joints open.
arch dam;contraction joint;initial tensile strength;shear keys
TV311
A学科代码:570.25
10.3969/j.issn.2096-093X.2017.03.014
十三五国家重点研发计划“复杂工程力学高性能应用软件系统研制”(2016YFB0201000)

