基于空间滞后模型的出租车需求影响因素分析

张自荷 王 振 吴 瑞

(长安大学公路学院1) 西安 710064) (北京交通发展研究院2) 北京 100161)

0 引 言

出租车是城市公共交通系统的重要组成部分[1].现阶段，出租车行业在空间区域面临需求与供给不匹配的问题[2]，因此，对不同城市区域的出租车需求量进行精准预测对提高出租车服务水具有十分重要的意义.需求量预测的常用方法有原单位法、增长率法、聚类分析法、函数法和回归分析法.当自变量和因变量等相关数据可以准确获取时，回归分析可以很好得对未来出行量进行预测[3].出租车GPS数据作为地理空间活动记录数据，包含了车辆的设备状况、运营状态、地理位置信息、瞬时速度以及运行方位角等信息[4]，现已被用来进行交通状态的估计[5]、交通行为分析[6]、出行OD预测[7]和出行时间预测[8]，但目前较少研究关注利用出租车GPS数据研究高峰时期的出租车需求，且建模过程中未考虑需求在空间上的依赖关系和聚集现象.

综上，文中基于出租车GPS数据，通过提取上车点获得基于交通小区的出租车需求，构建空间回归模型，研究高峰时期出租车需求的影响因素并对结果进行讨论，为城市公共交通系统优化、高峰时期出租车需求量预测等提供方法支撑和研究途径.

1 数据预处理

1.1 GPS数据预准备

出租车GPS数据由车载终端生成，通常为每隔15～60 s采集一次数据信息并采用及时通信方式上传至数据中心的数据库中.本文所采用数据为西安市2017年4月17日绕城高速范围内的出租车GPS数据，所选日为星期一，天气晴朗，无重大节假日，因而保证了数据所具有的代表性.数据包含信息中与本研究相关的包括车牌号、经度、纬度、GPS时间、车辆载客状态，其形式见表1.

表1 与本研究相关的出租车GPS数据结构

出租车交通行为由多个在时空上连续的GPS轨迹点组成，构成车辆的行驶轨迹，并可反应车辆上、下客活动信息[9].本文研究的是出租车需求的影响因素，因此，首先需要从一系列轨迹点中提取上车点的经纬度信息以确定出租车上客点在空间上的数量与分布.以西安市出租车GPS为例，具体提取步骤如下：①数据清洗，删除状态位无效，存在数据错误或缺失，车辆状态值为0，1，2，3，6，7的记录；②数据排序，按车牌号聚类并按时间升序排列；③上下车点提取，将车牌号相同的由持续的车辆状态值为4转变到状态值为5和紧邻的持续状态值为5转变到状态值为4的两点提取出来，将此两点认为是一次完整出行的上、下客点.

通过上述提取步骤，获得绕城高速区域内11 634辆营运出租车的356 972条行程数据，其全天上客点随时间的分布见图1，其中早、晚高峰时段(参照相关研究，本文早高峰时段确定为07：00—09：00，晚高峰确定为18：00—20：00出行量分别为32 420次和35 162次，占比为9.1%和9.9%，全天平均小时出行量为14 874次.考虑现有研究未涉及到高峰时段出租车出行量影响因素且晚高峰出行量较高，故选择晚高峰时段作为研究对象.

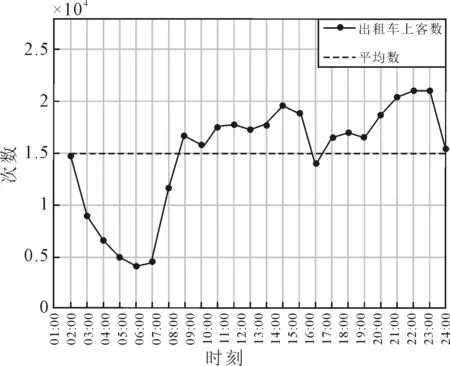
图1 绕城高速范围内出租车出行量的时间分布

1.2 地图匹配

地图匹配是指在ArcGIS软件中通过一致坐标系下的空间位置关系将出租车上客点连接至路网线地理文件和交通小区面地理文件，其中，交通小区是用来预测出行产生和吸引的最基本的分析单元，通常包含人口数量、工作岗位数量、机动车拥有量等属性信息，本研究中将西安市绕城高速范围内区域划分为601个交通小区，每个小区内包含2011年西安市综合交通调查获取的常驻人口、宾馆流动人口、岗位数、小汽车拥有量等属性数据.通过统计晚高峰时段落在各交通小区内部的上客点数量获得各小区的晚高峰出租车需求[10]，见图2.

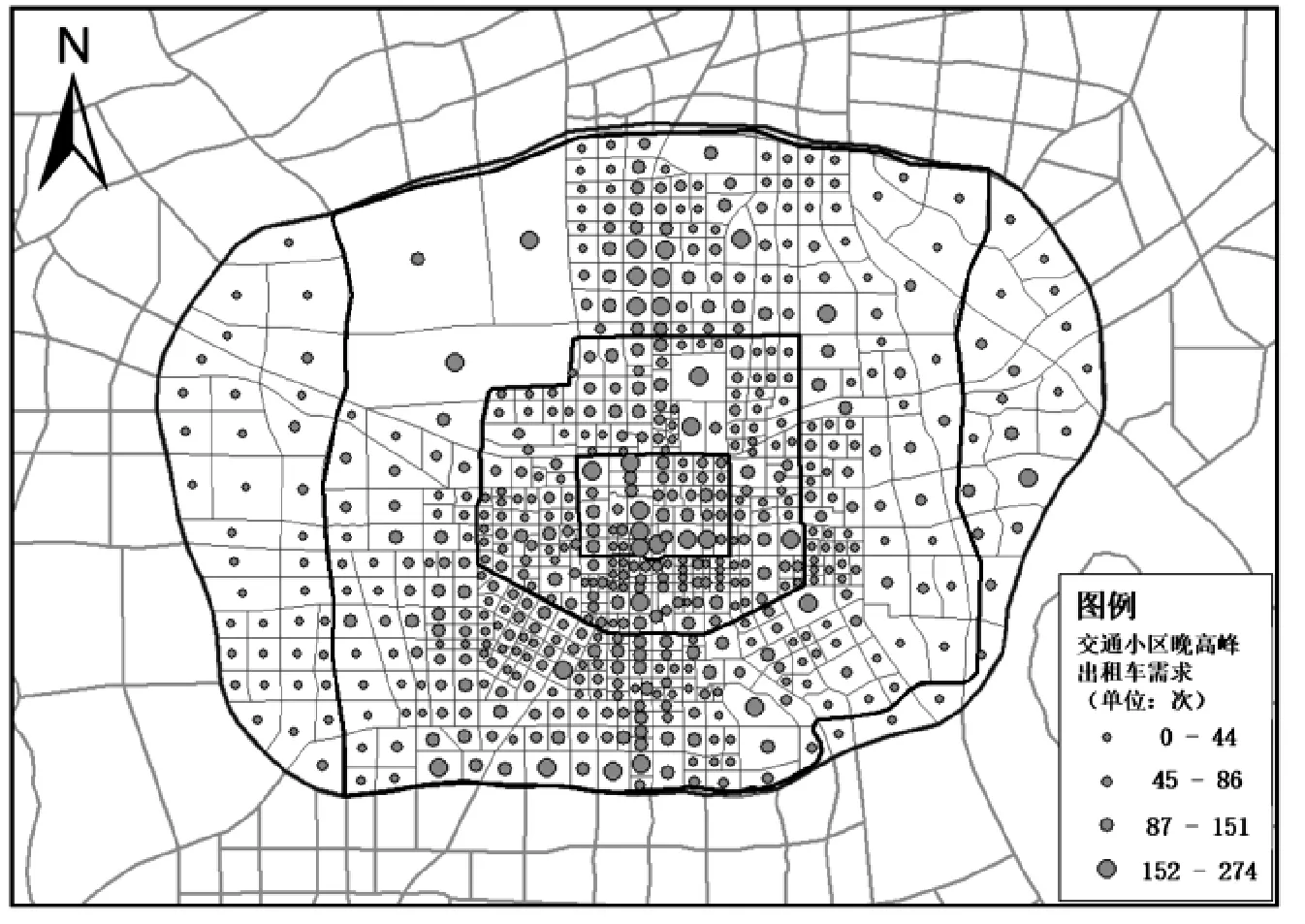
图2 交通小区晚高峰出租车需求空间分布

2 出租车需求影响因素分析

2.1 出租车需求相关影响因素分析

出租车需求预测可分为短期预测和中长期预测[11].中长期预测用于出租车宏观管理和规划，短期预测为出租车实时调度提供依据，本文主要研究的是出租车中长期出行预测.综合已有文献，影响出租车中长期需求的影响因素包括，总人口数量、就业人口数量、小汽车拥有量、性别占比等区域人口属性；通勤出行时间、出行目的等出行特征[12]；商业区面积、居住区面积等土地利用特征[13]；停车场供给，公共车供给，地铁供给，自行车道密度等其他交通方式供给特征等因素.

2.2 地铁可达性指标构建

公交车供给和地铁供给这两个影响因素，通常通过可达性进行量化，即对于某个目的点来讲，乘坐公交车的便利程度.可达性由可达性指标表征，通常与到达该点车辆频次、车站距离目的地的步行时间等影响因子有关，然而，由于很难获得整个城市的具体公交车频次信息，现有研究多只计算特定区域内公交可达性指标.考虑到数据可得性，本文仅计算各交通小区的地铁可达性指标(metro access time, MAT)，借鉴文献[3]对公交可达性指标的定义方法，本文将其定义为每个交通小区的质心到距离最近地铁站的步行时间加上地铁等待时间，其中，步行速度取4 km/h，等待时间按发车间隔时间的1/2计算，为

(1)

式中：f为每小时的地铁发车频次；D为基于拓扑路网的交通小区质心到最近地铁站的步行距离；Vw为步行速度.地铁可达性越高，地铁可达性指标(MAT)越小.

2.3 数据准备与变量定义

选用的潜在自变量及变量解释见表2.受城市布局和功能结构影响，出租车需求在某些交通小区较高，而在某些交通小区较低，因此，研究区域内基于交通小区的晚高峰出租车需求直方图呈现偏态分布，见图3.为满足后续建立线性回归模型的因变量正态分布假设前提，将因变量进行对数转换，结果见图4.为保持与因变量的一致性以更好表征两者间的线性关系，各潜在自变量也做相应对数变换.

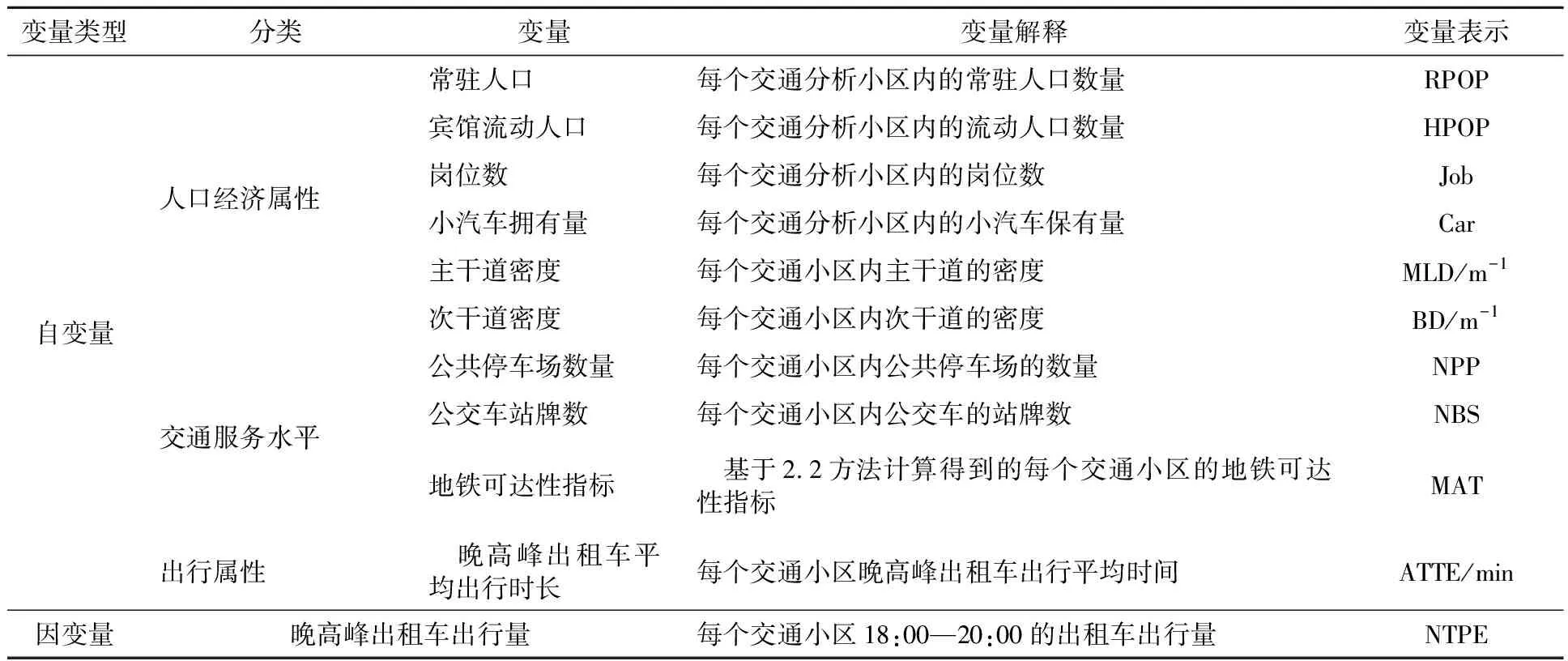
表2 潜在自变量和潜在因变量的定义

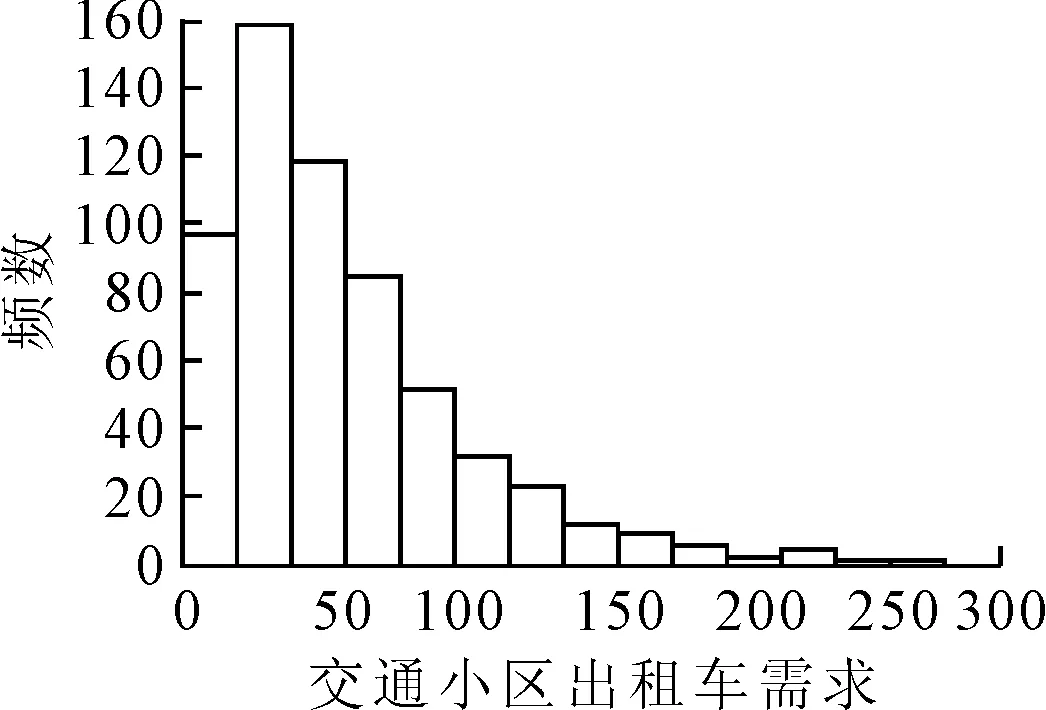
图3 晚高峰出租车需求直方图

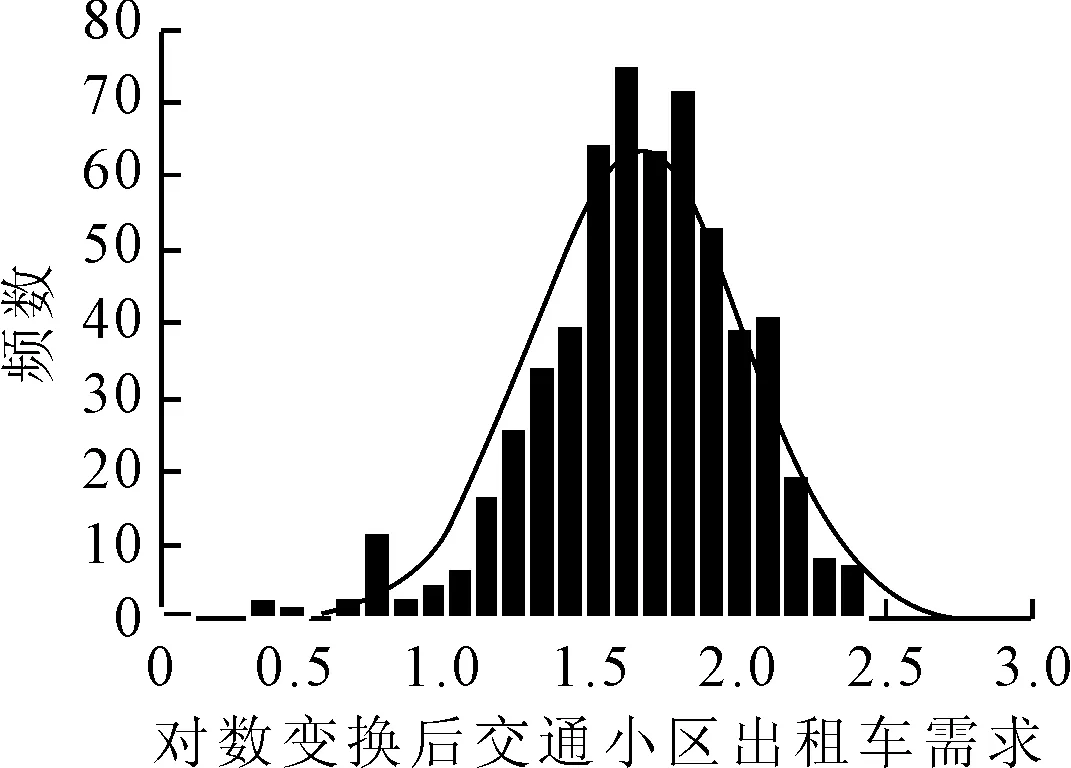
图4 对数变换后晚高峰出租车需求直方图

3 考虑空间自相关的出租车影响因素建模

3.1 全局空间自相关

通过晚高峰出租车上车点可视化结果，可以看出某交通小区晚高峰出租车需求与邻近交通小区晚高峰出租车需求相关，即以交通小区为单位的出租车需求具有空间相关性，若基于统计学和传统计量经济学理论对此类存在空间相关性的样本进行建模，将会导致较大的方差估计、较低的假设检验显著水平和较低的拟合度，因此，需要对此类数据进行空间相关性检验.通过构建全局Moran’s I指标检验出租车需求在统计学上是否具有空间集聚特征，计算式为

(2)

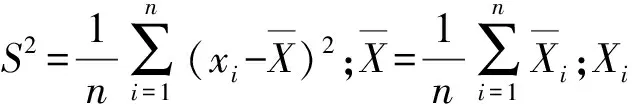
(3)

根据各交通小区的空间关系构建空间权重矩阵，利用Geoda软件计算得到晚高峰各交通小区出租车需求的全局Moran’sI指数为0.440，检验的Z值为20.025，表明在1%的显著水平上通过了检验，即晚高峰期间出租车需求在空间上是正相关的.

3.2 空间滞后模型建立

由于晚高峰出租车需求在研究区域是空间正相关的，因此对其建模时，应充分考虑因变量在空间上不独立这一前提，将地区间的相互关系引入模型，采用基于空间权重矩阵对传统线性线性回归模型进行改进的空间计量模型进行模型构建.空间计量经济模型根据经济活动的空间相依性和回归模型中的误差项的相依性特征基本分为两类模型：空间滞后模型和空间误差模型，而这两类模型的构建的都是以相应的线性回归模型为基础的，因此，本文首先对各影响因素变量与因变量之间的相关性和各影响因素之间的相关性进行检验，筛选出进入回归模型的潜在自变量.其次，建立普通线性回归模型并构建判别指标选出适合的空间计量模型.最后，建立空间计量模型，利用最大似然法对系数进行估计，将回归结果与普通最小二乘法的回归结果进行比较，分析变量的系数变化及拟合度差异.

3.2.1潜在自变量的筛选

由于潜在自变量较多，为避免无效变量进入模型，先对各潜在自变量进行初步筛选，从而选出进入回归模型的自变量.考虑到本研究中各自变量均为数值型变量，采用皮尔逊相关系数矩阵计算出各潜在自变量与因变量之间的相关系数，通常，统计显著情况下相关系数绝对值大于0.5被作为潜在自变量进入模型的依据，为避免遗漏晚高峰出租车需求的有效影响因素，本文采用在0.01显著水平下相关系数的绝对值为0.2作为潜在自变量进入模型的临界值.为避免自变量之间的共线性导致的回归模型系数有偏估计，本文在上步筛选基础上计算了拟进入模型变量两两之间的相关性系数，相关性系数大于0.7的变量中至多有一个能进入模型.

根据上述原则构建皮尔逊相关系数矩阵对潜在自变量进行筛选，结果表明，宾馆流动人口、公共停车场数量、公交车站牌数和地铁可达性与因变量在0.01显著性水平下的相关性系数分别为0.204，-0.239，0.525和0.219，且四个潜在变量两两之间的相关系数均小于0.7，因此，选择以上四个变量作为进入普通线性回归模型的变量.

3.2.2空间计量模型的建立

1) 普通线性回归模型的建立 空间计量模型是以普通线性回归模型为基础建立的，因此，首先构建如下普通线性回归模型：

(4)

式中：Yi为各交通小区中晚高峰出租车需求；Xi为第i个解释变量；n为自变量的个数，在初始模型中n= 4；a0为模型的截距；ai为对应与Xi的系数.采用最小二乘法对变量系数进行估计，即当观测变量与预测变量间的残差平方和最小时，所得系数为系数估计值.此外，为获得解释度更高的模型，采用逐步回归的方法对初步筛选出的变量进行二次筛选，其优点在于每向模型中引入一个变量，均要考察原来在模型中的自变量是否统计显著，若否，则将变量剔除.

模型的回归结果见表3，模型的拟合优度为0.468，且各变量在0.001的统计水平下显著.变量公共停车场数量和变量公交车站牌数的系数分别为0.544和0.219，表明这两个变量对出租车需求的影响均为正向的.变量地铁可达性指标的系数为-0.218，结合前述地铁可达性指标算法可知，该指标越小，地铁可达性越高，因此，地铁可达性越高的地方相应的出租车需求也越高.从模型的总体结果来看，与停车场、地铁和公交车服务供给越多的地方，出租车需求越少的预期相反，其他机动车方式越便捷的区域，出租车需求也相应越高，这可能与两个原因相关：①公共停车场、地铁和公交车服务供给较多的区域，通常出行需求也较旺盛；②出租车因其灵活的出行方式，可作为其他交通方式的接驳以完成基于“门到门”的出行过程.

由于各交通小区的出租车需求为空间变量，为检验普通线性回归模型的残差中是否存在未解释成分，对其残差进行空间自相关检验，结果表明，Moran’sI统计值为0.360，相应的Z得分为16.354，即在0.01显著性水平下，拒绝残差不具有空间自相关性的原假设.这说明普通线性回归模型对因变量的未解释部分是未考虑因变量之间的空间相对关系造成的，因此，需要建立空间模型来解释出租车晚高峰需求.

2) 空间模型选择 空间滞后模型和空间误差模型作为两种基础的空间计量模型，充分考虑了变量之间的空间交互效应，其区别体现在空间滞后因子的构成上.在空间滞后模型(spatial lag model，SLM)中，空间滞后项由空间权重矩阵与因变量乘积构成，作为模型右侧的解释变量之一；

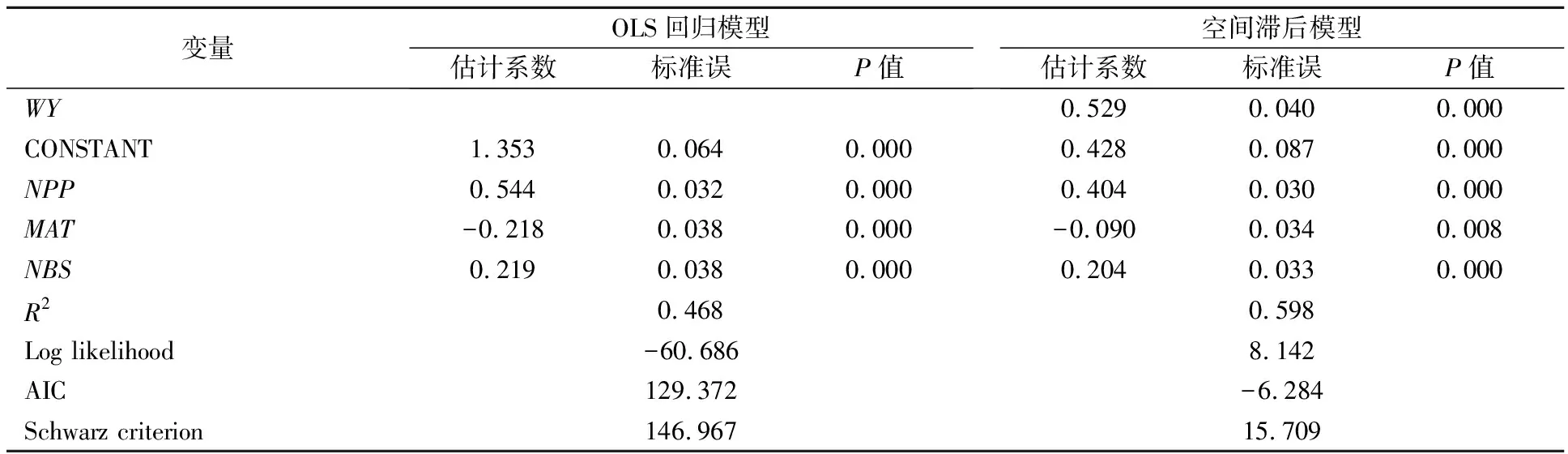
表3 模型估计结果

在空间误差模型(spatial error model，SEM)中，空间滞后项由空间权重矩阵与误差项乘积构成，作为误差项的解释变量，但不作为因变量的解释变量.构建两个拉格朗日乘数(Lagrange multiplier)形式LMERR、LMLAG及其稳健的R-LMERR、R-LMLAG来实现空间滞后模型与空间误差模型的选择，Anselin 等[14]给出的判别准则：若在空间效应的检验中发现当LMLAG较之LMERR在统计上更加显著，则选择空间滞后模型较为合适；相反，若LMREE比LMLAG在统计上更加显著，且R-LMERR显著而R-LMLAG不显著，则选择空间误差模型较为合适.表4为基于普通线性回归模型的空间效应检验结果，由两类拉格朗日乘数检验可以看出，LMLAG较LMERR在统计上显著，且R-LMLAG在0.01水平下显著而R-LMERR不显著，因此空间滞后模型更适合拟合出租车晚高峰需求.

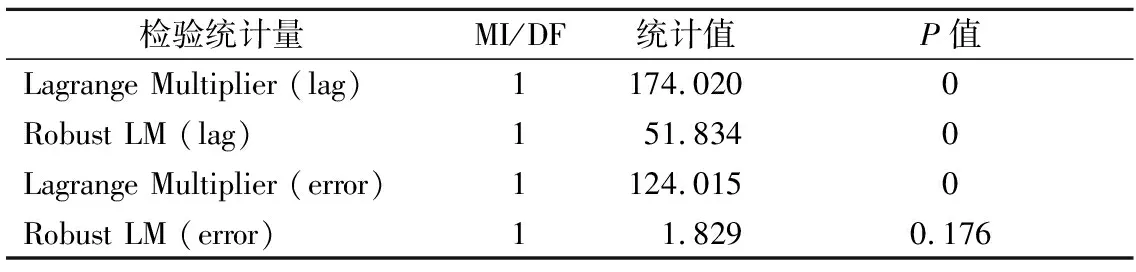
表4 晚高峰出租车需求的空间效应检验

3) 空间模型的建立及分析 针对晚高峰出租车需求的空间滞后模型为

Y=ρWY+Xβ+ε

(5)

式中：Y为N×1维因变量向量；X为包含解释变量公共停车场数量，地铁可达性和公交站点数量的N×3维向量；WY为前述的空间滞后因子；ε为N×1维误差向量；W为N×N维空间权重矩阵，与前述空间自相关时建立的权重矩阵相同，β为解释变量的系数；ρ为空间自相关系数；N=601为研究区域内交通小区的数量.假设误差服从均值为零，方差为σ2的独立同分布，且与解释变量X不相关，即E(X′ε)=0.当空间自相关效应存在时，空间滞后项的系数ρ≠0, 即出现变量的内生性问题，普通最小二乘估计将不再适用,因此本文采用最大似然估计法(ML)对各自变量的系数进行估计.

利用Geoda软件得到的空间滞后模型的估计结果见表3.由表3可知，模型的拟合优度指标R2由0.468提高到0.598，对数似然值Log likelihood有所增大，同时，从赤池信息准则和施瓦茨准则看，模型的AIC值和SC值都有所下降，且空间滞后项 的系数在0.01水平下显著，因此，空间滞后模型的整体拟合效果较好.从模型的系数估计结果看，所有系数均在0.01水平下显著，空间滞后项的系数为0.529，表征当某个小区的出租车需求较高时将会对与它有共同边或节点的临近交通小区的出租车需求产生正向的影响，即出租车需求具有区域溢出效应.此外，引入空间滞后项后，各变量的系数虽符号未变，但其绝对值都较未引入前有所减少，表明晚高峰某交通小区的出租车需求不仅与这一交通小区内的公共停车场数量、地铁可达性和公交车站牌数均成正向关系，也与周边交通小区的出租车需求有很大的正向关系.

4 结 论

1) 在对出租车GPS轨迹数据进行预处理的前提下，提取上客点的地理位置，通过统计落在各交通小区的上客点数量，得到了各交通小区晚高峰时段的出租车需求.

2) 晚高峰出租车需求的全局空间自相关检验结果表明，晚高峰期间出租车需求在空间上是正相关的，因此将其作为因变量进行建模时应充分考虑其在空间上不独立这一特征.

3) 空间滞后模型的估计结果表明，空间滞后项在0.01统计水平下显著，且其整体拟合效果优于普通线性模型，因此，空间滞后模型能更好的对晚高峰出租车需求进行拟合.

4) 晚高峰出租车需求与地铁可达性、公共汽车站数量、公共停车场数量均成正相关，且考虑空间因素后，这些变量对出租车晚高峰需求的影响有所降低.