运载火箭自适应减载控制技术

潘 豪，冯 昊，李新明，胡煜荣，王光辉

（1.北京航天自动控制研究所，北京，100854；2.宇航智能控制技术国家级重点实验室，北京，100854）

0 引言

随着运载火箭轻质化发展，新型中型运载火箭对箭体结构的气动承载能力提出更高的要求，需要将气动载荷在飞行过程中控制在一定的范围。根据对运载火箭飞行气动环境的认识程度，基于发射前可确定的高概率平稳风，调整飞行姿态，减小飞经大风区时的合成攻角从而降低气动载荷，是一种前馈补偿的控制方式；对由于风场梯度变化带来的不确定切变风以及随机风干扰，需通过直接或间接在线辨识气动攻角方式，以自适应控制方式进行实时主动减载。

为提高减载效果和适应性，新型运载火箭采用了主动减载的控制方式。国外的大型运载火箭多数采用主动载荷控制，用于减小大风区飞行时的合成攻角以减小气动载荷。美国重型运载火箭SLS在自适应增广控制模块中包含了减载控制设计[1]；法国的阿里安火箭在姿控设计时增加了减载控制回路，开展了主动减载控制设计[2]。在中国，倪少波[3]等提出了一种大气层内无动力低速飞行器过载反馈控制方法，解决了弹上计算出来的攻角不能反应真实攻角等问题；杨伟奇[4]、宋征宇[5]等采用自抗扰控制器进行风载干扰抑制，通过数学仿真验证表明具有一定的减载效果。

新型中型运载火箭一级基本在稠密大气层内飞行，由于攻角、侧滑角和风的存在，始终有气动力和力矩作用在火箭箭体上，气动力的存在会干扰到箭体质心横、法向运动，使质心运动偏离了标准弹道，气动干扰力矩的存在会使箭体产生绕心运动，即带来姿态偏差。在火箭箭体结构强度足够大、控制力矩足够大的情况下，传统的姿控系统设计可以保证火箭的姿态稳定。但对新型运载火箭而言，在进行总体结构设计时为了提高运载能力会尽量减小结构质量，因此箭体结构承受气动载荷与控制力矩相互作用而形成的弯矩的能力严重下降，通过在线主动控制，减小攻角、侧滑角可以有效的减小作用在弹体上的气动载荷，从而达到卸载的目的，而当火箭飞出稠密大气层后，气动力矩的用会迅速下降，无需再进行载荷控制。

本文结合新型中型运载火箭研制采用的主动减载控制设计，研究分析基于横法向过载传感器和扩张状态观测器的自适应减载控制方法，分析各自的减载控制特点。

1 基于过载传感器的主动减载控制

1.1 运载火箭飞行动力学模型

考虑运载火箭弹性运动和液体晃动影响，为便于减载设计分析，以纵向运动为例，基于冻结系数法和小扰动线性化的假设建立小偏差方程。

简化后描述质心运动的小偏差动力学方程为

式中 ∆θ为弹道倾角偏差；∆ϕ为俯仰角偏差；∆α为攻角偏差；为俯仰控制摆角和角加速度；αw为风攻角；qi为第i阶弹性广义位移；为第p阶晃动加速度；为干扰力。

描述绕心运动的小偏差动力学方程为

描述弹性运动的方程为

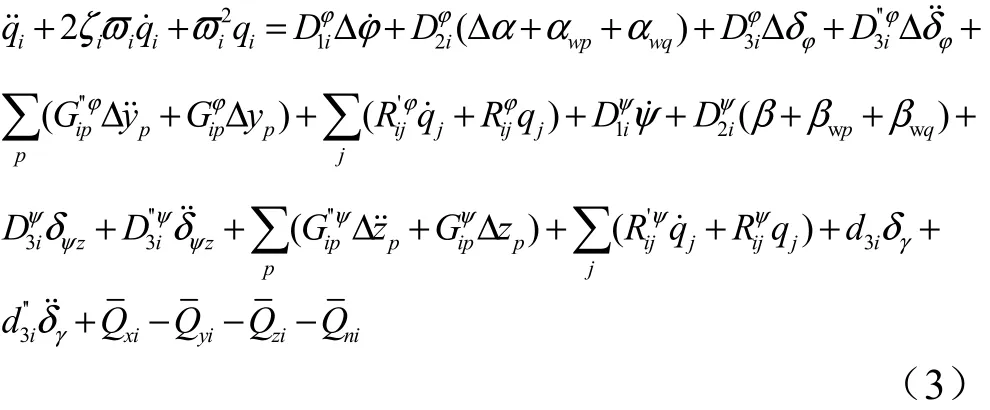
弹性方程为按有限元法进行的弹性振动建模[6]，为偏航控制摆角和角加速度； ∆ δγ, ∆δ˙˙γ为滚动控制摆角和角加速度；均为广义干扰。

式中 ∆yp为第p阶晃动位移；γ˙˙为滚动角加速度。

过载传感器测量的是箭体坐标系下的横法向加速度，其所测量的视加速度为式中1y˙˙为通过加速度表敏感的加速度信息，其中包含了气动、发动机摆动、晃动和弹性等引起的加速度。

1.2 过载控制

采用PID控制方式，从减小横向过载的角度考虑，将零定义为期望过载，进而将过载信号引入到控制方程，相应过载控制框图如图1所示。

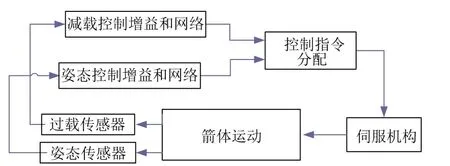
图1 基于加速度表传感器的过载控制框图Fig.1 Load-relief Control Block Diagram based on Acceleration Sensor

通过PID调参，设计合适的控制参数，保证姿态控制闭环稳定同时达到减载目的。下面针对加入过载控制后的动力学控制特点分析。

为便于分析，主要考虑切变风影响，在运载火箭飞行动力学中，忽略高频的弹性运动和晃动运动影响，忽略质心的运动影响，并忽略箭体运动方程和控制方程的动态项，利用简化后的运动方程。

引入过载反馈的控制方程[7]为

可求得响应攻角计算公式：

响应摆角计算公式：

从上面各式可以看出，

a）引入过载反馈后，气动力矩系数 b2变为了对于静不稳定运载火箭，23)0b k> 等效于提高了气动力矩系数，相当于增大了尾翼，可将箭体从静不稳定变成静稳定，从而提高了对气动载荷的飞行适应性；

b）引入过载反馈后，对姿态回路而言控制结构发生了变化，相当于引入干扰，须在姿控系统的稳定性和减载的效果之间进行权衡；

c）过载传感器除敏感箭体的质心运动和绕质心转动产生的视加速度外，还要敏感箭体弹性振动和环境振动产生的加速度，将会对箭体弹性振动产生直接的影响，但抑制弹性将会带来延时，影响减载效果。

2 基于扩张状态观测器的自适应减载控制

2.1 扩张状态观测器与扰动估计

对于二阶被控对象：

式中 M( t)为扰动。

式中0()Mt为未知。对这个系统可建立状态观测器：

将模型中除控制之外的合成项 a( t)看作总扰动，z3( t)就是对该总扰动的估计，可为补偿控制所用。

2.2 运载火箭自抗扰减载控制

考虑火箭俯仰通道绕心运动的状态方程（2），利用扩张状态观测器，令x1=∆ϕ，x2=∆ϕ˙，u=∆δϕ，表示方程中剩余各项，那么，绕心广义力矩 x3包含气动攻角产生的俯仰力矩、角速度产生的阻尼力矩、弹性运动产生的俯仰力矩、晃动运动产生的俯仰力矩、结构干扰等不确定性产生的俯仰力矩。则有如下形式的状态方程：

从而可建立扩张状态观测器方程：

式中01β，02β，03β为可设计的控制器参数。

利用扩张状态观测器估计值，进行反馈补偿，采用如下反馈控制方程：

式中 ()D s为滤波网络，滤除因弹性和晃动运动产生的俯仰力矩；12b zϕ为阻尼力矩。假设扩张状态观测器的估计值准确，则采用该反馈将可以补偿箭体飞行中的风干扰、结构干扰以及不确定性部分，从而可起到减载作用。这样，引入自抗扰反馈后的控制方程为

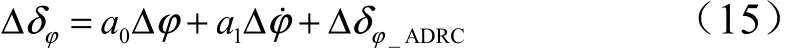
基于扩张状态观测器的减载控制框图如图2所示。

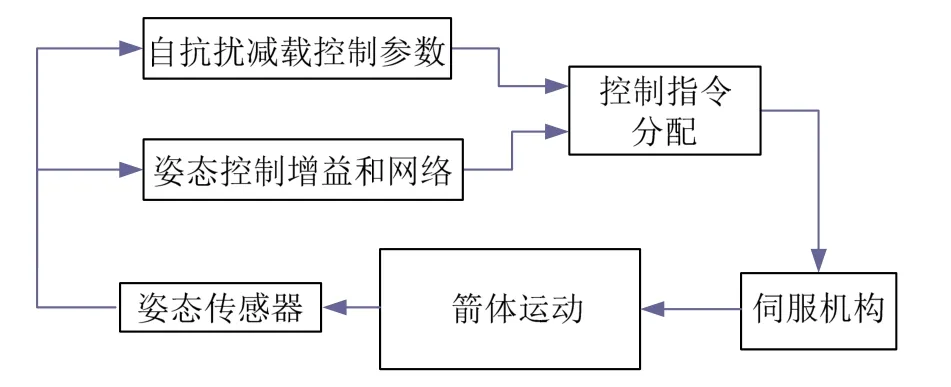
图2 基于扩张状态观测器的减载控制框图Fig.2 Load-relief Control Block Diagram based on ESO

在进行扩张状态观测器设计时，可根据观测器带宽ω大小，选取参数也可以采用相同参数。在观测误差收敛速度能满足要求时的参数也不要取得太大。 β01,β02,β03过大容易使得在初始观测误差较大或者是输出变化太快时使得观测值出现很大的超调。

2.3 运载火箭自抗扰加速度表组合减载控制

考虑用线性组合形式并且引入加速度表反馈设计自抗扰控制器，进行减载控制，控制结构如图3所示。

图3 自抗扰加速度表组合减载控制框图Fig.3 Load-relief Control Block Diagram based on ESO and Acceleration Sensor

引入自抗扰控制和加速度表反馈控制后的控制方程为

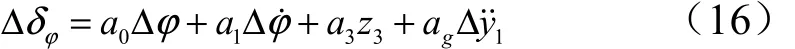
式中 ∆˙y˙1同1.2节，同样忽略高频运动和动态项；z3同2.2节。

3 减载效果仿真分析

以新型中型运载火箭模型为研究对象，针对基于过载传感器的减载控制，基于ESO的减载控制，以及两种方法组合的减载控制，进行正常状态（无偏差组合）的减载效果的仿真，并给出减载效果的比较分析，见图4～6。为对比分析减载效果，在50～110 s内加入若干次三角波切变风干扰。

图4 无减载和基于加速度表的减载对比Fig.4 Comparision of Load-relief Control based on Acceleration Sensor and No Load-relief Control

从图4可以看出，对于基于加速度表的减载控制，与不施加减载相比较，减载效果约为：(3329～2421)/3329=27%。

图5 无减载和基于ESO的减载对比Fig.5 Comparision of Load-relief Control based on ESO and No Load-relief Control

从图5可以看出，对于基于ESO的减载控制，与不施加减载相比较，减载效果约为8%。

图6 两种方法组合与基于加速度表的减载控制对比Fig.6 Comparision of Load-relief Control based on Acceleration Sensor and the Combining Method

从图6可以看出，对于基于两种方法组合的减载控制，与仅用加速度表的减载相比较，减载效果约为2.6%。

4 结 论

本文针对新型中型运载火箭的减载控制问题，以PID控制为基础，从基于加速度表的减载控制和基于ESO的减载控制方法分别进行了分析，经仿真分析，有以下结论：

a） 基于加速度表的过载控制在标称状态下具有较好的减载效果，可满足工程减载研制需求，相比单独使用基于ESO的减载控制效果要好接近20%，具有较大减载优势。

b） 基于ESO的控制虽然提高了抗干扰性能，但较强的滤波特性使得对三角波形式的快变信号反应缓慢，没有起到理想的减载效果。

c）组合形式的减载控制虽对减载效果有一定的提升，但效果不明显，影响了其在运载火箭减载控制上的应用。