运载火箭结构振动疲劳损伤的工程分析方法

薛立鹏，李文斌，司群英，叶 超，孙善秀

（北京宇航系统工程研究所，北京，100076）

0 引言

运载火箭结构在飞行过程中要承受复杂的振动载荷，在研制过程中要进行正弦振动、定频振动及随机振动力学环境考核试验[1,2]，当振动量级较大，结构疲劳强度不足时容易发生疲劳破坏，在新型运载火箭研制的过程中曾发生过结构振动疲劳破坏的现象，振动疲劳的本质是结构所受动态交变载荷（如振动、冲击、噪声载荷等）的频率分布与结构固有频率分布具有交集或相接近，从而使结构产生共振所导致的疲劳破坏现象[3]，对于复杂结构的振动疲劳分析，通常采用有限元方法求得结构的应力响应，然后结合疲劳模型进行结构疲劳损伤的计算和评估。目前对于结构随机振动疲劳损伤的计算研究较多[4～6]，对于结构正弦振动和定频振动研究较少[7]。本文根据Miner线性累计损伤理论结合相应的损伤模型推导了结构的正弦振动、定频振动、随机振动的疲劳损伤计算公式，并结合有限元方法，给出了运载火箭结构在正弦、定频、随机振动载荷下的疲劳损伤仿真分析方法和分析流程。

1 基于Miner线性累积损伤理论的结构振动疲劳损伤计算方法

Miner线性累积损伤理论[8]将疲劳损伤LD定义为使用应力下的循环次数n与该应力下材料疲劳寿命N的比，即：

在多级不同应力幅值作用下，疲劳损伤为

式中in为第i级应力水平下的循环次数；iN为第i级应力水平下的疲劳寿命，损伤小于1时结构不会发生疲劳破坏。

正弦振动过程中振动时间、频率和扫描率的关系为

则，

由以上各式得到的正弦振动时结构的疲劳损伤为

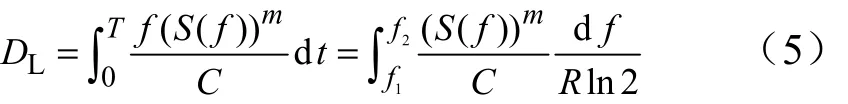
在振动过程中定频振动应力发生的次数为

式中S为每秒内的应力；C为疲劳常数；R为扫描率；f为定频振动频率；T为振动状态的持续时间。定频振动时振动应力为一定值，则定频振动时结构的损伤为

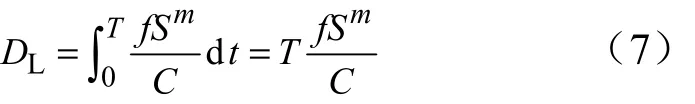
随机振动基于Miner线性累计损伤模型和Dirlik方法，采用3个统计参数从随机振动信号中估计振动应力水平及应力的周期数量[9]，这3个参数分别为均值E( 0)、峰值E(p)和不规则因子γ，定义结构响应的n阶惯性矩为

式中 ()G f为应力谱密度。

则，

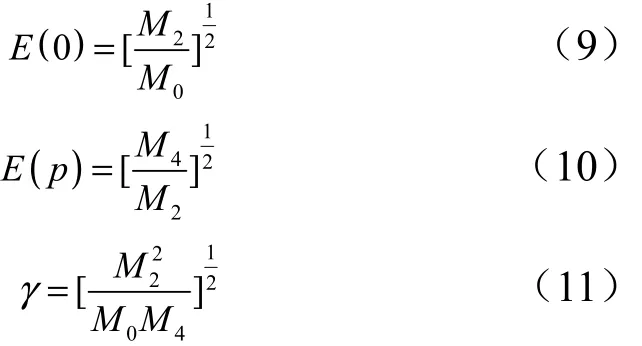
每秒内应力S对应的次数为

根据Dirlik公式有：

得到随机振动时结构的疲劳损伤为

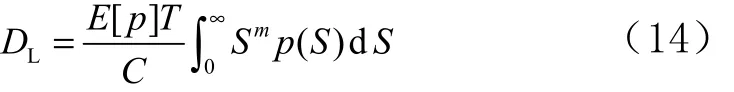
2 基于有限元方法的结构振动响应及疲劳损伤计算

2.1 基于有限元方法的结构振动疲劳损伤分析流程

基于有限元方法的结构振动疲劳损伤分析首先要进行振动载荷作用下结构的动力学响应分析，然后基于动力学响应分析结果进行结构的振动疲劳损伤估算，基于有限元方法的结构振动疲劳损伤一般采用频域分析方法，结构振动疲劳损伤分析流程如图1所示。

图1 基于有限元方法的结构振动疲劳损伤分析流程示意Fig.1 Structural Vibration Fatigue Damage Analysis Process Based on Finite Element Method

2.2 基于有限元方法的结构应力响应分析

本文以管路为例，采用有限元方法计算结构的振动应力响应，管路材料为1Cr18Ni9Ti，管路正弦振动载荷条件如表1所示，定频振动条件如表2所示，随机振动条件如表3所示，振动均为3个方向，管路有限元分析模型如图2所示。

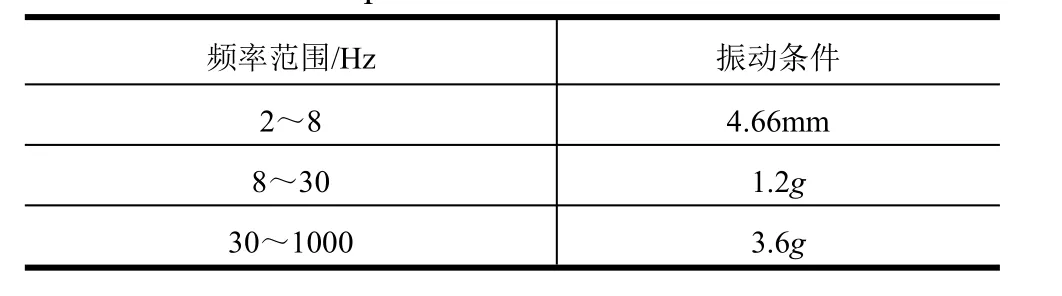
表1 结构正弦振动条件Tab.1 Sinsweep Vibration Conditions of Structures

表2 结构定频振动试验条件Tab.2 Dwell Vibration Conditions of Structures

表3 随机振动条件Tab.3 Random Vibration Conditions

图2 管路有限元分析模型示意Fig.2 Finite Element Analysis Model of Pipeline

管路两端固定，内压1.5 MPa，并在一端施加振动激励，管路结构振动应力响应基于模态动力学分析方法，在求得结构频响函数的基础上，进而求得结构在振动条件下的应力等响应。管路结构部分模态的共振频率和振型分析结果如图3所示。

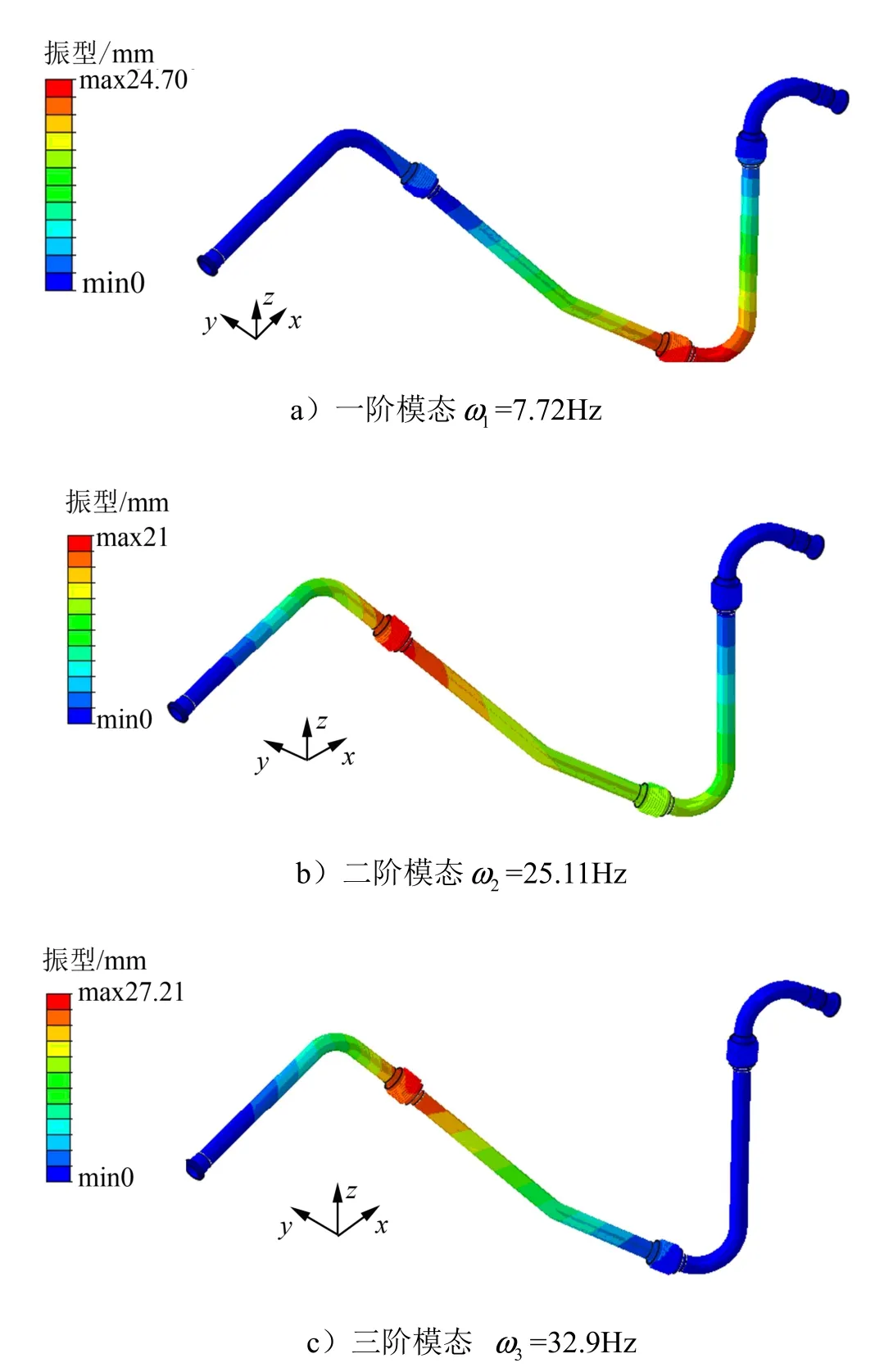
图3 管路模态分析结果Fig.3 Modal Analysis of Pipeline

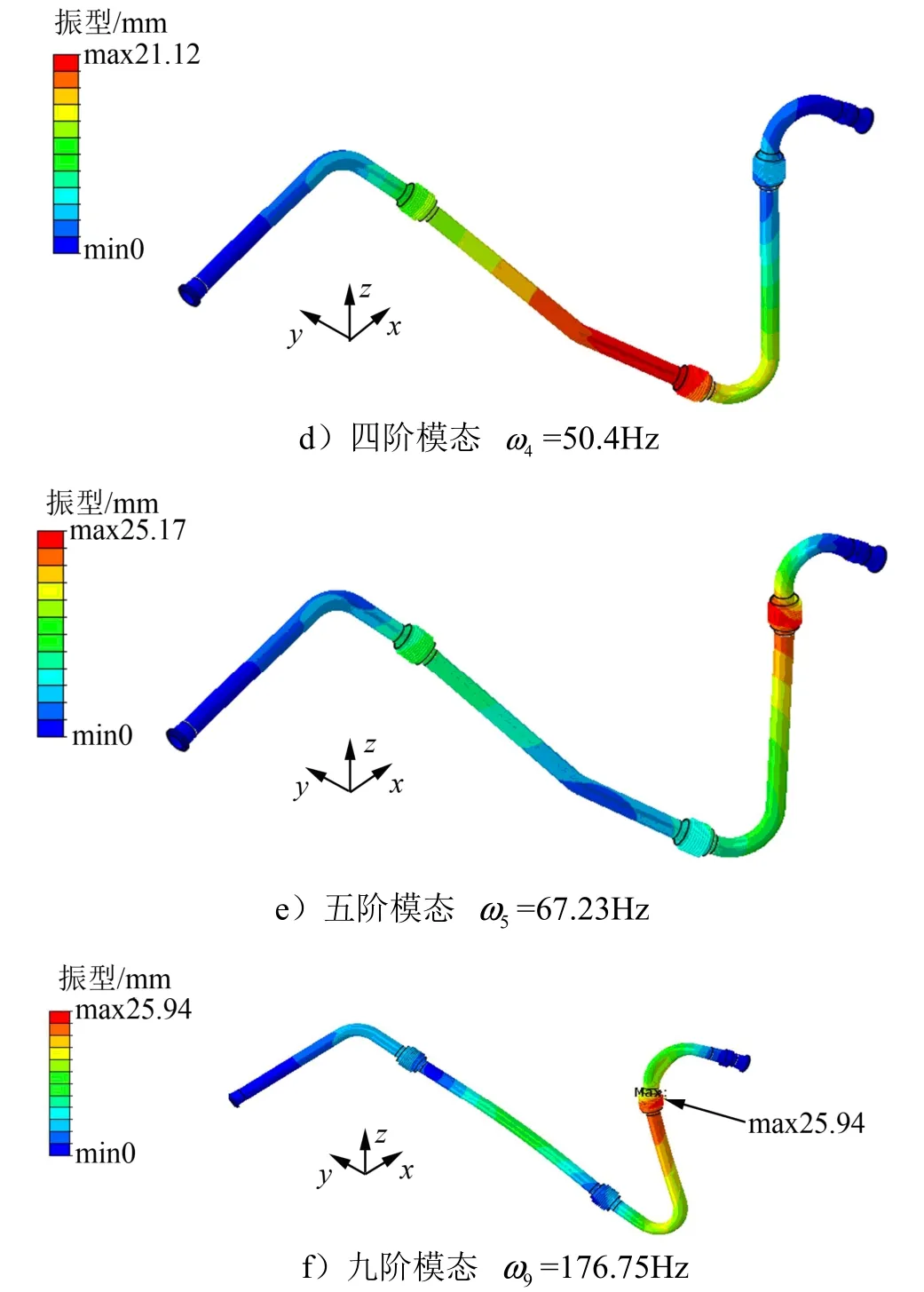
续图3

正弦振动条件下管路应力响应云图及结构应力最大点的应力响应如图4所示。

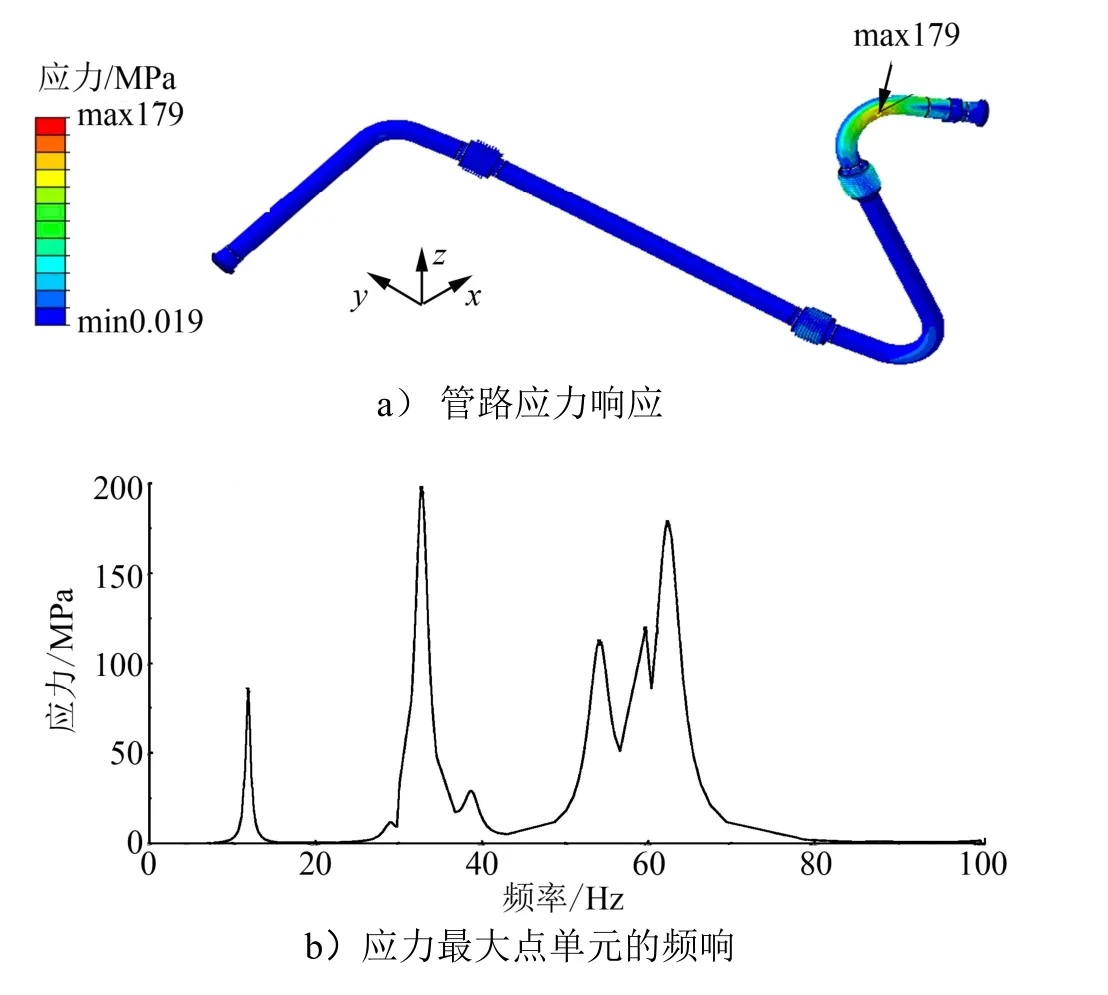
图4 正弦振动管路应力云图及应力最大点单元的频响曲线Fig.4 Stress Cloud Chart and Frequency Response Curve of Sinsweep Vibration Pipeline

由图4可知，管路上最大应力为179 MPa，对应管路的第3阶模态。

定频振动条件下管路应力响应如图5所示。由图5可知，管路上的最大应力为14.9 MPa。

图5 定频振动管路应力云图Fig.5 Stress Cloud Chart of Dwell Vibration Pipeline

随机振动条件下管路应力响应及危险点应力谱密度如图6所示。由图6可知，管路上的最大均方根应力为40.25 MPa，主要是第5阶和第9阶共振频率的激励。

图6 随机振动管路均方根应力云图及危险点应力谱密度曲线Fig.6 RMS Stress Cloud Chart of Random Vibration and Stress Spectrum Density Curve of Dangerous Point

2.3 振动疲劳损伤评估

采用Miner线性累积损伤理论计算结构的疲劳损伤，当损伤LD小于1时，结构一般不会发生疲劳破坏，当损伤LD不小于1时，结构发生疲劳破坏的可能性极高；采用Goodman方法考虑预应力的影响，管路在正弦、定频和随机振动载荷条件下的疲劳损伤计算和试验结果如表4所示。由表4可知，计算结果和试验结果一致，结构在给定的振动载荷下不会发生疲劳破坏。

表4 管路正弦、定频、随机振动疲劳损伤预测及试验Tab.4 Fatigue Damage Prediction and Test of Pipeline under Sinsweep,Fixed Frequency and Random Vibration

3 结论

a）本文基于Miner线性累计损伤理论推导了结构的正弦振动、定频振动和随机振动疲劳损伤计算公式，以管路为例，采用有限元软件，基于模态的动力学分析方法计算了管路结构在正弦、定频、随机振动载荷下的振动响应及疲劳损伤并进行评估，结构不会发生疲劳破坏，与试验结果吻合；

b）本文提出的计算方法和流程可用于指导运载火箭研制工程中结构的振动疲劳损伤分析，具有良好的工程应用价值。