运载火箭推力故障下的弹道重构策略研究

韩雪颖，马 英，程 兴，马忠辉

（北京宇航系统工程研究所，北京，100076）

0 引言

随着航天科技的迅猛发展，对运载火箭可靠性提出了越来越高的要求，发动机作为火箭动力装置，是全箭飞行可靠性及安全性的决定性因素，其可靠性关乎整个飞行任务的成败。在世界航天史上，有很多由于发动机故障导致任务失败的教训，如印度GSLV-F02运载火箭曾因4枚捆绑助推器中的1枚发动机推力控制器发生异常导致推力不对称，进而火箭偏离预定轨道，随即发生爆炸；俄罗斯联盟-U曾因三级发动机燃料管堵塞而失去推力，最终发射货运飞船任务失败等。有故障统计数据表明，火箭动力飞行段大概有60%的故障来源于动力系统[1]，尤其是新研制的发动机，其发射故障的可能性更大。即便如此，随着自适应制导技术的发展，一些运载火箭在发动机故障情况下，通过调整飞行程序，仍能完成入轨。土星I火箭曾在1台发动机因故障提前关机时，通过调整发动机关机时间成功进入预定轨道；德尔塔4在发射第3颗GPS-2F卫星任务中利用制导系统重新生成飞行轨迹，对上面级发动机故障时的推力下降进行了及时补偿，充分利用剩余燃料成功完成卫星入轨；法尔肯9火箭首次执行国际空间站商业货运任务时，通过在线规划新轨迹，在损失1台发动机推力的情况下依然出色完成主要任务。

中国针对适应一定发动机故障的制导技术已有多年研究，包为民[2]指出了用于解决控制系统高可靠性、故障下的可重构飞行控制等基础问题的关键技术，未给出详细方法；王文虎[3]等针对亚轨道飞行器（SRLV）应急返回任务提出了一种用于发动机推力常值损失下的正攻角飞行程序设计方案，使得不同故障时刻SRLV均能安全达到低动压环境；陈新民[4]、吕新广[5]等通过深入研究得出迭代制导对火箭动力系统故障具有很好适应性的结论。目前，中国载人运载火箭长征2F，及其它多型运载火箭均使用了迭代制导技术，可以适应多种推力下降故障，但容错能力仍然有限。如何在不增加硬件设备的情况下，进一步提升火箭飞行可靠性，亟待研究解决。

本文针对某型运载火箭发动机推力下降的故障问题，分析迭代制导的故障适应性，提出一种基于迭代制导算法的弹道重构策略，并通过数学仿真验证该策略的有效性。

1 发动机推力故障模型

本文所考虑推力下降故障模式为发动机在稳定工作段的某时刻，推力迅速下降到一固定值，此后发动机推力保持该固定值，表征该故障的特征参数主要有故障发生时刻和发生故障后发动机输出推力大小。以某型运载火箭芯一级两台发动机为例，各台发动机发生推力下降故障后的推力数学模型为

在故障仿真计算时，为了获得箭体系中的视加速度，需要计算推力矢量在箭体系中的分量。对于单台发动机而言，其推力通常是沿发动机轴线方向，由于发动机安装角、摆角等的存在，这样的推力矢量并不在箭体系中，因此需要进行一定的转换。本文通过发动机通用建模，精确地实现了这一转换，同时解决了发动机故障灵活注入的问题。首先，引入发动机坐标系，其坐标原点O位于喷管摆动质量中心，x轴由坐标原点指向摆动轴，y轴垂直于喷管摆动平面并指向火箭轴线，z轴按右手法则确定。箭体坐标系至发动机坐标系的转换过程及转换矩阵egbM 为

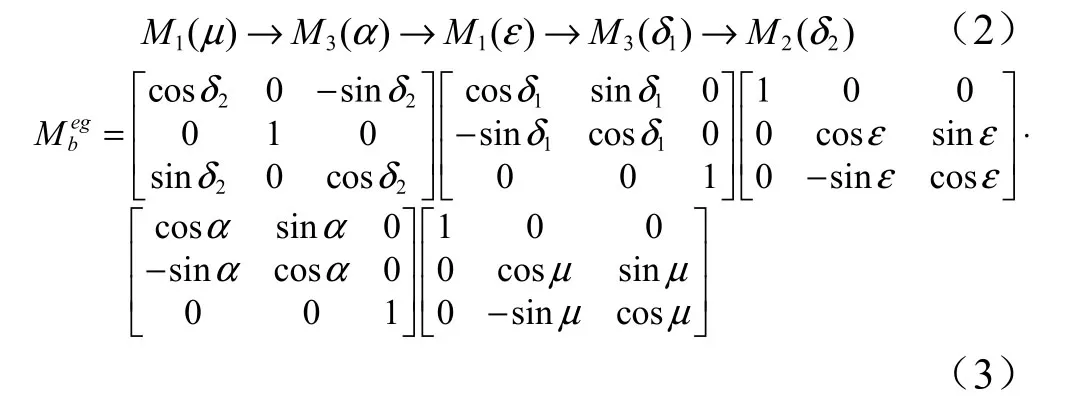
式中 µ为发动机安装象限角，I象限为0°，从火箭尾部看，顺时针为正；α为发动机安装角；iδ（i=1，2）为发动机摆角，1δ为绕z轴的转角，2δ为绕y轴的转角；ε为发动机旋转角，是1δ摆动方向与y轴之间的锐角夹角，它是为适应发动机两种摆动方式“径向、切向摆动”和“十字摆动”而产生的角度定义，其示意图分别见图1a、图1b。

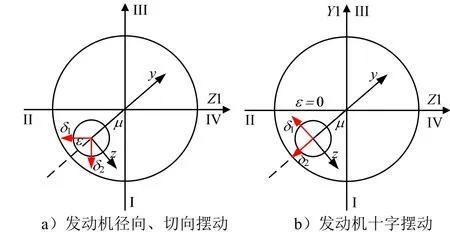
图1 发动机旋转角示意Fig.1 Schematic Diagram of Engine Rotation Angle

每台发动机的推力P分解到箭体坐标系，可由下式得到：

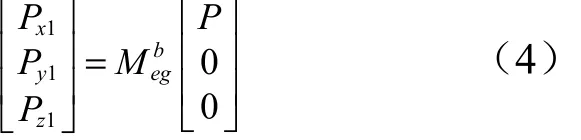
式中 Px1, Py1, Pz1为发动机推力P在箭体坐标系3个方向的分量；为发动机坐标系到箭体坐标系的转换矩阵，

2 基于迭代制导的弹道重构策略

2.1 迭代制导的故障适应性分析

如果发动机发生故障，传统基于标准弹道的摄动制导方法更加适应小偏差情况，其故障适应能力偏弱，因此需要引入能够在线生成轨迹的自适应制导方法。文献[6]中指出迭代制导能够适应较大程度、多种形式的发动机推力异常。迭代制导作为自适应制导方法的一种，在国内外运载火箭上得到了成熟广泛的应用，它是以火箭瞬时状态为初值，入轨点状态为终端约束，瞬时点到入轨点的剩余飞行时间最短为性能指标的最优控制问题[7]。但对于处理速度和存贮容量有限的箭载计算机而言，在火箭飞行过程中，无法实时计算出该问题的最优解，只能根据任务性质和精度要求采取近似处理的方法。文献[8]中给出了在真空飞行段，迭代制导近似最优控制解的表达式

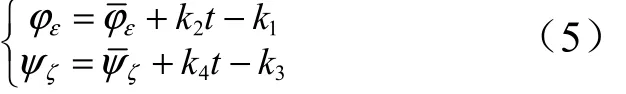
在火箭飞行过程中，迭代制导利用箭载导航设备实时测量视加速度信息并进行简化积分，实现对入轨点速度、位置的预估。当发动机发生故障时，箭载计算机可根据所测视加速度信息敏感推力变化，并通过调整剩余飞行时间和式（5）中的1k，2k，3k，4k，实时计算最优推力矢量方向，进而在线生成新的最优飞行轨迹，且只要运载能力具备，入轨精度满足要求。

2.2 弹道重构策略设计方案

针对某种程度的发动机推力下降故障模式，火箭在富余运载能力不多的情况下，利用剩余飞行能力将无法进入预定轨道，但可以进入某过渡轨道，此类故障即属于非致命故障。处于该故障情况下的飞行任务并非无法挽救，但由于随故障程度的不同，所形成的过渡轨道不是固定的，故不利于有效载荷事先制定应急救援措施。设计流程图见图2。

图2 弹道重构设计流程图Fig.2 Flow Chart of Trajectory Reconfiguration

挽救此类故障任务需要进行弹道重构设计，基本方案如下：

a）建立地面弹道库。梳理发动机典型故障模式，通过综合考虑运载火箭能力富余情况和有效载荷自救能力，预先确定救援轨道，此轨道应是允许有效载荷无动力飞行并维持数天的低轨道，且数量有限；同时，针对典型故障工况，以救援轨道为目标轨道开展重构弹道优化设计，生成重构诸元，编排诸元切换策略，并进行充分的地面验证；

b）能力预测。对于火箭末级飞行段，基于当前速度位置信息和故障诊断出的发动机推力下降程度，实时计算到达原定轨道所需要的推进剂量、速度增量等表征剩余飞行能力的特征参数，并与遥测数据计算的特征参数比较，如果高于所需剩余飞行能力，则可采用迭代制导按照原定轨道实时生成最优飞行轨迹；如果低于所需剩余飞行能力，则根据救援轨道最低能力需求确定是否能够进行轨道降级，如不满足该需求，则发出“救援轨道不存在”指令；如满足，则可根据实际剩余飞行能力选择救援轨道进行轨道降级；

c）执行重构策略并进行诸元切换。针对某些故障模式，地面应通过执行重构策略，选择确定重构诸元，并具备诸元上传的功能。箭上制导系统以上传的重构诸元为目标，通过迭代制导进行弹道重构，在线规划新的飞行轨迹，将有效载荷送入救援轨道，为后续救援、有效载荷变轨提供最好的条件。

对于非末级飞行段的故障，由于需要考虑的约束较多（如落点约束、qα约束等），如果将火箭剩余飞行的全弹道进行规划，可能会带来效率等方面问题，故尽可能维持标准弹道飞行，在本飞行段关机点由故障产生的偏差由其上面级飞行段补偿，在非末级飞行段不进行救援轨道的确定。

3 仿真验证

以某型运载火箭发射42°倾角、200 km×400 km LEO近地轨道为研究对象，针对火箭飞行过程中不同时刻出现发动机推力下降为零的故障模式，对本文提出的弹道重构策略进行分析验证。

3.1 故障情况下迭代制导的适应性

分别考虑单个助推器发动机、芯一级发动机、芯二级发动机在不同时刻推力下降为零，得到故障适应性分析结果见图3。

图3 中“故障发生时刻”是以各飞行段起始时刻为0 s。

以上结果表明，在不采取任何补救措施的情况下，迭代制导对故障的适应能力是有限的，且存在火箭最终无法进入预定轨道、但可进入某过渡轨道的中间状态。不考虑各项偏差项，以芯一级发动机分别从50 s、120 s、140 s开始推力下降为零的故障模式为例，相比无故障状态，其零干扰弹道的速度、高度对比曲线见图4、图5。以预定轨道为目标的零干扰弹道入轨参数偏差见表1。

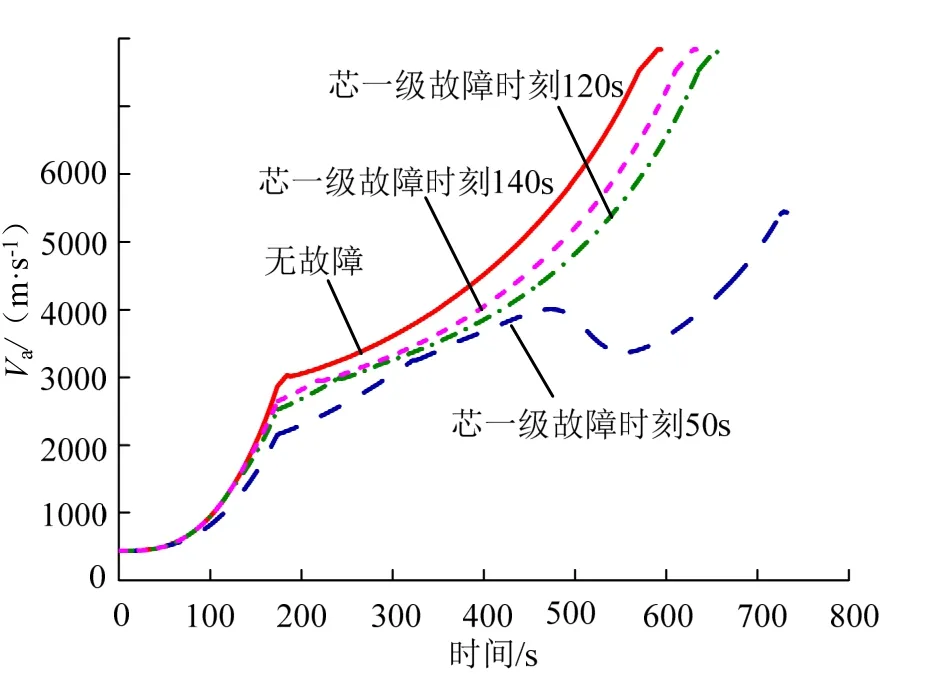
图4 时间-速度曲线Fig.4 Curve of Speed and Time

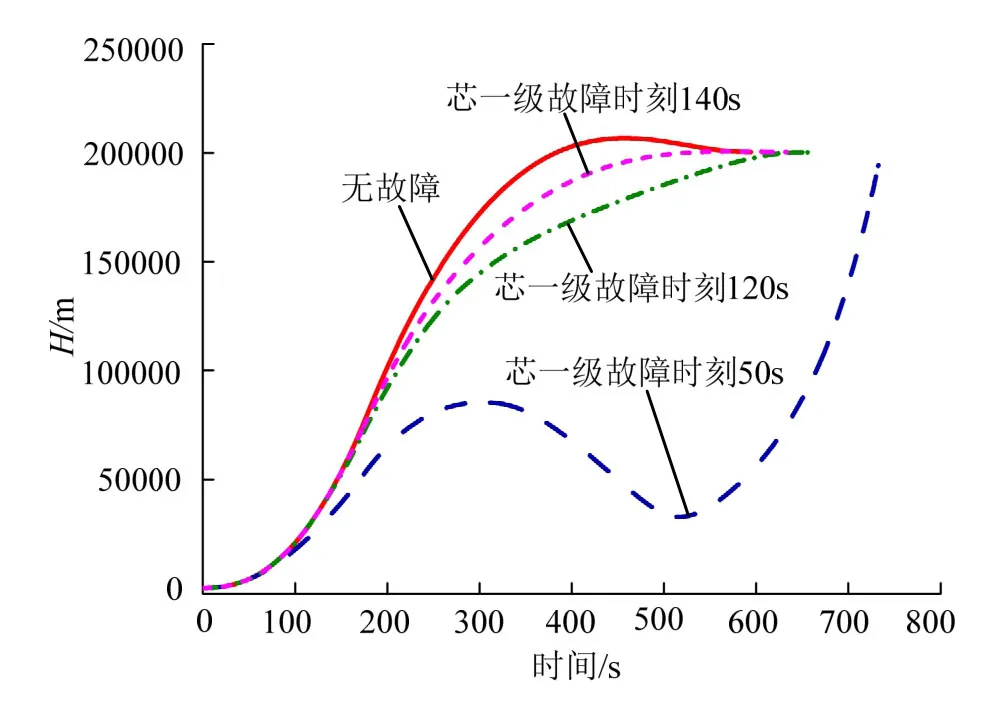
图5 时间-高度曲线Fig.5 Curve of Height and Time

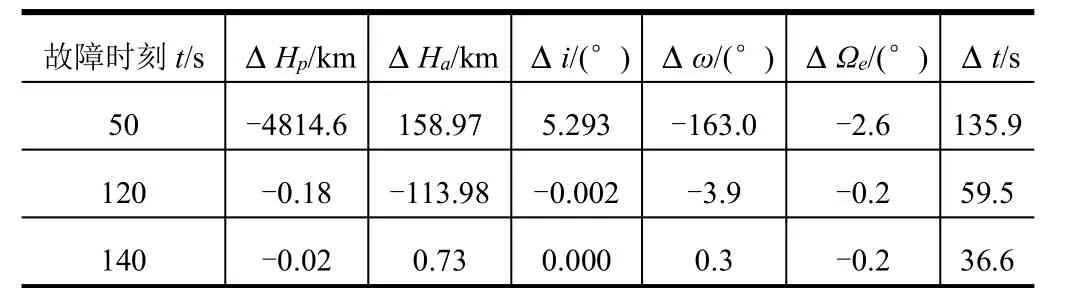
表1 零干扰弹道入轨参数偏差Tab.1 Injection Parameter Deviation of Zero-bias Trajectory

从图4、图5和表1可以看出，芯一级单台发动机在起飞后50 s开始推力降为零，致使火箭运载能力损失较为严重，仅依靠迭代制导无法适应，最终入轨参数偏差较大，不能形成轨道，无法挽救；120 s开始推力降为零，入轨参数有一定偏差，可以形成轨道，最终进入200 km×271 km的过渡轨道，若再考虑实际飞行过程中干扰的作用，很可能因运载能力不足而导致任务失败，但依然存在挽救的可能；140 s开始推力降为零，采用迭代制导，通过延长入轨时间，可以自适应进入预定轨道，入轨参数偏差满足要求。助推器、芯二级各颜色区域故障情况与芯一级类似，不再赘述。

3.2 救援轨道设计及策略编排

结合能力预测情况，选择确定42°倾角、150 km×200 km 的低轨道为救援轨道，并根据图3分析结果，针对以下临界状态设计重构弹道：a）助推飞行140 s，一个助推发动机推力降为零；b）芯一级飞行120 s单台发动机推力降为零；c）芯二级飞行100 s单台发动机推力降为零，并生成重构诸元。为便于描述，将原定诸元称为“0”号诸元，按照a）、b）、c）生成的诸元分别称为“1”、“2”、“3”号诸元。重构弹道与原弹道俯仰程序角对比曲线见图6。针对单台推力降为零的故障模式，诸元切换策略编排见表2。

图6 俯仰程序角对比Fig.6 Pitch Angle Comparison

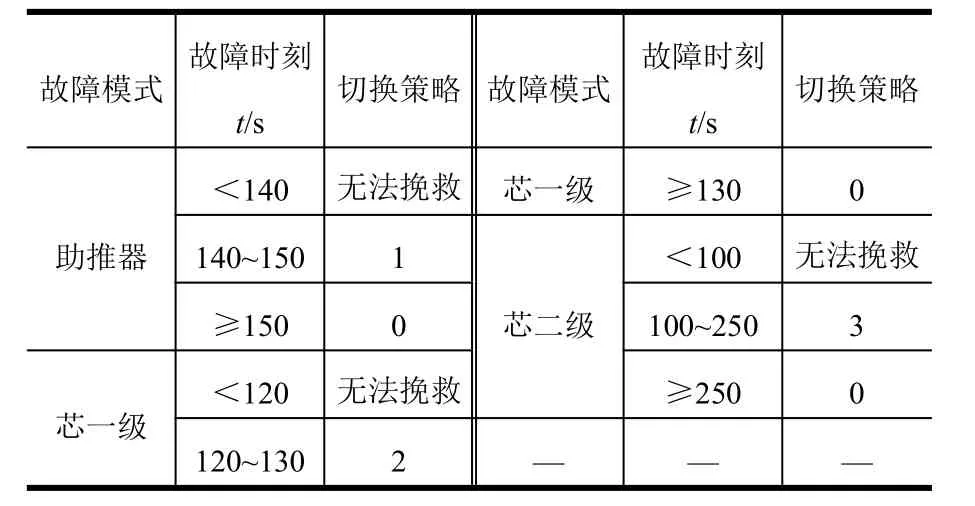
表2 诸元切换策略Tab.2 Data-switching Strategy

3.3 弹道重构后的适应性

采用本文提出的故障重构策略对图3中能够形成轨道的各故障任务（黄色区域）进行适应性分析，得到图7的统计结果。

图7 故障适应性分析结果（切换诸元后）Fig.7 Analysis Results of Fault Adaptability(After Switch of Data)

以3.2节中能够形成轨道的a）、b）、c）3种临界状态为例，采取表2的诸元切换策略，其速度、高度随时间变化的曲线，见图8、图9。

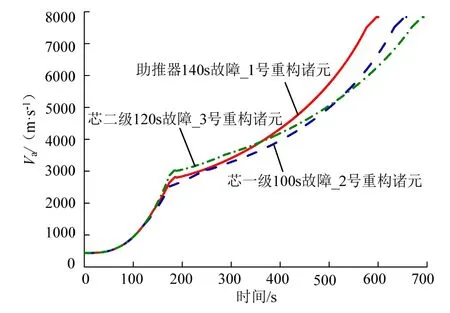
图8 时间-速度曲线Fig.8 Curve of Speed and Time

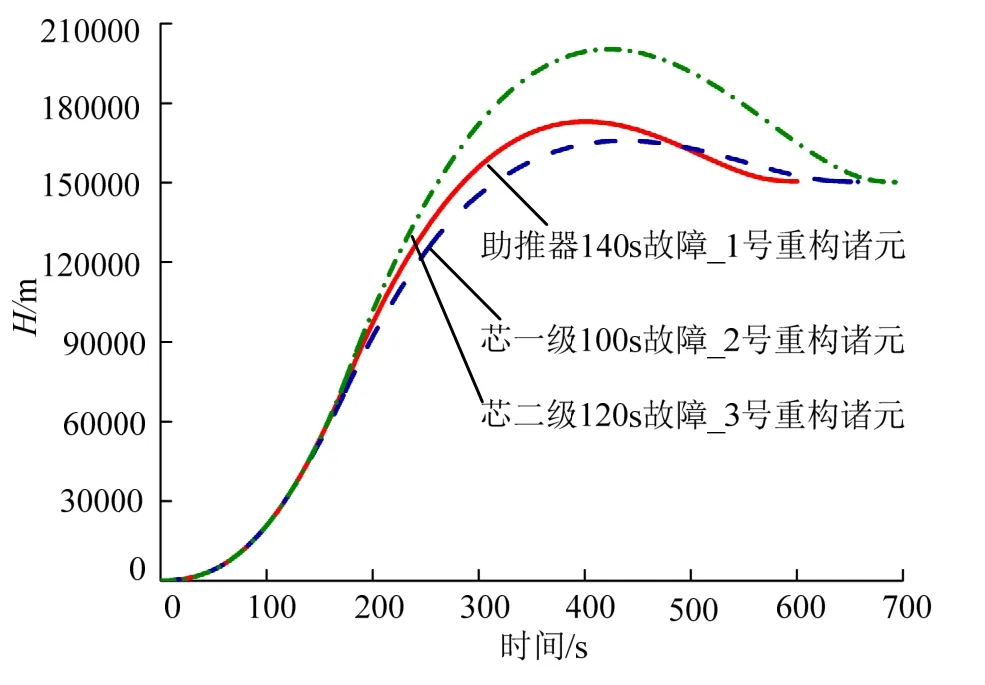
图9 时间-高度曲线Fig.9 Curve of Height and Time

以救援轨道为目标的零干扰弹道入轨参数偏差见表3。

从图7～9及表3中的适应性分析验证结果，采取本文提出的故障重构策略后，图3结果可知无法进入预定轨道、但可以进入某过渡轨道的状态，通过合理切换诸元，采用迭代制导进行弹道重构，最终能够进入救援轨道，从而验证了本文策略的有效性。

4 结论

本文针对运载火箭发动机推力下降故障，提出了一种基于迭代制导的弹道重构策略。仿真结果表明，对于仅依靠迭代制导无法进入预定轨道、但可进入某过渡轨道的故障任务，通过使用本文策略，合理切换诸元，可在迭代制导的作用下将有效载荷安全送入救援轨道，为后续有效载荷自救提供了可能，拓展了航天发射任务的故障适应范围，降低了坠落等重大风险，提高了全箭飞行可靠性，具有工程应用价值。此外，对于故障诊断、能力预测及救援轨道的优化设计方法还将进一步开展深入研究。