动物种群动态模型研究的进展与展望

席唱白, 迟瑶, 钱天陆, 盛彩英, 王结臣,3,*



动物种群动态模型研究的进展与展望

席唱白1,2, 迟瑶1,2, 钱天陆1,2, 盛彩英1,2, 王结臣1,2,3,*

1. 南京大学地理与海洋科学学院 南京 210023 2. 江苏省地理信息技术重点实验室 南京 210023 3. 江苏省地理信息资源开发与利用协同创新中心 南京 210023

动物种群动态模型经历了百余年的发展, 文章回顾和总结了其取得的丰富成果, 并展望其未来发展方向。种群动态包括种群数量动态和时空分布动态, 根据其形式和研究内容，可以将种群动态模型分为数量模型和空间模型。数学模型通过数学方程模拟种群数量的变化趋势, 它包括“J”型增长模型、“S”型增长模型和Lotka-Voltera模型等; 空间模型侧重于种群和生境的空间化表达, 包括异质种群模型、空间精确性种群模型和基于个体的种群模型等。种群动态模型在物种保护、气候变化和土地管理等方面都有成功应用。目前, 种群动态模型的空间描述能力不足, 未来与地理信息技术结合将有助于种群动态模型的进一步发展。

地理信息系统; 种群动态; 空间模型; 物种分布模型; 动物保护

0 引言

种群动态变化一直是人们关注的焦点[1-2]。种群动态包括种群数量动态和时空分布动态[3]。野生动物是地球生态系统的重要组成部分, 是大自然赐予人类的宝贵财富。种群动态研究可以帮助人们认识种群变化规律, 为动物保护和构建人与自然和谐相处的环境提供决策支持和科学依据。

种群动态模拟经历了两个关键阶段。十九世纪二十年代开始, 人们将统计学和微分方程引入到生态学中, 通过数学表达式模拟物种数量变化情况。通过数学模型逐步认识了种群各种特征对种群数量变化的影响。然而将种群分布简单抽象为数学上的概率分布不足以满足种群动态学的要求。十九世纪六十年代之后, 计算机的出现推动了许多学科的发展, 也为种群动态模拟带来了新的动力。随着生态学定量化和模型化的趋势, 学者们探索和开发了许多新的空间模型[4]。

种群动态模型的发展也面临着新的机遇。十九世纪七十年代年以来, 地理信息系统(Geographic Information System, GIS)快速兴起, 为包括动物地理在内的各类空间现象研究提供了先进手段。以空间数据管理和空间分析能力见长的 GIS 技术、大数据时代丰富的多主题对地观测可共享数据, 为从宏观上开展种群动态的综合研究奠定了数据和技术基础。本文梳理了GIS在生态学和种群动态研究中取得的一些成果, 结合种群动态的经典模型, 回顾和总结了种群动态的发展过程。

1 种群动态数量模型及其发展

从1798年开始, 种群动态开始受到学者关注。最初的种群动态模型主要关注种群的数量变化趋势, 可以称之为数学模型。数学模型分别从不同的角度研究了种群内部结构或种群迁移等种群特征对数量动态的影响。许多研究用数学模型来预测种群个体数量变化趋势。最初, 研究者建立某种群特征驱动的种群数量动态的微分方程, 研究种群数量随该因素的变化规律; 后来同时融入多种种群特征的偏微分方程、随机种群动力系统等用于多因素种群动态模拟, 数量模型也变得更加丰富和完善。数学模型的产生为生物学家提供了种群研究的科学方法, 为深入研究种群动态变化奠定了基础。

1.1 指数增长模型

Malthus在1798年的著作《人口原理》中第一次应用指数增长模型表示人口数量变化[5]。通过分析百余年的人口统计资料, 他发现人口自然增长过程中, 增长速率可视为一个常数r, 并以此建立了数量模型。Malthus模型是在理想条件下, 种群数量的增长与物种的繁殖能力有关。对于世代不连续的物种, 假设种群的每代增长率为, 用差分方程表示为N+1=λN; 对于世代连续的种群, 种群数量时刻发生着变化, 在某一瞬间变化率与当前种群数量成正比, 用微分方程表示为d/d=λ, 积分可得

=oe。

其中,表示时刻的种群数,o表示初始时刻的种群数量,称为种群内禀自然增长率。内禀增长率是物种的固有特征, 受一系列形态、生理特征所决定, 它是在进化过程中物种所形成的种群的潜在增长能力, 也称种群的生殖潜能或生物潜能。当>1时, 由Malthus模型模拟得到的种群数量呈指数型增长, 图形曲线接近“J”型, 因此又称为J型增长模型。

1.2 “S”型增长模型

1838年德国人韦尔胡斯特首先提出了Logistic方程[6], 它是对指数增长模型的重要改进。该模型认为由于资源限制, 在一定的环境下种群增长率随种群数量的增大而减小。不同环境条件下, 都存在一个环境容纳量K, 它表示环境所能承载并且保持健康稳定时的最大种群数量, 当种群数量达到K时, 种群不再增长。这种种群增长趋势可以用用微分方程表示:

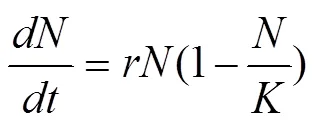
式中表示当前种群数量,为环境容纳量,为种群内禀自然增长率。Logistic模型的曲线呈“S”型, 因此, 又叫S型增长模型。

1920年, Pearl应用“S”型增长模型对美国几十年间的人口变化进行拟合, 发现美国人口数量在增长过程中, 增长率不断减小, 符合“S”型变化规律[7]。随后分别模拟了美国黑人和白人数量的变化, 发现其均符合“S”型增长曲线[8]。Monk等以纽约和芝加哥地区为例, 研究精细尺度下的人口变化规律, 数量模型一时成为学者们的研究热点[9]。

1.3 Lotka-Voltera模型

Lotka-Voltera模型分别由美国学者Lotka和意大利学者Voltera在1925和1926年提出。它主要考虑了种群竞争关系, 包含两种群之间对环境资源的竞争, 如食物、空间、水等, 但两者之间不存在捕食寄生等关系。模型假设在同一生境下, 生活着两个对某种资源相互竞争的种群, 若两种群间不存在相互作用, 种群增长率与当前种群数量、环境容纳量和种群内禀增长率三个变量有关, 可用Logistic方程表示如下:

然而当两种群存在竞争时, 会导致压缩彼此的空间容纳量, 并且增长率速度受到对方的限制。对物种甲来说, 物种乙的存在会占用甲的尚未利用空间, 相当于压缩了甲的环境容纳量。因此, 考虑甲的种群增长率时需要计算乙相对于甲的种群数量的当量同理计算乙的增长率。甲乙相对彼此的当量如下:

1=2

2=1

1、2为当量的种群甲的数量,、为折算比例。由此可得:

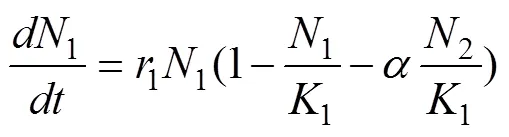
这就是著名的洛特卡-沃尔泰拉种群竞争模型。

数学模型种类繁多, 以上介绍了几种代表性的模型, 奠定了种群动态模拟的基础。但是可以看出, 数学模型都建立在极为理想的假设条件下, 它将复杂的种群特征, 如出生、死亡、迁移和繁衍等简化为内禀增长率, 将物种生境条件简化到环境容纳量上来。事实上, 种群动态变化并不是简单地通过内禀增长率和环境容纳量就可以解释。从微观角度看, 种群由大量个体组成, 个体随机运动造成了种群表象上的特征。大量微观组分的随机运动导致宏观整体的某种规律的现象称之为扩散, 由此美国学者Fisher在1937年提出了一维空间中的种群扩散动态模型[10]。物种的种群结构也各不相同, 其中性比对种群动态的影响是不可忽视的部分。此外, 物种都可能具有独特的生活史特征, 比如鸟类的性比随着年龄的变化会出现较大差异, 而且雌雄两性可能具备不同的死亡率、迁移率等[11], 刘汉武以此结合Lotka-Voltera模型提出了具性别结构的食饵-捕食者模型[12]。数学模型经历了百余年的发展, 取得了丰硕的研究成果的同时, 还在不断的丰富和完善。

2 种群动态时空模型及其发展

在1970年前, 种群动态模拟都是以数学模型的形式, 然而种群的生存和繁衍与栖息地生态环境息息相关。随着科学技术的发展, 种群动态模拟不仅限于理想化的数学模拟, 叠加生境模拟功能的空间化模型开始出现。这标志着种群动态模型开始偏重于空间动态的研究, 我们称之为空间模型。空间模型的发展中, 影响最深远的是异质种群模型, 它首次考虑种群生境因素, 认为物种分布在若干异质性生境斑块中, 物种在各斑块间迁移; 随后产生了将生境具体化和现实化的模型, 如直观种群模型和基于个体的种群模型等, 使种群动态研究更深入。至此空间模型也具备了良好的实用性, 被广泛应用在生态学各个领域。

2.1 异质种群模型

1970年Levins最早提出了异质种群模型, 也有译作复合种群、集合种群或超种群[13]。异质种群模型最先引入了种群相对位置和距离的概念, 它主要考虑同种物种常常生活在不同的生境斑块中, 并且相互之间靠动物迁移维持联系[14]。不同斑块的种群因为环境适宜程度差异, 在迁入、迁出率上存在差别。异质种群模型的简单形式如下:

其中,为生境斑块所占比例,为动物在斑块之间的扩散率, e为种群灭绝率。

多种科学领域的学者根据需要将异质种群模型融入自己的研究中。二十世纪九十年代, Hanski等为15 km²内50个生境斑块内川贝蝴蝶的种群构建了结构化的异质种群模型, 在该研究中, 采用标记重捕法验证了川贝蝴蝶在斑块间普遍的迁移现象, 然后分析了斑块种群密度差异与生境特征的关系, 该模型成功证明了种群动态在斑块间存在动态平衡的合理性[15]。Marsh研究了两栖类物种的分布动态, 认为将池塘视为异质种群模型中的生境斑块的观点是合理可行的, 然而发现物种在斑块内灭绝的原因可能不是迁徙, 而是环境干扰, 并提出两栖动物保护的关键在于生态环境质量[16]。Verboom等对欧洲五子雀进行了研究, 认为每个斑块的局部灭绝率不是恒定的, 而是取决于斑块尺寸和斑块质量, 该研究考虑了生境斑块现实因素, 如斑块尺寸、栖息地质量和斑块隔离等对种群定殖率和灭绝率的影响[17]。

2.2 空间精确性种群模型

种群都有各自的生境空间, 包括特定种群的栖息地特征, 如地貌形态、植被景观结构和斑块分布等, 具有生境特征的种群动态模型就称为空间精确性种群模型(Spatially Explicit Population Model, SEPMs)[18,19]。模型将生境分为不同景观斑块, 通常认为斑块内是同质的。SPEMs有两个重要的指标: 粒度和范围。粒度是最小斑块的大小, 粒度越小则斑块之间的差异越准确, 它体现了模型的精度; 范围表示了模型的研究尺度。

空间精确性种群模型被认为是种群生态学家、生物保护学家和土地管理者认识自然景观配置和种群动态间复杂关系的重要工具[20]。Moen等将景观的结构和觅食、运动能量等结合起来开发出EASE模型, 模拟驯鹿在不同季节的活动, 进一步研究觅食策略和生存繁衍情况[21]。Wiegand根据在澳大利亚和斯洛文尼亚的实地调查数据构建了空间精确性种群模型, 并预测种群数量变化趋势, 分析了小种群面对威胁而灭绝的可能性[22]。JOEL通过高精度大范围的随机运动模型模拟了阿根廷蚁的活动, 获得了其入侵模式和扩散趋势[23]。国内学者程远峰也利用SPEMs进行了研究, 他开发出易泛滥成灾的野生动物种群动态监测系统, 分析生境质量和面积对野猪数量变化的影响, 为生境保护提供决策支持[24]。

2.3 基于个体的种群模型

基于个体的模型(Individual-Based Models, IBMs)最早在1990年被开发并应用于大眼梭鲈数量的研究中[25]。区别于空间精确性种群模型强大的生境模拟能力, IBMs主要实现了动物的个体行为空间化: 以组成种群或种群集合的个体为对象, 每个个体拥有独特的属性特征, 以及与环境、系统中其他个体间独特的交互方式, 通过个体的发展变化, 获得种群的时空格局[26]。

目前已有很多IBMs的应用案例, 在渔业管理、森林动态、同域物种演化、集合种群动态、种群多样性和保护等广泛领域内取得成功应用。Fahrig采用基于个体模型模拟了虚拟物种繁殖、死亡、运动过程, 探究出生率、扩散率、栖息地质量、栖息地空间模式对种群灭绝阈值的影响[27]。有研究通过模拟个体寻找配偶、繁殖、分娩扩散和死亡过程, 探究扩散距离和寻找配偶能力对种群扩散的影响[28]。Letcher的研究基于红顶啄木鸟15年的观测数据和栖息地空间分布数据, 模拟不同个体出生、扩散、繁殖、死亡的生命过程, 探究栖息地斑块数量和空间分布对红顶啄木鸟种群的影响[29]。我国学者陈求稳等以优势种草鱼和鲫鱼为研究对象, 建立了一维全河流和二维局部河段的水环境模型, 考虑鱼的生长和运动两个过程, 模拟了自然条件和水库调节作用下河道的水环境条件, 以及相应的鱼类生长和分布的变化, 探究水库运行对鱼类种群的影响[30]。

空间模型的出现标志着种群动态学研究方式的转变, 具有重要意义。种群动态模拟经历了从数量模型到空间模型的转变, 它创造了一种将种群生态学理论融入现实情景, 使模拟效果更加准确的研究方法。同时, 研究视角也产生了由上而下的转变, 从群体特征转移到个体行为学和生活史特征。Levins的异质种群模型概念较为简单, 它是对种群动态时空分布模拟的有益尝试。随后产生了空间精确性种群模型和基于个体的种群模型, 它们分别加入了空间化的生境信息和个体行为轨迹等, 使模型变得更为现实和使用, 为生态学家和物种保护的决策者提供了重要工具。

3 GIS支持下动物种群动态模型的发展

随着经济高速增长, 生态环境问题凸显出来, 动物种群生存和延续也面临严重威胁。新形势下如何准确模拟种群动态是学者们需要面对的难题。然而, 鉴于GIS强大的空间分析功能和在各领域的成功应用, 本文认为与GIS结合有助于种群动态模型的进一步发展。GIS是在计算机硬、软件系统的支持下, 应用系统工程和信息科学理论, 科学管理和综合分析具有空间内涵的地理数据, 以提供规划、管理、决策和研究所需信息的技术系统。GIS最突出的功能是综合分析空间和属性数据的功能, 包括分类、提取、测量、图形处理、分层、叠加、数据地形分析、多边形叠置分析、统计分析和决策支持等。它将现实世界转化为信息世界, 在计算机支持下, 实现对各种数据信息进行精确而快速的综合处理与分析。GIS的栅格和矢量数据可以准确描述任意形状、任意类型的生境斑块, 同时具有时间序列数据的处理能力, 适合用于空间模型的构建。

3.1 生态学与GIS结合的案例——物种分布模型

物种分布模型(Species Distribution Models, SDMs)是GIS技术和生态学结合的成功案例。SDMs用于探测物种潜在栖息地, 由于栖息地适宜度可能对种群动态产生重要影响, SDMs将成为未来种群动态模拟中是不可或缺的一部分。物种分布模型是基于生态位理论和机器学习方法的预测模型, 它通过观测点数据, 推测物种在生态位空间或环境空间中的分布[31]。SMDs在近二三十年来取得了长足的发展, 产生了多种模型, 包括生物气候分析系统(biocli­mate analysis and prediction system, Bioclim)[32]、最大熵模型(maximum entropy modeling, Maxnet)[33]、广义线性模型(generalized linear model, GLM)和广义可加模型(generalized additive model, GAM)[34]等。

物种分布模型广泛应用在植物和动物的地理分布研究中。宓春荣将精确采样数据和物种分布模型结合, 快速有效地获取了黑颈鹤与白头鹤的地理分布, 该方法相比于传统野外调查节省了大量人力财力[35]。翟天庆采用BIOMOD模型计算了濒危动物朱鹮当前和未来几十年内的分布范围, 此研究为朱鹮的保护提供了可贵的对策[36]。物种分布模型也在气候变化等关注热点领域做出了重要贡献。Houghton等采用物种分布模型模拟气候变化对物种分布范围的扩张和收缩情况, 证实了气候对物种分布有重要影响[37]。沈涛等人利用MaxEnt模型, 以及230条分布数据和33个气候因子, 模拟了红花龙胆在全新世、近代和未来的分布, 认为气候变暖增大了红花龙胆的适宜生境面积, 有助于其向高海拔地区扩张[38]。

3.2 种群动态模型发展展望探讨

种群动态是一个复杂的变化过程, 它和种群自身特征、环境、气候、人为影响以及物种相互关系等密切相关[39-41]。种群动态模型旨在探索种群在各种生存条件下的动态变化, 处于不断发展完善的过程中。无论数量模型还是空间模型, 都是研究种群数量动态变化规律的重要工具, 推动了学者对生物种群内部作用和响应外部环境机制的理解。从数量模型到众多空间模型的产生, 标志着对种群生态的研究由浅入深, 由简单到复杂的过程。

(1)在空间信息获取技术支持下, 获取丰富的动物种群动态参数和生境特征成为可能, 它包括丰富的环境因子数据和全面的生活史参数。目前, 物种分布、种群监测、生境监测等有很多空间信息技术支持。首先, 许多先进技术如GPS和红外相机等已经用于动物种群监测。传统方法往往通过粪便、食物残渣、尸体、足迹等来辨别动物, 通过动物遗迹的出现频次来推测动物数量和生活习性。这种方法存在一些问题, 如实施困难、容易遗漏、数量推测不准确等。GPS和红外相机的应用则有助于简化种群监测问题。GPS可以完整记录动物的活动轨迹, 能快速准确的捕捉动物活动规律。红外相机则自动拍摄路过镜头前的大型动物, 多用于观测动物种群多样性。第二, 遥感技术和由各种传感器搭建而成的环境监测网络迅速发展, 为构建综合的种群动态模拟模型奠定了基础。此外, 遥感技术具有大范围、高精度及高时效的特征, 可以帮助人们获取地形、植被类型、气候等完善的生境要素。最后, 种群观测技术和GIS可以为物种建立空间数据库, 记录种群位置、数量、年龄结构和生境特征等信息, 极大的方便了观测数据的管理、共享和充分利用, 为保护动物学家和管理者提供有力的技术支持。韦月鸾等[42]通过GPS定位、生境拍照技术观察记录了5年内白鹇种群数量和栖息地监测数据, 建立保护动物地理分布信息管理系统, 并分析和预测了种群分布情况。赵德怀等[43]应用GIS技术对1998—2002年间佛坪大熊猫的监测数据进行分析, 建立佛坪保护区地理信息系统, 得到大熊猫的分布和密度、以及人类活动干扰分布强度, 该研究为保护区管理者的判断和决策提供了科学而方便的依据。

(2)针对不同的研究构建专门的空间模型。种群与环境是一个复杂的系统, 根据已有知识建立专门的空间模型是个切实有效的办法。例如, 在物种保护方面, 保护生物学家常采用种群生存力分析(PVA)模拟种群动态并建立灭绝概率与种群数量的关系[44]。Stevens et al.将黄条蟾蜍置于适宜的空间环境中, 结合PVA理论方法可以更准确的得到保护区范围[45]。Kostova等为草原田鼠构建了基于个体的空间模型, 考虑了动物个体年龄性别差异、一夫一妻制特点、觅食饥饿造成的个体能量水平差异以及植被因季节气候差异、动物觅食而产生的变化, 来探究栖息地尺寸和种群续存之间的关系[46]。田昊等为大熊猫构建了种群动态膜系统, 以大熊猫谱系数据为基础, 通过个体行为和种群特征分析种群动态中生殖参数在多年内的变化规律[47]。Hammershøj等基于丹麦的真实景观建立基于个体的元胞栅格模型, 考虑养殖场的地理位置、每个养殖场的繁殖数量, 通过模拟貂的逃生、繁殖、死亡、扩散等行为, 来预测貂的空间分布[48]。Stenglein等为苏必利尔湖南部的狼群构建了离散的二维规则格网模型, 根据格网内道路密度和农田比率赋以不同的死亡率, 同时考虑现实空间中水体、保护区、农田等生境因素和狼的生活史特征, 来探究人类活动(道路、农业发展)对种群动态的影响[49]。

此外, 根据研究目标的不同, 可进一步发展出多种空间模拟模型。针对种群生态学家关注的热点问题, 可以分别构建空间分布模型、空间扩散模型、空间相互作用模型、空间竞争模拟模型等等。

(3)种群动态模拟模型具备了向综合生态过程模拟发展的条件。综合生态过程模型的实现需要生态学机制和计算机技术的两方面的支持。在生态学机制方面, 过去的种群动态研究已经获得的丰富的成果, 揭示了物种行为特征、生活史及种间关系等因素对种群动态的影响。在计算机技术方面, GIS帮助实现了水文和大气过程模拟。分布式水文模型将气候和下垫面因子的空间异质性纳入考虑, 从时空尺度模拟水文过程, 使水文物理过程越来越接近现实世界[50-51]。大气环境模拟在处理紧急污染事件中发挥了重要作用, 模型的现实性显著影响到模拟效果[52-53]。综合生态过程模拟可以采用多样的方法实现, 如元胞自动机[54]、粒子群算法[55]等。多种多样的地表过程模拟方法, 为刻画复杂的生态环境提供了有力工具, 为种群动态时空模型的发展奠定了基础。

构建种群时空动态模型, 对模拟结果进行分析与表达, 包括对种群数量特征、年龄结构、死亡来源等时间动态的分析表达, 以及意外死亡率分布、生境适宜性分布、种群密度、种群空间模式等空间特征的分析表达。在GIS矢量、栅格两种空间数据结构下, 实现包括模型输入, 环境主体、斑块主体、动物个体、动物种群等模型主体的初始化; 实现动物个体运动、食草动物个体进食、食肉动物个体捕食、动物个体繁殖、动物个体年龄增长、动物个体死亡、斑块主体能量恢复、意外死亡率空间化、斑块适宜性计算等子模型。在GIS的支持下, 实现结合了动物活动和环境变化的综合生态过程模型已经成为可能。

综合生态过程模型是最复杂的种群动态模型, 在未来的种群动态研究中具有重要意义。一方面它可应用于种群发展或绝灭的机制; 另一方面应用于实际问题, 为保护动物提供科学依据。

4 结语

本文回顾了种群动态模型的产生和发展过程, 根据模型的形式和功能, 将已有模型分为了数学模型和空间模型两类。数学模型注重种群数量变化, 而空间模型具有较强的种群时空分布动态模拟能力。本文分别介绍了“J”型增长模型、“S”型增长模型、Lotka-Voltera模型等数学模型和异质种群模型、空间精确性种群模型和基于个体的种群模型等空间模型。数量模型是帮助生态学家了解动物生活史和种群数量变化关系的有力工具; 空间模型则为学者研究更复杂的种群动态问题提供支持。种群动态模型从出现以来,经历了融合与发展,对种群动态研究产生了重要影响。本文认为与GIS结合将有助于种群动态模型的进一步发展, 并展望了种群动态模拟的几个发展方向。

[1] 孙儒泳. 种群的科学管理与数学模型[M]. 上海: 上海科学技术出版社, 1985.

[2] 邬建国. 数学模型与自然保护科学[J]. 应用生态学报, 1992, 3(3): 286–288.

[3] 马世骏. 昆虫种群的空间、数量、时间结构及其动态[J]. 昆虫学报, 1964, 13(1): 38–55.

[4] 刘利民, 吴素文.生态学中的数学模型[J]. 沈阳农业大学学报, 2000, 31(3): 295-299.

[5] 马尔萨斯. 人口原理[M]. 王惠惠, 译.西安: 陕西师范大学出版社. 2008.

[6] MINAR J, VERHULST P. The discoverer of the logistic curve[J]. Human Biology, 1933, 5(4): 673–689.

[7] PEARL R, REED L. On the rate of growth of the population of the United States since 1790 and its mathematical representation[J]. Proceedings of the National Academy of Sciences of the United States of America, 1920, 6(6): 275–288.

[8] REED L, PEARL R. On the summation of logistic curves[J]. Journal of the Royal Statistical Society, 1927, 90(4): 729–746.

[9] MONK A, JETER H. The Logistic Curve and the Prediction of the Population of the Chicago Region[J]. Journal of the American Statistical Association, 1928, 23(164): 361–385.

[10] FISHER R. THE WAVE OF ADVANCE OF ADVAN­TAGEOUS GENES[J]. Annals of Human Genetics, 1937, 7(4): 355–369.

[11] 刘汉武. 两性具有不同出生率和死亡率的种群动态[J]. 生态学杂志, 2003, 22(1): 63–65.

[12] 刘汉武, 王荣欣, 刘建新. 具有性别结构的食饵-捕食者模型[J]. 生物数学学报, 2005, 20(2): 179–182.

[13] 邬建国. Metapopulation(复合种群)究竟是什么?[J]. 植物生态学报, 2000, 24(1): 123–126.

[14] HANSKI I, GILPIN M. Metapopulation dynamics: brief history and conceptual domain[J]. Metapopulation Dyna­mics Empirical & Theoretical Investigations, 1991, 42(1/2): 3–16.

[15] HANSKI I, KUUSSAARI M, NIEMINEN M. Metapo­pulation Structure and Migration in the Butterfly Melitaea Cinxia[J]. Ecology, 1994, 75(3): 747–762.

[16] MARSH D, TRENHAM P. Metapopulation Dynamics and Amphibian Conservation[J]. Conservation Biology, 2010, 15(1): 40–49.

[17] VERBOOM J, SCHOTMAN A, OPDAM P. European Nuthatch Metapopulations in a Fragmented Agricultural Landscape[J]. Oikos, 1991, 61(2): 149–156.

[18] BREWSTER C, ALLEN J, KOPP D. IPM from Space: Using Satellite Imagery to Construct Regional Crop Maps for Studying Crop-Insect Interaction[J]. American Entomolo­gist, 1999, 45(2): 105–117.

[19] PULLIAM H, DUNNING J. Spatially Explicit Population Models[J]. Ecological Applications, 1995, 5(1): 2.

[20] DUNNING J, STEWART D, DANIELSON B, et al. Spatially explicit population models: current forms and future uses[J]. Ecological Applications, 1995, 5(1): 3–11.

[21] MOEN R, PASTOR J, COHEN Y. A SPATIALLY EXPLICIT MODEL OF MOOSE FORAGINGAND ENER­GETICS[J]. Ecology, 1997, 78(2): 505–521.

[22] WIEGAND T. Expansion of Brown Bears () into the Eastern Alps: A Spatially Explicit Population Model[J]. Biodiversity & Conservation, 2004, 13(1): 79– 114.

[23] PITT J, WOMER S, SUAREZ A. Predicting Argentine ant spread over the heterogeneous landscape using a spatially explicit stochastic model[J]. Ecological Applications, 2009, 19(5): 1176–1186.

[24] 程远峰. 野猪种群动态影响模拟预警系统的构建与研究[D]. 哈尔滨: 东北林业大学, 2011.

[25] DEANGELIS D, MOOIJ W. Individual-Based Modeling of Ecological and Evolutionary Processes1[J]. Annual Review of Ecology Evolution & Systematics, 2005(36): 147–168.

[26] MADENJIAN C, JOHNSON B, CARPENTER S. Stocking Strategies for Fingerling Walleyes: An Individual-Based Model Approach[J]. Ecological Applications, 1991, 1(3): 280–288.

[27] FAHRIG L. How much habitat is enough?[J]. Biological Conservation, 2001, 100(1): 65–74.

[28] SOUTH A, KENWARD R. Mate Finding, Dispersal Distances and Population Growth in Invading Species: A Spatially Explicit Model[J]. Oikos, 2001, 95(1): 53–58.

[29] LETCHER B. An individual-based, spatially-explicit simulation model of the population dynamics of the endan­gered red-cockaded woodpecker,[J]. Biological Conservation, 1998, 86(1): 1–14.

[30] 陈求稳, 程仲尼, 蔡德所, 等. 基于个体模型模拟的鱼类对上游水库运行的生态响应分析[J]. 水利学报, 2009, 40(8): 897–903.

[31] 李国庆, 刘长成, 刘玉国, 等. 物种分布模型理论研究进展[J]. 生态学报, 2013, 33(16): 4827–4835.

[32] BUSBY J. BIOCLIM: a bioclimate analysis and prediction system[J]. Plant Protection Quarterly, 1991, 6(1): 8–9.

[33] PHILLIPS S, SCHAPIRE R. A maximum entropy approach to species distribution modeling[C]// International Conference on Machine Learning, ACM, 2004.

[34] 许仲林, 彭焕华, 彭守璋. 物种分布模型的发展及评价方法[J]. 生态学报, 2015, 35(2): 557–567.

[35] 宓春荣, 郭玉民, HUETTMANN F, 等.基于物种分布模型的精确采样提高目标物种发现率——以黑颈鹤(), 白头鹤()为例[J]. 生态学报, 2017, 37(13): 4476–4482.

[36] 翟天庆, 李欣海.用组合模型综合比较的方法分析气候变化对朱鹮潜在生境的影响[J]. 生态学报, 2012, 32(8): 2361–2370.

[37] HOUGHTON J. Climate change 2001: the scientific basis[J]. Netherlands Journal of Geosciences, 2001, 87(3): 197–199.

[38] 沈涛, 张霁, 申仕康, 等. 西南地区红花龙胆分布格局模拟与气候变化影响评价[J]. 应用生态学报, 2017, 28(8): 2499–2508.

[39] STEARNS S. Life-history tactics: a review of the ideas[J]. Quarterly Review of Biology, 1976, 51(1): 3.

[40] DASZAK P, CUNNINGHAM A, HYATT A. Emerging infectious diseases of wildlife-threats to biodiversity and human health[J]. Science, 2000, 287(5452): 443–9.

[41] EASTERLING D. Climate Extremes: Observations, Modeling, and Impacts[J]. Science, 2000, 289(5487): 2068–2074.

[42] 韦月鸾, 谭卫宁, 莫健清, 等. GIS技术在木论自然保护区白鹇种群动态监测中的应用[J]. 广西林业科学, 2012, 41(3): 282–285.

[43] 赵德怀, 叶新平, 雍严格, 等. GIS在野生大熊猫种群监测分析中的应用[J]. 陕西师范大学学报(自然科学版), 2006, 34(S1): 168–173.

[44] 田瑜, 邬建国, 寇晓军, 等.种群生存力分析(PVA)的方法与应用[J]. 应用生态学报, 2011, 22(1): 257–267.

[45] STEVENS V, BAGUETTE M. Importance of Habitat Quality and Landscape Connectivity for the Persistence of Endangered Natterjack Toads[J]. Conservation Biology, 2008, 22(5): 1194–1204.

[46] KOSTOVA T, CARLSEN T, KERCHER J. Individual- based spatially-explicit model of an herbivore and its resource: the effect of habitat reduction and fragmen­tation[J]. Comptes Rendus Biologies, 2004, 327(3): 261– 276.

[47] 田昊, 张葛祥, 荣海娜, 等. .基于种群动态膜系统的大熊猫种群模型[J]. 计算机应用, 2018(05): 1488–1493+149.

[48] HAMMERSHOJ M, TRAVIS J, STEPHENSON C. Incorporating evolutionary processes into a spatially- explicit model: exploring the consequences of mink-farm closures in Denmark[J]. Ecography, 2006, 29(4): 465–476.

[49] STENGLEIN J, GILBERT J, WVDEVEN A, et al. An individual-based model for southern Lake Superior wolves: A tool to explore the effect of human-caused mortality on a landscape of risk[J]. Ecological Modelling, 2015(302): 13–24.

[50] 王中根, 刘昌明, 吴险峰. 基于DEM的分布式水文模型研究综述[J]. 自然资源学报, 2003, 22(2): 168–173.

[51] 江净超, 朱阿兴, 秦承志, 等. 分布式水文模型软件系统研究综述[J]. 地理科学进展, 2014, 33(8): 1090–1100.

[52] 张攀攀, 王义祥, 邬群勇, 等. GIS与大气环境模型的集成及其应用[J]. 环境科学研究, 2010, 23(5): 575–580.

[53] 郭东恩, 沈燕, 张峰. GIS技术在大气环境模拟与评价系统中的应用探讨[J]. 测绘科学, 2011, 36(5): 100–102.

[54] ARGOLO C, BARROS P, TOME T, et al. Threshold of coexistence and critical behavior of a predator-prey stochastic model in a fractal landscape[J]. Journal of Statistical Mechanics Theory & Experiment, 2016(8): 083204.

[55] KENNEDY J, MENDES R. Population structure and particle swarm performance[C]// Congress on Evolutionary Computation, IEEE, 2002.

Animals population dynamic models: a review and outlook

Xi Changbai1,2, Chi Yao1,2, QIAN Tianlu1,2, SHeng Caiying1,2, WANG Jiechen1,2,3,*

1. School of Geography and Ocean Science, Nanjing University, Nanjing 210023, China 2. Jiangsu Provincial Key Laboratory of Geographic Information Science and Technology, Nanjing 210023, China; 3. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China

Being developed through over one hundred years, there has been much progress in the field of the population dynamic model. In this paper, a review of its achievements was given as well as a looking forward to its future developments. Population dynamic includes quantitative dynamic and spatial-temporal distribution dynamic. According to the form and research content, the population dynamic models can be divided into mathematic models and spatial models. The mathematic models simulate the population fluctuations by mathematical equations, such as “J” growth model, “S” growth model and Lotka-Voltera model, etc. Spatial models focus on spatial pattern of population and habitat, such as Metapopulation Model, Spatially Explicit Population Model and Individual-Based Models. Population dynamic models have been successfully applied in species protection, climate change and land management. Presently population dynamic models are short in spatial information expression, and it is considered that combining with geographic information technology is the trend of population dynamic model.

Geographic Information System; population dynamic; spatial model; Species Distribution Model; animal protection

10.14108/j.cnki.1008-8873.2019.02.030

Q149

A

1008-8873(2019)02-225-08

2018-03-12;

2018-04-10

国家自然科学基金项目(41871294)

席唱白(1994—) , 男, 博士研究生, 研究方向为地图学与GIS, E-mail: xicb11@smail.nju.edu.cn

王结臣(1973—), 男, 博士, 教授, 研究方向为地图学与GIS, E-mail: wangjiechen@nju.edu.cn

席唱白, 迟瑶, 钱天陆, 等. 动物种群动态模型研究的进展与展望[J]. 生态科学, 2019, 38(2): 225-232.

Xi Changbai, Chi Yao, QIAN Tianlu, et al. Animals population dynamic models: a review and outlook[J]. Ecological Science, 2019, 38(2): 225-232.