W-Cu共掺杂ZnO电子结构和光学性质

方文玉, 王晓雯, 高 深

(1. 湖北医药学院公共卫生与管理学院, 十堰442000； 2. 湖北医药学院基础医学院, 十堰442000； 3. 武汉大学电气工程学院, 武汉430072)

1 引 言

ZnO是一种新型的直接带隙宽禁带化合物半导体材料, 在室温下其禁带宽度为3. 37 eV, 激子束缚能是60 meV[1], 在光探测器、电致荧光器件、导电薄膜材料等领域有着广泛的应用. ZnO具有较好的化学稳定性和热稳定性, 容易掺杂其他元素而形成性能更为优良的材料. 黄云霞等人[2]通过固相反应法制备Al掺杂ZnO粉末, 发现其介电函数呈增大趋势. 丁国静等人[3]通过水热法制备了Al3+掺杂ZnO纳米棒, 发现能够显著提高ZnO的传导电子的能力, 光电转化效率也显著提升. Ca掺杂ZnO能够提高其电导率, 具有较高的Seebeck系数和综合电性能[4]. 胡志刚等人[5]发现, Fe、Ni单掺杂和共掺杂ZnO的吸收光谱均发生明显的红移, 并都在1.3 eV处出现较强的吸收峰. 与此同时, 刘小村等人[6]通过计算In掺杂ZnO电子结构发现, 随着In掺杂浓度增加, ZnO的晶格常数也变大, 其带隙变窄. 另外, Mn掺杂ZnO薄膜引起光学及磁性的变化也引起了人们广泛兴趣[7]. 目前, 也有相关文献报道, Cu和W单掺杂能够改变ZnO光电性质[8-12], 适合制备各种性能的光电子器件.

综上所述, 实验上Cu和W单掺杂ZnO已经进行了研究, 理论上的也有一定的报道, 但是对W-Cu共掺杂协同效应的本质还有有待进一步研究. 目前, 从理论上对W-Cu共掺杂ZnO的光电性质计算分析尚未见报道. 因此, 本文采用基于密度泛函理论的第一性原理计算研究了W掺杂、Cu掺杂、W-Cu共掺杂ZnO物理性质, 并对结果进行了分析与探讨, 为相关实验研究提供了方向.

2 模型与方法

2.1 结构模型

本文选取的ZnO是比较稳定的六方纤维矿结构, 空间群是P63mc, 晶胞由Zn和O的六角密堆积在c轴方向上反向嵌套而成. 本征ZnO晶格常数为a=b=3. 24927 Å,c=5. 20544 Å,α=β=90°,γ=120°. 研究所用的晶胞是基于ZnO原胞建立的2×2×2超晶胞, 掺杂时分别用W、Cu原子替代Zn原子, 替代位置如图1所示, W、Cu单掺杂及共掺杂分别记为Zn16O16、Zn15W1O16、Zn15Cu1O16、Zn14W1Cu1O16.

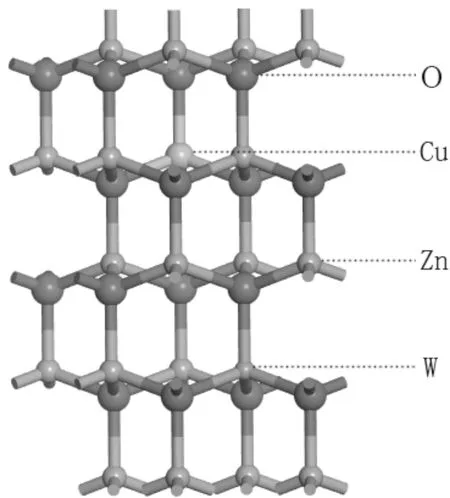
图 1 W-Cu共掺杂ZnO(2×2×2)超晶胞模型Fig.1 Model of W-Cu codoped ZnO supercell

2.2 计算方法

本文计算主要是由CASTEP软件来完成的计算中采用周期性边界条件, 运用广义梯度近似GGA的PBE算方法来处理电子相互间的交换关联能. 选取Zn、O、W、Cu的价电子组态分别为3d104s2、2s22p4、5s25p65d46s2、3d104s1. 计算时选取的平面波截断能是Ecut=400 eV, 布里渊区积分采用4×4×2Monkhorst-Pack特殊K点对全布里渊区求和, 计算均在倒格矢中进行. 在自洽场计算中, 能量的收敛精度为1. 0×10-5eV·atom-1, 每个原子上的受力不大于0. 03 eV·nm-1, 内应力收敛精度0. 05 GPa, 原子最大位移收敛标准1. 0×10-3nm, 计算各种体系时均进行结构优化.

3 结果与讨论

3.1 晶体结构及稳定性分析

几何结构优化的超晶胞参数列于表1, 可以看出优化后的ZnO晶格常数a=b=6.594 Å,c=10.602 Å, 这与实验值[13](a=b=0.65 Å,c=10.41 Å)十分接近, 说明计算方法是合理的. 当W掺杂ZnO时, W离子半径(0. 062 nm)较Zn离子半径(0. 074 nm)稍小, 按照量子化学理论, 当W取代Zn时, 其晶胞也应该减小. 但计算的结果显示, 掺杂后的晶格常数相对于本征ZnO均有不同程度增大, 晶胞的体积也变大, 这与实验结果是一致的[12]. 这是因为W离子对Zn离子的代替, W离子多余电荷之间相互排斥作用增强, 体系能量的增高导致体积变大. Cu离子半径(0. 072 nm)较较Zn离子半径略小, Cu和Zn是同周期的相邻元素, 当Zn被Cu替换后, 离子间电荷分布差异性较小, 因而对晶胞的影响较小, 因此Cu单掺杂ZnO后晶胞体积稍微变小.

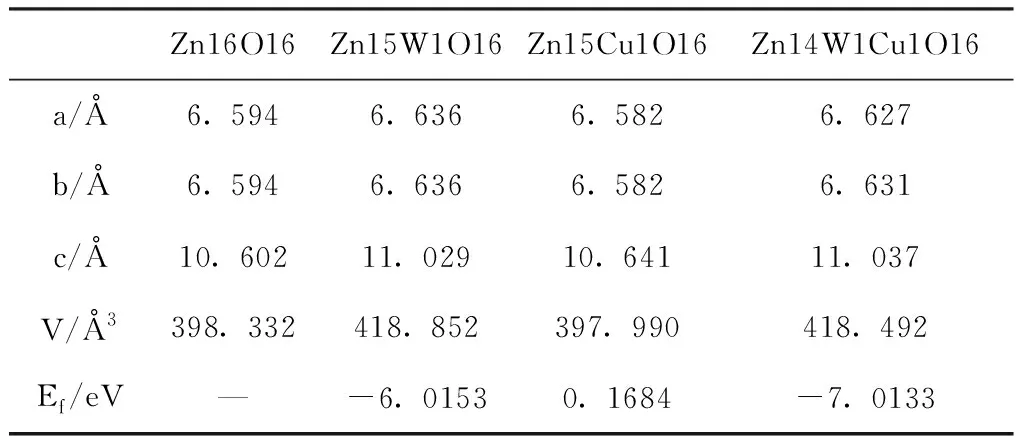
表1 优化后的超晶胞参数和结合能

为了分析掺杂体系的稳定性, 我们引入结合能Ef的概念. 杂质结合能是分析原子掺杂难易程度的物理量, 电子在非自旋极化条件下, 掺杂结合能的表达式[14]:

Ef=Ed-EZnO-Ex+EZn

(1)

其中,Ef表示掺杂体系结合能,Ed表示掺杂后体系的总能量,EZnO表示本征ZnO总能量,Ex和EZn分别表示单个掺杂原子和Zn原子的能量. 从表1可以看出, Cu单掺杂的结合能最大, 最不容易掺杂；而W、Cu共掺杂的结合能最低, 最容易掺杂, 掺杂后的ZnO最稳定.

3.2 能带结构和态密度分析

图2是W、Cu单掺杂及共掺杂ZnO能带图, 这里选取费米能级附近(-4—4 eV)的能带图. 从图2(a)可以看出, 本征ZnO的导带底及价带顶都在G点, 说明ZnO为直接带隙半导体, 其禁带宽度Eg=0.729 eV. 结果与文献[4-7]计算的结果基本一致, 但比实验值(Eg=3.37 eV)明显偏低. 这是因为GGA算法对Zn-3d电子能量被过高估计, 导致它与O-2p电子间相互作用增强, 导致价带宽度变大, 因而计算的带隙偏低, 但是这并不影响对ZnO光电性质的分析. 当W掺杂ZnO时, 价带和导带均不同程度下移, 费米能级远离价带, 靠近导带, 属于n型掺杂. 而Cu单掺杂时, 价带和导带均往费米能级靠近, 带隙展宽, 并在禁带中出现杂质能级且相对靠下, 属于p型掺杂. W-Cu共掺杂时, 部分杂质能级与导带相连, 费米能级附近的能带结构更加丰富, 说明导带低附近的量子态基本上已被电子填满, 半导体发生简并并呈现金属特性.

图3是单掺杂及共掺杂ZnO态密度, 这里选取-20-10 eV区间, 由于W-s态在该区间几乎为零, 图中没有标注. 从图3(a)可以看出, 本征ZnO导带主要由Zn-4s态和O-2p电子态组成, 价带则是由Zn-3d态和O-2p态杂化形成. W掺杂和W-Cu共掺杂时, 态密度向低能方向移动. Cu单掺杂时, 总态密度相对本征ZnO变化很小, 通过观察分态密度发现, 其价带主要由Cu-3d、O-2p和Zn-3d共同组成, 增加了价带的态密度, 另一部分Cu-3d态电子在禁带中形成杂质能级, 有助于电子从价带到导带的跃迁, 增加了ZnO的电导率.

3.3 光学性质

介电函数是研究光学性质的常用指标, 固体的宏观光学性质可以通过复介电函数来表述:

ε(ω)=ε1(ω)+ε2(ω)

(2)

其中,ω为频率,ε1(ω)和ε2(ω)分别表示介电函数的实部和虚部, 虚部ε2(ω)是与光学吸收直接相关的, 实部ε1(ω)可以通过Kramers-Krönig关系计算得到, 吸收系数及反射率则可以通过ε1(ω)和ε2(ω)给出[7]:

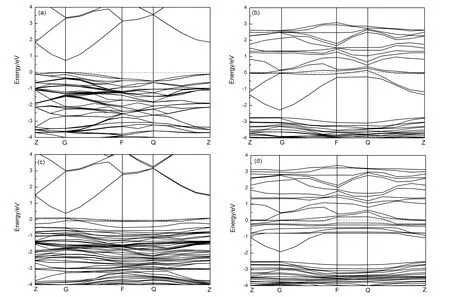
图 2 单掺杂及共掺杂ZnO能带图 (a)本征ZnO；(b)W掺杂；(c)Cu掺杂；(d)W-Cu共掺杂Fig.2 The band structures of (a)pure ZnO;(b)W doped ZnO;(c)Cu doped ZnO;(d)W, Cu codoped ZnO

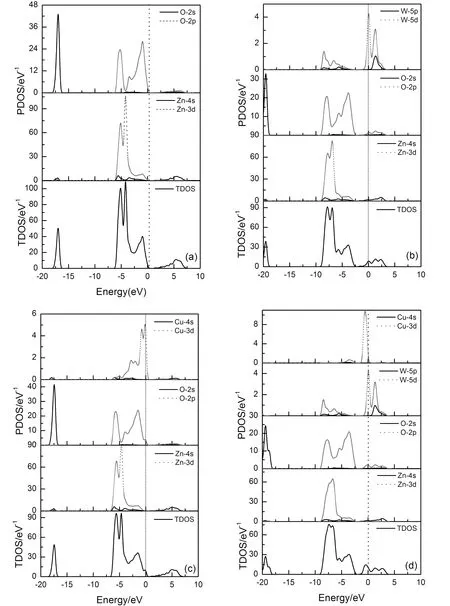
图 3 单掺杂及共掺杂ZnO态密度 (a)本征ZnO；(b)W掺杂；(c)Cu掺杂；(d)W-Cu共掺杂Fig. 3 The DOS of (a)pure ZnO;(b)W doped ZnO;(c)Cu doped ZnO;(d)W, Cu codoped ZnO

(3)

因GGA算法导致计算能隙偏小, 所以在计算光学性质时用剪刀算符对能隙进行修正, 这里剪刀算符取值为2. 641 eV(实验值3.37 eV—计算值0.729 eV), 入射光的极化方向为<100>垂直照射.

图4是单掺杂及共掺杂ZnO的介电函数虚部, 从中可以看出, 掺杂后ZnO的介电函数相对本征ZnO其变化主要表现在低能量的区域, 在4.4 eV后几乎没有太大变化, 说明掺杂后光学性质的变化主要低能量区域. 本征ZnO在4.4, 9.0和12.9 eV处有三个峰值, 这与何静芳等人[15]计算结果(4.3, 9.0, 12.9 eV)基本一致. 掺杂后, 介电函数在4.4 eV的峰值消失, 在3.5 eV附近出现一个明显的峰值, 这是由价带顶的O-2p态电子向掺杂原子电子态(W-5d和Cu-3d态电子)的跃迁产生的. 值得注意的是, 在0-4 eV范围内, W单掺杂和W-Cu共掺杂ZnO的介电函数虚部相似, 说明在这个区域, 二者的光学性质相似.

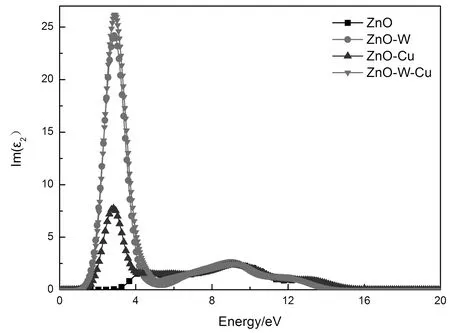
图 4 单掺杂及共掺杂ZnO的介电函数虚部Fig.4 Imaginary part of dielectric function of pure and doped ZnO

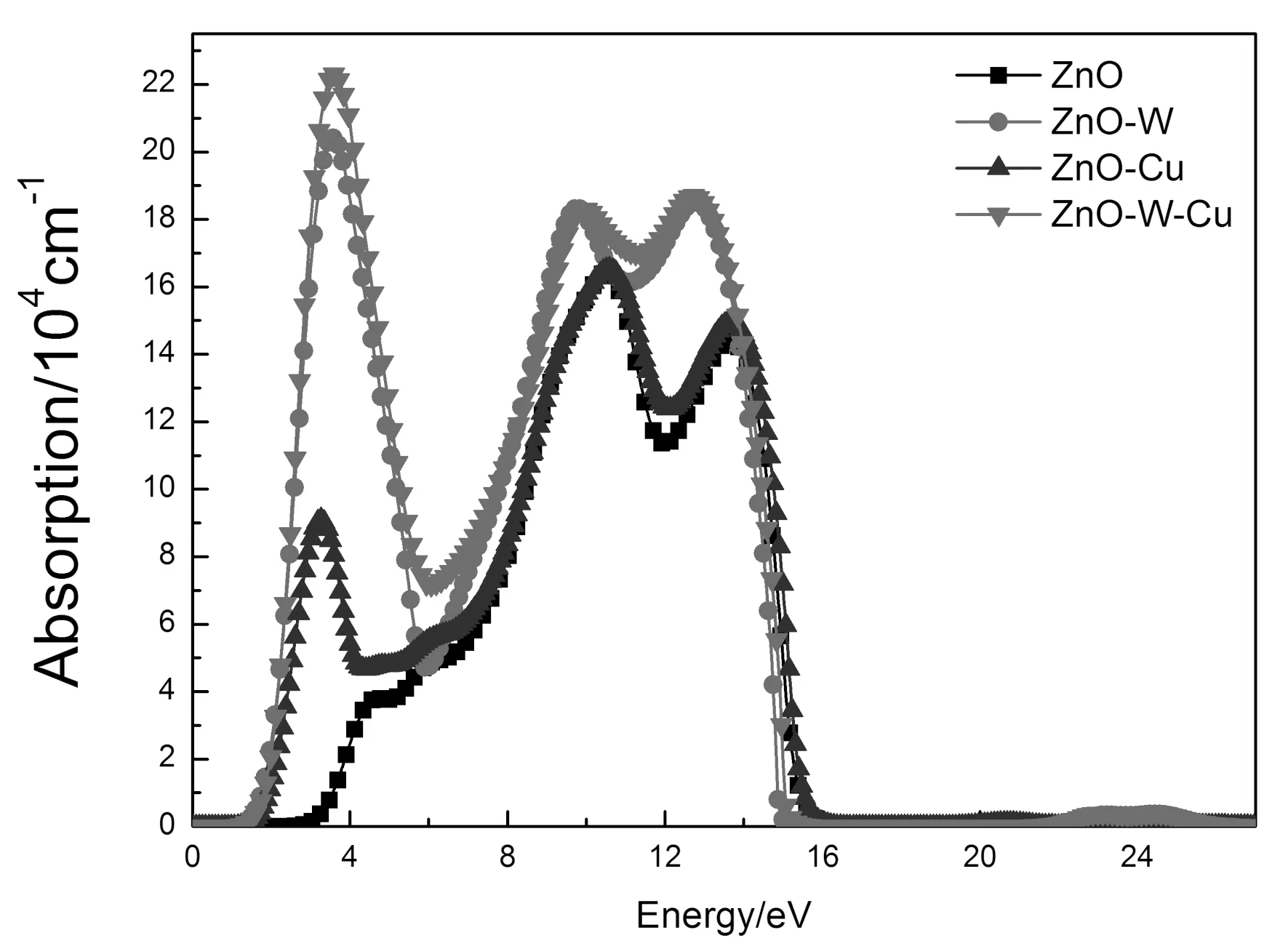
图 5 单掺杂及共掺杂ZnO的吸收系数Fig.5 Absorption spectra of pure and doped ZnO

图5是本征ZnO和各掺杂体系的吸收系数, 可以看出, 掺杂后的吸收系数向低能方向移动, 这主要是因为掺杂后, 在价带顶部会存在空穴, 电子的带内跃迁产生光吸收. 观察本征ZnO的吸收边发现, 其吸收边能量在3.4 eV附近, 这符合吸收边大于能隙的规则, 即3.4 eV>3.37 eV. 比较三种掺杂情况下的ZnO可以看出, 掺杂后的吸收系数在2.0-4.0 eV范围内显著增大, 尤其是W单掺杂和W-Cu共掺杂, 在这一范围内吸收效果非常接近, W-Cu共掺杂的吸收峰值稍高于W单掺杂, 考虑到共掺杂的结合能最低, 因此它更适合用来制备太阳光谱吸收材料.

图6是掺杂前后的反射率, 可以发现, 掺杂后的反射率比掺杂前都要大, 尤其是在4 eV和15 eV两个峰值附近, W掺杂和W-Cu共掺杂反射率增大最为显著, 通过图5可以发现, 在这两个峰值附近的吸收系数也明显增大. 根据能量守恒定律, 光照射物体时, 能量分为三个部分: 吸收光、反射光和透射光, 因此W掺杂和W-Cu共掺杂对4 eV和15 eV附近的光子具有较小的透射率, 适合用于制备特定光学器件.

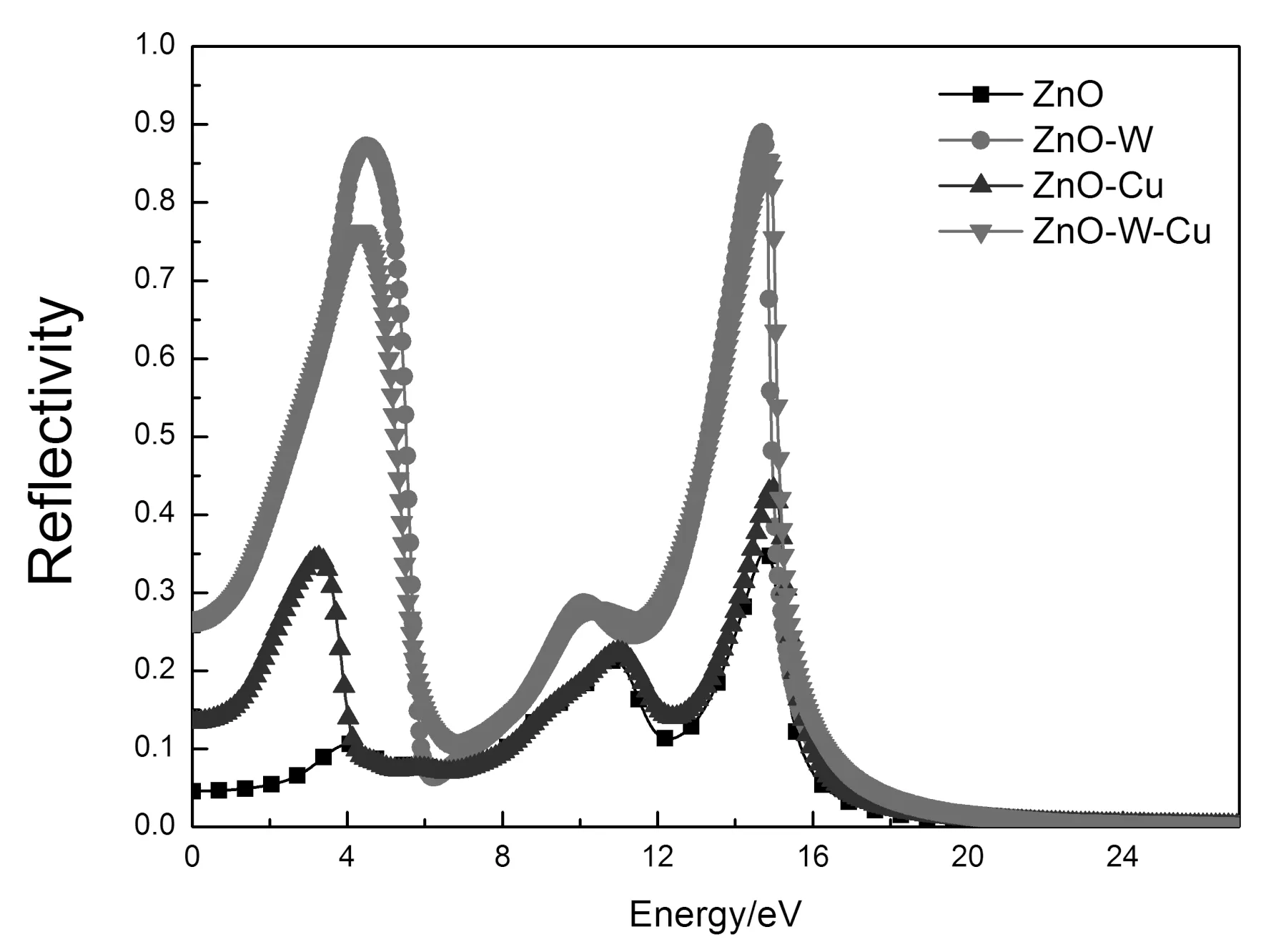
图 6 单掺杂及共掺杂ZnO的反射率Fig.6 Reflectivity spectra of pure and doped ZnO

4 结 论

本文利用密度泛函理论采用第一性原理平面波超软赝势方法, 计算了本征ZnO, W、Cu单掺杂及W-Cu共掺杂ZnO电子结构及光学性质. 计算结构表明, W单掺杂时增加了杂质能带电子浓度, 属于n型掺杂, 而Cu掺杂时则增加空穴浓度, 属于p型掺杂, W-Cu共掺杂时, 杂质能级与导带相连, 半导体出现简并状态, 呈现金属特性. 三种掺杂情况下, ZnO的光谱吸收边均发生红移, 对太阳光谱的吸收效果增强, 对比发现W-Cu共掺杂更适合用于制备太阳能吸收材料. 掺杂后, ZnO反射率出现2个高峰值, 根据能量守恒定律, W单掺杂和W-Cu共掺杂ZnO对4 eV和15 eV附近的光子具有较小的透射率.